手把手教你写CS231N作业一 KNN分类器 详细解析 作业源文件 数据集

一些准备工作

• python环境
• 官方课程给出的源文件在这里

根据文件里的指导一步步编写答案就可。第一个实现KNN分类器。

• 如果是windows环境，需要首先下载数据集。The CIFAR-10 dataset官网
  官网上也有关于本数据集的说明
  往下翻到下载，选择python版本的下载即可。如果用的是Unix系统可以用斯坦福课程给出的方式进行数据集的获取。

inline question的分析

//to do

knn.ipynb

首先打开spring1819_assignment1\assignment1文件夹下面的knn.ipynb。
我是用的anaconda 用jupyter notebook打开这个文件。

from spring1819_assignment1.k_nearest_neighbor import KNearestNeighbor

KNearestNeighbor是要我们自己写的一个类，在spring1819_assignment1\assignment1\cs231n\classifiers里的k_nearest_neighbor.py文件中。
第一次做作业可以先用别的写的k_nearest_neighbor.py运行一遍knn.ipynb，然后再自己写这个分类器。
先试试这个自定义的类能不能导入，我在__init__函数里加了一个打印语句。

knn=KNearestNeighbor()

This is KNN2 classifier by wzd

import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# coding:utf-8

导入数据，课程示例给出的方法不适合Windows系统，需要手动下载数据集，然后用绝对路径加载

cifar10_dir = 'D:\CIFAR10'#data_path
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)

training data里有五万个数据，但是本作业只会选取一部分使用

print ('Training data shape: ', X_train.shape)
print ('Training labels shape: ', y_train.shape)
print ('Test data shape: ', X_test.shape)
print ('Test labels shape: ', y_test.shape)

Training data shape:  (50000, 32, 32, 3)
Training labels shape:  (50000,)
Test data shape:  (10000, 32, 32, 3)
Test labels shape:  (10000,)

把数据集里的例子可视化，展示一些训练集里面的样本样本

classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):
    idxs = np.flatnonzero(y_train == y)
    idxs = np.random.choice(idxs, samples_per_class, replace=False)
    for i, idx in enumerate(idxs):
        plt_idx = i * num_classes + y + 1
        plt.subplot(samples_per_class, num_classes, plt_idx)
        plt.imshow(X_train[idx].astype('uint8'))
        plt.axis('off')
        if i == 0:
            plt.title(cls)
plt.show()

在本练习中，为了更有效地执行代码，对数据进行了细分

num_training = 5000
mask = list(range(num_training)) #机产生训练样本的位置
X_train = X_train[mask] #选择训练样本
y_train = y_train[mask]  #确定训练样本标签

num_test = 500
mask = list(range(num_test))
X_test = X_test[mask]
y_test = y_test[mask]

这里是把(50000, 32, 32, 3)变成 (5000, 3072)。一个图片用一个32323的一行来表示，相当于把一个图片拉成一个行向量。

# Reshape the image data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
print(X_train.shape, X_test.shape)

(5000, 3072) (500, 3072)

用KNN分类器进行训练

classifier = KNearestNeighbor()
classifier.train(X_train, y_train)

This is KNN2 classifier by wzd

KNN分类器是要把预测的样本与训练集比较，找到离训练集最近的。所以train（）的作用是把训练集X_train绑定到类KNearestNeighbor的属性self.X_train

dists = classifier.compute_distances_two_loops(X_test)
print(dists.shape)

(500, 5000)

dists 表示的是test集与training data的距离，dists[i, j] 表示的是test的第i个与training data的第j个的距离。

# We can visualize the distance matrix: each row is a single test example and
# its distances to training examples
plt.imshow(dists, interpolation='none')
plt.show()

这里有问题要回答，关于这个图的理解

得到了dists以后，就可以预测test data里的图片的分类。dists的第i行表示，test的第i个样本与5000个训练集数据的距离，找到距离最小的K个训练集图片，他们的图片类型就是我们预测的结果y_test_pred。
这里指定了k=1，在classifier.predict_labels函数中就只会找到距离最小的一个图片，他的类别就是对test预测的类别。

# Now implement the function predict_labels and run the code below:
# We use k = 1 (which is Nearest Neighbor).
y_test_pred = classifier.predict_labels(dists, k=1)

# Compute and print the fraction of correctly predicted examples
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))

Got 137 / 500 correct => accuracy: 0.274000

在K=1是预测的结果是0.274000

y_test_pred = classifier.predict_labels(dists, k=5)
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))

Got 139 / 500 correct => accuracy: 0.278000

K=5预测的结果是0.278000

y_test_pred = classifier.predict_labels(dists, k=10)
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))

Got 141 / 500 correct => accuracy: 0.282000

K=10预测的结果是0.282000。这也是最好的预测结果，在后面会证明，K=10时是这个超参数最好的取值

# Now lets speed up distance matrix computation by using partial vectorization
# with one loop. Implement the function compute_distances_one_loop and run the
# code below:
dists_one = classifier.compute_distances_one_loop(X_test)

# To ensure that our vectorized implementation is correct, we make sure that it
# agrees with the naive implementation. There are many ways to decide whether
# two matrices are similar; one of the simplest is the Frobenius norm. In case
# you haven't seen it before, the Frobenius norm of two matrices is the square
# root of the squared sum of differences of all elements; in other words, reshape
# the matrices into vectors and compute the Euclidean distance between them.
difference = np.linalg.norm(dists - dists_one, ord='fro')
print('One loop difference was: %f' % (difference, ))
if difference < 0.001:
    print('Good! The distance matrices are the same')
else:
    print('Uh-oh! The distance matrices are different')

One loop difference was: 0.000000
Good! The distance matrices are the same

在分类器中一共用了3中方法来计算dists矩阵，这里是为了验证他们的计算结果是否是相同的。np.linalg.norm是一个计算距离的函数，linalg=linear（线性）+algebra（代数），norm则表示范数。更多关于这个函数的使用参见文档

# Now implement the fully vectorized version inside compute_distances_no_loops
# and run the code
dists_two = classifier.compute_distances_no_loops(X_test)

# check that the distance matrix agrees with the one we computed before:
difference = np.linalg.norm(dists - dists_two, ord='fro')
print('No loop difference was: %f' % (difference, ))
if difference < 0.001:
    print('Good! The distance matrices are the same')
else:
    print('Uh-oh! The distance matrices are different')

No loop difference was: 0.000000
Good! The distance matrices are the same

然后比较三种计算距离矩阵dists的方法，差距还是挺大的。

# Let's compare how fast the implementations are
def time_function(f, *args):
    """
    Call a function f with args and return the time (in seconds) that it took to execute.
    """
    import time
    tic = time.time()
    f(*args)
    toc = time.time()
    return toc - tic

two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
print('Two loop version took %f seconds' % two_loop_time)

one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
print('One loop version took %f seconds' % one_loop_time)

no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
print('No loop version took %f seconds' % no_loop_time)

# You should see significantly faster performance with the fully vectorized implementation!

# NOTE: depending on what machine you're using, 
# you might not see a speedup when you go from two loops to one loop, 
# and might even see a slow-down.

Two loop version took 68.126827 seconds
One loop version took 148.250298 seconds
No loop version took 0.632674 seconds

Cross-validation

交叉验证主要是验证k值选择哪个更好
交叉验证思路：将训练集拆分为训练组和验证组，来筛选比较好的超参数
这部分需要自己编写交叉验证的代码

num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]

X_train_folds = []
y_train_folds = []
################################################################################
# TODO:                                                                        #
# Split up the training data into folds. After splitting, X_train_folds and    #
# y_train_folds should each be lists of length num_folds, where                #
# y_train_folds[i] is the label vector for the points in X_train_folds[i].     #
# Hint: Look up the numpy array_split function.                                #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

X_train_folds = np.array_split(X_train,num_folds)
y_train_folds=np.array_split(y_train, num_folds)

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}


################################################################################
# TODO:                                                                        #
# Perform k-fold cross validation to find the best value of k. For each        #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times,   #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all     #
# values of k in the k_to_accuracies dictionary.                               #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

for k in k_choices:
    k_to_accuracies[k]=[]
    for i in range(num_folds):
        X_train_cv = np.vstack(X_train_folds[:i] + X_train_folds[i+1:])
        y_train_cv = np.hstack(y_train_folds[:i] + y_train_folds[i+1:])
        X_test_cv = X_train_folds[i]
        y_test_cv = y_train_folds[i]   
        
        classifier=KNearestNeighbor()        
        classifier.train(X_train_cv, y_train_cv)
        dists=classifier.compute_distances_no_loops(X_test_cv)
        y_test_pred = classifier.predict_labels(dists, k)
        num_correct = np.sum(y_test_pred == y_test_cv)
        accuracy = float(num_correct) / X_test_cv.shape[0]
        k_to_accuracies[k].append(accuracy)

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

# Print out the computed accuracies
for k in sorted(k_to_accuracies):
    for accuracy in k_to_accuracies[k]:
        print('k = %d, accuracy = %f' % (k, accuracy))

This is KNN2 classifier by wzd
This is KNN2 classifier by wzd
This is KNN2 classifier by wzd
This is KNN2 classifier by wzd
This is KNN2 classifier by wzd
This is KNN2 classifier by wzd
......
k = 1, accuracy = 0.263000
k = 1, accuracy = 0.257000
k = 1, accuracy = 0.264000
k = 1, accuracy = 0.278000
k = 1, accuracy = 0.266000
k = 3, accuracy = 0.239000
k = 3, accuracy = 0.249000
k = 3, accuracy = 0.240000
k = 3, accuracy = 0.266000
k = 3, accuracy = 0.254000
k = 5, accuracy = 0.248000
......
k = 100, accuracy = 0.263000
k = 100, accuracy = 0.256000
k = 100, accuracy = 0.263000

这部分代码比较复杂。首先是把训练集分为5组，使用array_split即可。###分割结果是一个列表，而不是矩阵。请务必注意列表和矩阵的区别：列表是Python的基本数据类型，而矩阵是NumPy中的数据类型。如果弄混了这一点，后面的程序将会非常难以理解（我就弄混了，所以纠结了很久orz）。接下来，很关键的一点是如何按照5折交叉验证的要求组合训练集。

X_train_cv = np.vstack(X_train_folds[:i] +
X_train_folds[i+1:])这句话是容易产生困扰的。vstack用于在0号轴上连接多个矩阵（请按照前面介绍的规则理解这句话。连接后，0号轴的大小将发生变化，而其它轴的大小不变），函数的参数应当为待连接的矩阵组成的元组（tuple）。而在这行代码中，并没有传入元组，而是传入了两个列表相加的结果。首先，这里是列表相加而不是矩阵相加，Python的加号运算符用于列表时会直接把两个列表连接起来。因此相加的结果是一个长度为4的列表，列表中每个元素都是1000×3072的矩阵。将列表传入vstack后，会自动调用元组的构造函数tuple(list)将其转换为元组。之后，在0号轴上连接这4个矩阵，得到一个4000×3072的矩阵。相同的原理，使用hstack组合训练集标签，这次是在1号轴上连接矩阵。这又是一个很容易出错的地方，因为vstack和hstack会认为输入矩阵的维度至少为2，比如，代码中的y_train其实是一维矩阵，按理说它应该在0号轴上连接。但是这两个函数会把它当做二维矩阵，认为它是1×1000的矩阵，因此必须在1号轴上连接才能得到1×4000的矩阵。

作者：金戈大王 链接：https://www.jianshu.com/p/275eda2294ea 来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

# plot the raw observations
for k in k_choices:
    accuracies = k_to_accuracies[k]
    plt.scatter([k] * len(accuracies), accuracies)
    
# plot the trend line with error bars that correspond to standard deviation
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()

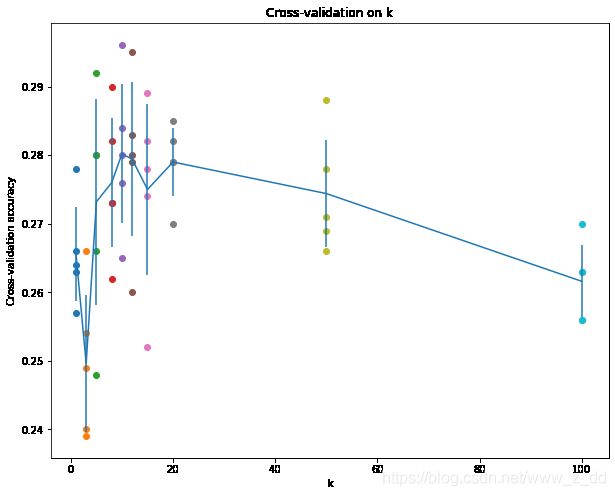
图片k=100时只有三个点，把k_to_accuracies打印出来就可以知道为什么了，因为有两对重复值。

k_to_accuracies

{1: [0.263, 0.257, 0.264, 0.278, 0.266],
 3: [0.239, 0.249, 0.24, 0.266, 0.254],
 5: [0.248, 0.266, 0.28, 0.292, 0.28],
 8: [0.262, 0.282, 0.273, 0.29, 0.273],
 10: [0.265, 0.296, 0.276, 0.284, 0.28],
 12: [0.26, 0.295, 0.279, 0.283, 0.28],
 15: [0.252, 0.289, 0.278, 0.282, 0.274],
 20: [0.27, 0.279, 0.279, 0.282, 0.285],
 50: [0.271, 0.288, 0.278, 0.269, 0.266],
 100: [0.256, 0.27, 0.263, 0.256, 0.263]}

前面把k_to_accuracies计算了出来，k_to_accuracies的每一行都表示k取不同值的计算得出的准确率。

# Based on the cross-validation results above, choose the best value for k,   
# retrain the classifier using all the training data, and test it on the test
# data. You should be able to get above 28% accuracy on the test data.
best_k = 10

classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)

# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))

This is KNN2 classifier by wzd
Got 141 / 500 correct => accuracy: 0.282000

最后用最好的超参数取值k=10来在test data上运行一下。

k_nearest_neighbo.py

KNearestNeighbor类的代码

from builtins import range
from builtins import object
import numpy as np
from past.builtins import xrange


class KNearestNeighbor(object):
    """ a kNN classifier with L2 distance """

    def __init__(self):
        print("This is KNN2 classifier by wzd")

    def train(self, X, y):
        """
        Train the classifier. For k-nearest neighbors this is just
        memorizing the training data.

        Inputs:
        - X: A numpy array of shape (num_train, D) containing the training data
          consisting of num_train samples each of dimension D.
        - y: A numpy array of shape (N,) containing the training labels, where
             y[i] is the label for X[i].
        """
        self.X_train = X
        self.y_train = y

    def predict(self, X, k=1, num_loops=0):
        """
        Predict labels for test data using this classifier.

        Inputs:
        - X: A numpy array of shape (num_test, D) containing test data consisting
             of num_test samples each of dimension D.
        - k: The number of nearest neighbors that vote for the predicted labels.
        - num_loops: Determines which implementation to use to compute distances
          between training points and testing points.

        Returns:
        - y: A numpy array of shape (num_test,) containing predicted labels for the
          test data, where y[i] is the predicted label for the test point X[i].
        """
        if num_loops == 0:
            dists = self.compute_distances_no_loops(X)
        elif num_loops == 1:
            dists = self.compute_distances_one_loop(X)
        elif num_loops == 2:
            dists = self.compute_distances_two_loops(X)
        else:
            raise ValueError('Invalid value %d for num_loops' % num_loops)

        return self.predict_labels(dists, k=k)

    def compute_distances_two_loops(self, X):
        """
        Compute the distance between each test point in X and each training point
        in self.X_train using a nested loop over both the training data and the
        test data.

        Inputs:
        - X: A numpy array of shape (num_test, D) containing test data.

        Returns:
        - dists: A numpy array of shape (num_test, num_train) where dists[i, j]
          is the Euclidean distance between the ith test point and the jth training
          point.
        """
        num_test = X.shape[0]
        num_train = self.X_train.shape[0]
        dists = np.zeros((num_test, num_train))
        for i in range(num_test):
            for j in range(num_train):
                #####################################################################
                # TODO:                                                             #
                # Compute the l2 distance between the ith test point and the jth    #
                # training point, and store the result in dists[i, j]. You should   #
                # not use a loop over dimension, nor use np.linalg.norm().          #
                #####################################################################
                # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

                chazhi=X[i]-self.X_train[j]
                dists[i][j]=np.sqrt((chazhi**2).sum())

                # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        return dists

    def compute_distances_one_loop(self, X):
        """
        Compute the distance between each test point in X and each training point
        in self.X_train using a single loop over the test data.

        Input / Output: Same as compute_distances_two_loops
        """
        num_test = X.shape[0]
        num_train = self.X_train.shape[0]
        dists = np.zeros((num_test, num_train))
        for i in range(num_test):
            #######################################################################
            # TODO:                                                               #
            # Compute the l2 distance between the ith test point and all training #
            # points, and store the result in dists[i, :].                        #
            # Do not use np.linalg.norm().                                        #
            #######################################################################
            # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

            chazhi=X[i]-self.X_train
            dists[i,:]=np.sqrt((chazhi**2).sum(axis=1))

            # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        return dists

    def compute_distances_no_loops(self, X):
        """
        Compute the distance between each test point in X and each training point
        in self.X_train using no explicit loops.

        Input / Output: Same as compute_distances_two_loops
        """
        num_test = X.shape[0]
        num_train = self.X_train.shape[0]
        dists = np.zeros((num_test, num_train))
        #########################################################################
        # TODO:                                                                 #
        # Compute the l2 distance between all test points and all training      #
        # points without using any explicit loops, and store the result in      #
        # dists.                                                                #
        #                                                                       #
        # You should implement this function using only basic array operations; #
        # in particular you should not use functions from scipy,                #
        # nor use np.linalg.norm().                                             #
        #                                                                       #
        # HINT: Try to formulate the l2 distance using matrix multiplication    #
        #       and two broadcast sums.                                         #
        #########################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        dists=-2*np.dot(X,self.X_train.T)
        a=(self.X_train**2).sum(axis=1)
        b=(X**2).sum(axis=1,keepdims = True)
        dists=np.add(dists,a)
        dists=np.add(dists,b)
        dists=np.sqrt(dists)

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        return dists

    def predict_labels(self, dists, k=1):
        """
        Given a matrix of distances between test points and training points,
        predict a label for each test point.

        Inputs:
        - dists: A numpy array of shape (num_test, num_train) where dists[i, j]
          gives the distance betwen the ith test point and the jth training point.

        Returns:
        - y: A numpy array of shape (num_test,) containing predicted labels for the
          test data, where y[i] is the predicted label for the test point X[i].
        """
        num_test = dists.shape[0]
        y_pred = np.zeros(num_test)
        for i in range(num_test):
            # A list of length k storing the labels of the k nearest neighbors to
            # the ith test point.
            closest_y = []
            #########################################################################
            # TODO:                                                                 #
            # Use the distance matrix to find the k nearest neighbors of the ith    #
            # testing point, and use self.y_train to find the labels of these       #
            # neighbors. Store these labels in closest_y.                           #
            # Hint: Look up the function numpy.argsort.                             #
            #########################################################################
            # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

            
            sort_index=np.argsort(dists[i])
            k_min_index=sort_index[:k];
            closest_y=self.y_train[k_min_index]

            # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
            #########################################################################
            # TODO:                                                                 #
            # Now that you have found the labels of the k nearest neighbors, you    #
            # need to find the most common label in the list closest_y of labels.   #
            # Store this label in y_pred[i]. Break ties by choosing the smaller     #
            # label.                                                                #
            #########################################################################
            # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

            count=np.bincount(closest_y)
            y_pred[i]=np.argmax(count)

            # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

        return y_pred