可分离的隐式Transformer用于可解释单目高度估计
目录
- 摘要
- 1.Introduction
- 2.Related Wrok
-
- 2.1.Monocular Height Estimation
- 2.2.Methods for Understanding Monocular Depth Estimation
- 2.3.Interpretable and Explainable Deep Neural Networks
- 3.方法
-
- 3.1.Unit-level Interpretation of MHE Models
- 3.2.Instance-level Interpretation of MHE Models
- 3.3.Pixel-level Attribution Analysis of MHE Models
- 4.可分离的隐式Transformer
- 5.Experiments
摘要
利用遥感图像进行单目高度估计(MHE)可以高效地生成三维城市模型,以快速响应自然灾害。大多数现有工作追求更高的性能。然而,很少有探索MHE网络的可解释性。在本文中,我们的目标是探索如何从单目图像深度神经网络预测高度。为了全面理解MHE网络,我们建议从多个层面对其进行解释:1)神经元:单位水平(unit-level)解剖。探索学习到的内部深层表征的语义和高度选择性;2) 实例:对象级(object-level)解释。研究不同语义类别、尺度和空间语境对高度估计的影响;3) 属性:像素级(pixel-level)分析。了解哪些输入像素对高度估计很重要。在多层次解释的基础上,提出了一种可解释的可分离的隐式Transformer,为单目高度估计提供一种更紧凑、可靠和可解释的模型。此外,本文还首次提出了一种基于高度估计的无监督语义分割任务。此外,我们还构建了一个新的数据集,用于联合语义分割和高度估计。我们的工作为理解和设计MHE模型提供了新的见解。
1.Introduction
城市灾害监测与城市居民的生活密切相关。三维城市的几何信息可用于城市规划、灾害监测、灾害预测等。在这方面,有效地从遥感图像中获取几何信息对于快速应对时间紧迫的世界事件至关重要,例如自然灾害和损害评估。从图像中估计几何结构是遥感和地球观测的长期目标。激光雷达、雷达、立体摄影测量需要昂贵的设备和复杂的数据处理,而从单一图像预测高度是一种低成本、及时更新的方法。
受单目深度估计(MDE)任务发展的推动,人们提出了多种单目高度估计方法。Mou等人设计了一个用于高度估计的残差卷积网络,并在实例分割任务中证明了其有效性。Christie等人提出从单目倾斜图像估计地心姿态。 由于从单目图像估计高度是一项紧迫的任务,因此提高深部模型的可解释性和可靠性是风险敏感模型应用的首要任务。
对于可解释的模型,之前工作对图像分类和目标检测进行了研究。然而,MHE是一项涉及像素回归的密集预测任务。这使得图像级和对象级的解释方法不适用。与MHE最相关的任务是MDE。Dijk等人研究了用于深度估计的输入单目图像中的重要视觉线索。Hu等人试图找到最相关的稀疏像素来估计深度。You等人首先发现了一些隐藏单元的深度选择性,这为解释MDE模型提供了有希望的见解。然而,仅仅关注单元级或全局解释,忽略了输入图像的语义内容,这不足以解释复杂且分布不均的场景。
虽然MHE与MDE有一些相似的特点,但仍有几个方面使它们截然不同。首先,高度是物体的固有属性,在不同的视角下不应改变。而物体的深度在很大程度上取决于相机的姿势。其次,由于严重的遮挡和纹理缺乏,从俯视图估计高度可能比从街景估计深度要模糊得多。第三,远距离感知图像中的物体类型、比例和场景布局差异很大。这些差异也使得MDE的解释方法不适合直接应用于MHE。
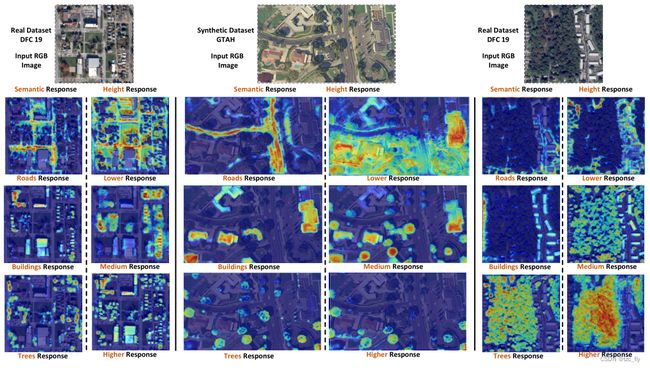
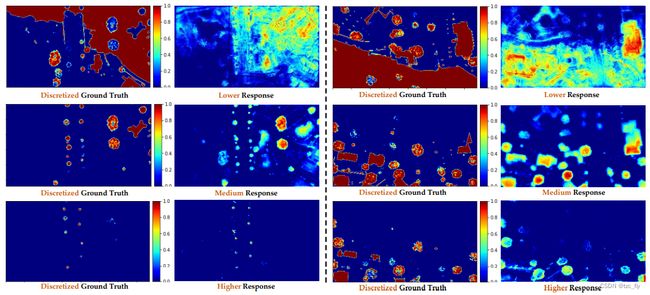
- 图1:MHE网络学习隐式识别不同的语义对象(道路、建筑物和树木)和高度范围。该图显示了GTAH数据集(合成图像)和DFC 2019数据集(real-world)上基于transformer的MHE网络的选择性。
- 图2:高度范围和MHE网络特征图之间高度相关性的可视化。
考虑到上述问题,在这项工作中,我们的目标是:1)从多个层面了解MHE的深层网络;2) 为MHE任务设计可靠且可解释的深度模型。具体而言,我们建议从以下三个层面解释深层MHE模型:
- Neurons:unit-level,探索隐藏单元的属性,以了解MHE模型学到的内部表示。这是固有的可解释机器学习模型的基本组成部分。从这个角度来看,我们发现MHE网络学习不同语义概念和高度范围的分离表示。如图1和图2所示,道路、树木和建筑物会自动识别,并且它们也会根据不同的高度范围进行选择。
- Instances:object-level,基于对MHE网络中神经元的理解,我们研究了语义对象的变化对MHE网络的影响。通过观察MHE网络在这些因素变化下的行为,我们发现语义类、尺度和语境是影响高度预测结果的主要因素。
- Attribution:pixel-level,为了全面了解MHE模型,有必要知道哪些输入像素负责高度估计。基于对MHE网络中神经元的理解,我们提出将高度预测局部地归因于其输入图像。此外,Transformer和CNN都使用局部属性分析进行了分析和比较。
考虑到包含高分辨率高度图和像素语义标签的数据集有限,我们构建了一个新的数据集,名为华盛顿特区(WDC)数据集,以促进提高MHE模型的可解释性和性能的研究。据我们所知,这项工作是首次尝试分析深度网络在单目高度估计任务中的作用。我们的贡献可以总结如下:
- 通过MHE模型学习的深层神经元对高度范围和语义类别都具有高度选择性。基于MHE网络的高类别选择性,我们提出了一种简单而有效的OOD(out of ditribution)MHE方法。
- 基于观察到的类别选择性,我们进行了对象级实验,发现语义类、对象尺度、空间上下文是影响高度预测的主要因素。
- 通过局部attribution分析,我们比较了Transformer和基于CNN的MHE任务模型。结果表明,基于Transformer的网络比CNN具有更强的高度和类别选择性,可以学习更多有效的上下文。
- 在多层次解释的基础上,我们提出了可分离的隐式Transformer,用于学习可解释可分离的表示,以获得更可解释、更高效的MHE模型。
- 基于对高度估计网络的理解,本文首次提出了一种新的无监督语义分割任务。此外,还构建了一个包含RGB和nDSM(归一化数字表面模型)的新数据集,用于联合学习语义分割和高度估计。
2.Related Wrok
2.1.Monocular Height Estimation
随着深度学习的发展,针对MHE的各种方法被提出。Srivastava等人提出在多任务深度学习框架中联合预测高度和语义的标签。Mou等人设计了用于高度估计的残差CNN,并在实例分割任务中证明了其有效性。此外,提出了条件生成对抗网络(cGAN)将高度估计作为图像翻译任务。Kunwar等人利用语义标签作为优先项,提高了大规模城市语义3D(US3D)数据集的高度估计性能。Xiong等人设计并构建了一个大规模基准数据集,用于高度估计任务的跨数据集迁移学习,其中包括一个大规模合成数据集和多个真实数据集。Swin Transformer被用于研究MHE任务的可迁移表征学习。单目高度估计可以广泛应用于高风险的地球观测任务中,但目前还没有研究针对MHE任务的深度学习模型的可解释性。
2.2.Methods for Understanding Monocular Depth Estimation
近年来,单目深度估计得到了广泛的研究。随着深度学习的兴起,人们设计了大量方法来获得更好的性能,包括几何约束学习、多尺度学习、多任务学习方法。为了了解这些MDE网络学到了什么,Dijk等人研究了深度网络在预测深度时使用的重要视觉线索。他们主要关注MDE网络的对象级解释。Hu等人试图只找到一组选定的稀疏图像像素来估计深度。设计了一个单独的网络来预测这些稀疏像素。然而,这些方法忽略了模型已经学习到的固有表示。You等人首先发现了一些隐藏单元的深度选择性,这为解释MDE模型提供了有希望的见解。然而,仅仅关注模型解释中的隐藏单元忽略了输入图像的语义内容。
2.3.Interpretable and Explainable Deep Neural Networks
Interpretable deep models
对于图像分类和目标检测任务,有几种方法试图设计固有的可解释模型。Chen等人提出寻找原型部件,并解释做出最终决定的原因。对于人员再识别任务的可解释性,Liao等人设计了一个模型,显式构建特征地图的匹配过程。Zhang等人通过让每个filter代表特定的对象部分,设计了可解释的CNN。Liang等人通过学习特定于类的filter来训练可解释的CNN,也就是说,鼓励每个filter只考虑少数类。类似地,You等人提出通过为MDE模型设计特定的loss来提高深度选择性。
Explainable deep networks
许多研究人员专注于基于显著性(saliency-based)和基于归因(attribution-based)的方法来解释深层网络。他们旨在强调输入图像的哪些像素对预测结果很重要。然而,基于属性和显著性的方法并不直接适用于密集预测任务,包括MDE和MHE,因为不合理的做法是突出显示所有像素来全局地对密集预测进行属性化。Gu等人提出了一种解释超分辨率网络的局部归因方法。他们选择解释特征,而不是超分辨率任务的像素,这启发了我们对MHE网络像素属性的研究。
3.方法
这项工作的动机有两个方面:1)从多个层面解释MHE网络的行为,以便更好地理解MHE模型;2)为MHE任务设计可靠且可解释的深度模型。图3显示了用于说明多级可解释性框架的整个流程。为了理解学习到的隐藏单元的行为,我们通过可视化特殊深度filter的表示来检查MHE网络的学习知识。基于语义类与高度预测高度相关的发现,我们研究了不同语义对象和属性对MHE网络的影响。最后,基于单元级和对象级解释结果,我们设计了一种像素级局部归因方法来解释MHE网络。在本节中,我们将详细介绍多级解释框架以及可分离的隐式Transformer。
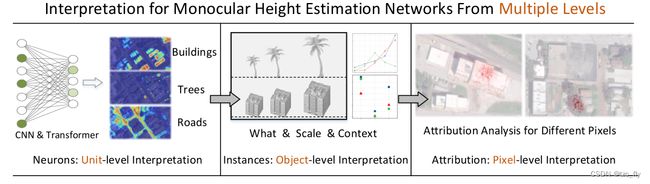
- 图3:考虑了三个层次:1)神经元:单元级网络解剖;2) 实例:对象级解释;3) 属性分析:像素级解释。
3.1.Unit-level Interpretation of MHE Models
不同语义类型的对象通常具有不同的高度属性。因此,高度图中的几何信息应与语义信息相关。受此启发,我们选择研究学习到的内部激活,以找到人类可以理解的表示。从大量深层激活的可视化中,我们发现模型的某些单元对不同的语义类别和高度范围具有选择性。如图1所示,包括道路、建筑物和树在内的不同语义对象仅在高度限制下可利用隐式方式精确定位。这一发现支持了语义信息和几何信息相关的假设。
此外,我们还发现一些神经元对不同的高度范围具有选择性。如图2所示,左栏显示了不同离散化高度范围的mask,右栏是MHE网络的特征图。显然,我们可以看到它们之间有很高的相关性。为了量化网络单元的选择性,我们计算了每个内部单元的类别选择性和高度选择性。在这项工作中,我们采用了Swin Transformer作为高度估计任务的backbone。将 ( x i , y i , h ) (x_{i},y_{i},h) (xi,yi,h)作为数据集 D D D的样本, x i ∈ R 3 , H , W x_{i}\in R^{3,H,W} xi∈R3,H,W是输入图像, y i ∈ R H , W , h i ∈ R H , W y_{i}\in R^{H,W},h_{i}\in R^{H,W} yi∈RH,W,hi∈RH,W是语义分割GT和高度GT。 D D D一共 N N N个样本。我们上采样倒数第二层输出的 k t h k_{th} kth特征图到输入图像大小 F k ( x i ) ∈ R H , W F_{k}(x_{i})\in R^{H,W} Fk(xi)∈RH,W。类别选择和高度选择可以计算为:
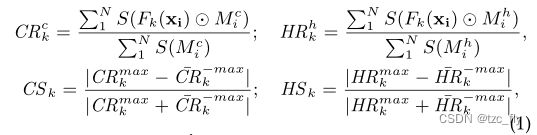
其中, C R k c , H R k c CR_{k}^{c},HR_{k}^{c} CRkc,HRkc是不同类别和高度范围的unit平均响应。 h h h是离散化高度范围的索引, c c c是语义类的索引。 M c M^{c} Mc是一个二进制掩码,表示具有语义类 c c c的像素。 M h M^{h} Mh也是一个二进制掩码,表示高度范围 h h h中的像素。 S ( ⋅ ) S(\cdot) S(⋅)表示矩阵中所有元素的求和运算。我们使用 ⊙ \odot ⊙表示element-wise乘法。根据定义的平均响应 C R k c , H R k c CR_{k}^{c},HR_{k}^{c} CRkc,HRkc,可以计算第 k k k个unit的 C S k , H S k CS_{k},HS_{k} CSk,HSk(值在0到1之间)的类选择性和高度选择性。
选择值较大的unit倾向于更好地响应特定的语义类或高度范围。我们在图2中可视化了具有更高的高度选择性值的特征图,图2显示了特征图与不同高度范围之间的相关性。此外,图4还提出了定量的高度选择性。对于真实数据集和合成数据集GTAH,在不同高度范围内都存在明显的选择性。
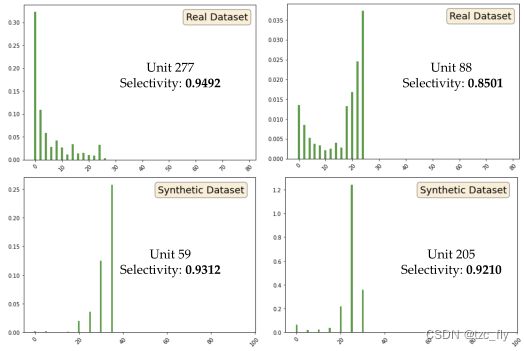
- 图4:在DFC 2019数据集和GTAH数据集上显示高度选择性较大的平均响应。
图5显示了基于transformer的MHE模型的类别选择性。unit 255、87和20的类别选择性大于0.8,它们分别对地面、高植被和建筑类别具有高度选择性。然而,水和高架道路没有明确的选择unit,因为这些类别与地面相比,在高度变化方面没有明确的判别差异。
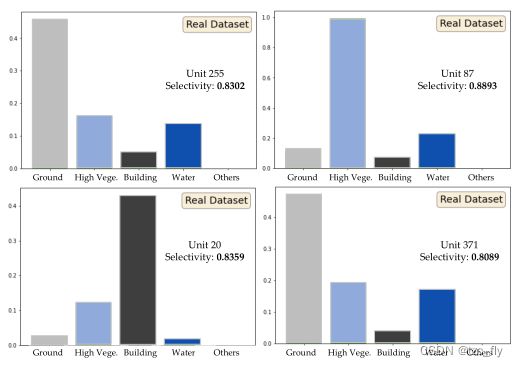
- 图5:类别选择性的unit的平均响应的可视化。
基于MHE网络的高类别选择性,我们提出了一种简单而有效的 ood MHE方法。为了更好地解释这种方法,我们通过向输入图像中添加一些不相关的对象(如奶牛和瓶子)来构造一个ood样本。如图6所示,我们添加了一个树(in-distribution)对象作为比较样本。与原始输入相比,我们可以看到,在几乎所有的特征图中,分布外的对象(奶牛和瓶子)都高亮显示。这意味着网络无法识别这些分布外的对象。相比之下,添加的树对象由MHE模型识别,并且仅在树选择特征映射中高亮显示。

- 图6:在几乎所有的特征图中,分布外的对象(奶牛和瓶子)都会高亮显示,这意味着这些分布外的对象不会被网络识别。相比之下,添加的树仅在树选择特征映射中高亮显示。
为了量化这一点,我们建议计算特征图中像素的方差。给定特征图 F ( x i ) ∈ R K , H , W F(x_{i})\in R^{K,H,W} F(xi)∈RK,H,W,我们沿通道normalize: F ′ ( x i ) = F ( x i ) ∑ 1 K F k ( x i ) F'(x_{i})=\frac{F(x_{i})}{\sum_{1}^{K}F^{k}(x_{i})} F′(xi)=∑1KFk(xi)F(xi),然后,我们可以计算沿通道维度的每个像素的 F ′ ( x i ) F'(x_{i}) F′(xi)方差。最后我们可以定义异常响应图 R o o d = I − v a r ( F ′ ( x i ) ) R_{ood}=I-var(F'(x_{i})) Rood=I−var(F′(xi))作为ood的衡量。一些可视化示例如图7所示。可以看出,检测到的ood对象具有较高的响应值。
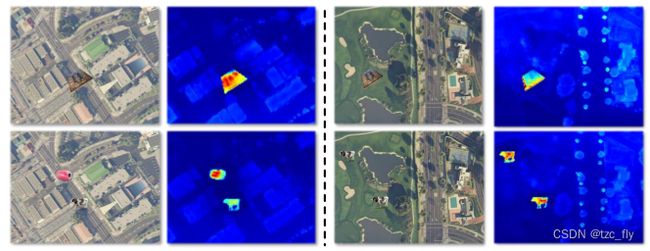
- 图7:ood结果的可视化。ood的对象在异常响应图 R o o d R_{ood} Rood中突出显示。
3.2.Instance-level Interpretation of MHE Models
考虑到学习unit对不同的语义对象具有高度选择性,通过改变原始输入图像的语义来研究MHE网络的行为是很自然的。因此,为了保留原始输入的语义概念,我们选择修改原始输入图像的对象实例。
具体来说,受人类认知过程的启发,我们探讨了改变对象实例的语义类、规模和阴影状态的影响。首先,我们为语义类别 c ∈ { r o a d , t r e e , b u i l d i n g } c\in\left\{road,tree,building\right\} c∈{road,tree,building}和尺度 s ∈ { s 1 , s 2 , . . . , s 5 } s\in\left\{s_{1},s_{2},...,s_{5}\right\} s∈{s1,s2,...,s5}定义模板 t s c t_{s}^{c} tsc。假设每个类别模板的原始比例(面积) 为 s t s_{t} st,然后 { s 1 = 0.3 ∗ s t , s 2 = 1.0 ∗ s t , s 3 = 1.5 ∗ s t , s 4 = 2.5 ∗ s t , s 5 = 3.0 ∗ s t } \left\{s_{1}=0.3*s_{t},s_{2}=1.0*s_{t},s_{3}=1.5*s_{t},s_{4}=2.5*s_{t},s_{5}=3.0*s_{t}\right\} {s1=0.3∗st,s2=1.0∗st,s3=1.5∗st,s4=2.5∗st,s5=3.0∗st}。
为了研究语义类别的变化对高度预测的影响,我们对测试数据集中的每幅图像 x i x_{i} xi选择一个合适的patch,用预定义的模板 t s c t_{s}^{c} tsc替换语义类{road,tree,building}。实验结果如图8所示。我们可以看到,在替换不同语义类别的对象后,预测的高度会像预期的那样发生变化。这表明高度预测结果与物体的语义类别高度相关。
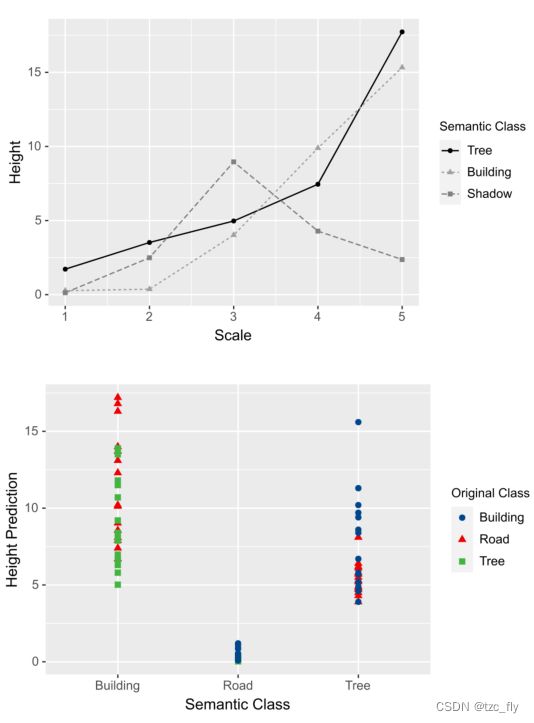
- 图8:对象级别的变化对MHE网络影响的可视化。
为了探索对象尺寸变化的影响,对于测试集 D D D中的每个图像,我们首先在原始图像中选择合适的位置{ p x , p y p_{x},p_{y} px,py}。然后,对于每一个尺寸 s ∈ { s 1 , s 2 , . . . , s 5 } s\in\left\{s_{1},s_{2},...,s_{5}\right\} s∈{s1,s2,...,s5},我们将预定义的模板 t s c t_{s}^{c} tsc放置在所选位置。由于改变道路的比例没有意义,我们只对建筑物和树木对象进行实验。图8显示了每个尺度的平均高度结果。可以看出,一般来说,对象比例越大,预测的高度值越大。然而,值得一提的是,如果尺度太小,网络可能无法识别对象。此外,我们还探讨了对象阴影的不同比例的效果。在我们的实验中,高度预测与阴影的比例没有明显的相关性。
3.3.Pixel-level Attribution Analysis of MHE Models
由于MHE是一项密集的预测任务,因此在全局范围内解释所有像素的MHE网络无法提供有意义的解释信息。通过unit级和object级的分析,我们发现如果在特征图中无法识别对象的语义类,那么预测结果将是不可靠的。这表明特征图上物体的存在是高度预测的一个基本和重要因素。因此,我们设计了一种基于特征存在和路径积分梯度的局部属性分析方法,以在像素级解释MHE网络。
对于输入图像 x x x, F h ( x ) F_{h}(x) Fh(x)表示网络预测的高度图。我们定义 D p x , p y ( x ) D_{px,py}(x) Dpx,py(x)将一个局部对象的存在量化为 D p x , p y ( x ) = ∑ i ∈ [ p x , p x + n ] , y ∈ [ p y , p y + n ] F h ( x ) i j D_{px,py}(x)=\sum_{i\in[px,px+n],y\in[py,py+n]}F_{h}(x)_{ij} Dpx,py(x)=i∈[px,px+n],y∈[py,py+n]∑Fh(x)ij其中, n n n是被选择patch的window size。为了挖掘导致一个物体存在的重要像素,我们使用整个黑色图像作为基线输入 x ′ x' x′。为了获得所选局部patch的属性图,我们需要沿着从 x ′ x' x′到 x x x逐渐变化的路径累积梯度。注意,对于基线图像 x ′ x' x′,MHE网络 F h ( x ′ ) F_{h}(x') Fh(x′)的输出不是零。
然后,可以通过以下公式计算局部patch I G IG IG 的积分梯度的第 i i i维:
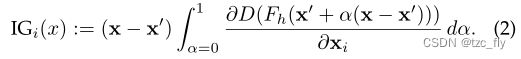
在这项工作中,我们使用线性路径函数来定义 α \alpha α。具体来说,我们用 m m m步从0到1平滑地插值 α α α。实际上,我们通过沿 m m m步进行以下求和来近似计算公式2中定义的积分:
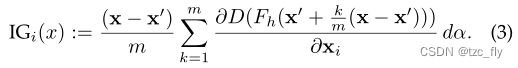
根据经验,在我们对真实数据集和合成数据集的实验中,将 m m m设置为100对MHE网络都很有效。
4.可分离的隐式Transformer
基于语义选择性的发现,我们为从多个层面理解MHE模型奠定了一个新的视角:1)语义选择性激发了instance-level解释,并提供了实例替换有意义的原因;2) 实例级实验进一步表明,通过局部属性分析来检测局部语义对象的存在性是一种有效的像素级解释方法。
为了更好地利用语义选择性,在这项工作中,我们进一步提出了一种可分离的隐式Transformer(DLT)网络来显式地建模不同语义类的表示。通过将MHE模型的深层神经元划分为不同的语义组,提出了一种新的无监督语义分割方法。具体来说,DLT利用transformer主干更好地了解不同像素之间的成对关系。接下来,为每个语义类预测一个潜在的随机变量,该变量可用于生成特定类的语义分割图。
我们观察到,最后一层的不同神经元对不同的语义类有特定的反应,并且有多个神经元负责特定的类。因此,为了实现可解释示学习,我们首先将这些神经元聚集到不同的语义组中。形式上,给定一个预训练的基于transformer的深度网络,在最后一层有 n n n个神经元,将权重用K-means聚类为 K K K组。注意,对于每个预先训练的深度模型,我们只需要对神经元进行一次聚类,而不需要在每次推理时对特征映射进行聚类。基于预测的聚类index,我们可以进一步得到 K K K组特征图。每个语义组包含 n i n_{i} ni个特征图。
5.Experiments
- 图9:华盛顿特区数据集样本的可视化。以农村、森林、水和城市的patch为例。对于每个patch,将显示正射影像、nDSM(高度图)和语义图。
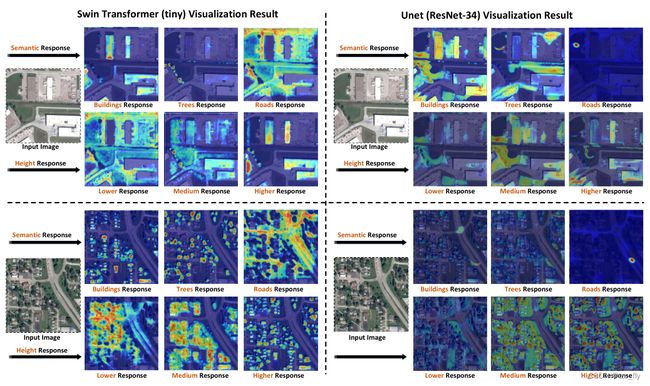
- 图10:基于transformer的模型可以学习不同语义对象的可解释表示。而基于UNet的模型的特征映射在某种程度上是纠缠的。
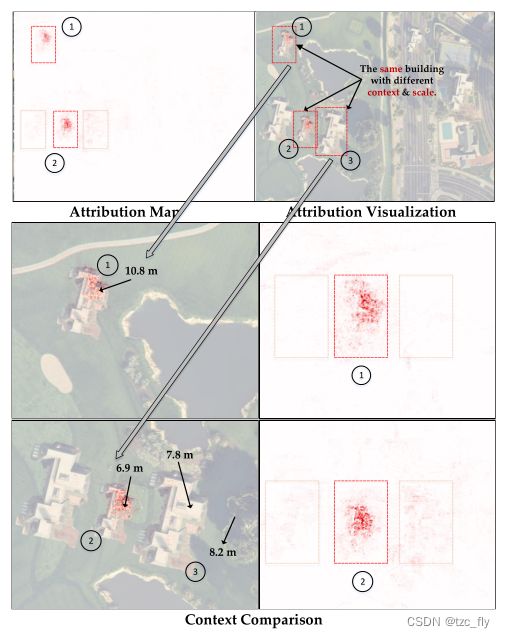
- 图11:比较同一对象模板但不同空间上下文的属性图。
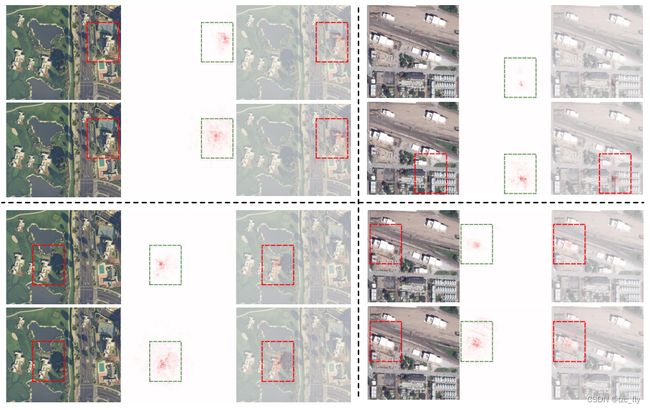
- 图12:基于Transformer和基于UNet的MHE网络属性图的比较。我们可以看到,基于Transformer的模型可以学习利用更有效和紧凑的上下文。
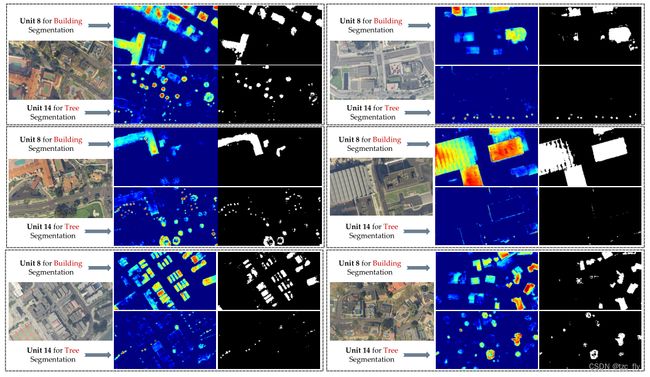
- 图13:GTAH数据集上提出的“SwinT(16个单元)+DLT”的无监督语义分割结果。图中显示了第八unit(建筑)和第十四unit(树)的特征图和分割图。
- 图14:DFC 2019数据集上提出的“SwinT(16个单元)+DLT”的无监督语义分割结果。图中显示了第三unit(建筑,左侧)和第七unit(树,右侧)的分割图。与对应的方法相比,我们的DLT可以获得明显更好的分割结果。