matlab - 信号平滑、移动平均滤波

matlab - 信号平滑、移动平均滤波

对信号进行平滑操作的重要性不言而喻

1.信号提取

matlab内置了一个这样的数据：某个地方一个月内的温度变化数据，1小时测量一次，所以总数据量是24*31。

可以以这个数据为例子，探究一些数据平滑的方法。该数据如下：

clear all
close all
load bostemp
days = (1:31*24)/24;
plot(days, tempC)
axis tight
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')

上图就是一个月温度的真实变化，凹凸不平。

如果你想看到这一个月内温度的总体变化趋势，而不是关注每天、没小时的变化情况，这时小变化对我们的目的来说就成了噪声，那么就可以将这个数据进行平滑处理，更能反映一个稍大的趋势。移动平均滤波就是一种非常简单有效地平滑方法。

2.均匀移动平均滤波

就不写通用式了，还是举个例子方便理解，有一个数据集x(n)，如果取平均窗长为N=3，那应该有：
$$y(0)=(1/3)\ast [x(0)]$$

$$y(1)=(1/3)\ast [x(0)+x(1)]$$

$$y(2)=(1/3)\ast [x(0)+x(1)+x(2)]$$

$$y(3)=(1/3)\ast [x(1)+x(2)+x(3)]$$

$$......$$

下面取N = 24对这个温度数据tempC进行平滑

hoursPerDay = 24;
coeff24hMA = ones(1, hoursPerDay)/hoursPerDay;

avg24hTempC = filter(coeff24hMA, 1, tempC);
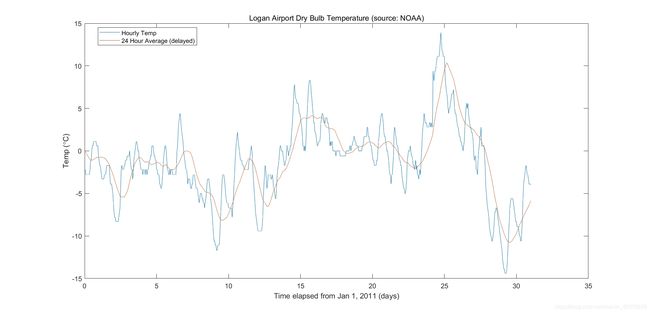
plot(days,[tempC avg24hTempC])
legend('Hourly Temp','24 Hour Average (delayed)','location','best')
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')

输出数据显然平滑了，更能反映一个大的温度变化趋势。当然，平滑后的数据丢失了许多细节。

可以用数字信号处理的观点分析这个平滑过程，移动平均滤波其实就是一个简单的FIR低通滤波器，系统函数h(n)的长度为N，并且对于所有的n都有h(n) = 1/N。这样的系统函数在时域上是个矩形，那么在频域就时sa函数，显然是一个低通滤波器，把高频的量去掉，保留了低频，也就是更大尺度的变化趋势。

细心可以发现，总的来说输出比输入延迟了 (N-1)/2 个单位，这可以用信号与系统的时移性质解释，实际上就是该FIR滤波器的群延时，是个常数。本节重点不在频谱分析，分析就此带过。

移动平均滤波简单还是简单，但是计算量非常大，例如，这里L = 31*24=744个数据，以N =24为平滑窗长，则约需要进行 LN = 1.78万次乘法，L(N-1) = 1.7万次加法。可以使用快速卷积去实现，这样效率更快。

3.均匀移动平均滤波 - 补偿延时

上面分析到一般移动平均滤波延时了（N-1)/2 ，可以进行补偿

fDelay = (length(coeff24hMA)-1)/2;
plot(days,tempC, ...
     days-fDelay/24,avg24hTempC)
axis tight
legend('Hourly Temp','24 Hour Average','location','best')
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')

这样就得到了我们想要的一个月总体的温度变化情况

4.提取包络线

如果想得到这个月温度的最高温和最低温的变化情况，可以使用提取包络线的办法。

[envHigh, envLow] = envelope(tempC,16,'peak');
envMean = (envHigh+envLow)/2;

plot(days,tempC, ...
     days,envHigh, ...
     days,envMean, ...
     days,envLow)
   
axis tight
legend('Hourly Temp','High','Mean','Low','location','best')
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')

5.加权移动平均滤波器

一般的移动平均滤波器的权值时一样的，也可以调整权值。例如，可以使用二项分布的系数作为权值，这时可以用更少的窗长获得更好地平滑效果。这也可以用数字信号处理进行分析，二项分布的系数在时域上比矩形更加接近sa函数，所以对高频分量的滤除效果更好。

h = [1/2 1/2];
binomialCoeff = conv(h,h);
for n = 1:4
    binomialCoeff = conv(binomialCoeff,h);
end

figure
fDelay = (length(binomialCoeff)-1)/2;
binomialMA = filter(binomialCoeff, 1, tempC);
plot(days,tempC, ...
     days-fDelay/24,binomialMA)
axis([2.5,6.5,-3,1])
legend('Hourly Temp','Binomial Weighted Average','location','best')
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')

6.指数移动平均滤波

指数型移动平均滤波的基本模型是：
$$y(k)=a\ast x(k)+(1-a)\ast y(k-1)$$
其实就是一个简单的IIR滤波器。显然，但a越小，当前输入对输出的影响越小，也就越平滑。可以继续推广到跟高阶。这种滤波器可以用更小的阶数实现比一般移动平均滤波更好地平滑效果。

alpha = 0.20;
exponentialMA = filter(alpha, [1 alpha-1], tempC);
plot(days,tempC, ...
     days-fDelay/24,binomialMA, ...
     days-1/24,exponentialMA)

axis([17,20,-1,3])
legend('Hourly Temp', ...
       'Binomial Weighted Average', ...
       'Exponential Weighted Average','location','best')
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')

7.S-G滤波器

全称叫Savitzky-Golay滤波器，是使用多项式对滑窗内最小二乘法拟合。

cubicMA   = sgolayfilt(tempC, 3, 7);
quarticMA = sgolayfilt(tempC, 4, 7);
quinticMA = sgolayfilt(tempC, 5, 9);
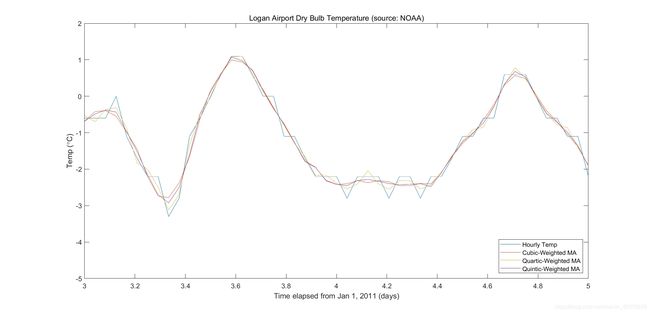
plot(days,[tempC cubicMA quarticMA quinticMA])
legend('Hourly Temp','Cubic-Weighted MA', 'Quartic-Weighted MA', ...
       'Quintic-Weighted MA','location','southeast')
ylabel('Temp (\circC)')
xlabel('Time elapsed from Jan 1, 2011 (days)')
title('Logan Airport Dry Bulb Temperature (source: NOAA)')
axis([3 5 -5 2])

8.中值滤波

上面讲的滤波器不管如何，当信号是突变型的时候，就无能为力了，因为上述的滤波器本质上都是加权多项式的移动平均滤波器，例如下面这个时钟信号例子，我们希望把时钟信号的噪声滤除掉。

load clockex

yMovingAverage = conv(x,ones(5,1)/5,'same');
ySavitzkyGolay = sgolayfilt(x,3,5);
plot(t,x, ...
     t,yMovingAverage, ...
     t,ySavitzkyGolay)

legend('original signal','moving average','Savitzky-Golay')

可以看到，滤波后的数据要么产生了尖峰，要么变化较慢，都不符合我们的目的。

这时可以采用中值滤波，也可以叫中位值的方法。中值滤波的原理是取一串数据，然后对其排序，取中位数作为当前的数据

中值滤波采用的全是原来的数据，只是进行了排序和取舍。除了这个时钟信号的例子，中值滤波还可以方便地滤除信号中一些尖峰突刺，例如超声波传感器就很常用。

yMedFilt = medfilt1(x,5,'truncate');
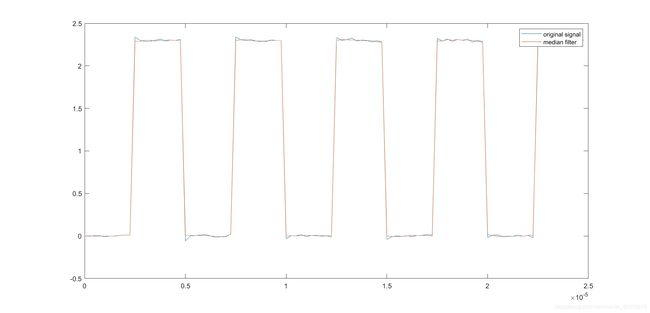
plot(t,x, ...
     t,yMedFilt)
legend('original signal','median filter')

可以看到这时候滤波效果非常好

9.Hampel 滤波器

中值滤波滤波也有一些缺点，例如当数据有尖峰毛刺确是可以将其滤除掉，在某些情况下我们希望只将突兀的值滤除掉，而保留原来的信号，但是中值滤波这也将部分有用的信号滤除掉，例如下面这个例子

load train
y(1:400:end) = 2.1;
plot(y)

我们给原信号加上了一些尖峰点，如果我们采用中值滤波的方法希望将这些尖峰点滤除掉，而保留原信号

hold on
plot(medfilt1(y,3))
hold off
legend('original signal','filtered signal')

利用中值滤波显然可以将外加的尖峰毛刺滤除掉，但是原信号也变了，这不是我们想要看到的

在这种情况下，可以使用Hample滤波器，它与中值滤波器有些相似，但是不是简单地取中位数，也不会随便就把尖峰毛刺扔掉。Hample滤波器会计算附近数据的标准差和均值，以均值为中心，如果该值相差了好几个标准差，才把该值替换成均值与最大能接受的标准差偏差。

hampel(y,13)
legend('location','best')

可以看到，Hample滤波器也会改变原信号的一些点，但是相比一般中值滤波已经好很多了

10.总结

本节介绍了许多数据平滑的办法。均匀移动平均滤波器是最简单的办法，可以有效消除高频变化，让我们看到数据更大的一个趋势。还可以实际情况改变均匀的权值让效果更好，如二项式拟合和S-G滤波器。指数移动平均滤波让输出数据不断递归，用更低的计算量实现比移动平均滤波器更好地效果。如果需要去除尖峰点，可以使用中值滤波和Hample滤波。