(数学建模)评价类-主成分分析
非原创,本人只是初学数学建模,发现网上资料都不全,知识做了一个汇总工作,方便别人查阅,方便自己回忆,侵权立刻删除
从笔记整理出来,可读性可能不强,但是个人认为相对比较全面,可以看附带的链接相对比较清晰(资料)
目录
一、模式是干什么的
1.1基本原理
1.2假设(假设检验用SPSS,后面介绍)
1.3计算步骤
二、算法是干啥的,算法和模型怎么对应
2.1程序清单
1.2部分代码的作用
1.3关键程序解释
三、SPSS
(matlab代码用来进行主成分评价,spss用来判断主成分的前提二是否满足)
一、模式是干什么的
1.1基本原理
1、通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量(主成分)
2、多变量转化为变量个数少但得到的信息较多
3、主成分分析:分析数据是否具有主成分和主成分效果如何
先进行分析,如果效果好,才可以使用主成分分析
主成分分析评价:根据主成分分析的结果直接评价
4、最后得到结果:第N主成分、累计贡献率(最少保证所有主成分累计对原始数据的贡献达到80%)
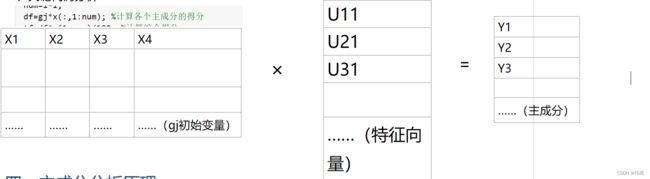
5、10各自变量x同时影响因变量y,但各x之间具有相关性,通过主成分分析得到各个x的权重/成分(对原始数据的贡献度),从而进行变换得出第一主成分、第二主成分、加入前6个成分权重累积到80%以上,那这6个就是主成分,后续做计算就用这个指标。
6、主成分分析方法之所以呢个够降维,本质是因为原始变量之间存在较强的相关性,若原始变量之间的相关性较弱,则主成分分析不能起到很好的降维效果。
7、几何意义
如图所示,平面上散落着N个点,无论是沿x1轴方向,还是沿x2轴方向,均有较大的离散性,即这些点所代表的信息由两个指标x1,x2所决定,若只考虑x1和x2中的任何一个,原始数据中的信息均会有较大的损失。
但是我们将坐标轴进行一个旋转操作,得到新的坐标轴y1和y2,如上图所示,则会发现这些点只在y1方向上由较大的离散性,即y1可以代表原始数据的绝大部分信息。
也就是说原来需要2个指标才能表示的信息,经过一些处理,变成只需要1个指标,而且不会损失太多的信息,即所谓的降维。
8、数学原理
求解主成分,就是根据数据源的协方差阵,求解特征根,特征向量的过程。
一个结论:主成分可以利用协方差阵的特征值对应的单位正交特征向量来表示。
贡献率等于单个特征根除以总特征根之和。
协相关系数矩阵的特征向量为主成分系数
特征值除以总的特征值之和就是相应主成分分析的占比。
9、缺点提取的主成分必须能给出负荷实际北京和意义的解释,否则主成分将空有信息量而无实际含义,维数降低的“利”可能抵不住主成分含义不如原始变量清楚的“弊”
1.2假设(假设检验用SPSS,后面介绍)
假设1:观察变量是连续变量或有序分类变量(取值的各类别之间存在程度上的差别,给人以半定量的感觉),前者是-0.111,0.112这种,后者为治愈、显效、好转、无效这种。
假设2:变量之间存在线性相关关系
1.3计算步骤
资料1
1、对原始数据进行标准化处理
(1)计算相关系数矩阵R
| x |
y |
z |
|
| x |
|||
| y |
|||
| z |
(2)计算相应的特征值、特征向量
2、构建新的主成分的指标变量
3、选择合适的主成分,计算综合评价值。
二、算法是干啥的,算法和模型怎么对应
2.1程序清单
clc,clear
load('pc.txt'); %把原始数据保存在纯文本文件gj.txt中
sum_0=0;%数值初始化
i=1;%数值初始化
gj=zscore(pc); %数据标准化
r=corrcoef(gj); %计算相关系数矩阵
%下面利用相关系数矩阵进行主成分分析,x的列为r的特征向量,即主成分的系数
[x,y,z]=pcacov(r); %y为r的特征值,z为各个主成分的贡献率
while ((sum_0<98)&(z(i)>2))%根据累积贡献率确定主成分个数
n=size(z);
sum_0=sum_0+z(i);
i=i+1;
end
f=repmat(sign(sum(x)),size(x,1),1); %构造与x同维数的元素为±1的矩阵
x=x.*f; %修改特征向量的正负号,每个特征向量乘以所有分量和的符号函数值
num=i-1;
df=gj*x(:,1:num); %计算各个主成分的得分
tf=df*z(1:num)/100; %计算综合得分
[stf,ind]=sort(tf,'descend'); %把得分按照从高到低的次序排列
stf=stf';
ind=ind';
fprintf('各成分的贡献率:\n');disp(z);
fprintf('综合得分:\n');disp(stf);
fprintf('排名:\n');disp(ind);
1.2部分代码的作用
1、zscore标准化eg1,2,3---1,0,1
标准化的目的是为了解决量纲的不同而产生的偏差
2、corrcoef
| x |
y |
z |
|
| x |
|||
| y |
|||
| z |
一图点醒梦中人啊
3、向量是n×1阶,矩阵是m×n阶
4、pcacov(主成分分析函数)
5、[coeff,latent,explained] = pcacov(V)
coeff:特征向量
latent:特征值
explained:每个特征值的占比
我对他的理解是当贡献度小于98,而写每项主成分的贡献度大于2时执行循环?
解答:explained(z)返回的值就是从小到大排列
若存在数λ使AX=λx有非平凡解x,则称λ为A的特征值,x称为对应于λ的特征向量。
A对特征向量的作用是很简单的,只是对特征向量进行了拉伸,而特征值表达了它的方向和大小。
6、size(A),若A是一个3×4矩阵,则返回向量[3 4]
7、
8、sort(,direction)“ascend”、“descend”分别表示升序和降序排列
9、s=s’,转秩
10、fprintf将数据写入文本文件,disp显示变量内容
1.3关键程序解释
计算各个主成分的得分
三、SPSS
资料2
资料3
1、判断假设二:(1)相关性矩阵,用这个来判断各变量之间的线性相关关系,从而让决定变量的取舍,即如果某一个变量与同一分组中其他变量之间的关联性不强,则认为与其他变量测量的内容不同,在主成分提取中不应该纳入该变量
(2)KMO检验(用于主成分提取的数据情况),一般来说,KMO检验系数分布在0到1之间,如果系数值大于0.6,则认为样本负荷数据结构合理的要求。但既往学者普
2遍认为,只有当KMO检验系数值大于0.8时,主成分分析的结果才具有较好的实用性。
根据系数对应关系表,我们认为本研究数据结构很好(meritorious),具有相关关系,满足假设2。
(3)Bartlett's检验
2、总方差解释,来得出成分1、2的占比
3、成分矩阵,来得出每个成分的组成,这里的特征向量不能直接用,得归一化
4、碎石图,表示主成分的占比
5、通过相关性矩阵来判断各变量之间的线性相关关系,从而决定变量的取舍。
即如果某一个变量与同意分组中其他变量之间的关联性不强,我们就认为该变量
与其他变量测量的内容不同,在主成分提取中不应该纳入该变量。
两个,怎么判断有没有主成分,那个特征值数量的设计
6、数据变异程度是观测值与一个中心值散布或分散的量,用来解释点是倾向于聚集在中心周围还是更广泛地分散。
7、公因子方差结果:研究中有多少变量数据结果就会输出多少个成分,本数据有10个变量就会有10个成分。“初始”栏表示当所有成分都纳入时,每个变量被解释程度为1,因为没有剔除任何信息。“提取”栏是当我只保留选中的成分时,变量变异被解释地程度,只保留了部分成分,所有变量变异被解释的程度会降低,
换言之,反映了本次主成分分析从每个原始变量的代表程度,即对每个原始变量的代表程度。(比如V8没有很好的线性相关性,此时他的此项指标很低,然后特征值占比也很低)
8.总方差解释,总计为特征值,方差百分比为特征值除以总的特征值,即贡献率。
9、成分矩阵:反映了提取的多个主成分与原始变量的相关性,可以得出主成分y与原始变量x1、x2…的相关性较强,然后根据原始变量得出主成分代表的物理意义,将多个原始变量总和为几个综合指标。
10、主成分变量的选择一般可以找碎石图拐点处。
四、不懂的问题
1、(程序)这一步的作用是什么