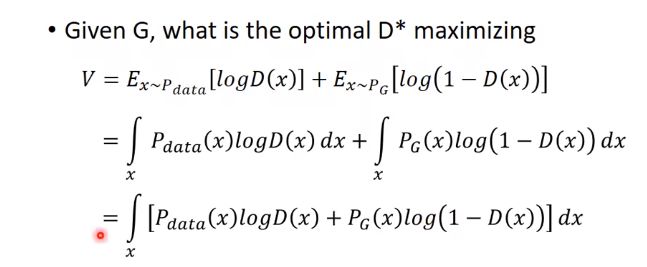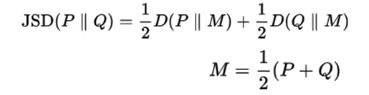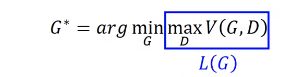通俗易懂生成对抗网络GAN原理（二）

生成对抗网络（Generative Adversarial Network, GAN）的原理

学习李宏毅机器学习课程总结。
前面学习了GAN的直观的介绍，现在学习GAN的基本理论。现在我们来学习GAN背后的理论。

引言

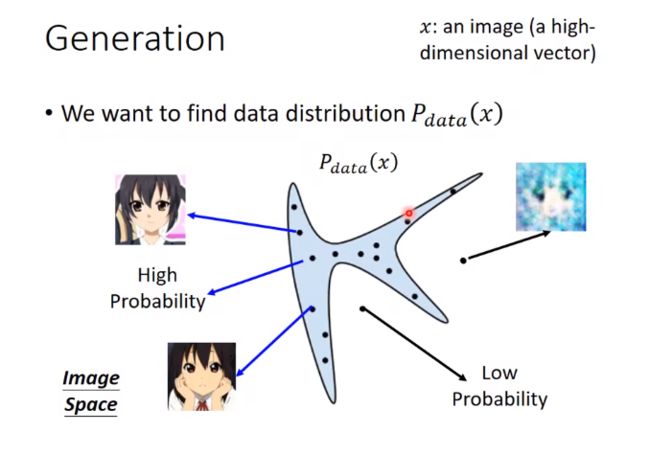
假设x是一张图片（一个高维向量），如64 * 64 * 3的图片，每个图片都是高维空间中的一个点。为了画图方便，我们就画成二维上的点。在高维空间中，只有一小部分采样出来的点符合我们的数据分布（如：整个图中只有蓝色区域采样的点的才是人脸，其他地方的就不是）。
我们想要产生的图片，其数据分布为Pdata。
目的： 让机器找出这个分布。

原始做法

在有GAN之前，人们怎么做生成任务呢？

最大似然估计 （Maximum likelihood estimate）。

• 假设数据集的数据分布为Pdata(x)
  比如数据集为二次元人物，我们也不知道Pdata长什么样
• 假设生成数据分布为PG(x; θ)
  希望找到θ，使得PG(x; θ)和原始未知分布Pdata(x)越接近越好
  如：服从高斯分布，θ就是均值和方差
• 从Pdata(x)里采样一组样本{x1, x2, …, xm}
• 对每个样本，计算其似然：PG(xi; θ)
  
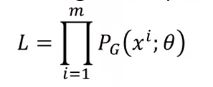
  找到一个θ*，使得该似然值最大

下面有个很重要的概念：
最大似然估计 = 最小KL散度

下面证明：

注：求最大值的θ，多个log不影响，为了乘积变加和

我们可以先回顾一下KL散度的定义：
设P(x)和Q(x) 是随机变量X 上的两个概率分布，则在离散随机变量的情形下，KL散度的定义为：

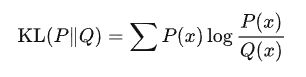
在连续随机变量的情形下，KL散度的定义为：

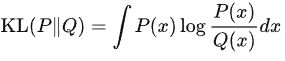
接着上面的，所以：
下面多加了一项（红框），对结果不影响对吧，是为了和KL散度有关。

所以，生成模型目的等价为：最小化分布PG和分布Pdata的散度。

如何定义一个广义的PG？
如果分布为简单的高斯分布，我们可以计算PG(x; θ)，但实际数据都是更复杂的数据，有更复杂的分布，所以无法计算出PG的似然。怎么办？有人提出Generator。

GAN的做法

Generator

图像生成任务在80年代就有人做，那个时候人们就是用高斯模型做，但生成的图片非常非常模糊，不管怎么调整均值和方差，都出不来想要的结果。所以需要更广义的方法做生成任务，即生成对抗网络。

G怎么做生成呢？
从高斯分布中采样的数据z（也可以是其他分布,，如均匀分布等，那到底哪种分布输入好呢？其实都可以，对输出的影响不是很大，因为G都能给它变成更复杂的分布），输入网络G，得到输出x。

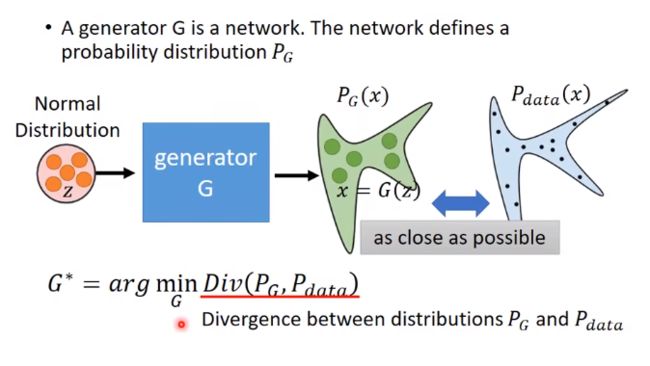
我们希望概率分布PG和Pdata越接近越好，也就是最小化它们的某种散度Divergency（有很多散度，不一定是KL散度）。

那怎么计算这个散度呢？
Pdata和PG的概率分布公式我们不知道，所以不知道怎么算。所以人们想到了判别器Discriminator。

Discriminator

虽然我们不知道Pdata和PG的概率分布公式，但我们可以从这两堆数据里分别采样一些出来。

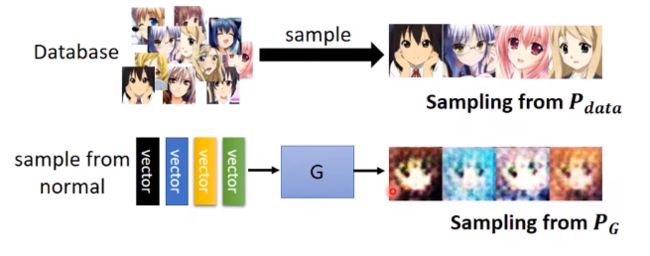
GAN的神奇之处就在于，可以通过D来量这两堆数据之间的散度。

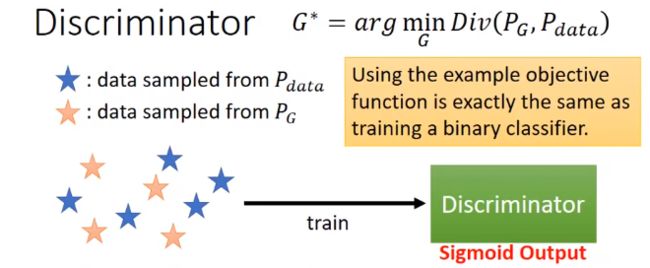
把从Pdata和PG分布里取出的样本数据输入D，训练：

D相当于二分类器，希望对真数据Pdata，输出分数越大越好；对生成数据PG，输出分数越小越好。训练的D的结果，就会告诉我们PG和Pdata他们之间的散度有多大。

训D的时候，G的参数是固定住的。

如果你机器学习基础很好的话，就可以看出这个D的优化函数和二分类器的式子一模一样。

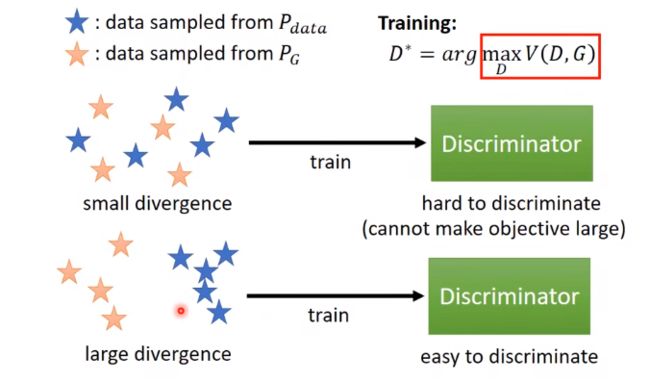
神奇的地方是，当你训完D，你可以得到一个最小的loss或最大的V(D, G )，而这个值和某个JS散度有一些关系，甚至可以说它就是JS散度。

如果D很难区别两类数据的不同，loss就下不去，目标函数就不会得到最大，意味着这两堆数据很相似很接近，他们之间的散度就是很小的。反之亦然。

GAN的数学原理

证明

为什么训练目标函数和散度有关呢？

下面证明：

假设：D(x)可以是任何函数

上式相当于，找到一个D，让积分里面的部分最大：

为了看起来方便，让Pdata = a, PG = b, D(x) = D。

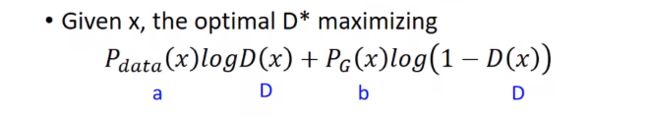
可得到如下，求导，让导数为0。就可得到D*

此时得到局部最大。
接下来，把刚才求得的D*代入目标函数：

得到下式：

为了把它整理成像JS散度，就作一些变换，分子分母同除以2：

把分子的1/2都提出来，放到前面，就是2log(1/2)，或 -2log2。

最后式子可以写成如下：

回顾一下JS散度的公式：

所以可以看到，目标函数和JS散度的关系。

那如果把目标函数写的和上面的不一样，那就是在量不同的散度。

现在看生成器G的目标函数，那就是尽量生成最真的数据，让PG和Pdata越接近，即让它们之间散度最小。

但， Div(PG, Pdata)没有办法算，但上面证明了最小化散度就等于最大化V(D, G)。所以可以把Div(PG, Pdata)替换掉，变成如下：

问题变成min&max问题，看着比较复杂，那么下面举个简单的例子来说明。

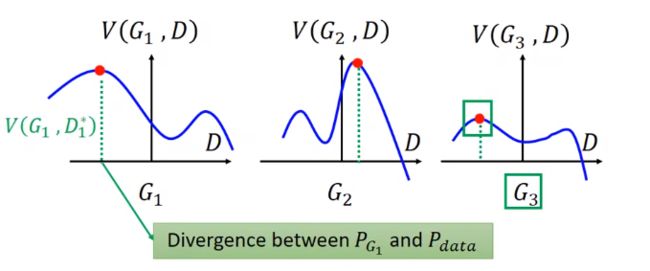
• 假设：我们只有三个生成器G。现在要求解下式：
  
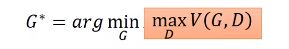
  也就是这三个G是已知的，定的。横坐标代表D，假设D可以用一个参数来操作，横坐标在改变的时候，代表你选择了不同的D，如蓝色曲线所示，实际的D由几百万个的神经网络参数控制的，非常复杂，这里为了解释原理只是简化成一条曲线。
  那minG 和maxD 在图中表示什么呢？
  固定G时，曲线最大值红色点表示max V(G,D)，接下来寻找minG，这几个G哪个最好呢？也就是找哪个最min，显然三号生成器G3。
  绿线的高度就代表PG和Pdata的距离，即它们之间的散度。

算法

如何求解：

之前，我们学到训练GAN的步骤，固定G，训D，固定D，训G，然后重复该过程，这个过程其实就是在解该式。

那为什么这个过程就是在解这个式子呢？

把蓝框的这部分先用L(G)表示，就是假设最大的这个值是L(G)。

那问题就变成，你要找个最好的G，使得L(G)值最小。这个问题就和一般网络一样，用梯度下降法求解。

但是，现在有个麻烦的事，就是L(G)式子里有max，那L(G)还可不可以作微分呢？
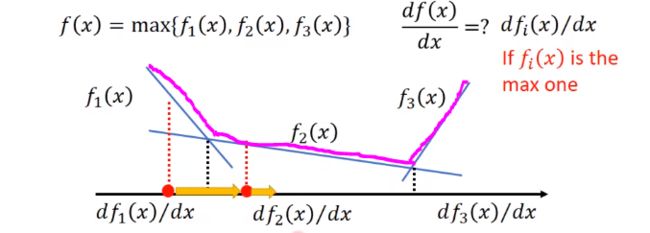
可以的，比如有个式子f(x)长这样：

不同的x值，对应的f(x)不同，看看现在的x能让哪个f(x)最大，就对哪个f(x)微分。

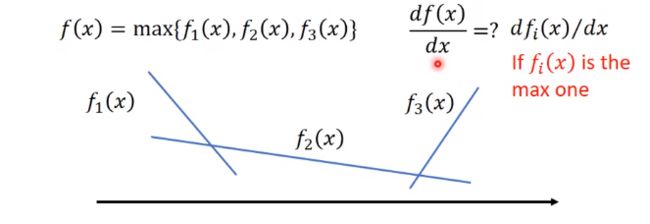
f(x)的最大值就是我画出的桃红色线。
再通俗一点说，就是拿到一个x，求出f1(x),f2(x), f3(x)，看谁的值最大，就把谁拿出来做微分。
比如有个x，先算出来f1(x)最大，然后梯度下降，比如向右移动一点，可能移动到了另外一个区域f2,那就此时f2(x)最大。以此类推。

解释了就算函数有max，也可以求微分。那就接着解这个式子。

也就是交替的用梯度下降训练G和D。G0得到D0*，对G做微分，得到G1，G1得到D1*，对G做微分，得到G2…

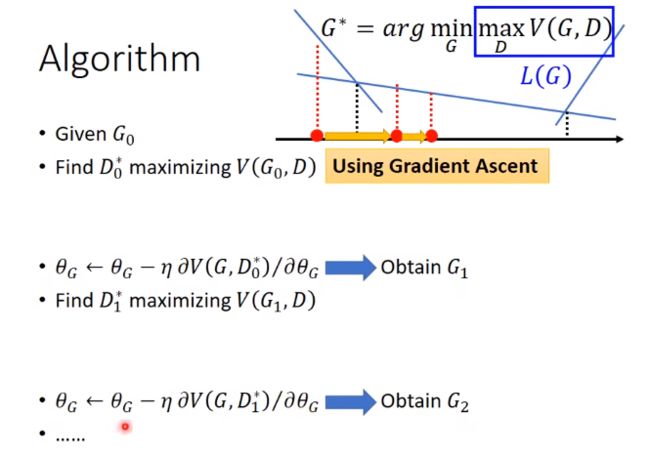
可以看到，这整个过程和GAN是一模一样的。每一步背后的含义是什么呢？就是最小化JS散度。

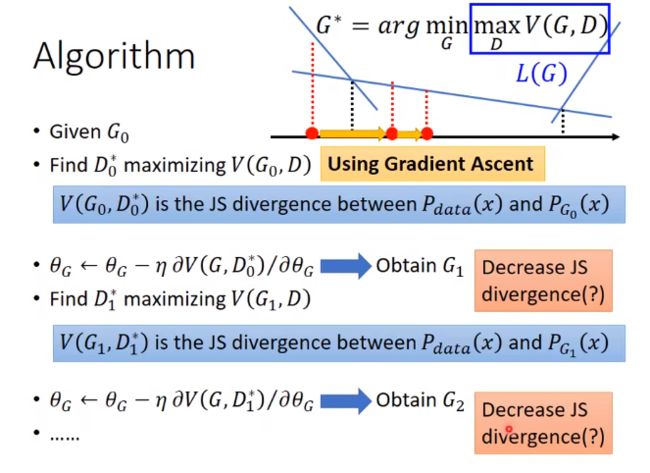
但是上图中的JS散度后面打了个问号，是什么意思呢？
因为这件事情未必等同于在最小化JS散度。
因为G在不断的更新，比如在G0时，D0*得到的maxV，更新到G1时，不一定还是maxV。

那为什么我们又说这个过程是在最小化JS散度？
因为每次更新都是很小的一步，所以我们假设更新后的式子和原来的式子还是非常像的。

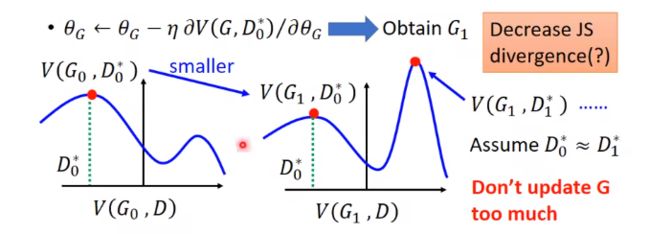
Tip：
所以在训GAN时，G每次更新的不能太多，理论上训D的时候要更多的迭代次数来训到底，找到最大V，才是在量散度，而训G不需要太多次的迭代，如果训太多次，D就无法量散度。

实际训练

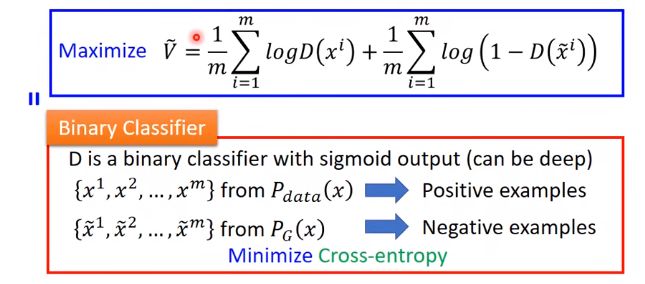
目标函数：

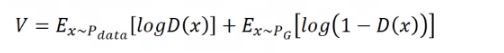
计算该式，要求期望，实际上没有办法真算期望，就用sample代替。

这个式子就等同于训一个二分类器，是一个logistic regression逻辑回归，就是它的输出接了一个sigmoid，是介于0到1之间。
就等同于max V，两个框里的内容等价。

总结：
训D：量散度
训G：最小化散度

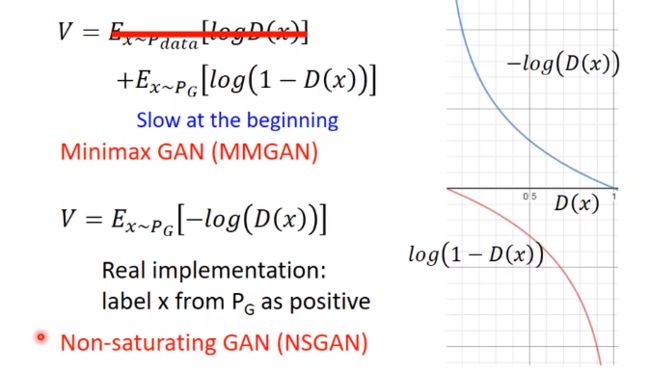
对于G来说，第一项和G无关，所以红线划掉，只剩后半部分，在真实操作中，后面的1也去掉了。这两个函数的趋势是一样的 ，但斜率不同，后面发现都训的起来，差不多。

直观理解GAN

G和D之间的关系是什么样子的呢？
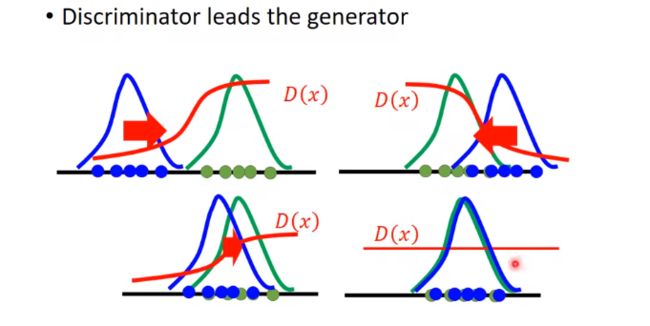
假设绿色是真实数据的分布，蓝色是G生成的数据的分布，现在要训一个D，给绿色较高的分数，给蓝色较低的分数。D的目标函数的值就是这两堆数据的某个散度值。

G会希望D给它生成的数据打高分，所以蓝色就往接近绿色的分布移动一点，但可能一下跑太多了，跑动绿色右边去了，但没关系，再训一次D，D的loss会比较大，说明这两堆数据的散度是比较小的。然后这些点又顺着梯度给的方向往左移，最后蓝色的分布就和绿色分布越来越近，让D分辨不出，最后D会坏掉。

代码

基于pytorch的

import argparse
import os
import numpy as np
import math
 
import torchvision.transforms as transforms
from torchvision.utils import save_image
 
from torch.utils.data import DataLoader
from torchvision import datasets
from torch.autograd import Variable
 
import torch.nn as nn
import torch.nn.functional as F
import torch
 
os.makedirs("images", exist_ok=True)
 
parser = argparse.ArgumentParser()
parser.add_argument("--n_epochs", type=int, default=200, help="number of epochs of training")
parser.add_argument("--batch_size", type=int, default=64, help="size of the batches")
parser.add_argument("--lr", type=float, default=0.0002, help="adam: learning rate")
parser.add_argument("--b1", type=float, default=0.5, help="adam: decay of first order momentum of gradient")
parser.add_argument("--b2", type=float, default=0.999, help="adam: decay of first order momentum of gradient")
parser.add_argument("--n_cpu", type=int, default=8, help="number of cpu threads to use during batch generation")
# 生成原始噪点数据大小--latent_dim
parser.add_argument("--latent_dim", type=int, default=100, help="dimensionality of the latent space")
parser.add_argument("--img_size", type=int, default=28, help="size of each image dimension")
parser.add_argument("--channels", type=int, default=1, help="number of image channels")
parser.add_argument("--sample_interval", type=int, default=500, help="interval betwen image samples")
opt = parser.parse_args()
print(opt)
 
img_shape = (opt.channels, opt.img_size, opt.img_size)
# print(img_shape) 1 ,28,28
# print(int(np.prod(img_shape))) 784
cuda = True if torch.cuda.is_available() else False
 
 
# 生成器模型
class Generator(nn.Module):
    def __init__(self):
        super(Generator, self).__init__()
 
        # 参数 进入32 出来 64  归一化
        def block(in_feat, out_feat, normalize=True):
            # 对传入数据应用线性转换（输入节点数，输出节点数）
            layers = [nn.Linear(in_feat, out_feat)]
            if normalize:
                # 批规范化
                layers.append(nn.BatchNorm1d(out_feat, 0.8))
                # 激活函数
            layers.append(nn.LeakyReLU(0.2, inplace=True))
            return layers
 
        # 模型定义
        self.model = nn.Sequential(
 
            *block(opt.latent_dim, 128, normalize=False),
 
            *block(128, 256),
            *block(256, 512),
            *block(512, 1024),
            # np.prod 用来计算所有元素的乘积
            nn.Linear(1024, int(np.prod(img_shape))),
            nn.Tanh()
        )
 
    # 正向传播
    def forward(self, z):
        img = self.model(z)  # shape 64 784
        img = img.view(img.size(0), *img_shape)  # 64 1 28 28
        return img
 
 
# 判别模型
class Discriminator(nn.Module):
    def __init__(self):
        super(Discriminator, self).__init__()
 
        self.model = nn.Sequential(
            nn.Linear(int(np.prod(img_shape)), 512),
            nn.LeakyReLU(0.2, inplace=True),
            nn.Linear(512, 256),
            nn.LeakyReLU(0.2, inplace=True),
            nn.Linear(256, 1),
            nn.Sigmoid(),
        )
 
    def forward(self, img):
        img_flat = img.view(img.size(0), -1)  # 64 1 28 28 =>64 784
        validity = self.model(img_flat)  # 64 784 =>64 1
 
        return validity
 
 
# Loss function 类似 目标值-得到值 的差值一种运算
adversarial_loss = torch.nn.BCELoss()
 
# Initialize generator and discriminator
generator = Generator()
discriminator = Discriminator()
 
# 如果有gpu
if cuda:
    generator.cuda()
    discriminator.cuda()
    adversarial_loss.cuda()
 
# Configure data loader
os.makedirs("./data/mnist", exist_ok=True)
print(opt.img_size)
dataloader = torch.utils.data.DataLoader(
    datasets.MNIST(
        "./data/mnist",
        train=True,
        download=True,
        transform=transforms.Compose(
            # 其他地方也许是Resize((opt.img_size,opt.img_size)) 也就是（(28,28)）因为后续重塑格式类似于（64，1，28，28）
            # 这里是（28）  后面重塑格式类似于（64，1，28*28）
            # transforms.Normalize([0.5], [0.5])  这是单通道数据集
            # transforms.Normalize((0.5,0.5,0.5), (0.5),(0.5),(0.5))  三通道数据集
            # 图片三个通道
            # 前一个(0.5,0.5,0.5)是设置的mean值 后一个(0.5,0.5,0.5)是是设置各通道的标准差
            # 其作用就是先将输入归一化到(0,1)，再使用公式”(x-mean)/std”，将每个元素分布到(-1,1)
            [transforms.Resize(opt.img_size), transforms.ToTensor(), transforms.Normalize([0.5], [0.5])]
        ),
    ),
    # 一次多少个处理，小图片一般64个
    batch_size=opt.batch_size,
    # 数据集打乱，洗牌
    shuffle=True,
)
 
# Optimizers 优化器
# lr=opt.lr学习率
# betas (Tuple[float, float]，可选):用于计算的系数
# 梯度及其平方的运行平均值(默认值:(0.9,0.999))
optimizer_G = torch.optim.Adam(generator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
optimizer_D = torch.optim.Adam(discriminator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
 
# 判断是否有gpu
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor
 
# ----------
#  Training
# ----------
 
for epoch in range(opt.n_epochs):
    # dataloader中的数据是一张图片对应一个标签，所以imgs对应的是图片，_对应的是标签，而i是enumerate输出的功能
    for i, (imgs, _) in enumerate(dataloader):
 
        # Adversarial ground truths
        # 这部分定义的相当于是一个标准，vaild可以想象成是64行1列的向量，就是为了在后面计算损失时，和1比较；fake也是一样是全为0的向量，用法和1的用法相同。
        valid = Variable(Tensor(imgs.size(0), 1).fill_(1.0), requires_grad=False)
        fake = Variable(Tensor(imgs.size(0), 1).fill_(0.0), requires_grad=False)
 
        # Configure input
        # 这句是将真实的图片转化为神经网络可以处理的变量。变为Tensor
        # print(type(imgs)) Tensor
        real_imgs = Variable(imgs.type(Tensor))
        # print(type(real_imgs)) Tensor
        # -----------------
        #  Train Generator
        # -----------------
 
        # optimizer.zero_grad()意思是把梯度置零
        # 每次的训练之前都将上一次的梯度置为零，以避免上一次的梯度的干扰
        optimizer_G.zero_grad()
 
        # Sample noise as generator input
        # 这部分就是在上面训练生成网络的z的输入值，np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim)的意思就是
        # 64个噪音（基础值为100大小的） 0，代表正态分布的均值，1，代表正态分布的方差
        z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
        # Generate a batch of images 返回一个批次即64个
        gen_imgs = generator(z)
 
        # Loss measures generator's ability to fool the discriminator
        # 计算这64个图片总损失  生成器损失
        g_loss = adversarial_loss(discriminator(gen_imgs), valid)
        # 反向传播
        g_loss.backward()
        optimizer_G.step()
        # ---------------------
        #  Train Discriminator
        # ---------------------
        # 梯度清零
        optimizer_D.zero_grad()
        # Measure discriminator's ability to classify real from generated samples
        # 判别器判别真实图片是真的的损失
        real_loss = adversarial_loss(discriminator(real_imgs), valid)
        # 判别器判别假的图片是假的的损失
        fake_loss = adversarial_loss(discriminator(gen_imgs.detach()), fake)
        # 判别器去判别真实图片是真的的概率大，并且判别假图片是真的的概率小，说明判别器越准确所以说是maxD，
        # 生成器就是想生成真实的图片来迷惑判别器，所以理论上想让生成器生成真实的图片概率大，
        # 由于公式第二部分表示生成器的损失，G（z）前有个负号，所以如果结果小则证明G生成的越真实，所以说minG
        d_loss = (real_loss + fake_loss) / 2
 
        # 反向传播
        d_loss.backward()
        optimizer_D.step()
 
        print(
            "[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]"
            % (epoch, opt.n_epochs, i, len(dataloader), d_loss.item(), g_loss.item())
        )
 
        batches_done = epoch * len(dataloader) + i
        if batches_done % opt.sample_interval == 0:
            save_image(gen_imgs.data[:25], "images/%d.png" % batches_done, nrow=5, normalize=True)