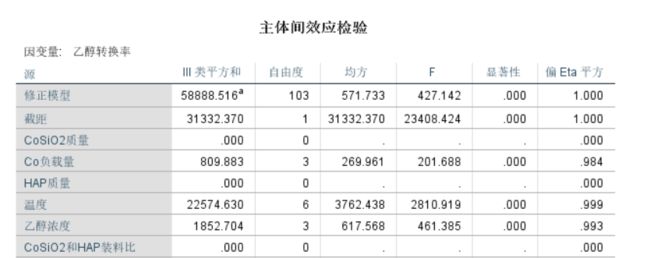
2021年数模国赛B题--乙醇偶合制备 C4 烯烃
一.题目
C4 烯烃广泛应用于化工产品及医药的生产,乙醇是生产制备 C4 烯烃的原料。在制备过程中,催化剂组合(即:Co 负载量、Co/SiO2 和 HAP 装料比、乙醇浓度的组合)与温度对 C4 烯烃的选择性和 C4 烯烃收率将产生影响(名词解释见附录)。因此通过对催化剂组合设计,探索乙醇催化偶合制备 C4 烯烃的工艺条件具有非常重要的意义和价值。
某化工实验室针对不同催化剂在不同温度下做了一系列实验,结果如附件 1 和附件 2 所示。请通过数学建模完成下列问题:
(1) 对附件 1 中每种催化剂组合,分别研究乙醇转化率、C4 烯烃的选择性与温度的关系,并对附件 2 中 350 度时给定的催化剂组合在一次实验不同时间的测试结果进行分析。
(2) 探讨不同催化剂组合及温度对乙醇转化率以及 C4 烯烃选择性大小的影响。
(3) 如何选择催化剂组合与温度,使得在相同实验条件下 C4 烯烃收率尽可能高。若使温度低于 350 度,又如何选择催化剂组合与温度,使得 C4 烯烃收率尽可能高。
(4) 如果允许再增加 5 次实验,应如何设计,并给出详细理由。
二.题目求解(主要编程部分)
1.问题一
(1)数据可视化处理:画出散点图
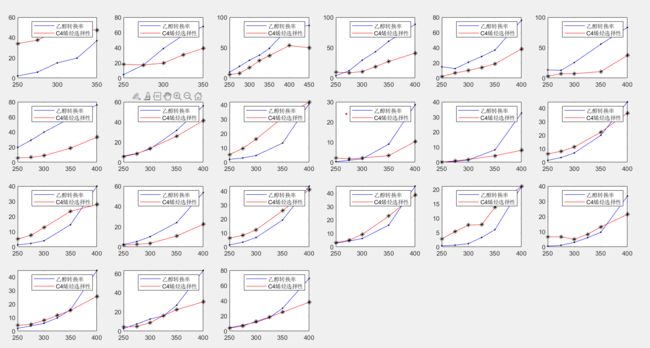
(2)研究乙醇转化率、C4 烯烃的选择性与温度的关系
乙醇转换率是化学变化,最大100%,最多维持在100%
因此建立 Logistic 模型对数据进行拟合。
x= -xm/(exp(log(1 - xm/x0) - r*t) - 1)
此处拟合方法:
(1)使用fit函数拟合
(2)使用lsqcurvefit函数拟合
(3)使用cftool工具箱拟合
注意由于出现e的负T次方,T(温度)可以到达300,所以会出现值为0,这里对T进行处理减去240
最后通过R^2检验拟合程度的好坏
c4烯烃选择性使用二次曲线拟合即可(参数不要过多,不要超过三个,否则可能出现过拟合情况)
350 度时给定的催化剂组合在一次实验不同时间的测试结果同样使用二次曲线拟合即可
可以先对 乙醇转换率和C4烯烃选择性和温度进行相关性分析
两个变量是线性关系才能使用皮尔逊相关系数,因此这里采用斯皮尔曼相关系数
1.连续数据,正态分布,线性关系,用pearson相关系数是最恰当,当然用spearman相关系数也可以, 就是效率没有pearson相关系数高。
2.上述任一条件不满足,就用spearman相关系数,不能用pearson相关系数。
之后使用cftool工具箱进行多项式拟合
clc;clear;close all
tic
%% 读取数据
zhuanhuan=xlsread('附件1.xlsx','D2:D115');
xuanze=xlsread('附件1.xlsx','F2:F115');
temp=xlsread('附件1.xlsx','C2:C115');
time=xlsread('附件2.xlsx','A4:A10');
other=xlsread('附件2.xlsx','B4:H10');
%% 数据分类和画图
A=[]; %转换率
W=[]; %温度
X=[]; %选择性
e=[]; %系数
for i=1:2
A=[A;zhuanhuan(5*i-4:5*i)];
W=[W;temp(5*i-4:5*i)];
X=[X;xuanze(5*i-4:5*i)];
temp2=W(5*i-4:5*i)-240; Change=A(5*i-4:5*i); subplot(4,6,i);
plot(temp2,Change,'b'); hold on; plot(temp2,Change,'k.','HandleVisibility','off'); %温度和转换率
hold on
plot(temp2,X(5*i-4:5*i),'r');hold on; plot(temp2,X(5*i-4:5*i),'k.','HandleVisibility','off'); %温度和选择性
legend('乙醇转换率','C4烯烃选择性')
%% 方法一
% g=@(N,r,x) N./(1+(N/W(5*i-4)-1).*exp(-r*x)); %要用点除会有矩阵运算
% g=fittype(g);
% [f{i},r{i}]=fit(temp2,Change,g,'StartPoint',rand(1,2)); %系数有几个变量就定义几个变量,自变量一定要是x
%% 方法二
% g=@(c,x) c(1)./(1+(c(1)/W(5*i-4)-1)*exp(-c(2)*x)); %要用点除会有矩阵运算
% e=[e;lsqcurvefit(g,[150,0.15],temp2,Change)]; %函数句柄只能有两个变量,前一个是拟合系数后一个是自变量
% [e,r]=lsqcurvefit(g,rand(1,2),temp2,Change) %函数句柄只能有两个变量,前一个是拟合系数后一个是自变量
[xishu{i},r2(i)]=polyfit(W(5*i-4:5*i),X(5*i-4:5*i),2);
%% 方法三(先对数据分类)
namestr1 = ['C' num2str(i) '=A(5*i-4:5*i)'];
eval(namestr1);
namestr2 = ['T' num2str(i) '=W(5*i-4:5*i)'];
eval(namestr2);
end
A=[A;zhuanhuan(11:17)];
W=[W;temp(11:17)];
X=[X;xuanze(11:17)];
subplot(4,6,3);
plot(W(11:17),A(11:17),'b'); hold on; plot(W(11:17),A(11:17),'k.','HandleVisibility','off'); %温度和转换率
hold on
plot(W(11:17),X(11:17),'r');hold on; plot(W(11:17),X(11:17),'k.','HandleVisibility','off'); %温度和选择性
legend('乙醇转换率','C4烯烃选择性')
g=@(N,r,x) N./(1+(N/W(11)-1).*exp(-r*x));
g=fittype(g);
f{3}=fit(temp2,Change,g,'StartPoint',rand(1,2));
for i=4:5
A=[A;zhuanhuan(6*(i-1):6*i-1)];
W=[W;temp(6*(i-1):6*i-1)];
X=[X;xuanze(6*(i-1):6*i-1)];
subplot(4,6,i);
plot(W(6*(i-1):6*i-1),A(6*(i-1):6*i-1),'b'); hold on; plot(W(6*(i-1):6*i-1),A(6*(i-1):6*i-1),'k.','HandleVisibility','off'); %温度和转换率
hold on
plot(W(6*(i-1):6*i-1),X(6*(i-1):6*i-1),'r');hold on; plot(W(6*(i-1):6*i-1),X(6*(i-1):6*i-1),'k.','HandleVisibility','off'); %温度和选择性
legend('乙醇转换率','C4烯烃选择性')
g=@(N,r,x) N./(1+(N/W(5*i-4)-1).*exp(-r*x));
g=fittype(g);
f{i}=fit(temp2,Change,g,'StartPoint',rand(1,2));
end
for i=6:16
A=[A;zhuanhuan(5*i:5*(i+1)-1)];
W=[W;temp(5*i:5*i+4)];
X=[X;xuanze(5*i:5*i+4)];
subplot(4,6,i);
plot(W(5*i:5*(i+1)-1),A(5*i:5*(i+1)-1),'b'); hold on; plot(W(5*i:5*(i+1)-1),A(5*i:5*(i+1)-1),'k.','HandleVisibility','off'); %温度和转换率
hold on
plot(W(5*i:5*(i+1)-1),X(5*i:5*(i+1)-1),'r'); hold on; plot(W(5*i:5*(i+1)-1),X(5*i:5*(i+1)-1),'k.','HandleVisibility','off'); %温度和选择性
legend('乙醇转换率','C4烯烃选择性')
g=@(N,r,x) N./(1+(N/W(5*i-4)-1).*exp(-r*x));
g=fittype(g);
f{i}=fit(temp2,Change,g,'StartPoint',rand(1,2));
end
for i=17:21
A=[A;zhuanhuan(6*(i-3)+1:6*(i-2))];
W=[W;temp(6*(i-3)+1:6*(i-2))];
X=[X;xuanze(6*(i-3)+1:6*(i-2))];
subplot(4,6,i);
plot(W(6*(i-3)+1:6*(i-2)),A(6*(i-3)+1:6*(i-2)),'b'); hold on; plot(W(6*(i-3)+1:6*(i-2)),A(6*(i-3)+1:6*(i-2)),'k.','HandleVisibility','off'); %温度和转换率
hold on
plot(W(6*(i-3)+1:6*(i-2)),X(6*(i-3)+1:6*(i-2)),'r'); hold on; plot(W(6*(i-3)+1:6*(i-2)),X(6*(i-3)+1:6*(i-2)),'k.','HandleVisibility','off'); %温度和选择性
legend('乙醇转换率','C4烯烃选择性')
g=@(N,r,x) N./(1+(N/W(5*i-4)-1).*exp(-r*x));
g=fittype(g);
f{i}=fit(temp2,Change,g,'StartPoint',rand(1,2));
end
%% 阻滞增长模型(logistic模型)
x = dsolve('Dx=r*(1-x/xm)*x','x(0)=2.07','t');
%% 附件2数据处理
figure(2)
y1=other(:,1);
plot(time,y1); hold on; plot(time,y1,'bo','MarkerFaceColor','r');
%二次拟合同上,不想写了,偷个懒
toc
2.问题二
使用多元线性回归分析
步骤:
(1)确定自变量,因变量进行描述性统计
(2)OLS回归
(3)异方差检验:怀特检验
(4)多重共线性检验:如果有进行逐步回归
步骤一
首先对数据分类(使用excel表格对数据进行填充,同时删除A11)
步骤二
描述性统计
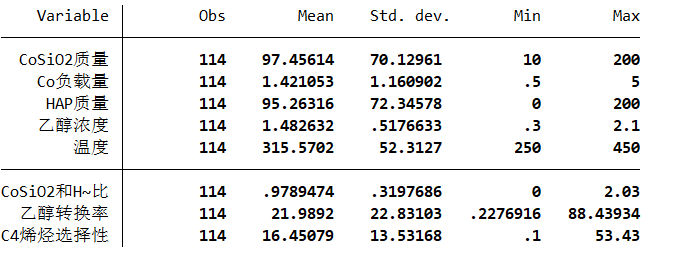
OLS回归
分别对乙醇转换率和C4烯烃选择性进行回归分析
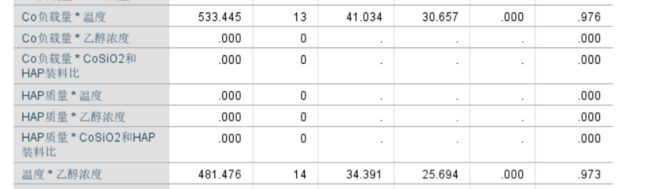
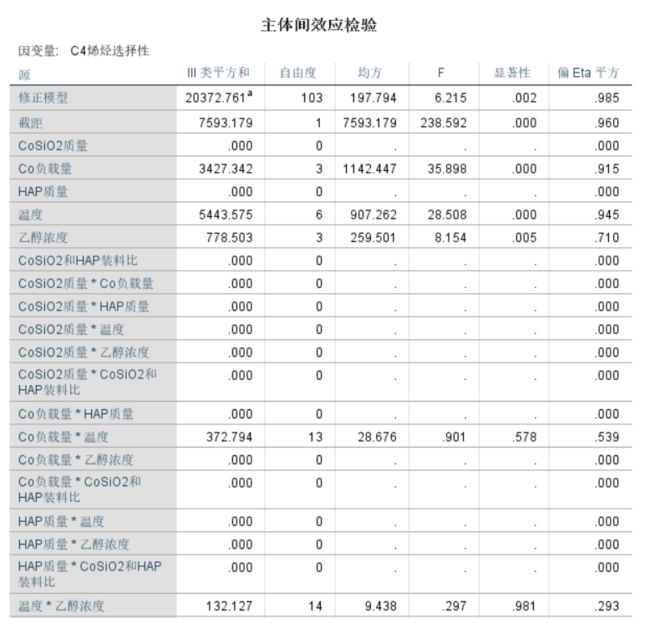
(第一列从上到下分别是:SSR SSE SST ,df 是自由度,表格其实就是方差分析表)

得到的联合显著性检验p值<0.05,因此在95%的置信区间下,拒绝原假设,认为线性回归前面系数不全为0,模型成立
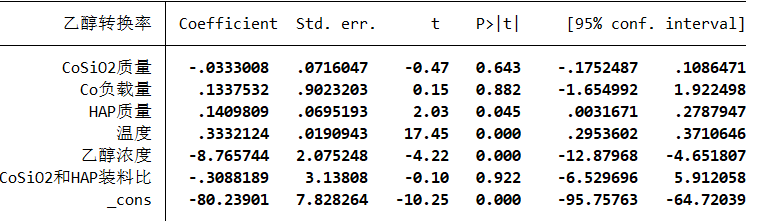
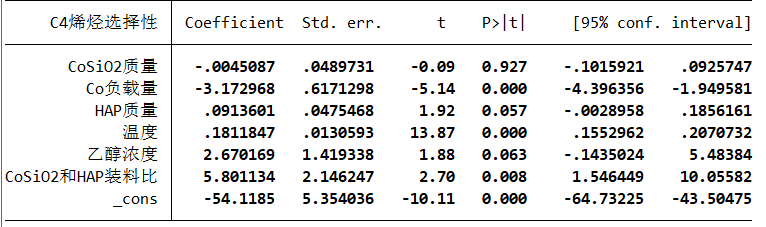
对回归系数进行显著性t检验,发现有几个变量不显著,所以OLS模型并不满足要求,接下来进行异方差检验和多重共线性检验
步骤三
异方差检验:
多重共线性检验:
计算方差膨胀因子:都是小于10
所以不存在多重共线性
步骤四
逐步回归:
解决显著性检验问题
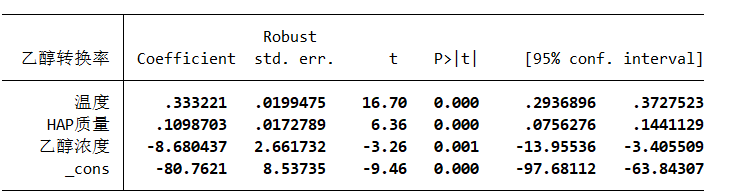
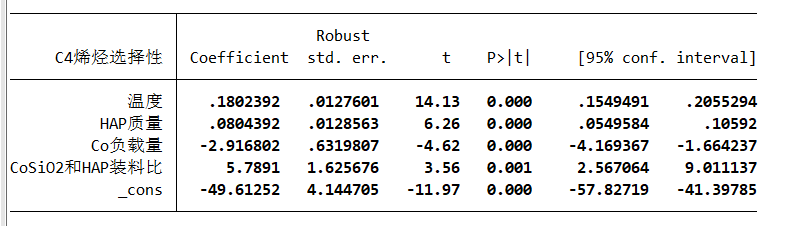
但是这样删除变量可能会引起内生性问题导致估计系数有偏,同时缺少了变量,接下来进行改进
方法二:
首先对数据标准化,方便研究之后每个系数所占的权重
看计量经济学书,面板数据这里也没有说必须要要标准化;
同时,可以查查国际英文的期刊,做面板分析的,有多少文章是用标准化的数据的?如果用了,是怎么用的?
引入交互项
六个自变量之间可能两两之间相互影响

通过逐步回归:
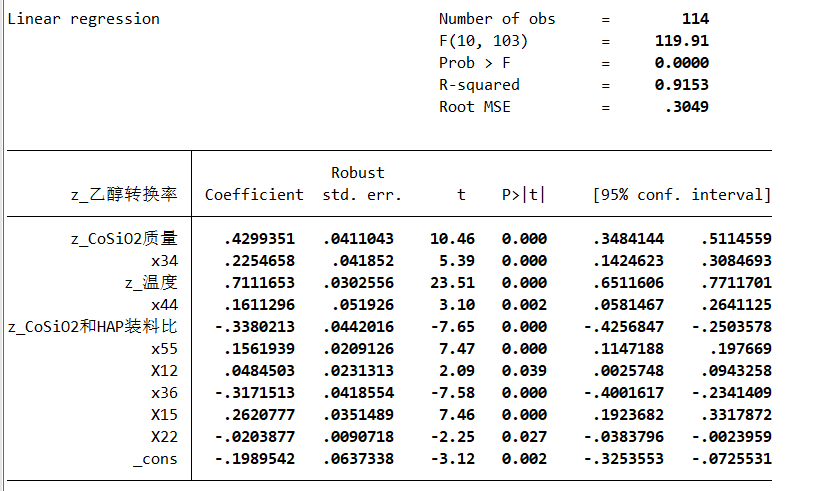
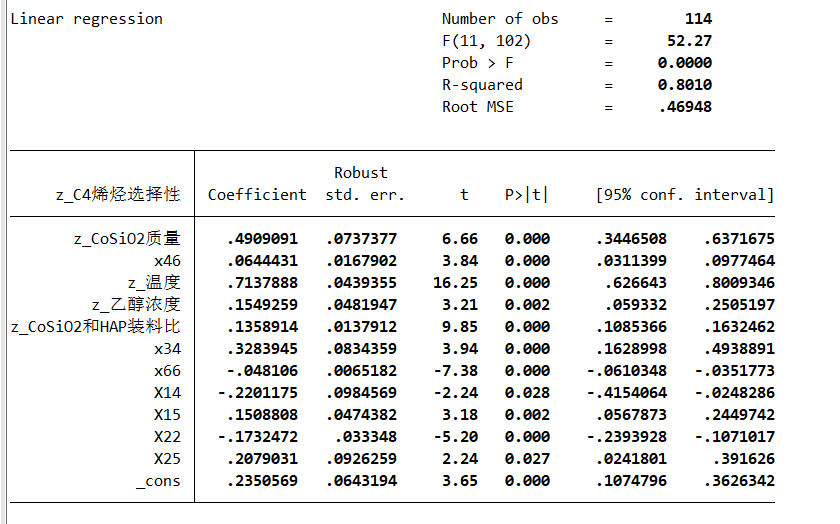
这样可以得到包含到所有变量。同时R2都超过了80%拟合效果较好
通过标准回归系数知道温度对乙醇转换率影响最大
stata相关代码
summarize 变量 //描述性统计
stepwise 变量,r pr(0.05) //逐步回归
// 异方差BP检验
estat hettest ,rhs iid
// 异方差怀特检验
estat imtest,white
// 使用OLS + 稳健的标准误
regress 变量, r
// 计算VIF
estat vif
// 作评价量的概率密度估计图
kdensity 评价量
// Stata会自动剔除多重共线性的变量
3. 问题三
C4 烯烃收率:其值为乙醇转化率 * C4 烯烃的选择性。
题目求最大值问题,即规划问题,首先要求出目标函数,可以将因变量设置为乙醇转化率 * C4 烯烃的选择性,再进行多元回归分析
目标函数求解整体思路同问题二
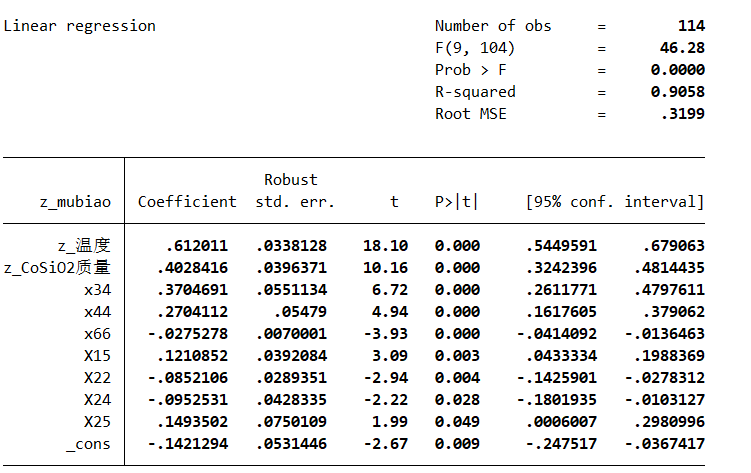
约束条件:

使用lingo求解,这里对约束条件也要进行标准化处理
问题五(略)
自用学习使用