HoudiniVex笔记_P22_RemappingBasics重映射
原视频：https://www.youtube.com/playlist?list=PLzRzqTjuGIDhiXsP0hN3qBxAZ6lkVfGDI
Bili：Houdini最强VEX算法教程 - VEX for Algorithmic Design_哔哩哔哩_bilibili
Houdini版本：19.5
1、fit函数
取范围(omin，omax)中的值，并将其映射到新范围(nmin，nmax)中的相应值。
2、fit01函数
如果(omin，omax)值范围是(0~1)，可直接使用fit01函数将其映射到新范围(nmin，nmax)中。
3、fit10函数
与fit01相似，只不过(omin，omax)值范围是(1~0)。当然，直接使用fit01函数，改变(nmin，nmax)能达到同样的效果。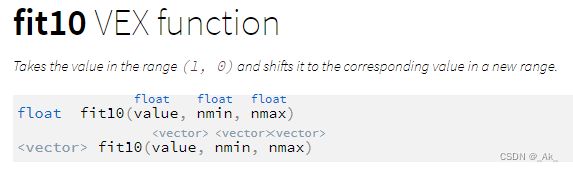
4、fit11函数
取范围（-1，1）中的值，并将其移动到新范围（nmin，nmax）中的相应值。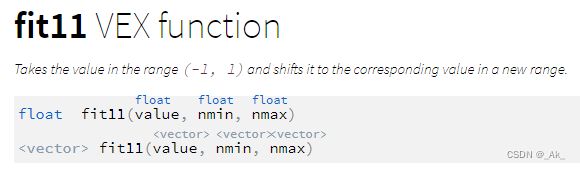
5、efit函数
取范围(omin，omax)中的值，并将其移动到新范围(nmin，nmax)中的相应值。与fit不同，函数不会将value值钳制在给定范围内。多与三角函数/角度值等结合使用。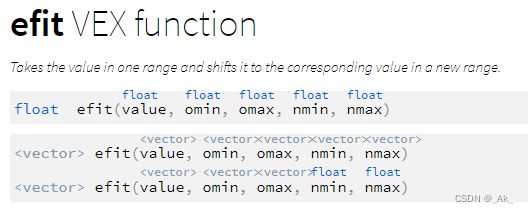
6、Exercise—重映射与噪波
记录下。
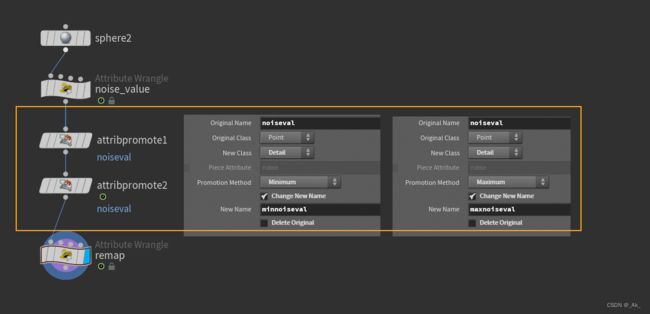
eg.先上结果，（scale==1.5）（min_height==-0.5，max_height==0.5）
①节点连接及设置，
②完整代码如下，
//noise_value节点
vector pos = @P * chf('scale');
vector4 seed = set(pos.x, pos.y, pos.z, @Time);
float noiseval = noise(seed);
f@noiseval = noiseval;//remap节点
float minval = detail(0, 'minnoiseval');
float maxval = detail(0, 'maxnoiseval');
float minheight = chf('min_height');
float maxheight = chf('max_height');
float height = fit(f@noiseval, minval, maxval, minheight, maxheight);
@P += @N * height;7、Exercise—重映射与距离
对模型搞个大波浪（三角函数周期与映射）。
surfacedist() 函数：返回点与模型的最近距离
理论：
①在空间中添加随意点，根据模型与该点的距离进行上色，
②加上efit函数，可是其表面颜色呈周期性变化（一圈又一圈），
操作：
①节点设置如下，
②类型为Points的ripple_surface节点代码如下，
vector npos = point(1, 'P', 0);
int npt = nearpoint(0, npos);
int closest = -1; //模型上最近距离点的点号@ptnum
float dist = surfacedist(0, itoa(npt), 'P', @ptnum, closest, 'surface'); //点与模型的距离
float ang =efit(dist, 0.0, chf('rangdsit'), 0, $PI * 2.0) - @Time*5;
float val = sin(ang);
float height = fit11(val, chf('tmin'), chf('tmax'));
float col = fit11(val, 0.0, 1.0); //col值呈sin函数周期变化
@P += @N * height; //沿法线偏移
f@dist = dist * col;8、Ramp斜坡重映射函数/参数
可以看看这篇笔记：
【HoudiniVex笔记_P3_ParameterBase参数基础】的第四部分。
感兴趣可以继续看视频部分【1h7m ~ 1h17m】。
9、重映射与插值/Lerp
仅截图记录下——>小球从一个形态平滑过渡到另一个形态。
10、Exercise—重映射与插值/Lerp
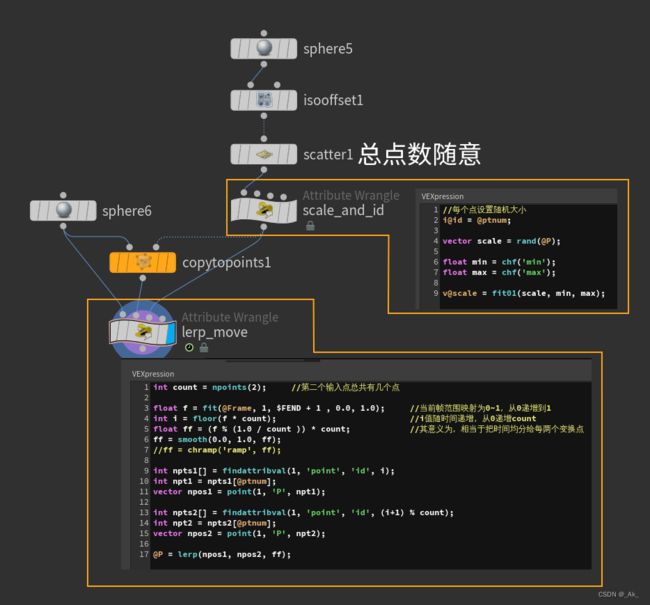
上一节是两小球之间的变化过渡。这次是多个小球之间的形态变化过渡。
仅大概记录下，感兴趣的可以跟做下，
//每个点设置随机大小
i@id = @ptnum;
vector scale = rand(@P);
float min = chf('min');
float max = chf('max');
v@scale = fit01(scale, min, max);int count = npoints(2); //第二个输入点总共有几个点
float f = fit(@Frame, 1, $FEND + 1 , 0.0, 1.0); //当前帧范围映射为0~1，从0递增到1
int i = floor(f * count); //i值随时间递增，从0递增count
float ff = (f % (1.0 / count )) * count; //其意义为，相当于把时间均分给每两个变换点
ff = smooth(0.0, 1.0, ff);
//ff = chramp('ramp', ff);
int npts1[] = findattribval(1, 'point', 'id', i);
int npt1 = npts1[@ptnum];
vector npos1 = point(1, 'P', npt1);
int npts2[] = findattribval(1, 'point', 'id', (i+1) % count);
int npt2 = npts2[@ptnum];
vector npos2 = point(1, 'P', npt2);
@P = lerp(npos1, npos2, ff);11、重映射与UV
展UV，记录下。
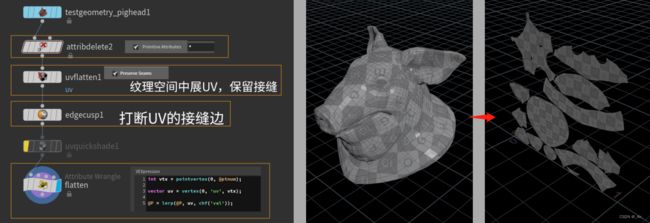
12、 Exercise—重映射与UV
记录下，感兴趣可以跟着做做。
int vtx = pointvertex(0, @ptnum);
vector uv = vertex(0, 'uv', vtx);
float x = chf('x');
float y = chf('y');
//相当于划分成一块块
uv = uv % set(x, y, 1.0);
uv = fit(uv, set(0,0,0), set(x, y, 0), set(0,0,0), set(1,1,1));
// 也可这样写 uv = uv * set(1/x, 1/y, 1.0);
uv *= $PI;
float xh = sin(uv.x);
float yh = sin(uv.y);
@P += @N * (xh * yh) * chf('height');