几种图灵斑(Turing Patterns)的简单matlab演示(BZ反应、Gray-Scott模型、LE模型)
几种图灵斑(Turing Patterns)的简单matlab演示(BZ反应、Gray-Scott模型、LE模型)
- 0 引言
- 1 BZ震荡反应
- 2 Gray Scott模型
- 3 LE模型(CIMA反应)
惯例声明:本人没有相关的工程应用经验,只是纯粹对相关算法感兴趣才写此博客。所以如果有错误,欢迎在评论区指正,不胜感激。本文主要关注于算法的实现,对于实际应用等问题本人没有任何经验,所以也不再涉及。
0 引言
1952年艾伦·图灵在他的论文中the chemical basisof morphogenesis(形态发生的化学基础)中,给出图灵斑图的大概概念,从数学和化学的角度,揭示了生物体表面斑纹的产生机理。
这种图灵斑图产生机理是一种反应-扩散体系,之后在多种生物、化学、地理等学科被观测到,可以说是一种遍布于大自然的普适性的规律。
本文以三种经典模型为例,介绍图灵斑图的matlab数值仿真方法。由于本人不是相关领域的研究人员,所以主要注重于数值计算方面,而不涉及图灵斑图相关的化学反应机理、非线性分岔等。
相关参考资料如下:
[1] Morphology of Experimental and Simulated Turing Patterns (2009)
[2] Simulating the Belousov-Zhabotinsky reaction (2017) https://scipython.com/blog/simulating-the-belousov-zhabotinsky-reaction/
[3] 一个演示Gray–Scott model的网址: http://www.karlsims.com/rdtool.html
建议用Chrome浏览器打开
[4]matlab区域填充_图灵斑图与反应扩散方程——Matlab的实现
https://blog.csdn.net/weixin_30278943/article/details/112067158
[5] The Lengyel–Epstein Reaction Diffusion System (2020)
[6] Machine learning with Patterns based on Lengyel-Epstein model
https://github.com/standing-o/Machine-learning_with_Patterns_based_on_Lengyel-Epstein_model
[7] 混乱博物馆-图灵斑图:生命图案的奥秘 https://zhuanlan.zhihu.com/p/29118927
[8] Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation (2010)
[9] Gray-Scott-Complex Patterns in a Simple System (1993)
[10] 一类离散反应扩散捕食系统的分岔和斑图自组织研究(杨洪举)
列的东西杂七杂八的,毕竟也不是啥正经论文,大概按照重要性顺序列了一下。
下面举的图灵斑仿真例子,实际上就是求解某个数学方程的解。所以下面代码需要有简单的数值分析基础,只要知道如何简单离散解偏微分方程就可以。数值方法后文中也会稍微有所涉及,但不会太详细。
1 BZ震荡反应
BZ反应是在1958年由Belousov和Zhabotinski发现而得名。
模型可以简单被写为下面三个方程:
A + B → 2 A B + C → 2 B C + A → 2 C A+B\to2A \\ B+C\to2B \\ C+A\to2C \\ A+B→2AB+C→2BC+A→2C
每个量下一时刻的值,会随上一时刻的变量而改变,可以被写作:
A t + 1 = A t + A t ( α B t − γ C t ) B t + 1 = B t + B t ( β C t − α A t ) C t + 1 = C t + C t ( α A t − β B t ) A_{t+1}=A_t+A_t (\alpha B_t-\gamma C_t) \\ B_{t+1}=B_t+B_t (\beta C_t-\alpha A_t) \\ C_{t+1}=C_t+C_t (\alpha A_t-\beta B_t) \\ At+1=At+At(αBt−γCt)Bt+1=Bt+Bt(βCt−αAt)Ct+1=Ct+Ct(αAt−βBt)
这里取常数 α = 1.2 \alpha=1.2 α=1.2, β = 1 \beta=1 β=1, γ = 1 \gamma=1 γ=1。
且为了模拟反应扩散,下一步计算时,还需要对该变量取周围8个变量取平均,作为当前网格点的值。在matlab里,用imfilter函数来实现。
初始值定义为0~1之前的随机数。
代码如下:
clear
clc
close all
% Belousov-Zhabotinsky反应
%构建网格
dt=0.5;%时间步长
N=500;%网格总数量
dx=1;%网格大小
x=dx*(1:N);
[X,Y]=meshgrid(x,x);
%初始化,采用随机初始化
A0=rand(size(X));
B0=rand(size(X));
C0=rand(size(X));
%方程初常数
alpha=1.2;
beta=1;
gamma=1;
%微分方程求解
F=ones(3)/8;F(2,2)=0;
A_Old=A0;
B_Old=B0;
C_Old=C0;
for k_t=1:600
%模拟扩散项
A_Old=imfilter(A_Old,F,'circular');
B_Old=imfilter(B_Old,F,'circular');
C_Old=imfilter(C_Old,F,'circular');
%1阶时间精度
A_New=A_Old+A_Old.*(alpha*B_Old-gamma*C_Old)*dt;
B_New=B_Old+B_Old.*(beta*C_Old -alpha*A_Old)*dt;
C_New=C_Old+C_Old.*(gamma*A_Old- beta*B_Old)*dt;
A_Old=A_New;
B_Old=B_New;
C_Old=C_New;
%绘图
if k_t>50 && mod(k_t,2)==1
figure(1)
clf
pcolor(X,Y,A_New);shading interp
caxis([0,1])
pause(0.01)
end
end
可以看到BZ震荡反应典型的两个图案:震荡和螺旋。
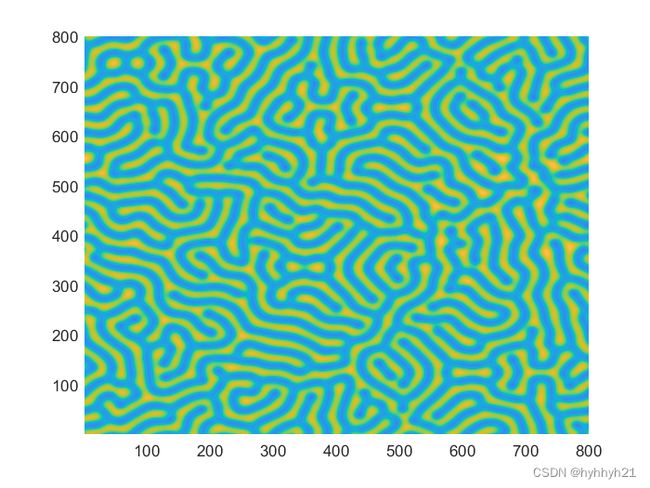
2 Gray Scott模型
Gray Scott模型是一种典型的反应扩散系统。其方程可以写作:
U + 2 V → 3 V V → P U+2V \to 3V \\ V \to P U+2V→3VV→P
用来计算的微分方程可以写作:
∂ U ∂ t = D U Δ U − U V 2 + F ( 1 − U ) ∂ V ∂ t = D V Δ V + U V 2 − ( F + k ) V \frac{\partial U}{\partial t} =D_U\Delta U-U V^2+F(1-U) \\ ~\\ \frac{\partial V}{\partial t} =D_V\Delta V+U V^2-(F+k)V ∂t∂U=DUΔU−UV2+F(1−U) ∂t∂V=DVΔV+UV2−(F+k)V
前面时间t项,用一阶时间精度计算,即:
∂ U ∂ t = U t + 1 − U t d t \frac{\partial U}{\partial t}=\frac{U_{t+1}-U_t}{dt} ∂t∂U=dtUt+1−Ut
本文研究的是二维xy平面的方程的解,所以后面的拉普帕斯方程展开为:
Δ U = ∇ 2 U = ∂ 2 U ∂ x 2 + ∂ 2 U ∂ y 2 \Delta U=\nabla^2U=\frac{\partial^2 U}{\partial x^2}+\frac{\partial^2 U}{\partial y^2} ΔU=∇2U=∂x2∂2U+∂y2∂2U
这一部分可以离散化,构造出5点差分格式和9点差分格式。其中9点差分格式精度更高,但是计算速度更慢。这里假设网格均匀划分,dx=dy。定义中间 U i , j U_{i,j} Ui,j表示x方向第i个网格,j方向第j个网格,则5点差分格式为:
Δ U = ∂ 2 U ∂ x 2 + ∂ 2 U ∂ y 2 = U i + 1 , j − 2 ∗ U i , j + U i − 1 , j + U i , j + 1 − 2 ∗ U i , j + U i , j − 1 d x 2 \Delta U=\frac{\partial^2 U}{\partial x^2}+\frac{\partial^2 U}{\partial y^2}=\frac{U_{i+1,j}-2*U_{i,j}+U_{i-1,j}+U_{i,j+1}-2*U_{i,j}+U_{i,j-1}}{{dx}^2} ΔU=∂x2∂2U+∂y2∂2U=dx2Ui+1,j−2∗Ui,j+Ui−1,j+Ui,j+1−2∗Ui,j+Ui,j−1
9点差分格式为:
Δ U = − 20 ∗ U i , j + 4 U i + 1 , j + 4 U i − 1 , j + 4 U i , j + 1 + 4 U i , j − 1 6 d x 2 + U i − 1 , j − 1 + U i + 1 , j − 1 + U i − 1 , j + 1 + U i + 1 , j + 1 6 d x 2 \Delta U=\frac{-20*U_{i,j}+4U_{i+1,j}+4U_{i-1,j}+4U_{i,j+1}+4U_{i,j-1}}{{6 dx}^2}\\~\\ +\frac{U_{i-1,j-1}+U_{i+1,j-1}+U_{i-1,j+1}+U_{i+1,j+1}}{{6 dx}^2} ΔU=6dx2−20∗Ui,j+4Ui+1,j+4Ui−1,j+4Ui,j+1+4Ui,j−1 +6dx2Ui−1,j−1+Ui+1,j−1+Ui−1,j+1+Ui+1,j+1
因此最上面的微分方程的离散格式可以写作:
U t + 1 = U t + ( D U U i + 1 , j − 2 ∗ U i , j + U i − 1 , j + U i , j + 1 − 2 ∗ U i , j + U i , j − 1 d x 2 − U V 2 + F ( 1 − U ) ) d t V t + 1 = V t + ( D V V i + 1 , j − 2 ∗ V i , j + V i − 1 , j + V i , j + 1 − 2 ∗ V i , j + V i , j − 1 d x 2 + U V 2 − ( F + k ) V ) d t U_{t+1}=U_{t}+(D_U\frac{U_{i+1,j}-2*U_{i,j}+U_{i-1,j}+U_{i,j+1}-2*U_{i,j}+U_{i,j-1}}{{dx}^2}-U V^2+F(1-U) )dt \\ ~\\ V_{t+1}=V_{t}+(D_V\frac{V_{i+1,j}-2*V_{i,j}+V_{i-1,j}+V_{i,j+1}-2*V_{i,j}+V_{i,j-1}}{{dx}^2}+U V^2-(F+k)V)dt Ut+1=Ut+(DUdx2Ui+1,j−2∗Ui,j+Ui−1,j+Ui,j+1−2∗Ui,j+Ui,j−1−UV2+F(1−U))dt Vt+1=Vt+(DVdx2Vi+1,j−2∗Vi,j+Vi−1,j+Vi,j+1−2∗Vi,j+Vi,j−1+UV2−(F+k)V)dt
接下来是常数、边界、初始值的选取。
常数(理解之前,尽量不要动这些常数):
时间步长dt=0.2,空间网格dx=1
Du=5.0*dt/dx^2
Dv=2.5*dt/dx^2
F=0.0340
k=0.0590
这里F、k的选取,参照http://mrob.com/pub/comp/xmorphia/
边界条件采用循环边界条件,实现方法为,用circshift函数来获取 U i + 1 , j U_{i+1,j} Ui+1,j之类的信息,这样就自然的满足了循环条件。
初始值U=1,V=0。之后随机选取一小部分区域的V设置为1,作为扰动。
clear
clc
close all
% Gray Scott模型
%构建网格
dt=0.1;%时间步长
N=800;%网格总数量
dx=1;%网格大小
x=dx*(1:N);
[X,Y]=meshgrid(x,x);
U0=ones(size(X));
V0=zeros(size(X));
%初始化
for k=1:5
ind1=randi([1,N])+(1:30);
ind2=randi([1,N])+(1:60);
if any(ind1>N) || any(ind2>N)
continue
end
V0( ind1 , ind2 )=1;
V0(V0>1)=1;
end
%方程初常数
Du=5*dt/dx^2;
Dv=2.5*dt/dx^2;
F=0.0340;
k=0.0590;
%微分方程求解
U_Old=U0;
V_Old=V0;
for k_t=1:N*50
%1阶时间精度
U_New=U_Old+(Du*Laplace_Diff5(U_Old,dx)-U_Old.*V_Old.^2+F*(1-U_Old))*dt;
V_New=V_Old+(Dv*Laplace_Diff5(V_Old,dx)+U_Old.*V_Old.^2-(F+k)*V_Old)*dt;
U_Old=U_New;
V_Old=V_New;
%绘图
if mod(k_t,400)==1
figure(1)
clf
pcolor(X,Y,U_New);shading interp
caxis([0,1])
pause(0.01)
end
end
function L = Laplace_Diff5(U,dx)
%5点Laplace差分格式
%U_nn=circshift(U,[1,1]);%U_(i-1,j-1)
U_0n=circshift(U,[1,0]);%U_(i,j-1)
%U_pn=circshift(U,[1,-1]);%U_(i+1,j-1)
U_n0=circshift(U,[0,1]);%U_(i-1,j)
U_00=circshift(U,[0,0]);%U_(i,j)
U_p0=circshift(U,[0,-1]);%U_(i+1,j)
%U_np=circshift(U,[-1,1]);%U_(i-1,j+1)
U_0p=circshift(U,[-1,0]);%U_(i,j+1)
%U_pp=circshift(U,[-1,-1]);%U_(i+1,j+1)
L=(U_p0-2*U_00+U_n0+U_0p-2*U_00+U_0n)/1/dx^2;
end
function L = Laplace_Diff9(U,dx)
%9点Laplace差分格式
U_nn=circshift(U,[1,1]);%U_(i-1,j-1)
U_0n=circshift(U,[1,0]);%U_(i,j-1)
U_pn=circshift(U,[1,-1]);%U_(i+1,j-1)
U_n0=circshift(U,[0,1]);%U_(i-1,j)
U_00=circshift(U,[0,0]);%U_(i,j)
U_p0=circshift(U,[0,-1]);%U_(i+1,j)
U_np=circshift(U,[-1,1]);%U_(i-1,j+1)
U_0p=circshift(U,[-1,0]);%U_(i,j+1)
U_pp=circshift(U,[-1,-1]);%U_(i+1,j+1)
L=(-20*U_00+4*U_p0+4*U_n0+4*U_0p+4*U_0n+U_nn+U_pn+U_np+U_pp)/6/dx^2;
end
变化过程中的动图如下:
3 LE模型(CIMA反应)
CIMA反应是1990年,由Castets等人研究并发现的。Lengyel、Rabai 和 Epstein 等人提出了一种相应的反应扩散模型,用于CIMA反应的数值分析,被称为 Lengyel-Epstein (LE) 模型。
其方程可以写作:
α → U U → V 4 U + V → Ω S + U ↔ S U \alpha \to U \\ U \to V \\ 4U+V \to \Omega \\ S+U\leftrightarrow SU α→UU→V4U+V→ΩS+U↔SU
其微分方程可以写作:
∂ U ∂ t = Δ U + a − U − 4 U V 1 + U 2 ∂ V ∂ t = σ [ c Δ V + b ( U − U V 1 + U 2 ) ] \frac{\partial U}{\partial t} =\Delta U+a-U-4\frac{UV}{1+U^2} \\ ~\\ \frac{\partial V}{\partial t} =\sigma [c\Delta V+b(U-\frac{UV}{1+U^2})] ∂t∂U=ΔU+a−U−41+U2UV ∂t∂V=σ[cΔV+b(U−1+U2UV)]
同上文第二章,将方程离散化,时间项采用一阶欧拉法,拉普拉斯项采用相应的5点或9点差分格式。
接下来是常数、边界、初始值的选取:
常数(理解之前,尽量不要动这些常数):
时间步长dt=0.002,空间网格dx=0.5。因为这个方程比较容易发散,时间精度一阶也比较差,所以只能靠调小时间步长来解决发散问题。
σ = 20 \sigma=20 σ=20
c = 20 c=20 c=20
这里a、b的选取,参照论文:Morphology of Experimental and Simulated Turing Patterns (2009)
我给几个示例:
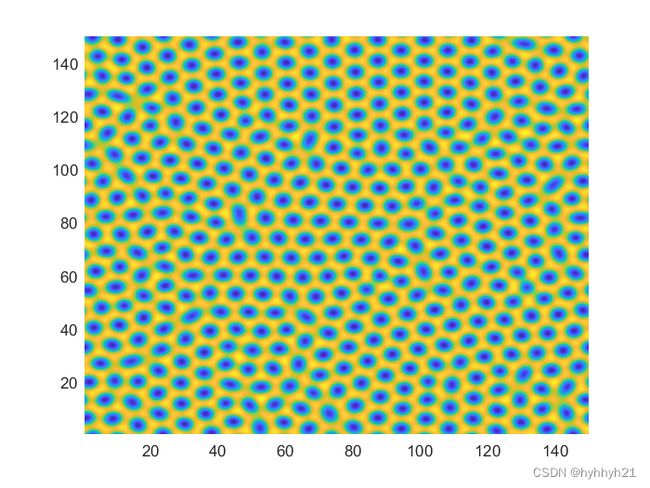
a=12.2,b=0.30 图灵斑1
a=12.8,b=0.28 图灵斑2
a=12.0,b=0.37 孔洞图案
边界条件采用循环边界条件,实现方法为,用circshift函数来获取 U i + 1 , j U_{i+1,j} Ui+1,j之类的信息,这样就自然的满足了循环条件。
初始值U=3.5,V=7.5。之后随机背景增加了0.1的噪声。
程序代码如下:
clear
clc
close all
% LE模型
%构建网格
dt=0.002;%时间步长
N=300;%网格总数量
dx=0.5;%网格大小
x=dx*(1:N);
[X,Y]=meshgrid(x,x);
U0=ones(size(X))*3.5;
V0=ones(size(X))*7.5;
%初始化,添加随机数
U0=U0+0.1*(2*rand(size(U0))-1);
V0=V0+0.1*(2*rand(size(U0))-1);
F=fspecial('gaussian',5,0.5);
U0=imfilter(U0,F,'circular');
V0=imfilter(V0,F,'circular');
%方程初常数
Si=20;
c=1;
%图灵斑
a=12.2;
b=0.3;
%孔洞
a=12;
b=0.37;
% %图灵斑2
% a=12.8;
% b=0.28;
%微分方程求解
U_Old=U0;
V_Old=V0;
for k_t=1:round(250/dt)
%1阶时间精度
F=U_Old.*V_Old./(1+U_Old.^2);
U_New=U_Old+(Laplace_Diff5(U_Old,dx) +a-U_Old-4*F)*dt;
V_New=V_Old+Si*(c*Laplace_Diff5(V_Old,dx)+b*U_Old-b*F)*dt;
U_Old=U_New;
V_Old=V_New;
%绘图
if mod(k_t,1500)==1
figure(1)
clf
pcolor(X,Y,U_New);shading interp
pause(0.01)
end
end
function L = Laplace_Diff5(U,dx)
%5点Laplace差分格式
%U_nn=circshift(U,[1,1]);%U_(i-1,j-1)
U_0n=circshift(U,[1,0]);%U_(i,j-1)
%U_pn=circshift(U,[1,-1]);%U_(i+1,j-1)
U_n0=circshift(U,[0,1]);%U_(i-1,j)
U_00=circshift(U,[0,0]);%U_(i,j)
U_p0=circshift(U,[0,-1]);%U_(i+1,j)
%U_np=circshift(U,[-1,1]);%U_(i-1,j+1)
U_0p=circshift(U,[-1,0]);%U_(i,j+1)
%U_pp=circshift(U,[-1,-1]);%U_(i+1,j+1)
L=(U_p0-2*U_00+U_n0+U_0p-2*U_00+U_0n)/1/dx^2;
end
function L = Laplace_Diff9(U,dx)
%9点Laplace差分格式
U_nn=circshift(U,[1,1]);%U_(i-1,j-1)
U_0n=circshift(U,[1,0]);%U_(i,j-1)
U_pn=circshift(U,[1,-1]);%U_(i+1,j-1)
U_n0=circshift(U,[0,1]);%U_(i-1,j)
U_00=circshift(U,[0,0]);%U_(i,j)
U_p0=circshift(U,[0,-1]);%U_(i+1,j)
U_np=circshift(U,[-1,1]);%U_(i-1,j+1)
U_0p=circshift(U,[-1,0]);%U_(i,j+1)
U_pp=circshift(U,[-1,-1]);%U_(i+1,j+1)
L=(-20*U_00+4*U_p0+4*U_n0+4*U_0p+4*U_0n+U_nn+U_pn+U_np+U_pp)/6/dx^2;
end
设置不同的a和b,输出的结果也会有所不同,会呈现出从斑图到点图的各种变化。