Leetcode365 水壶问题
leetcode 水壶问题
水壶问题
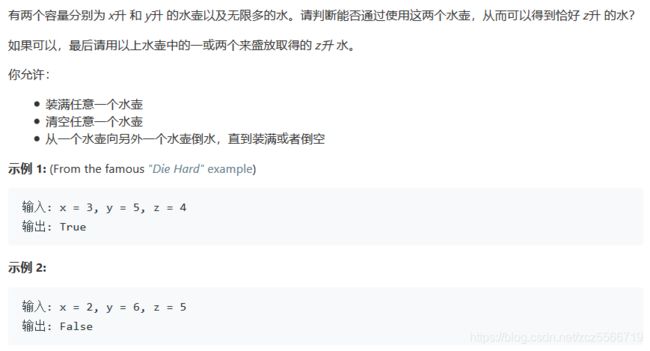 每日一题,有点偏数学,但是可以用图论的BFD 和DFS 求解。
每日一题,有点偏数学,但是可以用图论的BFD 和DFS 求解。
关于二叉树的BFS和DFS已经进行过介绍,本文主要是图论的BFS和DFS。
首先对题目进行建模。观察题目可知,在任意一个时刻,此问题的状态可以由两个数字决定:X 壶中的水量,以及 Y 壶中的水量。
在任意一个时刻,我们可以且仅可以采取以下几种操作或者是只存在如下的状态转移可能:
把 X 壶的水灌进 Y 壶,直至灌满或倒空;
把 Y 壶的水灌进 X 壶,直至灌满或倒空;
把 X 壶灌满;
把 Y 壶灌满;
把 X 壶倒空;
把 Y 壶倒空。
因此可以用搜索的方法解决问题。
首先是广度优先
class Solution(object):
def canMeasureWater(self, x, y, z):
"""
:type x: int
:type y: int
:type z: int
:rtype: bool
"""
# bfs
from collections import deque
queue = deque([[0, 0]]) # 双向队列
visited = set([(0, 0)]) # 标记哪些状态已经处理过了
# 开始递推状态
while queue:
cur_x, cur_y = queue.pop() # 广度优先
# 结束循环的条件
if z in [cur_x, cur_y, cur_x + cur_y]:
return True
# 可能转移到下列可能的状态
for item in [
# 加满水
(x, cur_y), (cur_x, y),
# 清空水
(0, cur_y), (cur_x, 0),
# x -> y
(cur_x + cur_y - y, y) if cur_x + cur_y >= y else (0, cur_x + cur_y),
# y -> x
(x, cur_x + cur_y - x) if cur_x + cur_y >= x else (cur_x + cur_y, 0)]:
# 为防止成环,对邻居进行标记
if item not in visited:
queue.appendleft(item)
visited.add(item)
return False
这种方法的在得到结果的时候就会结束,不用遍历整个图,相对复杂度比较低。
深度优先
class Solution:
def canMeasureWater(self, x: int, y: int, z: int) -> bool:
visited = set()
def helper(cur_x, cur_y):
# print(cur_x, cur_y)
if z in [cur_x, cur_y, cur_x + cur_y]:
return True
for item in [
# 加满水
(x, cur_y), (cur_x, y),
# 清空水
(0, cur_y), (cur_x, 0),
# x -> y
(cur_x + cur_y - y, y) if cur_x + cur_y >= y else (0, cur_x + cur_y),
# y -> x
(x, cur_x + cur_y - x) if cur_x + cur_y >= x else (cur_x + cur_y, 0)]:
if item not in visited:
visited.add(item)
if helper(*item): return True
visited.remove(item)
return False
return helper(x, y)
数学方法
裴蜀定理
若a,b是整数,且gcd(a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立
class Solution:
def canMeasureWater(self, x: int, y: int, z: int) -> bool:
import math
if x + y < z: return False
if x == z or y == z or x + y == z: return True
return z % math.gcd(x, y) == 0