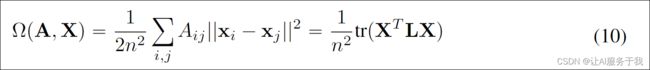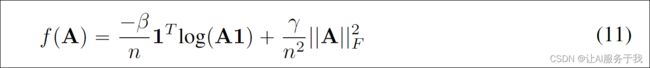Iterative Deep Graph Learning for Graph Neural Networks: Better and Robust Node Embeddings
摘要:在本文中,我们提出了一个端到端的图学习框架,即迭代深度图学习(IDGL),用于联合和迭代地学习图结构和图嵌入。IDGL的关键理论是基于更好的节点嵌入来学习更好的图结构,反之亦然(即基于更好的图结构来学习更好的节点嵌入)。我们的迭代方法在学习到的图结构足够接近于下游预测任务优化的图时动态停止。此外,我们将图学习问题作为相似度度量学习问题,并利用自适应图正则化来控制学习图的质量。最后,我们结合锚点近似技术,进一步提出了IDGL的可扩展版本,即IDGL-ANCH,它显著降低了IDGL的时间和空间复杂度,同时不影响性能。我们在九个基准测试中进行了广泛实验,结果表明我们提出的IDGL模型可以始终优于或与最先进的基线模型相匹配。此外,IDGL在处理对抗性图和处理传导性和归纳性学习方面更具有鲁棒性。
1 介绍
近年来,图神经网络(GNN)受到了越来越多的关注,尤其是在开发更有效的GNN用于节点分类[29,36,17,52]、图分类[60,43]和图生成[47,37,61]方面做出了不懈的努力。尽管GNN具有学习表达性节点嵌入的强大能力,但不幸的是,它们只能在有图结构的数据可用时使用。许多实际应用自然地采用网络结构数据(例如社交网络)。然而,这些内在的图结构并不总是下游任务的最佳选择。部分原因是原始图是从原始特征空间构建的,可能不反映特征提取和转换后的“真实”图拓扑。另一个潜在的原因是,由于数据测量或收集时难免存在误差,真实世界的图往往存在噪声或甚至不完整。此外,许多应用程序(如自然语言处理[7,57,58])可能仅具有序列数据或甚至只有原始特征矩阵,需要从原始数据矩阵中构建额外的图。
为了解决这些限制,我们提出了一个端到端的图学习框架,即迭代深度图学习(IDGL),用于联合迭代学习图结构和GNN参数,这些参数针对下游预测进行了优化。
IDGL框架的关键是在更好的节点嵌入的基础上学习更好的图结构,同时,在更好的图构造的基础上,学习更好的节点嵌入。特别是,IDGL是一种新的迭代方法,旨在搜索一种隐式图结构,该隐式图构造扩充了初始图结构(如果不可用,我们使用kNN图),目的是优化下游预测任务的图。当学习到的图结构足够接近为下游任务优化的图时,迭代方法调整何时在每个小批量中停止。
此外,我们提出了一种使用多头自注意力和ε-邻域稀疏化构建图的图学习神经网络。此外,与[25]中直接优化邻接矩阵而不考虑下游任务的方法不同,我们通过优化联合损失来学习图度量学习函数,该联合损失结合了任务特定的预测损失和图正则化损失。最后,我们进一步提出了我们IDGL框架的可扩展版本,即IDGL-ANCH,通过结合基于锚点的逼近技术,将时间和内存复杂度从与图节点数量平方成正比降至与图节点数量线性成正比。
简而言之,我们将主要贡献总结如下:
- 我们提出了一种新的端到端图学习框架(IDGL),用于联合迭代学习图结构和图嵌入。当学习的图结构接近优化的图(用于预测)时,IDGL动态停止。据我们所知,我们是第一个将迭代学习引入图结构学习的。
- 结合基于锚点的近似技术,我们进一步提出了IDGL的可扩展版本,即IDGL-ANCH,它在计算时间和内存消耗方面都实现了相对于图节点数量的线性复杂性。
- 实验结果表明,我们的模型在各种下游任务上始终优于或匹配最先进的基线。更重要的是,IDGL可以对对抗性图示例更具鲁棒性,并且可以处理转导学习和归纳学习。
2 迭代的深度图学习框架
2.1 问题公式化
假设图G为 G = ( V , E ) G = (V, E) G=(V,E),由n个节点 v i ∈ V v_i \in V vi∈V组成,具有一个初始节点特征矩阵 X ∈ R d × n X \in \mathbb{R}^{d \times n} X∈Rd×n,边 ( v i , v j ) ∈ E ({v_i, v_j}) \in E (vi,vj)∈E(二元或加权)形成一个初始的带噪声邻接矩阵 A ( 0 ) ∈ R n × n A^{(0)} \in \mathbb{R}^{n \times n} A(0)∈Rn×n,和一个度矩阵 D i i ( 0 ) = ∑ j A i j ( 0 ) D^{(0)}_{ii} = \sum_{j} A^{(0)}_{ij} Dii(0)=∑jAij(0)。给定一个带噪声的图输入 G : ( A ( 0 ) , X ) G:({A^{(0)},X}) G:(A(0),X)或仅有一个特征矩阵 X ∈ R d × n X \in \mathbb{R}^{d \times n} X∈Rd×n,我们在本文中考虑的深度图学习问题是,产生一个优化的图 G ∘ : ( A ∘ , X ) G^{\circ}:({A^{\circ},X}) G∘:(A∘,X)及其相应的图节点嵌入 Z = f G ∘ , θ ( G ∘ ) ∈ R h × n Z=f_{G^{\circ},\theta}(G^{\circ}) \in \mathbb{R}^{h \times n} Z=fG∘,θ(G∘)∈Rh×n,关于某个(半)监督下游任务。值得注意的是,我们假设图噪声只来自图的拓扑结构(邻接矩阵),而节点特征矩阵 X X X是无噪声的。当图的拓扑结构和节点特征矩阵都存在噪声时,这种情况更具挑战性,将作为我们未来工作的一部分。在不失一般性的情况下,本文中考虑了节点级和图级预测任务。
图拓扑对于GNN学习表达型图节点嵌入至关重要。大多数现有的GNN方法只是假设输入图拓扑是完美的。这在实践中不一定是真的,因为真实世界的图通常是有噪声的或不完整的。更重要的是,所提供的输入图可能不适合监督的下游任务,因为大多数原始图是从原始特征空间构建的,在高级特征转换后,原始特征空间可能无法反映“真实”的图拓扑。一些先前的工作[52]通过对先前学习的节点嵌入使用自注意来重新加权邻域节点嵌入的重要性来缓解这一问题,该自注意仍然假设原始图连通性信息是无噪声的。
为了处理潜在的噪声输入图,我们提出了我们新的IDGL框架,该框架将问题公式化为迭代学习问题,该问题联合学习图结构和GNN参数。我们的IDGL框架的关键原理是基于更好的节点嵌入来学习更好的图结构,同时,基于更好的图构造来学习更好地节点嵌入,如图所示。2。与大多数现有的基于原始节点特征构建图的方法不同,GNN学习的节点嵌入(针对下游任务进行优化)可以为学习更好的图结构提供有用的信息。另一方面,新学习的图结构可以是GNN学习更好的节点嵌入的更好的图输入。
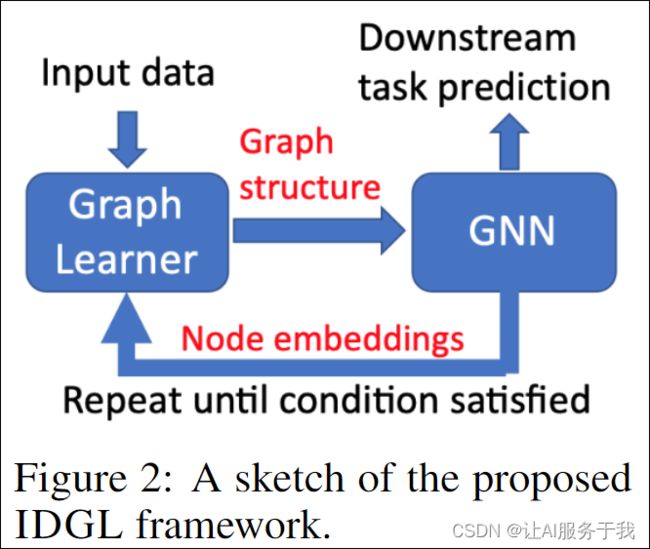
特别是,IDGL是一种新的迭代方法,旨在搜索一种隐式图结构,该隐式图结构化为下游预测任务扩充初始图结构(如果不可用,我们使用kNN图)。基于我们提出的停止准则,当学习到的图结构足够接近优化图(相对于下游任务)时,迭代方法在每个小批量中动态停止。此外,可以以端到端的方式针对下游任务优化图构建过程.
2.3 图的相似性度量学习
之前的方法(例如[15])将图学习问题建模为在图的边缘上学习联合离散概率分布,已经表现出了很好的性能。但是,由于它们假设图节点已知,通过优化边缘连接性无法处理归纳设置(即在测试期间有新节点的情况)。为了解决这个问题,我们将图结构学习问题视为相似度度量学习,该度量将与专门用于下游任务的预测模型一起进行联合训练。
图相似性度量学习 度量学习的常见选项包括余弦相似性[44,54]、径向基函数(RBF)核[59,34]和注意力机制[51,23]。一个好的相似性度量函数应该是可学习的并且具有强大的表达能力。尽管我们的框架对各种相似性度量函数是不可知的,但在不失一般性的情况下,我们设计了加权余弦相似性作为我们的度量函数,将 s i j s_{ij} sij定义为以下相似度度量函数: s i j p = cos ( w p ⊙ v i , w p ⊙ v j ) ( 1 ) s^p_{ij} = \cos(\mathbf{w_p} \odot \mathbf{v_i}, \mathbf{w_p} \odot \mathbf{v_j}) \\(1) sijp=cos(wp⊙vi,wp⊙vj)(1),其中d表示Hadamard积,w是一个可学习的权重向量,与输入向量vi和vj具有相同的维度,并学习突出向量的不同维度。注意,两个输入向量可以是原始节点特征或计算节点嵌入。
为了稳定学习过程并增强表现力,我们将相似度度量函数扩展到多头版本(类似于[51, 52]中的观察结果)。具体而言,我们使用m个权重向量(每个向量代表一种视角)来使用上述相似度函数计算m个独立的相似度矩阵,并将它们的平均值作为最终相似度: s i j = 1 m ∑ p = 1 m s i j p s_{ij} = \frac{1}{m} \sum_{p=1}^{m} s^p_{ij} sij=m1p=1∑msijp其中, s i j s_{ij} sij表示在第p个视角下计算 v i v_i vi和 v j v_j vj之间的余弦相似度,其中每个视角考虑向量中的不同语义部分。
使用 ε ε ε-邻域进行图稀疏化 通常,从度量计算得出的邻接矩阵应该是非负的,但是 s i j s_{ij} sij的范围在 [ − 1 , 1 ] [-1,1] [−1,1]之间。此外,许多基础图结构比完全连接的图更稀疏,这不仅计算成本高昂,而且可能会引入噪声(即不重要的边)。因此,我们通过仅考虑每个节点的ε-邻域,从 S S S中提取一个对称的稀疏非负邻接矩阵 A A A。具体而言,我们将 S S S中小于非负阈值 ε ε ε的元素掩码(即设为零)。
基于锚点的可扩展度量学习 类似于公式(1)的上述相似度度量函数计算所有图节点对的相似度得分,这需要 O ( n 2 ) O(n^2) O(n2)的计算时间和内存消耗,从而在大型图中出现了显著的可扩展性问题。为了解决可扩展性问题,受以前基于锚点的方法[41, 55]的启发,我们设计了一种基于锚点的可扩展度量学习技术,该技术学习了一个节点-锚点亲和矩阵 R ∈ R n × s R \in \mathbb{R}^{n \times s} R∈Rn×s(即时间和空间复杂度都需要 O ( n s ) O(ns) O(ns),其中 s s s是锚点的数量)来描述节点集合 V V V和锚点集合 U U U之间的关系。请注意, s s s是一个超参数,可以在开发集上进行调整。
具体而言,在大型图中,我们从节点集合 V V V 中随机抽取一组大小为 s ∈ U s \in U s∈U 的锚点集合,其中 s s s 通常远小于 n n n。因此,锚点嵌入被设置为相应的节点嵌入。因此,公式(1)可以重写为以下形式: a i k p = cos ( w p ⊙ v i , w p ⊙ u k ) , a i k p = 1 m ∑ p = 1 m a i k p ( 2 ) a^p_{ik} = \cos(\mathbf{w_p} \odot \mathbf{v_i}, \mathbf{w_p} \odot \mathbf{u_k}), \quad a^p_{ik} = \frac{1}{m} \sum_{p=1}^{m} a^p_{ik} \\(2) aikp=cos(wp⊙vi,wp⊙uk),aikp=m1p=1∑maikp(2)
其中 a i k a_{ik} aik 是节点 v i v_i vi 和锚点 u k u_k uk 之间的亲和分数。类似地,我们将 ϵ \epsilon ϵ-邻域稀疏化技术应用于节点-锚点亲和分数 a i k a_{ik} aik,以获得稀疏且非负的节点-锚点亲和矩阵 R R R。
2.4 图节点嵌入和预测
尽管初始图可能存在噪声,但通常仍携带有关真实图拓扑的丰富和有用信息。理想情况下,学习得到的图结构 A A A可以补充原始图拓扑 A ( 0 ) A^{(0)} A(0),以针对下游任务构建优化的GNN图。因此,我们在温和的假设下认为,优化的图结构可能是从初始图结构“偏移”得来的,我们将学习得到的图与初始图结构组合起来。
A ( t ) = λ L ( 0 ) + ( 1 − λ ) [ η f ( A ( t ) ) + ( 1 − η ) f ( A ( 1 ) ) ] ( 3 ) A^{(t)} = \lambda L^{(0)} + (1 - \lambda) \left[\eta f(A^{(t)}) + (1-\eta) f(A^{(1)})\right]\\(3) A(t)=λL(0)+(1−λ)[ηf(A(t))+(1−η)f(A(1))](3)其中, L ( 0 ) = D ( 0 ) − 1 2 A ( 0 ) D ( 0 ) − 1 2 L^{(0)} = D^{(0)-\frac{1}{2}} A^{(0)}D^{(0)-\frac{1}{2}} L(0)=D(0)−21A(0)D(0)−21 是初始图的归一化邻接矩阵。 A ( t ) A^{(t)} A(t) 和 A ( 1 ) A^{(1)} A(1) 分别是第 t t t 次迭代和第 1 1 1 次迭代(使用公式(1))计算的两个邻接矩阵。邻接矩阵进一步进行行归一化,即 f ( A ) i , j = A i , j ∑ j A i , j f(A)_{i,j} = \frac{A_{i,j}}{\sqrt{\sum_j A_{i,j}}} f(A)i,j=∑jAi,jAi,j。
需要注意的是, A ( 1 ) A^{(1)} A(1) 是从原始节点特征 X X X计算得出的,而 A ( t ) A^{(t)} A(t)是从先前更新的节点嵌入 Z t − 1 Z_{t-1} Zt−1中计算得出的,该嵌入已经针对下游预测任务进行了优化。因此,我们将最终学习到的图结构作为它们的线性组合,由一个超参数 η \eta η加权,以便结合两者的优点。最后,另一个超参数 λ \lambda λ用于平衡学习到的图结构和初始图结构之间的权衡。如果没有这样的初始图结构,则可以使用基于余弦相似度使用原始节点特征 X X X构建的 k k k最近邻图。
我们的图学习框架对于各种GNN架构(接受节点特征矩阵和邻接矩阵作为输入来计算节点嵌入)和预测任务是不可知的。在本文中,我们采用了一个两层的GCN[29],其中第一层(表示为GNN1)将原始节点特征 X X X映射到中间嵌入空间,第二层(表示为GNN2)进一步将中间节点嵌入 Z Z Z映射到输出空间。
式(4)中, Z = ReLU ( P ( X , A , W 1 ) ) , Y = σ ( P ( Z , A , W 2 ) ) , L pred = L ( Y , y ) ( 4 ) Z = \operatorname{ReLU}(P(\mathbf{X}, \mathbf{A}, \mathbf{W}_1)),Y = \sigma(P(\mathbf{Z}, \mathbf{A}, \mathbf{W}2)),L_{\text{pred}} = \mathcal{L}(Y, y) \\(4) Z=ReLU(P(X,A,W1)),Y=σ(P(Z,A,W2)),Lpred=L(Y,y)(4),其中 σ \sigma σ和 L \mathcal{L} L分别为任务相关的输出函数和损失函数。例如,对于分类任务, σ \sigma σ是一个softmax函数,用于预测一组类别的概率分布, L \mathcal{L} L是一个交叉熵函数,用于计算预测损失。 P ( ⋅ ) P(\cdot) P(⋅)是一个消息传递函数,在GCN中, P ( F , A ) = A F W P(F, \mathbf{A}) = \mathbf{A} F \mathbf{W} P(F,A)=AFW,其中 F F F是一个特征/嵌入矩阵, A \mathbf{A} A是通过使用公式(3)获得的归一化邻接矩阵。
Node-anchor消息传递:
需要注意的是,一个节点-锚点亲和力矩阵 R R R可以作为二分图 B B B的加权邻接矩阵,只允许节点和锚点之间的直接连接。如果我们将节点和锚点之间的直接转移视为由 R R R描述的一步转移,建立在平稳马尔可夫随机游走理论[42]的基础上,我们实际上可以通过计算两步转移概率来从 R R R中恢复节点图 G G G和锚点图 Q Q Q。设 A ∈ R n × n A \in \mathbb{R}^{n \times n} A∈Rn×n是节点图 G G G的行标准化邻接矩阵, A i j = p ( 2 ) ( v j ∣ v i ) A_{ij} = p^{(2)}(v_j|v_i) Aij=p(2)(vj∣vi)表示从节点 v i v_i vi到 v j v_j vj的两步转移概率,则可以从 R R R中恢复 A A A。
A = Δ − 1 R Λ − 1 R T ( 5 ) A = \Delta^{-1} R \Lambda^{-1} R^T\\(5) A=Δ−1RΛ−1RT(5)
其中 Λ ∈ Rs×s (Λkk = Σi=1n Rik) 和 Δ ∈ Rn×n (Δii = Σk=1s Rik) 都是对角矩阵。类似地,我们可以恢复锚图 Q 的行归一化邻接矩阵 B ∈ Rs×s:
B = Λ − 1 R T Δ − 1 R ( 6 ) B = Λ^{-1}R^TΔ^{-1}R\\ (6) B=Λ−1RTΔ−1R(6)
有兴趣的自己看看吧,矫正公式太浪费时间,其实讲的是以前消息传递是基于A去传递的,现在变成了节点到锚点,然后锚点再到节点这样一个过程,然后把上面提到的基于A计算的公式替换成了基于节点-锚点-节点的计算公式
2.5 图的正则化
虽然将学习到的图Aptq与初始图Ap0q结合是接近优化图的有效方法,但学习到的图Aptq的质量对于提高最终图rAptq的质量起着重要作用。在实践中,控制生成的学习图Aptq的平滑性、连通性和稀疏性非常重要,这能够忠实地反映出与初始节点属性X和下游任务相关的图拓扑结构。
假设将特征矩阵X的每一列视为图信号。对于图信号,广泛采用的假设是相邻节点之间的值变化平滑。给定一个带权重对称邻接矩阵A的无向图,通常通过Dirichlet能量进行度量,如下所示:
其中,tr(·)表示矩阵的迹,L=D-A是图拉普拉斯矩阵,D是度矩阵,定义为 D = d i a g ( ∑ j A i j ) D=diag(∑_jA_{ij}) D=diag(∑jAij)。通过最小化Dirichlet能量,可以强制要求相邻节点具有相似的特征,从而实现在与A相关联的图上的图信号平滑。
然而,仅最小化平滑损失将导致平凡解A=0。此外,希望能够控制生成的图的稀疏性。按照[25]的方法,我们对学习到的图施加额外的约束,如下所示:
其中, ∣ ∣ A ∣ ∣ F ||A||_F ∣∣A∣∣F表示Frobenius范数, f ( A ) f(A) f(A)是对图A的惩罚函数。这些约束将鼓励学习到的图具有更强的稀疏性。这些内容可以在我上一篇关于图结构学习的内容中找到。我们将总体图正则化损失定义为上述损失的总和,即 L G = α Ω ( A , X ) + f ( A ) L_G = αΩ(A,X) + f(A) LG=αΩ(A,X)+f(A),其中 α α α、 β β β和 γ γ γ均为非负超参数,这有助于控制学习图的平滑性、连通性和稀疏性。
锚点图正则化 如公式(6)所示,我们可以在 O ( n s 2 ) O(ns^2) O(ns2)时间复杂度内获得锚点图 Q Q Q的行归一化邻接矩阵 B B B。为了控制学习到的节点-锚点亲和矩阵 R R R的质量(这可以隐式地控制节点邻接矩阵 A A A的质量),我们将上述图正则化技术应用于锚点图。值得注意的是,我们提出的图正则化损失仅适用于非负对称邻接矩阵[26]。因此,我们选择将图正则化应用于其未归一化版本 B B B,而不是常常不对称的 B B B,其中 L G = α Ω ( B ^ , X U ) + f ( B ^ ) L_G = αΩ(\hat B,X^U)+ f(\hat B) LG=αΩ(B^,XU)+f(B^),其中 X U X^U XU表示从节点嵌入 X X X中抽样的锚点嵌入集合。
2.6 混合损失的联合学习
与直接基于图正则化损失[26]或任务相关预测损失[15]优化邻接矩阵的以往工作相比,我们提出了一种联合迭代学习图结构和GNN参数的方法,通过最小化混合损失函数 L = L p r e d + L G L = L_{pred} + L_G L=Lpred+LG 来实现,其中 L p r e d L_{pred} Lpred和 L G L_G LG分别为任务预测损失和图正则化损失。IDGL框架的完整算法在算法1中给出。可以看到,我们的模型使用更新的节点嵌入(公式(1))反复优化邻接矩阵,并使用更新的邻接矩阵(公式(3)和(4))优化节点嵌入,直到连续迭代之间邻接矩阵之间的差异小于某个阈值。需要注意的是,相比于全局使用固定的迭代次数,我们的动态停止准则更加有利,特别是对于小批量训练。在每次迭代中,计算既考虑任务相关预测损失又考虑图正则化损失的混合损失。在所有迭代之后,将整体损失通过所有先前的迭代进行反向传播,以更新模型参数。值得注意的是,算法1同样适用于IDGL-ANCH。IDGL和IDGL-ANCH之间的主要区别在于我们如何计算邻接(或亲和)矩阵,以及如何执行消息传递和图正则化。
3 实验
在本节中,我们进行了广泛的实验,以验证IDGL和IDGL-ANCH在各种设置中的有效性。我们提出的模型的实施可在Code.
数据集和基线 我们实验中使用的基准数据集包括四个引文网络数据集(即Cora、Citeseer、Pubmed和ogbn-arxiv)[48,21],其中图拓扑结构是可用的,三个非图数据集(即Wine、Breast Cancer(Cancer)和Digits)[11],其中没有图拓扑结构,以及两个文本基准(即20Newsgroups数据(20News)和电影评论数据(MRD))[32,46],我们将文档视为一个包含每个单词的节点的图。前七个数据集都是在传递性设置下的节点分类任务,我们遵循以前的工作的实验设置[29,15,21]。后两个数据集是在归纳性设置下的图级预测任务。有关详细的数据统计,请参见附录C.1。我们的主要基准线是LDS [15],但它不能处理归纳学习问题,因此我们只报告其在传递性数据集上的结果。此外,对于引文网络数据集,我们包括其他GNN变体(即GCN [29]、GAT [52]、GraphSAGE [18]、APPNP [30]、H-GCN [20]和GDC [31])作为基准。对于没有图拓扑结构的非图和文本基准,我们构建了各种 G N N k N N GNN_{kNN} GNNkNN基线(即 G C N k N N GCN_{kNN} GCNkNN、 G A T k N N GAT_{kNN} GATkNN和 G r a p h S A G E k N N GraphSAGE_{kNN} GraphSAGEkNN),其中在应用GNN模型之前,在数据集上构建了一个kNN图。对于文本基准,我们包括一个BiLSTM [19]基准。报告的结果是在具有不同随机种子的5个运行中平均的。
实验结果 表1显示了传递性实验的结果。首先,IDGL在5个基准测试中的4个中表现优于所有基线。此外,相比于IDGL,IDGL-ANCH更具可扩展性,可以达到相当甚至更好的结果。在图结构可用的情况下,与最先进的GNN和图学习模型相比,我们的模型即使基于基本的GCN,也可以实现显著更好或具有竞争力的结果。当图拓扑结构不可用时(因此GNN不能直接应用),与图学习基准相比,IDGL在所有数据集上都能够始终实现更好的结果。与我们的主要图学习基线LDS相比,我们的模型不仅性能显著更好,而且更具可扩展性。归纳实验的结果如表2所示。与LDS无法处理归纳设置不同,20News和MRD上的良好表现证明了IDGL在归纳学习上的能力。

消融实验 表3显示了我们模型中不同模块的消融研究结果。通过关闭迭代学习组件(即仅迭代一次),我们可以看到IDGL和IDGL-ANCH在所有数据集上的性能持续显著下降,表明其有效性。此外,我们可以看到在图正则化损失的情况下联合训练模型的好处。


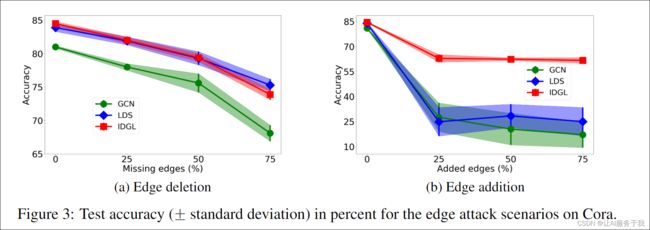
模型分析 为了评估IDGL对对抗性图的鲁棒性,我们构造了具有随机边缘删除或添加的图。具体来说,对于原始图中的每对节点,我们随机移除(如果存在边)或添加(如果没有这样的边)一条边,概率为25%、50%或75%。如图3所示,与GCN和LDS相比,IDGL在两种情况下都取得了更好或可比的结果。虽然GCN和LDS在边缘添加场景中都完全失败,但IDGL的表现相当不错。我们推测这是因为通过在初始图中加入误导性的加性随机噪声,边缘添加场景比边缘删除场景更具挑战性。并且方程。(3)被公式化为跳跃连接的形式,通过降低λ的值(即,在发展集上调整),我们强制模型减少对初始噪声图的依赖。

在图4a(以及附录B.1)中,我们展示了在测试阶段迭代学习过程中学到的邻接矩阵和准确率的演变。我们计算相邻迭代之间邻接矩阵的差异为 δ A ( t ) = ∣ ∣ A ( t ) − A ( t − 1 ) ∣ ∣ F 2 / ∣ ∣ A ( t ) ∣ ∣ F 2 \delta^{(t)}_A=||A^{(t)}-A^{(t-1)}||^2_F / ||A^{(t)}||^2_F δA(t)=∣∣A(t)−A(t−1)∣∣F2/∣∣A(t)∣∣F2,通常在0到1之间。我们可以看到,邻接矩阵和准确率都很快地收敛。这从经验上验证了我们在附录A.2中对IDGL收敛性质的分析。请注意,这种收敛性质并不是由于GNN的过度平滑效应[56,33],因为我们在实验中只使用了两层GCN作为IDGL的底层GNN模块。
我们比较了IDGL和IDGL-ANCH与其他基线的训练效率。如表4所示,IDGL始终比LDS快,但总体上它们是可比的。请注意,IDGL的可训练参数数量与LDS相当。例如,在Cora数据上,IDGL的可训练参数数量为28,836,而LDS为23,040。而我们看到IDGL-ANCH相比于IDGL有大幅度的加速。请注意,由于内存限制,我们无法在Pubmed上运行IDGL。理论复杂度分析提供在附录A.3中。
我们还对停止策略进行了实证研究(图4b和附录B.2),展示了IDGL学习的图形结构(附录B.3),并进行了超参数分析(附录B.4)。模型设置的详细信息在附录C.2中提供。

4 相关工作
从不同的角度,在不同领域中广泛研究了图结构学习的问题。在图形信号处理的领域中,研究人员探索了从数据[10、12、53、27、3、1]中学习图形的各种方法,并在图表上具有某些结构约束(例如,稀疏性)。在聚类分析的文献[4,22]中也研究了这个问题,他们的目的是同时构成聚类任务并学习对象之间的相似性关系。这些作品都集中在无监督的学习设置上,而无需考虑任何有监督的下游任务,并且无法处理归纳学习问题。其他相关的作品包括概率图形模型[9,66,62]和图生成[38,49]中的结构推断,其目标与我们的目标不同。在GNN的领域[29、16、18、35、63]中,有一系列关于开发强大的GNN [50]的研究,通过利用基于注意的方法[5],贝叶斯方法,贝叶斯方法[13)[13,64],基于图扩散的方法[31]以及图形上的各种假设(例如,低等级和稀疏性)[14,24,65]。这些方法通常假定初始图形结构可用。最近,研究人员探索了自动构建对象图[45、8、34、15、40]或单词[39、6、7]的方法。但是,这些方法只是在不明确控制学到的图形质量的情况下优化了朝向下游任务的图形。最近,[15]提出了通过利用双光线优化技术联合学习图形和GNN的参数的LDS模型。但是,根据设计,他们的方法无法处理归纳设置。我们的工作还与类似变压器的方法[51]有关,该方法通过利用多头注意机制来学习对象之间的关系。但是,这些方法不集中在图形学习问题上,也没有设计用于使用初始图形结构。
5 结论
我们提出了一种新的IDGL框架,用于联合迭代学习为下游任务优化的图结构和嵌入。实验结果证明了所提出的模型的有效性和效率。在未来,我们计划探索有效的技术来处理图拓扑和节点特征都有噪声的更具挑战性的场景。
更广泛的影响
我们研究的基本目标是开发一种联合学习图结构和嵌入的方法,该方法针对(半)监督的下游任务进行优化。我们的技术可以广泛应用于各种应用,包括社交网络分析、自然语言处理(如问答和文本生成)、药物发现和社区检测。从概念上讲,任何旨在联合学习图结构和嵌入以便在下游任务中表现良好的应用程序。这些潜在的应用包括计算机视觉、自然语言处理和网络分析。例如,我们的研究可以用来帮助更好地捕捉自然语言处理中单词标记之间的语义关系(标记序列之外)。使用我们的方法作为工具有很多好处,例如将图神经网络应用于非图结构化数据,而无需手动构建图,以及学习对噪声输入图更具鲁棒性的节点/图嵌入。这些可能被大量潜在应用所利用的好处可能会产生广泛的社会影响:
- 使用我们的研究可以改善和加快从有噪声/不完整的图(如社交网络)甚至非图结构数据(如文本和图像)中学习有意义的图的过程。
- 使用我们的研究可以提高图神经网络对噪声/不完整图结构数据的鲁棒性,为下游任务学习良好的节点/图嵌入。
我们鼓励研究人员在更具体的现实世界应用中探索类似的方法。我们还建议进行研究,以了解在安全/安保关键应用中使用图神经网络的对抗性鲁棒性。
References
[1] X. Bai, L. Zhu, C. Liang, J. Li, X. Nie, and X. Chang. Multi-view feature selection via
nonnegative structured graph learning. Neurocomputing, 2020.
[2] M. Belkin and P. Niyogi. Laplacian eigenmaps and spectral techniques for embedding and
clustering. In Advances in neural information processing systems, pages 585–591, 2002.
[3] P. Berger, G. Hannak, and G. Matz. Efficient graph learning from noisy and incomplete data.
IEEE Transactions on Signal and Information Processing over Networks, 6:105–119, 2020.
[4] A. Bojchevski, Y. Matkovic, and S. Günnemann. Robust spectral clustering for noisy data:
Modeling sparse corruptions improves latent embeddings. In Proceedings of the 23rd ACM
SIGKDD International Conference on Knowledge Discovery and Data Mining, pages 737–746,
2017.
[5] H. Chen, L. Wang, S. Wang, D. Luo, W. Huang, and Z. Li. Label aware graph convolutional
network–not all edges deserve your attention. arXiv preprint arXiv:1907.04707, 2019.
[6] Y. Chen, L. Wu, and M. J. Zaki. Graphflow: Exploiting conversation flow with graph neural
networks for conversational machine comprehension. arXiv preprint arXiv:1908.00059, 2019.
[7] Y. Chen, L. Wu, and M. J. Zaki. Reinforcement learning based graph-to-sequence model for
natural question generation. arXiv preprint arXiv:1908.04942, 2019.
[8] E. Choi, Z. Xu, Y. Li, M. W. Dusenberry, G. Flores, Y. Xue, and A. M. Dai. Graph convolutional
transformer: Learning the graphical structure of electronic health records. arXiv preprint
arXiv:1906.04716, 2019.
[9] J. Cussens. Bayesian network learning with cutting planes. arXiv preprint arXiv:1202.3713,
2012.
[10] X. Dong, D. Thanou, P. Frossard, and P. Vandergheynst. Learning laplacian matrix in smooth
graph signal representations. IEEE Transactions on Signal Processing, 64(23):6160–6173,
2016.
[11] D. Dua and C. Graff. UCI machine learning repository, 2017.
[12] H. E. Egilmez, E. Pavez, and A. Ortega. Graph learning from data under laplacian and structural
constraints. IEEE Journal of Selected Topics in Signal Processing, 11(6):825–841, 2017.
[13] P. Elinas, E. V. Bonilla, and L. Tiao. Variational inference for graph convolutional networks in
the absence of graph data and adversarial settings. arXiv, pages arXiv–1906, 2019.
[14] N. Entezari, S. A. Al-Sayouri, A. Darvishzadeh, and E. E. Papalexakis. All you need is low
(rank) defending against adversarial attacks on graphs. In Proceedings of the 13th International
Conference on Web Search and Data Mining, pages 169–177, 2020.
[15] L. Franceschi, M. Niepert, M. Pontil, and X. He. Learning discrete structures for graph neural
networks. arXiv preprint arXiv:1903.11960, 2019.
[16] J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals, and G. E. Dahl. Neural message passing
for quantum chemistry. In Proceedings of the 34th International Conference on Machine
Learning-Volume 70, pages 1263–1272. JMLR. org, 2017.
[17] W. Hamilton, Z. Ying, and J. Leskovec. Inductive representation learning on large graphs. In
Advances in Neural Information Processing Systems, 2017.
[18] W. Hamilton, Z. Ying, and J. Leskovec. Inductive representation learning on large graphs. In
Advances in Neural Information Processing Systems, pages 1024–1034, 2017.
[19] S. Hochreiter and J. Schmidhuber. Long short-term memory. Neural computation, 9(8):1735–
1780, 1997.
[20] F. Hu, Y. Zhu, S. Wu, L. Wang, and T. Tan. Semi-supervised node classification via hierarchical
graph convolutional networks. arXiv preprint arXiv:1902.06667, 2019.
[21] W. Hu, M. Fey, M. Zitnik, Y. Dong, H. Ren, B. Liu, M. Catasta, and J. Leskovec. Open graph
benchmark: Datasets for machine learning on graphs. arXiv preprint arXiv:2005.00687, 2020.
[22] S. Huang, Z. Kang, I. W. Tsang, and Z. Xu. Auto-weighted multi-view clustering via kernelized
graph learning. Pattern Recognition, 88:174–184, 2019.
[23] B. Jiang, Z. Zhang, D. Lin, J. Tang, and B. Luo. Semi-supervised learning with graph learning-
convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and
Pattern Recognition, pages 11313–11320, 2019.
[24] W. Jin, Y. Ma, X. Liu, X. Tang, S. Wang, and J. Tang. Graph structure learning for robust graph
neural networks. arXiv preprint arXiv:2005.10203, 2020.
[25] V. Kalofolias. How to learn a graph from smooth signals. In Artificial Intelligence and Statistics,
pages 920–929, 2016.
[26] V. Kalofolias and N. Perraudin. Large scale graph learning from smooth signals. arXiv preprint
arXiv:1710.05654, 2017.
[27] Z. Kang, H. Pan, S. C. Hoi, and Z. Xu. Robust graph learning from noisy data. IEEE transactions
on cybernetics, 2019.
[28] D. P. Kingma and J. Ba. Adam: A method for stochastic optimization. arXiv preprint
arXiv:1412.6980, 2014.
[29] T. N. Kipf and M. Welling. Semi-supervised classification with graph convolutional networks.
arXiv preprint arXiv:1609.02907, 2016.
[30] J. Klicpera, A. Bojchevski, and S. Günnemann. Predict then propagate: Graph neural networks
meet personalized pagerank. arXiv preprint arXiv:1810.05997, 2018.
[31] J. Klicpera, S. Weißenberger, and S. Günnemann. Diffusion improves graph learning. In
Advances in Neural Information Processing Systems, pages 13333–13345, 2019.
[32] K. Lang. Newsweeder: Learning to filter netnews. In Machine Learning Proceedings 1995,
pages 331–339. Elsevier, 1995.
[33] Q. Li, Z. Han, and X.-M. Wu. Deeper insights into graph convolutional networks for semi-
supervised learning. In Thirty-Second AAAI Conference on Artificial Intelligence, 2018.
[34] R. Li, S. Wang, F. Zhu, and J. Huang. Adaptive graph convolutional neural networks. In
Thirty-Second AAAI Conference on Artificial Intelligence, 2018.
[35] Y. Li, D. Tarlow, M. Brockschmidt, and R. Zemel. Gated graph sequence neural networks.
arXiv preprint arXiv:1511.05493, 2015.
[36] Y. Li, D. Tarlow, M. Brockschmidt, and R. Zemel. Gated graph sequence neural networks.
International Conference on Learning Representations, 2016.
[37] Y. Li, O. Vinyals, C. Dyer, R. Pascanu, and P. Battaglia. Learning deep generative models of
graphs. arXiv preprint arXiv:1803.03324, 2018.
[38] R. Liao, Y. Li, Y. Song, S. Wang, W. Hamilton, D. K. Duvenaud, R. Urtasun, and R. Zemel.
Efficient graph generation with graph recurrent attention networks. In Advances in Neural
Information Processing Systems, pages 4257–4267, 2019.
[39] P. Liu, S. Chang, X. Huang, J. Tang, and J. C. K. Cheung. Contextualized non-local neural
networks for sequence learning. arXiv preprint arXiv:1811.08600, 2018.
[40] S. Liu, Y. Chen, X. Xie, J. K. Siow, and Y. Liu. Automatic code summarization via multi-
dimensional semantic fusing in gnn. arXiv preprint arXiv:2006.05405, 2020.
[41] W. Liu, J. He, and S.-F. Chang. Large graph construction for scalable semi-supervised learning.
In ICML, 2010.
[42] L. Lovász. Random walks on graphs: A survey. Department of Computer Science, Yale
University, 1994.
[43] Y. Ma, S. Wang, C. C. Aggarwal, and J. Tang. Graph convolutional networks with eigenpooling.
arXiv preprint arXiv:1904.13107, 2019.
[44] H. V. Nguyen and L. Bai. Cosine similarity metric learning for face verification. In Asian
conference on computer vision, pages 709–720. Springer, 2010.
[45] W. Norcliffe-Brown, S. Vafeias, and S. Parisot. Learning conditioned graph structures for
interpretable visual question answering. In Advances in Neural Information Processing Systems,
pages 8344–8353, 2018.
[46] B. Pang and L. Lee. A sentimental education: Sentiment analysis using subjectivity summariza-
tion based on minimum cuts. In Proceedings of the 42nd annual meeting on Association for
Computational Linguistics, page 271. Association for Computational Linguistics, 2004.
[47] B. Samanta, A. De, N. Ganguly, and M. Gomez-Rodriguez. Designing random graph mod-
els using variational autoencoders with applications to chemical design. arXiv preprint
arXiv:1802.05283, 2018.
[48] P. Sen, G. Namata, M. Bilgic, L. Getoor, B. Galligher, and T. Eliassi-Rad. Collective classifica-
tion in network data. AI magazine, 29(3):93–93, 2008.
[49] C. Shi, M. Xu, Z. Zhu, W. Zhang, M. Zhang, and J. Tang. Graphaf: a flow-based autoregressive
model for molecular graph generation. arXiv preprint arXiv:2001.09382, 2020.
[50] L. Sun, Y. Dou, C. Yang, J. Wang, P. S. Yu, and B. Li. Adversarial attack and defense on graph
data: A survey. arXiv preprint arXiv:1812.10528, 2018.
[51] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, and
I. Polosukhin. Attention is all you need. In Advances in neural information processing systems,
pages 5998–6008, 2017.
[52] P. Veliˇckovi ́c, G. Cucurull, A. Casanova, A. Romero, P. Liò, and Y. Bengio. Graph attention
networks. arXiv preprint arXiv:1710.10903, 2017.
[53] Y. Wang, Z. Zhao, and Z. Feng. Graspel: Graph spectral learning at scale. arXiv preprint
arXiv:1911.10373, 2019.
[54] N. Wojke and A. Bewley. Deep cosine metric learning for person re-identification. In 2018
IEEE winter conference on applications of computer vision (WACV), pages 748–756. IEEE,
2018.
[55] L. Wu, I. E.-H. Yen, Z. Zhang, K. Xu, L. Zhao, X. Peng, Y. Xia, and C. Aggarwal. Scalable global
alignment graph kernel using random features: From node embedding to graph embedding. In
Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery &
Data Mining, pages 1418–1428, 2019.
[56] K. Xu, C. Li, Y. Tian, T. Sonobe, K.-i. Kawarabayashi, and S. Jegelka. Representation learning
on graphs with jumping knowledge networks. arXiv preprint arXiv:1806.03536, 2018.
[57] K. Xu, L. Wu, Z. Wang, and V. Sheinin. Graph2seq: Graph to sequence learning with attention-
based neural networks. arXiv preprint arXiv:1804.00823, 2018.
[58] K. Xu, L. Wu, Z. Wang, M. Yu, L. Chen, and V. Sheinin. Exploiting rich syntactic information
for semantic parsing with graph-to-sequence model. arXiv preprint arXiv:1808.07624, 2018.
[59] D.-Y. Yeung and H. Chang. A kernel approach for semisupervised metric learning. IEEE
Transactions on Neural Networks, 18(1):141–149, 2007.
[60] Z. Ying, J. You, C. Morris, X. Ren, W. Hamilton, and J. Leskovec. Hierarchical graph repre-
sentation learning with differentiable pooling. In Advances in Neural Information Processing
Systems, pages 4800–4810, 2018.
[61] J. You, R. Ying, X. Ren, W. L. Hamilton, and J. Leskovec. Graphrnn: Generating realistic
graphs with deep auto-regressive models. arXiv preprint arXiv:1802.08773, 2018.
[62] Y. Yu, J. Chen, T. Gao, and M. Yu. Dag-gnn: Dag structure learning with graph neural networks.
arXiv preprint arXiv:1904.10098, 2019.
[63] S. Yun, M. Jeong, R. Kim, J. Kang, and H. J. Kim. Graph transformer networks. In Advances
in Neural Information Processing Systems, pages 11960–11970, 2019.
[64] Y. Zhang, S. Pal, M. Coates, and D. Ustebay. Bayesian graph convolutional neural networks for
semi-supervised classification. In Proceedings of the AAAI Conference on Artificial Intelligence,
volume 33, pages 5829–5836, 2019.
[65] C. Zheng, B. Zong, W. Cheng, D. Song, J. Ni, W. Yu, H. Chen, and W. Wang. Robust graph
representation learning via neural sparsification. In ICML, 2020.
[66] X. Zheng, B. Aragam, P. K. Ravikumar, and E. P. Xing. Dags with no tears: Continuous
optimization for structure learning. In Advances in Neural Information Processing Systems,
pages 9472–9483, 2018