遗传算法
目录
一、算法原理
二、代码实现
三、结果分析
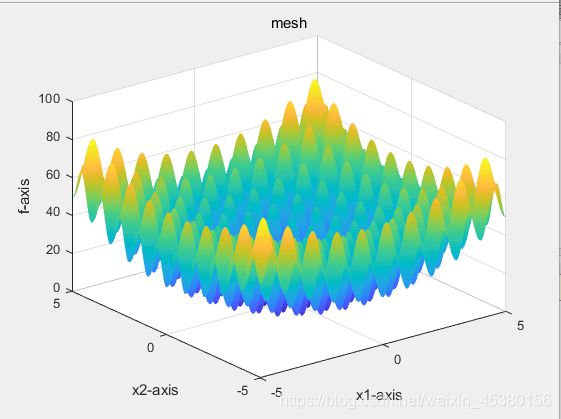
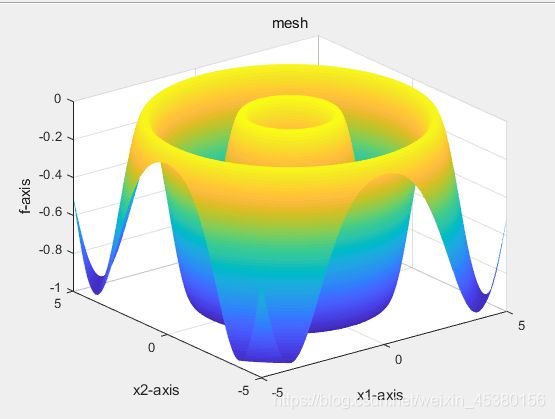
优化目标函数为Rastrigin(x)
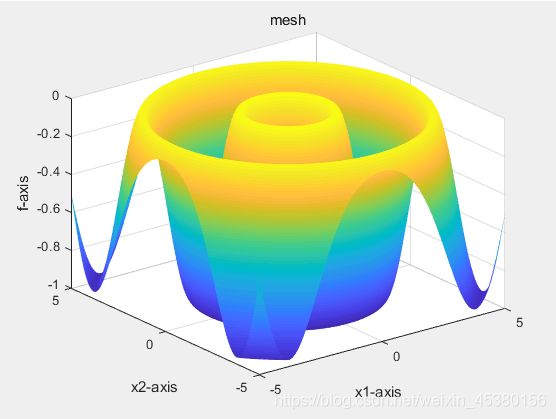
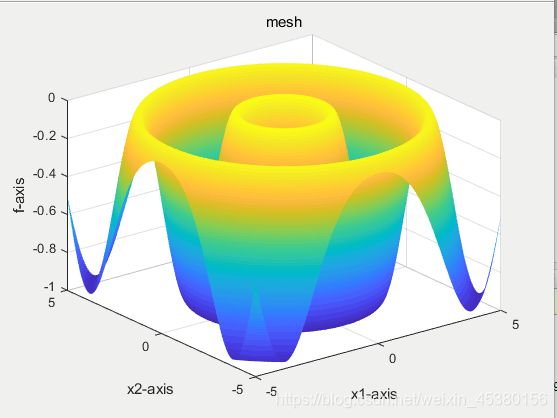
目标函数为Schaffer(x)
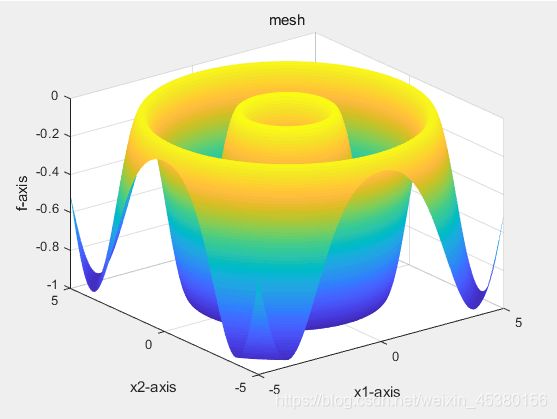
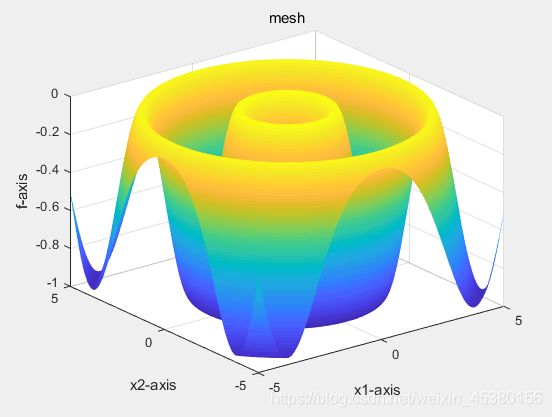
目标函数为Griewank(x)
总结
一、算法原理
1、基本原理
遗传算法是一种典型的启发式算法,属于非数值算法范畴。其目的是抽象和严谨地解释自然界的适应过程以及将自然生物系统的重要机理运用到人工系统的设计中。它是模拟达尔文的自然选择学说和自然界的生物进化过程的一种计算模型。它是采用简单的编码技术来表示各种复杂的结构,并通过对一组编码表示进行简单的遗传操作和优胜劣汰的自然选择来指导学习和确定搜索的方向。遗传算法的操作对象是一群二进制串(称为染色体、个体),即种群,每一个染色体都对应问题的一个解。从初始种群出发,采用基于适应度函数的选择策略在当前种群中选择个体,使用杂交和变异来产生下一代种群。如此模仿生命的进化进行不断演化,直到满足期望的终止条件。
- 种群:种群是指用遗传算法求解问题是,初始给定的多个解的集合。遗传算法的求解过程是从这个子集开始的。
- 个体:个体是指种群中的单个元素,它通常由一个用于描述其基本遗传结构的数据结构来表示。
- 染色体:染色体是指对个体进行编码后所得到的编码串。
- 适应度函数:适应度函数是一种用来对种群中各个个体的环境适应性进行度量的函数。其函数值是遗传算法实现优胜劣汰的主要依据
- 遗传操作:遗传操作是指作用于种群而产生新的种群的操作。标准的遗传操作有选择、杂交、变异。
2、算法步骤
(1)对遗传算法的运行参数进行赋值。参数包括种群规模、变量个数、交叉概率、变异概
率以及遗传运算的终止进化代数。
(2)建立区域描述器。根据轨道交通与常规公交运营协调模型的求解变量的约束条件,设置变量的取值范围。
(3)在(2)的变量取值范围内,随机产生初始群体,代入适应度函数计算其适应度值。
(4)执行比例选择算子进行选择操作。
(5)按交叉概率对交叉算子执行交叉操作。
(6)按变异概率执行离散变异操作。
(7)计算(6)得到局部最优解中每个个体的适应值,并执行最优个体保存策略。
(8)判断是否满足遗传运算的终止进化代数,不满足则返回(4),满足则输出运算结果。
3、流程图
二、代码实现
- 主要函数 GA.m
clc;clear all;
format long;%设定数据显示格式
%初始化参数
T=500;%仿真代数
N=80;% 群体规模
pm=0.05;pc=0.8;%交叉变异概率
umax=30;umin=-30;%参数取值范围
L=10;%单个参数字串长度,总编码长度Dim*L
Dim=5; %Dim维空间搜索
bval=round(rand(N,Dim*L));%初始种群,round函数为四舍五入
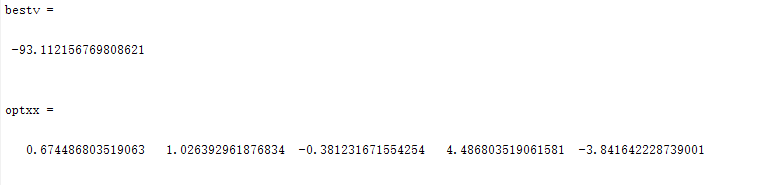
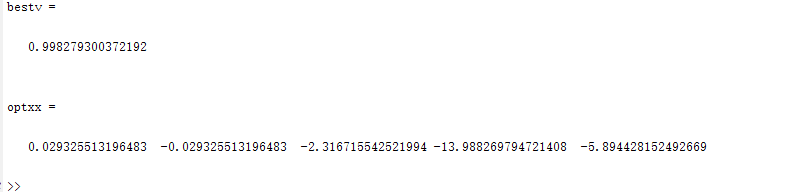
bestv=-inf;%最优适应度初值
funlabel=1; %选择待优化的函数,1为Rastrigin,2为Schaffer,3为Griewank
Drawfunc(funlabel);%画出待优化的函数,只画出二维情况作为可视化输出
%迭代开始
for ii=1:T
%解码,计算适应度
for i=1:N %对每一代的第i个粒子
for k=1:Dim
y(k)=0;
for j=1:1:L %从1到L,每次加以1
y(k)=y(k)+bval(i,k*L-j+1)*2^(j-1);%把第i个粒子转化为十进制的值,例如y1是第一维
end
x(k)=(umax-umin)*y(k)/(2^L-1)+umin;%转化为实际的x1
end
% obj(i)=100*(x1*x1-x2).^2+(1-x1).^2; %目标函数
obj(i)=fun(x,funlabel);
xx(i,:)=x;
end
func=obj;%目标函数转换为适应度函数
p=func./sum(func);
q=cumsum(p);%累加
[fmax,indmax]=max(func);%求当代最佳个体
if fmax>=bestv
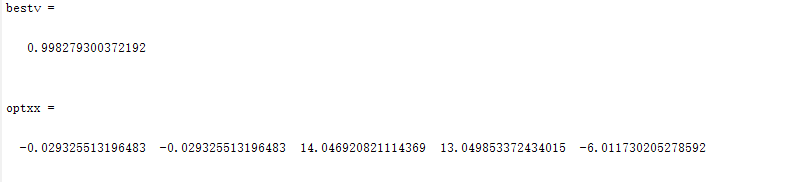
bestv=fmax;%到目前为止最优适应度值
bvalxx=bval(indmax,:);%到目前为止最佳位串
optxx=xx(indmax,:);%到目前为止最优参数
end
Bfit1(ii)=bestv; % 存储每代的最优适应度
%%%%遗传操作开始
%轮盘赌选择
for i=1:(N-1)
r=rand;
tmp=find(r<=q);
newbval(i,:)=bval(tmp(1),:);
end
newbval(N,:)=bvalxx;%最优保留
bval=newbval;
%单点交叉
for i=1:2:(N-1)
cc=rand;
if cc- fun.m,函数用于计算粒子适应度值
function y = fun(x,label)
%函数用于计算粒子适应度值
%x input 输入粒子
%y output 粒子适应度值
if label==1
y=-Rastrigin(x);
elseif label==2
y=-Schaffer(x);
else
y=-Griewank(x);
end- Rastrigin.m
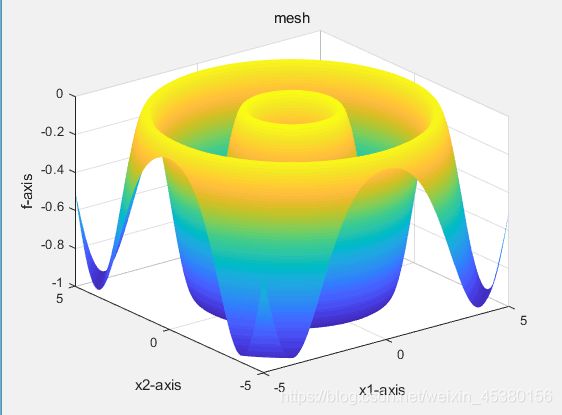
function y = Rastrigin(x)
% Rastrigin函数
% 输入x,给出相应的y值,在x = ( 0 , 0 ,…, 0 )处有全局极小点0.
% 编制人:
% 编制日期:
[row,col] = size(x);
if row > 1
error( ' 输入的参数错误 ' );
end
y =sum(x.^2-10*cos(2*pi*x)+10);
%y =-y;- Schaffer.m
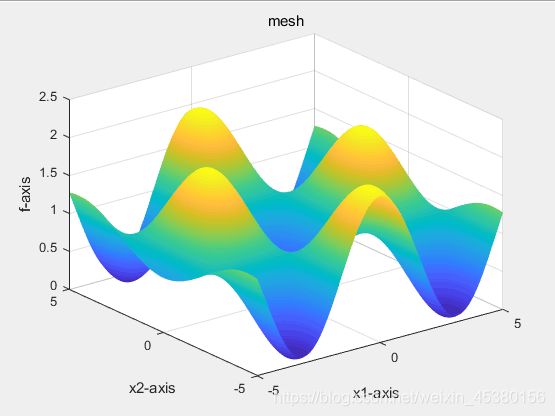
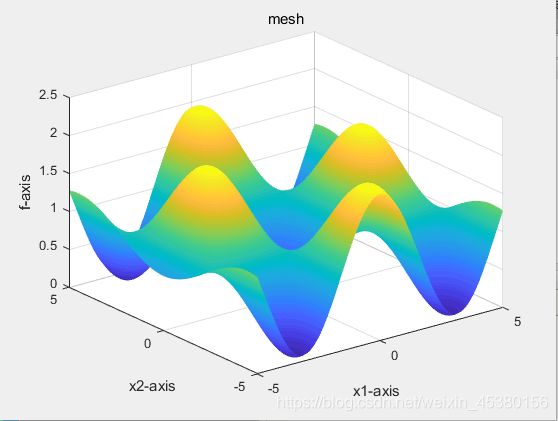
function y=Schaffer(x)
[row,col]=size(x);
if row>1
error('输入的参数错误');
end
y1=x(1,1);
y2=x(1,2);
temp=y1^2+y2^2;
y=0.5-(sin(sqrt(temp))^2-0.5)/(1+0.001*temp)^2;
y=-y;- Griewank.m
function y=Griewank(x)
%Griewan函数
%输入x,给出相应的y值,在x=(0,0,…,0)处有全局极小点0.
%编制人:
%编制日期:
[row,col]=size(x);
if row>1
error('输入的参数错误');
end
y1=1/4000*sum(x.^2);
y2=1;
for h=1:col
y2=y2*cos(x(h)/sqrt(h));
end
y=y1-y2+1;
%y=-y;
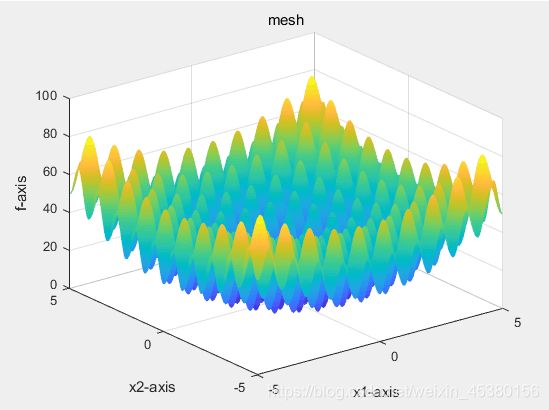
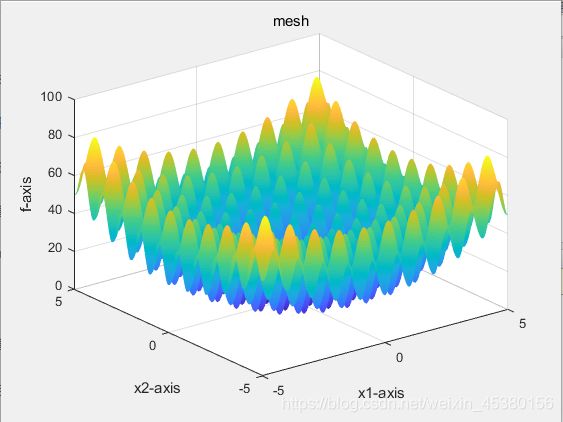
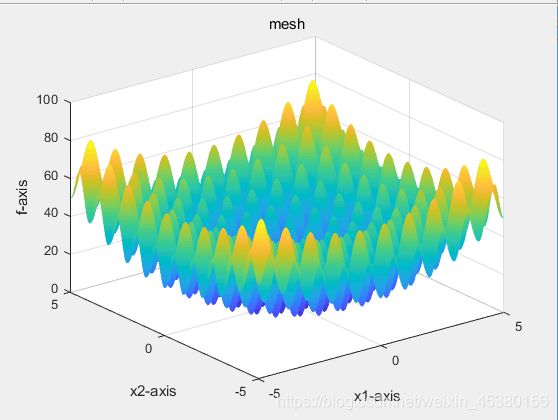
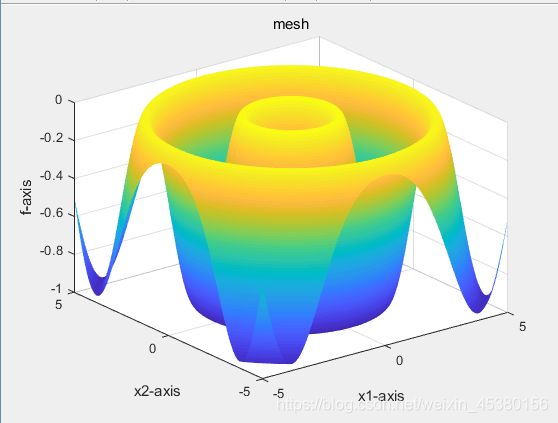
- Drawfunc.m
function Drawfunc(label)
x=-5:0.05:5;%41列的向量
if label==1
y = x;
[X,Y] = meshgrid(x,y);
[row,col] = size(X);
for l = 1 :col
for h = 1 :row
z(h,l) = Rastrigin([X(h,l),Y(h,l)]);
end
end
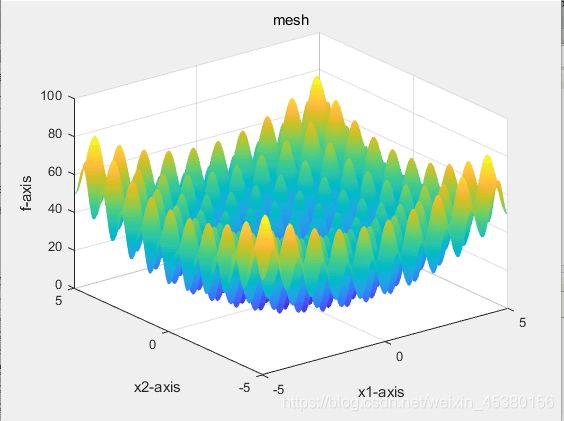
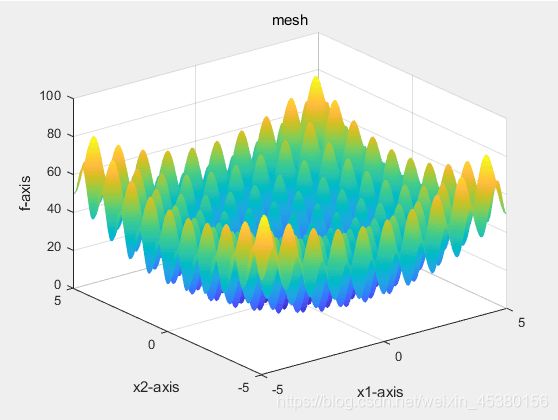
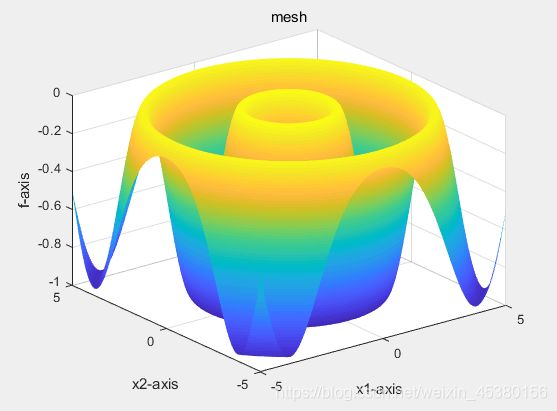
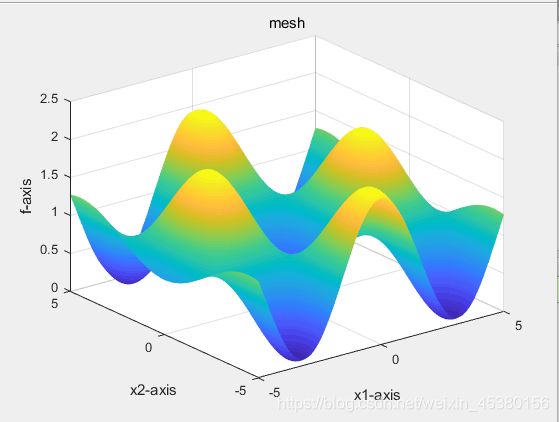
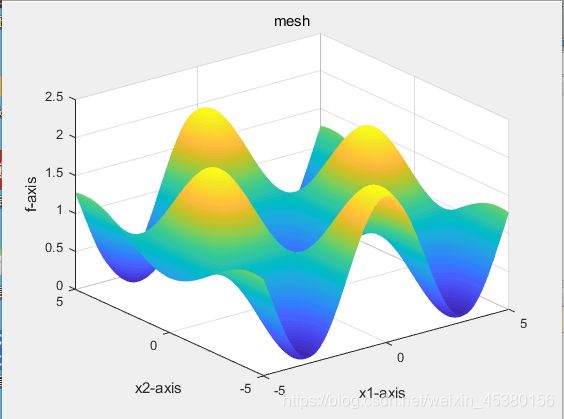
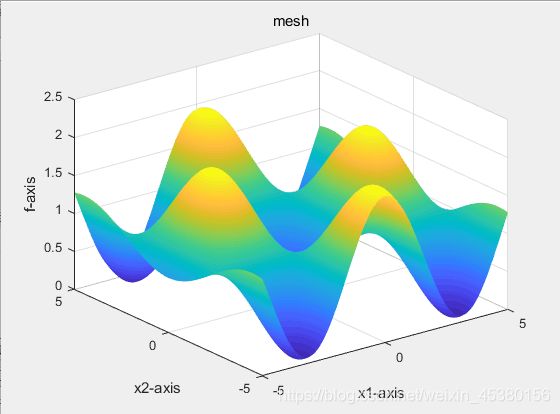
surf(X,Y,z);
shading interp
xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis');
title('mesh');
end
if label==2
y = x;
[X,Y] = meshgrid(x,y);
[row,col] = size(X);
for l = 1 :col
for h = 1 :row
z(h,l) = Schaffer([X(h,l),Y(h,l)]);
end
end
surf(X,Y,z);
shading interp
xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis');
title('mesh');
end
if label==3
y = x;
[X,Y] = meshgrid(x,y);
[row,col] = size(X);
for l = 1 :col
for h = 1 :row
z(h,l) = Griewank([X(h,l),Y(h,l)]);
end
end
surf(X,Y,z);
shading interp
xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis');
title('mesh');
end
三、结果分析
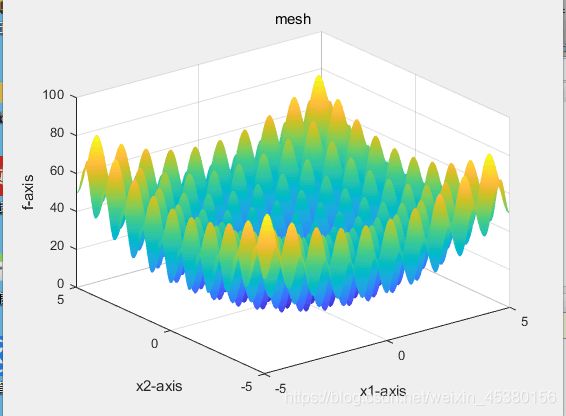
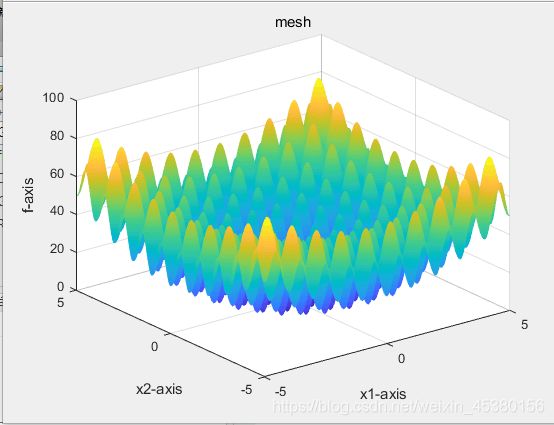
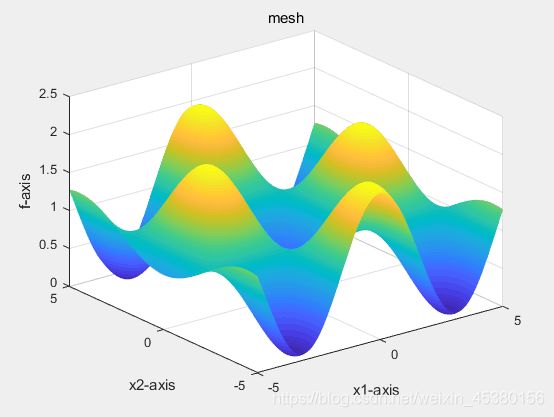
优化目标函数为Rastrigin(x)
- 空间维度Dim=2
种群数量N=10时:
种群数量N=40时:
种群数量N=80时:
种群数量N=140时:
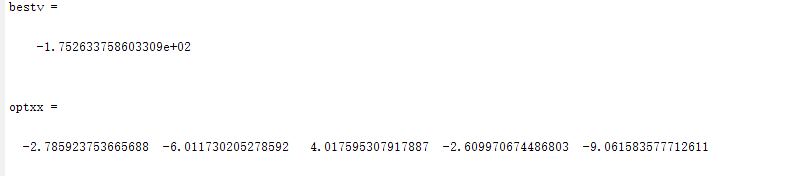
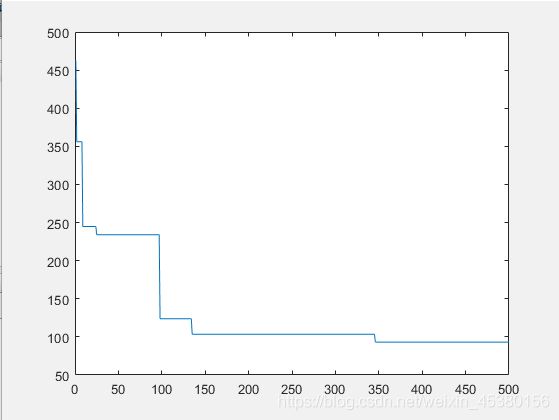
- 空间维度Dim=5
种群数量N=10时:
种群数量N=40时:
种群数量N=80时:
种群数量N=140时:
- 空间维度Dim=10,
种群数量N=10时
种群数量N=40时,
种群数量N=80时,
种群数量N=140时,
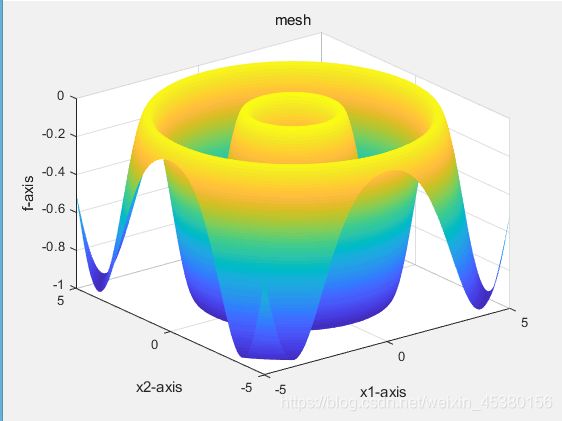
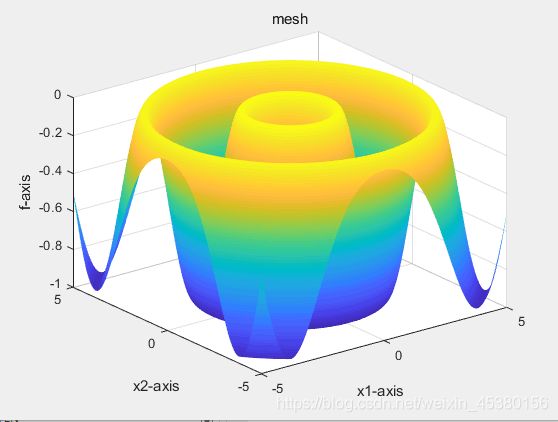
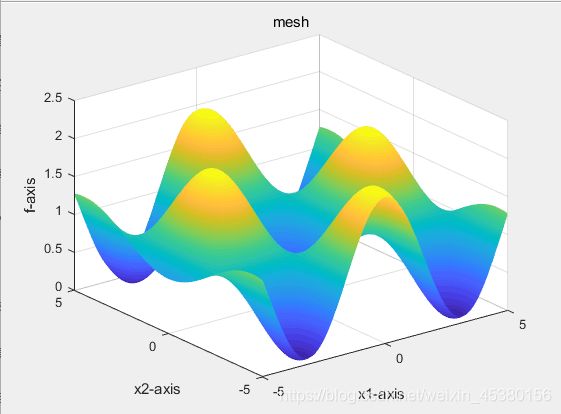
目标函数为Schaffer(x)
- 空间维度Dim=2
种群数量N=10,
种群数量N=40,
种群数量N=80,
种群数量N=140,
- 空间维度Dim=5
种群数量N=10,
种群数量N=40,
种群数量N=80,
种群数量N=140,
- 空间维度Dim=10
种群数量N=10,
种群数量N=40,
种群数量N=80,
种群数量N=140,
目标函数为Griewank(x)
- 空间维度Dim=2
种群数量N=10,
种群数量N=40,
种群数量N=80,
种群数量N=140,
- 空间维度Dim=5
种群数量N=10,
种群数量N=40,
种群数量N=80,
种群数量N=140,
- 空间维度Dim=10
种群数量N=10,
种群数量N=40,
种群数量N=80,
种群数量N=140,
总结
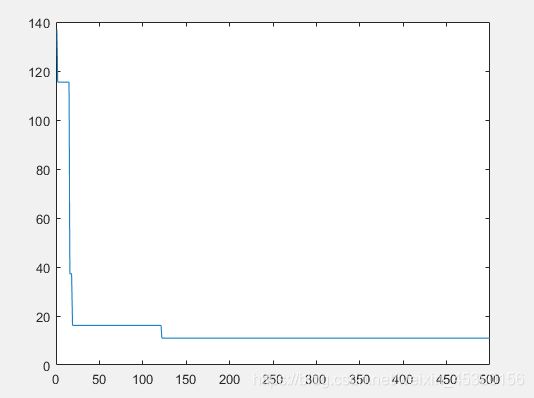
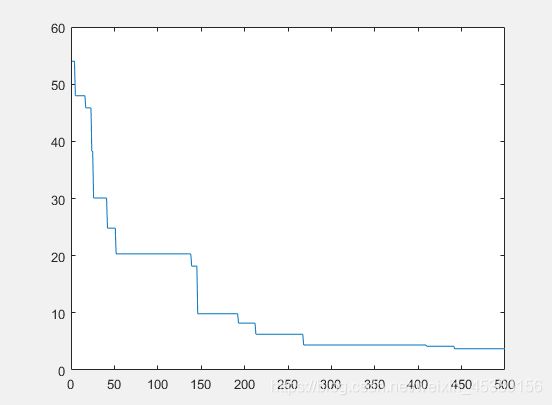
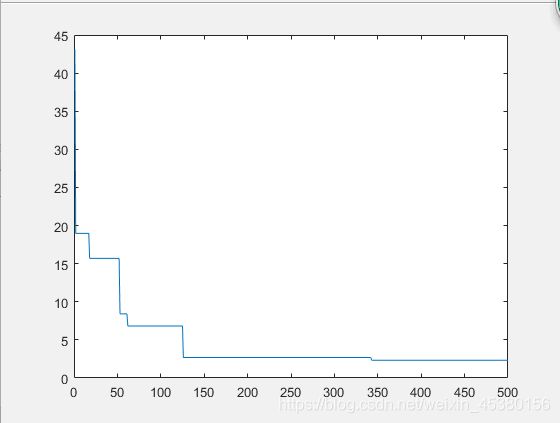
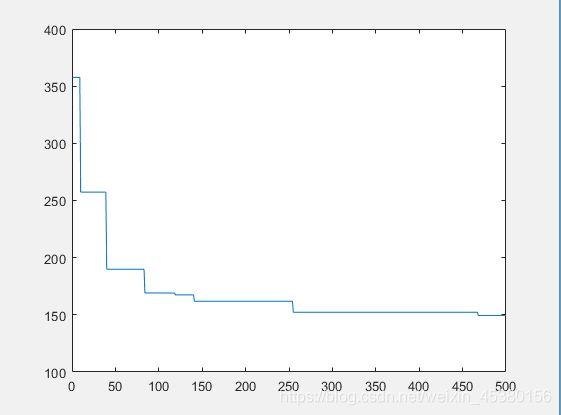
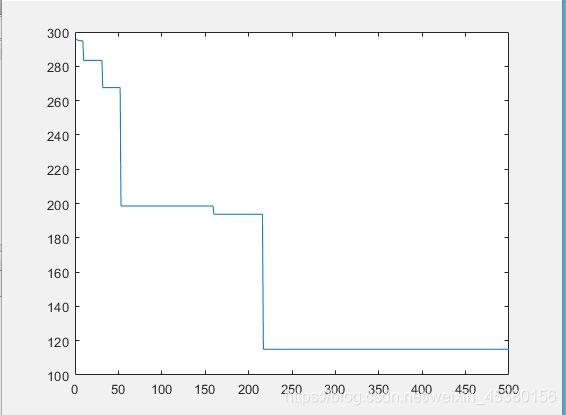
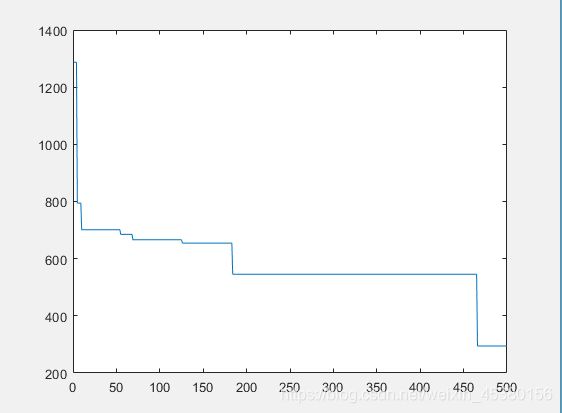
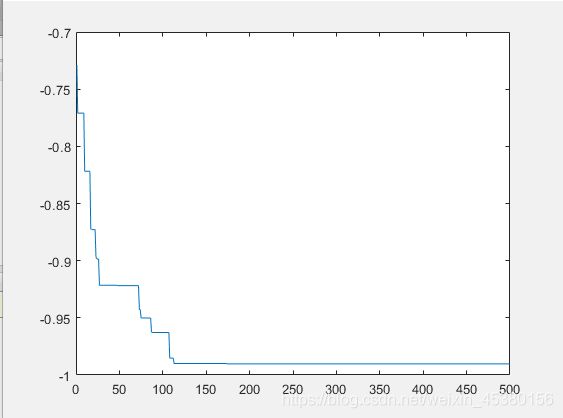
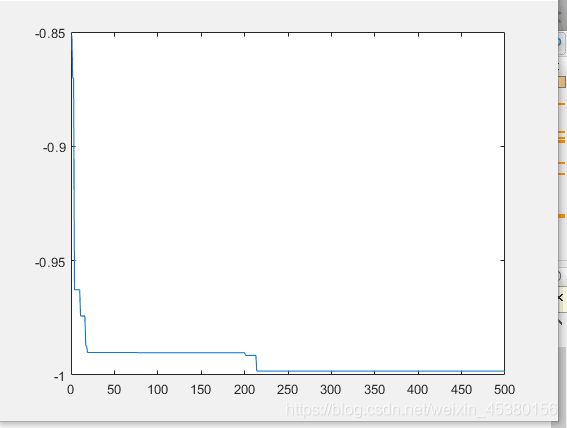
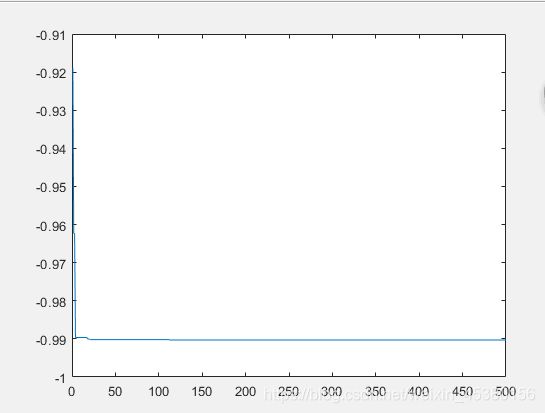
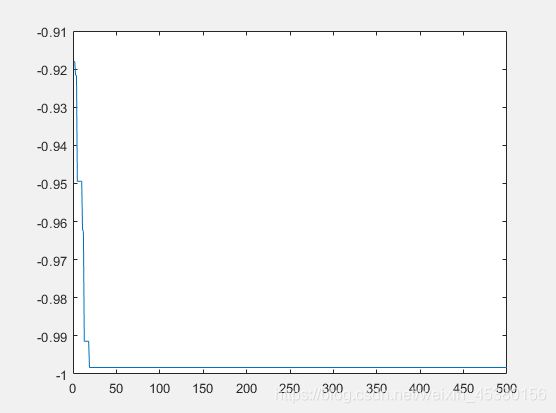
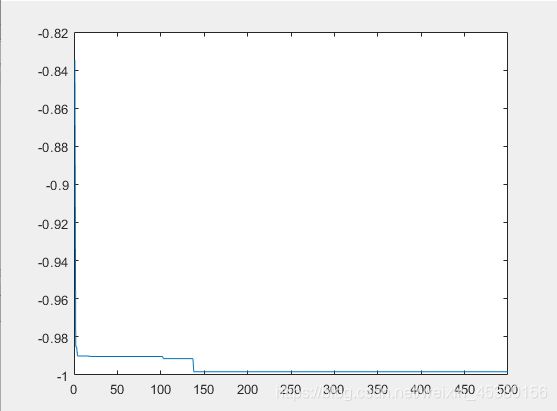
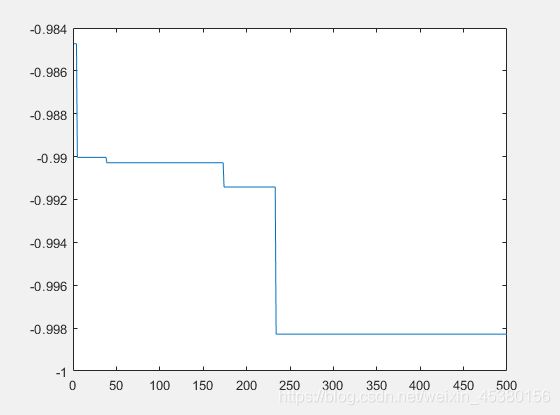
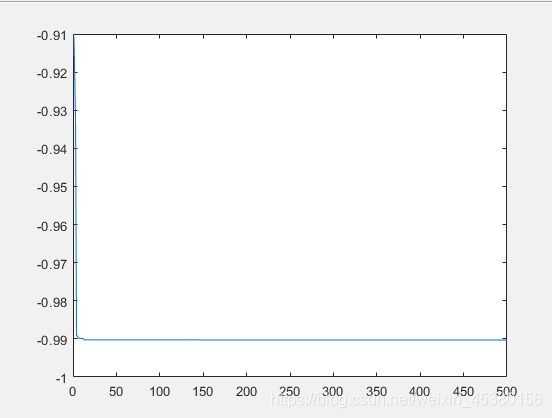
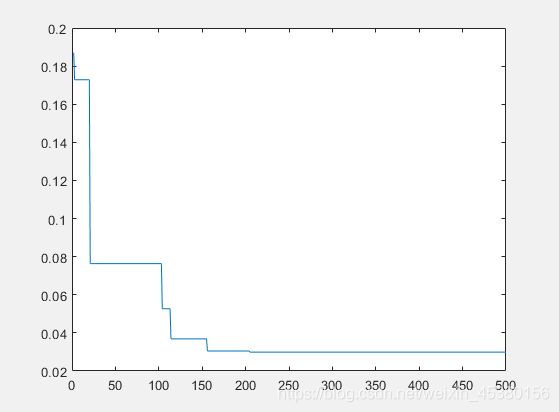
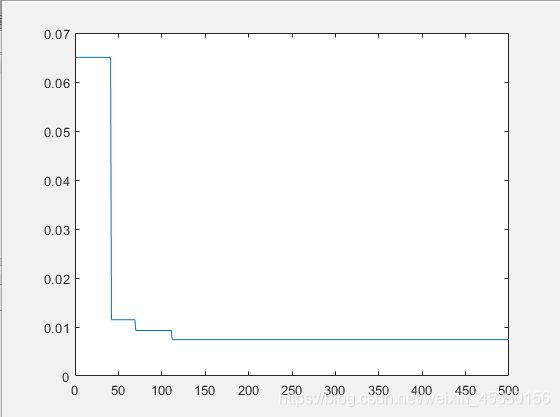
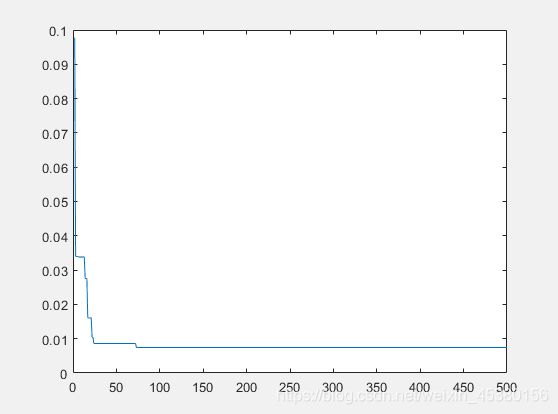
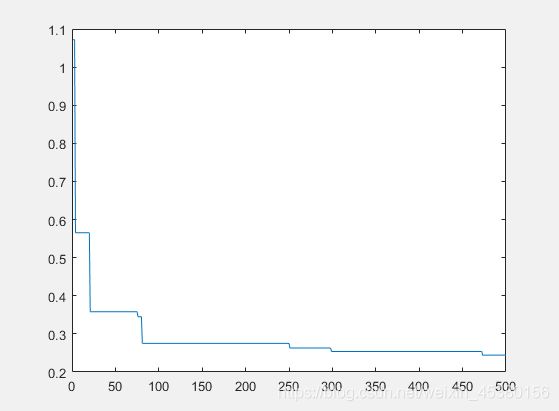
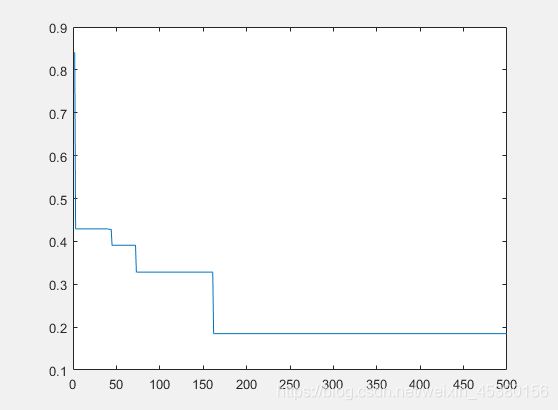
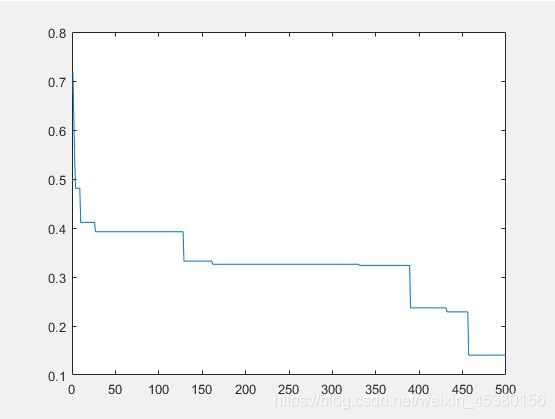
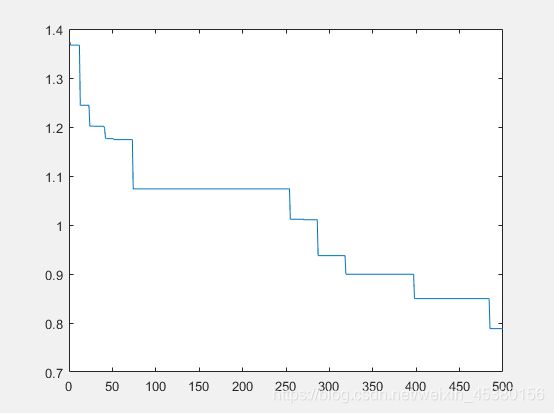
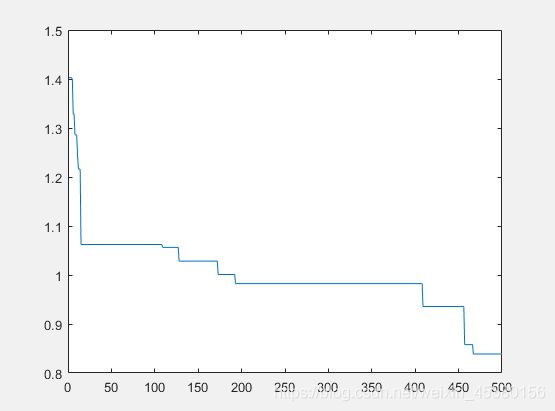
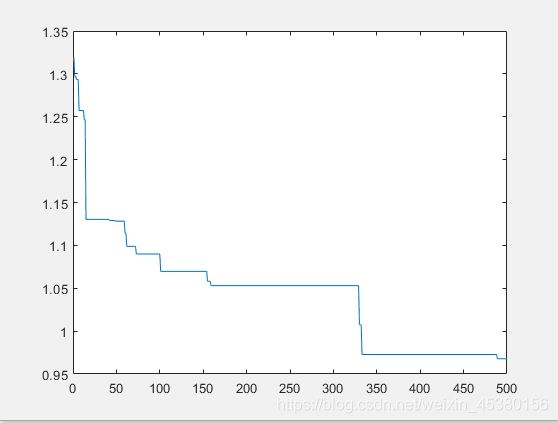
在上面的实验中,三个目标函数优化,每个函数当空间搜索维度Dim分别等于2,5,10时,分别分析种群数量N为10,40,80,140时最优适应度进化曲线的变化,发现以下:
当空间维度一定时,若种群数量N设置较大,一次进化所覆盖的模式较多,可以保证群体的多样性,从而提高算法的搜索能力;若N设置较小,虽降低了计算量,但是同时降低了每次进化中群体包含更多较好染色体的能力。