背包问题-动态规划
背包问题
通过观看b站up主大雪菜的视频,把九个背包问题进行学习,并记下笔记
分类:
- 01背包(只有选和不选)
- 完全背包(背包容量无限制)
- 多重背包(物品选的次数有限制)
- 混合背包
- 二维费用背包(两个限制)
- 分组背包问题(物体分组,每组只能选一个物体)
- 背包问题求方案数
- 求背包问题的方案(最优方案)
- 有依赖的背包问题(物品之间有依赖,有限制)
1、01背包问题:
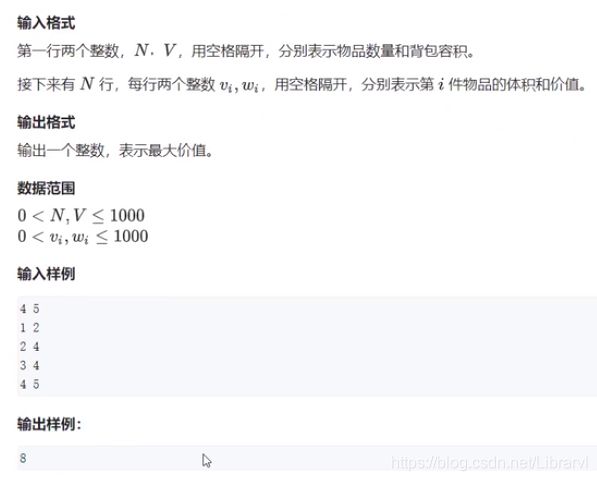
有 N 件物品和一个容量为 V 的背包
第 i 件物品的体积是 vi, 价值是 wi。
求解:将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值
背包问题,动态规划思路思考:
题目示例要求:在背包容量 5,共有 4 件可选物品时,如何选择使得背包中所装物品价值最大
思考角度:
- 从后往前思考,背包容量为 5 时,我可选 4 件物品,分成 4 种情况。
- 每种情况 背包容量和可选物品都相应减少,但是在上述中 4 种情况下的每一种情况都会新分出 3 中可选选项
- 这里可以用递归将其计算出来,但是过程中有许多重复计算。比如先选第2件再选第3件和先选第3件再选第2件的结果是一样的,不过计算了两次
- 我们发现如果之前选择情况已经达到最优,我们只需要在剩余背包容量允许的情况下,把价值最大的物品加入进来,就可以得到最优结果。
通过上述分析(第4条),我们已经将大问题分解成了重复的小问题,完成了划分状态
所以现在我们需要找到合适的 状态表示:
通过题意可以很容易的发现:
目标为最大价值,目标函数设为 f
其中题目给了两个变量,对应函数需要两个参数,一个是可选择的物品 i,和背包容量(V,这里我们用 j 表示,因为 背包容量在计算过程中不断变化)。
即在前 i 个可选物品,背包容量为 j 时,求 f 最大值。
即状态表示:f[i][j]
关键问题:状态转移
从思路分析中第 4 条可知:
物品是否可选。
-
可选:此时在前 i 个物品,背包容量为 j 时,此时价值为
f[i][j]。而此状态应该是在前i 个物品,背包容量为j - v[i]时的最优选择,加上 第 i 个物品的价值f[i][j] = f[i - 1][j - v[i]] + w[i] -
不可选(背包放不下):
f[i][j] = f[i - 1][j]
判优:使得 max(f[i][j]),
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i])
边界条件:
初始状态:f[0][0] = 0
结束条件:遍历完所有状态,前 i 个物品,总体积为 j 时的最优价值
总结:
时间复杂度:O(n^2),空间复杂度:O(n^2)
f[i][j] :前 i 个物品,总体积是 j 的情况下的总价值
result = max(f[n][0 ~ v])
f[i][j]:
1. 不选第 i 个物品, f[i][j] = f[i - 1][j]
2.选第 i 个物品, f[i][j] = f[i - 1][j - v[i]] + w[i];
f[i][j] = max{情况1,情况2}
初始状态:
f[0][0] = 0;
代码:
#include
#include
#include
using namespace std;
const int N = 1010;
int n, m;
int f[N][N]; // 价值
int v[N]; // 每个物品的体积,全局变量定义到堆空间,则默认全为 0
int w[N]; // 每个物品的价值
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
if(j < v[i]) // 如果装不下,就不装和上一个状态一样
f[i][j] = f[i - 1][j];
else if(j >= v[i]) // 只有 容量 > 当前物品体积,才能放入
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
cout << f[n][m];
return 0;
}
执行过程
| j = 0 | j = 1 | j = 2 | j = 3 | j = 4 | j = 5 | |
|---|---|---|---|---|---|---|
| i = 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i = 1(v = 1) | 0 | |||||
| i = 2(v = 2) | 0 | |||||
| i = 3(v = 3) | 0 | |||||
| i = 4(v = 4) | 0 |
按行遍历,含义:在 前 1 件物品,背包容量从 1~5 时,每一种情况的最优解
| j = 0 | j = 1 | j = 2 | j = 3 | j = 4 | j = 5 | |
|---|---|---|---|---|---|---|
| i = 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i = 1 | 0 | 2 | 2 | 2 | 2 | 2 |
| i = 2 | 0 | |||||
| i = 3 | 0 | |||||
| i = 4 | 0 |
从程序中挑选
在 i = 2 ,j = 3 时,说明在前两件物品(第一件 体积 1,价值 2;第二件 体积 2,价值 4)时状态f[2][3]取决于
f[2-1][j - v[2]](f[1][1])加上 w[2],含义是 在前 1 件物品可选,背包容量为 1 时,最优状态(只取第一件物品 2)加上第二件物品(因为 背包中正好空出 2 体积,可以放下 第二件物品)的状态
f[2][3] = f[2-1][j - v[2]] +w[2] = 2 + 4 = 6。所以状态更新为
| j = 0 | j = 1 | j = 2 | j = 3 | j = 4 | j = 5 | |
|---|---|---|---|---|---|---|
| i = 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i = 1 | 0 | 2 | 2 | 2 | 2 | 2 |
| i = 2 | 0 | 2 | 4 | 6 | ||
| i = 3 | 0 | |||||
| i = 4 | 0 |
比如上述 (i = 2, j = 2)时,装不下 物品 2,所以需要需要在不选和选之间做一个最优判断
即:
- 不选
f1 = f[1][2] = 2,只放 第一件物品 - 选
f2 = f[1 -1][2 -2] + 4 = 4, 即将 物品 1 拿出,放入 物品 2 f[2][2] = max(f1, f2) = 4
优化:
由于每一次只用了上一个的数据,即f[i - 1][j - v[i]] + w[i],就是说只用了上一层的v[i]
所以可以用一维数据进行保存,不断刷新此数组就可以利用 “上一层”数据。
同时也需要注意的一点是 j 必须从大到小遍历 因为我们需要j - v[i]“之前的数据”。同时通过j >= v[i]达到了判断是否可选的问题
时间复杂度:O(n^2),空间复杂度:O(n)
#include
#include
using namespace std;
const int N = 1010;
int n, m;
int f[N]; // 价值
int v[N]; // 每个物品的体积,全局变量定义到堆空间,则默认全为 0
int w[N]; // 每个物品的价值
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = m; j >= v[i]; j--) // 从大到小枚举
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m];
return 0;
}
| j = 1 | j = 2 | j = 3 | j = 4 | j = 5 | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| i= 1 | 0+2 = 2 | 0+2 = 2 | 0+2 = 2 | 0+2 = 2 | 0+2 = 2 |
| i= 2 | 2 | 4 | 2 + 4 = 6 | 2 + 4 = 6 | 2 + 4 = 6 |
| i= 3 | 2 | 4 | 6 | 2 + 4 = 6 | 4 + 4 =8 |
| i= 4 | 2 | 4 | 6 | 6(0 + 5 = 5) | 8(2 + 5 = 7) |
更新方向: 《================================================================
从上表可以看出来,每一次的一维矩阵的刷新过程。同时我们也可以知道为什么要从大到小来遍历,是因为每次要满足f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i])中的f[i - 1]
保证遍历是用的是 i - 1,也就是 f[j - v[i]] + w[i] 等价 f[i - 1][j - v[i]] + w[i]
所以,从大到小遍历,保证了每个物品只用了一次
此问题解决在小于等于 m 时,最大价值是多少
如果考察恰好等于 m 时,最大价值,需要将 f[0] 初始化 0,其余都为 负无穷
2、完全背包问题
有 N 件物品和一个容量为 V 的背包,每种物品都有无限件可用。
第 i 间物品的体积是 vi, 价值是 wi。
求解:将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值
思路
f[i]:总体积是 i 的情况下,最大价值是多少
result = max(f[0 ~ m])
通过上一个01背包简化问题分析,对于完全背包问题,只需要将
for(int j = m; j >= v[i]; j--) // 从大到小 遍历
改为
for(int j = v[i]; j <= m; j++) // 从小到大 遍历
本质上不需要从大到小遍历保证每次迭代都是用的第 i-1 个物品。而完全背包只要背包内有容量,该物品就可以一直想包里放,从v[i]~m次试验,也就是经过多次f[j - v[i]] + w[i],所以达到了只要包内有空闲地方就可以向包中加
举例说明
| j = 1 | j = 2 | j = 3 | j = 4 | j = 5 | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| i = 1 | 0+2 = 2 | f[2-1]+w[1]=2+2 = 4 | f[3-1]+w[1]=4+2 = 6 | f[4-1]+w[1]=6+2 = 8 | f[5-1]+w[1]=8+2 = 10 |
更新方向: ========================================================》
所以由于更新方向的不同,在 物品 i 确定的情况下,每次 j 的增大,v[i] 都有机会加入其中
也就是 for(int j = v[i]; j <= m; j++)在执行过程中,会“经历”许多 v[i]
从数学上也可以证明:
如果按照原思路进行计算应该是
for(int i = 1; i <= n; i++)
{
for(int j = m; j >= v[i]; j--)
{
for(int k = 0; k * v[i] <= j; k++) // 选了几次
f[j] = max(f[j], f[j - k * v[i]] + K * w[i]);
}
}
从大到小来计算,必须要多加一层循环,将全为 物品 i 的情况计算一遍。
因为在物品 i 时,所有容量比 j 小的数,都没有算过。所以比 j 小的情况都没有包含 第 i 个物品。
所以 在 容量 j 允许的情况下,每次放入一个 v[i],加上一个 w[i],循环 k 次。
证明,数学归纳法:
1.假设考虑前 i- 1个物品之后,所有的 f[j] 都是正确的
2.来证明:考虑完第 i 个物品后,所有的 f[j] 也都是正确的
对于某个 j 而言,如果最优解中包含 k 个 v[i];
从小到大枚举,一定可以枚举到 f[j - k * v[i]],且f[j - k * v[i] - v[i]]背包内放不下,会保持原有数值f[j]
也就是 f[j - (k - 1) * v[i] - v[i]] + w[i] 中 (k - 1) * v[i] 的状态一定通过 f[j - k * v[i]] 来更新。而 f[j - k * v[i]] 为 完全不包含 第 i 物品的状态,也就是对应从小到大遍历时的初始情况
...以此类推
而 f[j] = max(f[j],f[j - v[i]] + w[i])中一定计算了 包含 v[i] 情况的数值,然后与原有 f[j] 作比较
所以
for(int j = m; j >= v[i]; j--)
{
for(int k = 0; k * v[i] <= j; k++) // 选了几次
f[j] = max(f[j], f[j - k * v[i]] + K * w[i]);
}
可以被替换为:
for(int j = v[i]; j <= m; j++) // 从小到大枚举
f[j] = max(f[j], f[j - v[i]] + w[i]);
代码:
#include
#include
#include
using namespace std;
const int N = 1010;
int n, m;
int f[N]; // 价值
int v[N]; // 每个物品的体积,全局变量定义到堆空间,则默认全为 0
int w[N]; // 每个物品的价值
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = v[i]; j <= m; j++) // 从小到大枚举
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m];
return 0;
}
3、多重背包问题
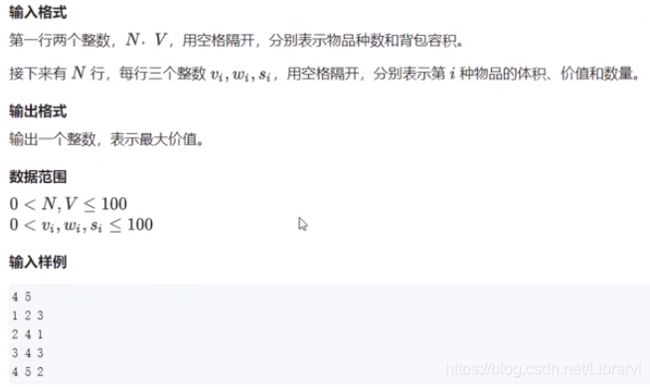
有 N 件物品和一个容量为 V 的背包,每种物品都有无限件可用。
第 i 间物品最多有 s 件,每件体积是 vi, 价值是 wi。
求解:将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值
思路:
f[i]:总体积是 i 的情况下,最大价值是多少
在状态转移时,加一层循环
for(int i = 1; i <= n; i++)
for(int j = m; j >= v[i]; j--) // 从大到小枚举
f[j] = max(f[j], f[j - v[i]] + w[i], f[j - 2 * v[i]] + 2 * w[i] ... );
1.f[i] = 0
result = f[m]
2.f[0] = 0, f[i] = -Inf, i != 0;
result = max(f[0 ~ m])
时间复杂度 O(n^3)
优化
1、多重背包的二进制优化方法。
思路:
将多重背包 -----> 01背包
1.每个物体拆成 s 个,重复 s 个,放入数组(复杂度也会超,此方法比较简单)
2.拆的方式:向上取整 log(s),没有分成 s 份,而是 log(s) 份
7
1 2 4
1
2
3 = 1 + 2
4
5 = 1 + 4
6 = 2 + 4
7 = 1 + 2 + 4
10
1 2 4 3 3 是 10 - 7 得到的,如果是 8,则会表达出大于10的数
代码:
#include
#include
using namespace std;
const int N = 2010;
int n, m;
int f[N]; // 价值
struct Good
{
int v, w;
};
int main()
{
vector goods;
cin >> n >> m;
for(int i = 1; i <= n; i++)
{
int v, w, s;
cin >> v >> w >> s;
for(int k = 1; k <= s; k *= 2)
{
s -= k;
goods.push_back({v*k, w*k});
}
if(s > 0) goods.push_back({v*s, w*s});
}
for(auto good: goods)
{
for(int j = m; j >= good.v; j--)
{
f[j] = max(f[j], f[j - good.v] + good.w);
}
}
cout << f[m];
return 0;
}
4、混合背包问题
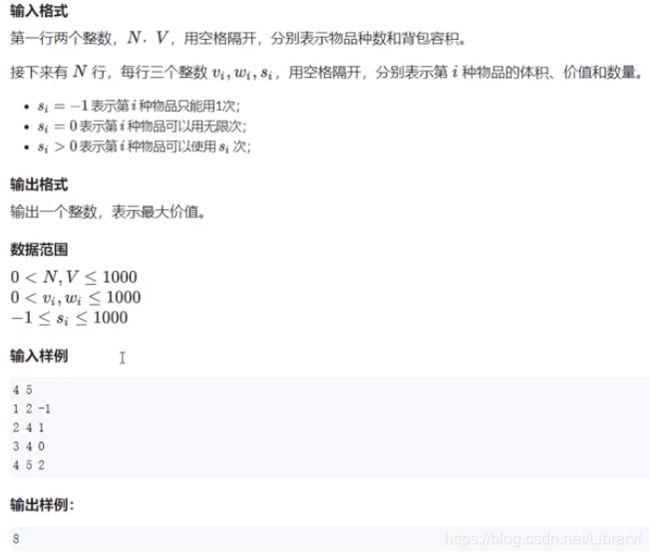
有 N 件物品和一个容量为 V 的背包。
物品一共有三类:
- 第一类物品只能用 1 次(01背包)
- 第二类物品能用无限次(完全背包)
- 第三类物品能用有限次(多重背包)
第 i 件物品的体积是 vi, 价值是 wi。
求解:将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值
思路:
第一二类:正常做
第三类:二进制优化
在做的时候进行判断,按照要求进行求解
#include
#include
using namespace std;
const int N = 1010;
int n, m;
int f[N];
struct Thing
{
int kind;
int v, w;
};
vector things;
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i++)
{
int v, w, s;
cin >> v >> w >> s;
if(s < 0)
things.push_back({-1, v, w});
else if(s == 0)
things.push_back({0, v, w});
else{
for(int k = 1; k <= s; k *= 2)
{
s -= k;
things.push_back({-1, v * k, w * k});
}
if(s > 0) things.push_back({-1, v * s, w * s});
}
}
for(auto thing : things)
{
if(thing.kind < 0)
{
for(int j = m; j >= thing.v; j--)
f[j] = max(f[j], f[j - thing.v] + thing.w);
}
else
{
for(int j = thing.v; j <= m; j++)
f[j] = max(f[j], f[j - thing.v] + thing.w);
}
}
cout << f[m] << endl;
return 0;
}
5、二维背包问题
有 N 件物品和一个容量为 V 的背包, 背包能承受的最大重量是 M
每件物品只能用一次,第 i 件物品的体积是 vi, 重量是mi,价值是 wi。
求解:将哪些物品装入背包,可使这些物品的总体积不超过背包容量,这些物品的总重量不超过背包所承受重量,且总价值最大。输出最大价值
思路
状态 f[i][j]:体积是 i, 重量是 j 的情况下,价值是多少
循环 1 层: 第 i 个物品
循环 2 层: 第 i 个物品的体积
循环 3 层: 第 i 个物品的重量
#include
#include
#include
using namespace std;
const int N = 110;
int n, v, m;
int f[N][N];
int main()
{
cin >> n >> v >> m;
for (int i = 0; i < n; i++)
{
int a, b, c;
cin >> a >> b >> c;
for (int j = v; j >= a; j--)
{
for (int k = m; k >= b; k--)
{
f[j][k] = max(f[j][k], f[j - a][k - b] + c);
}
}
}
cout << f[m] << endl;
return 0;
}
6、分组背包问题
有 N 件物品和一个容量为 V 的背包
每组物品有若干个,同一组内的物品最多只能选一个
第 i 件物品的体积是 vij,价值是 wij,其中 i 是组号,j 是组内编号。
求解:将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值
组内物品互斥
思路:
f[i][j] :前 i 个物品,总体积是 j 的情况下的总价值
每组的决策:s + 1种,选,或选哪个
for(int i = 0; i < n; i++) // 循环物品
{
for(ing j = m; j >= v; j--) // 循环体积
{
f[j] = max(f[j], f[j - v[0]] + w[0], f[j - v[1]] + w[1] ...)
}
}
代码:
#include
#include
using namespace std;
const int N = 110;
int n, m;
int f[N], v[N], w[N];
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i++)
{
int s;
cin >> s;
for(int j = 0; j < s; j++)
cin >> v[j] >> w[j];
for(int j = m; j >= 0; j--)
{
for(int k = 0; k < s; k ++)
{
if(j >= v[k])
f[j] = max(f[j],f[j - v[k]] + w[k]);
}
}
}
cout << f[m];
return 0;
}