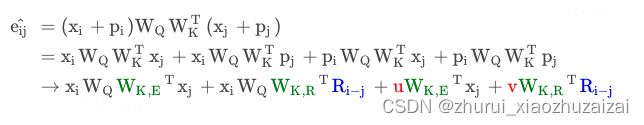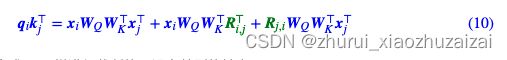绝对位置编码【三角/递归/相乘】->相对位置编码【XLNET/T5/DEBERTA】->旋转位置编码(ROPE/XPOS)->复杂位置编码【CNN/RNN/复数/融合】
Alibi 位置编码
主要是Bloom模型采用,Alibi 的方法也算较为粗暴,是直接作用在attention score中,给 attention score 加上一个预设好的偏置矩阵,相当于 q 和 k 相对位置差 1 就加上一个 -1 的偏置。其实相当于假设两个 token 距离越远那么相互贡献也就越低。
ALiBi的做法其实和T5 bias类似,直接给q*k attention score加上了一个线性的bias:KERPLE(Kernelized Relative Positional Embedding for Length Extrapolation)
KERPLE主要针对Alibi 做了一些微小改进,将内积的bias由之前自然数值幂函数或指数函数,并且改成可学习参数。
Sandwich(Receptive Field Alignment Enables Transformer Length Extrapolation)
Sandwich将ALiBi的线性bias改为正弦编码的内积pm*pn,上述编码也是对于正余弦三角式的一种改进。
XPOS(Extrapolatable Position Embedding)
XPOS可以看作是对RoPE的略微改进,在RoPE的内积基础上引入了一个指数衰减项,几何上,变换提供向量的旋转。 如果 q 和 k 之间的相对角度较大,则内积为更小。 然而,余弦值并不单调如果旋转角度大于π,这会导致一种不稳定的现象,期望内积随着相对距离的增长。
关于ALIBA等的位置编码与外推性的内容详见另一篇文章:
1 绝对位置编码
在输入的第k个向量xk中加入位置向量pk变为xk+pk,其中pk只依赖于位置编号k。
1.1 训练式
将位置编码当作可训练参数,比如最大长度为512,编码维度为768,那么就初始化一个512×768的矩阵作为位置向量,让它随着训练过程更新。现在的BERT、GPT等模型所用的就是这种位置编码,事实上它还可以追溯得更早,比如2017年Facebook的《Convolutional Sequence to Sequence Learning》就已经用到了它。
它的缺点是没有外推性,即如果预训练最大长度为512的话,那么最多就只能处理长度为512的句子,再长就处理不了了。
当然,也可以将超过512的位置向量随机初始化,然后继续微调。
最近的研究表明,通过层次分解的方式,可以使得绝对位置编码能外推到足够长的范围你n2,同时保持还不错的效果,细节请参考博文《层次分解位置编码,让BERT可以处理超长文本》。
构建一种位置编码的延拓方案,它跟原来的前n个编码相容,然后还能外推到更多的位置,剩下的就交给模型来适应了此外,讨论一下α的选取问题,苏神的实验默认的选择是α=0.4。
理论上来说,α∈(0,1)且α≠0.5都成立,但是从实际情况出发,还是建议选择0<α<0.5的数值。
因为我们很少机会碰到上万长度的序列,对于个人显卡来说,能处理到2048已经很壕了,
如果n=512,那么这就意味着i=1,2,3,4而j=1,2,⋯,512,
如果α>0.5的话,那么从分解式(1)看αui就会占主导,因次位置编码之间差异变小(因为i的候选值只有4个),模型不容易把各个位置区分开来,会导致收敛变慢;
如果α<0.5,那么占主导的是(1−α)uj,位置编码的区分度更好(j的候选值有512个),模型收敛更快一些。
优点:简单方便,无需额外开销
缺点:1.这样得到的位置编码是独立训练得到的,不同位置的编码向量没有明显的约束关系,因此只能建模绝对位置信息,不能建模不同位置之间的相对关系。
2.句子长度不能超出位置编码的范围
1.2 三角式
三角函数式位置编码,一般也称为Sinusoidal位置编码,是Google的论文《Attention is All You Need》所提出来的一个显式解:
很明显,三角函数式位置编码的特点是有显式的生成规律,因此可以期望于它有一定的外推性。
另外一个使用它的理由是:由于sin(α+β)=sinαcosβ+cosαsinβ以及cos(α+β)=cosαcosβ−sinαsinβ,这表明位置α+β的向量可以表示成位置α和位置β的向量组合,这提供了表达相对位置信息的可能性。
但很奇怪的是,现在我们很少能看到直接使用这种形式的绝对位置编码的工作,原因不详。
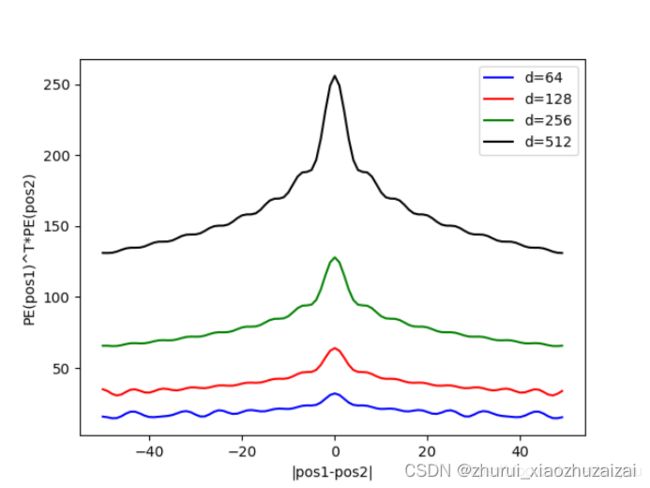
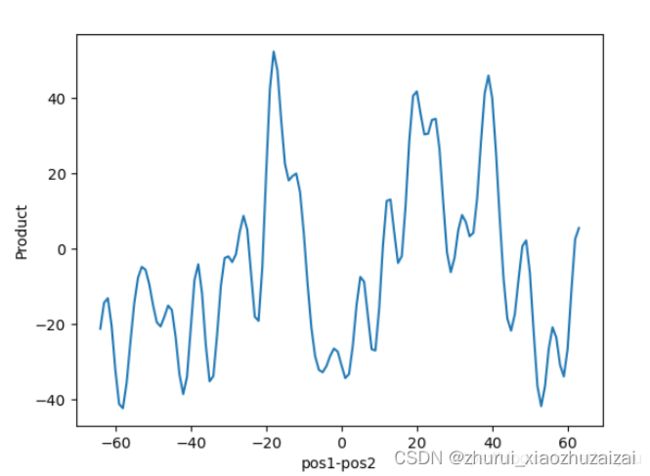
但这个的问题首先在于,cos是一个偶函数,也就是说pos1-pos2等于a或−a对位置相关性是没有影响的,但实际上,我们希望位置编码是可以区分前后的。因此真正使用的并不是PE_1TPE_2
Note:使用Sinusoidal Position Embedding和Learned Positional Embedding在实验表现上区别不大,因此后面的一些论文如BERT,处于简便性考虑,采用的是Learned Positional Embedding
1.3 递归式
原则上来说,RNN模型不需要位置编码,它在结构上就自带了学习到位置信息的可能性
同理,我们也可以用RNN模型来学习一种绝对位置编码,比如从一个向量p0出发,通过递归格式pk+1=f(pk)来得到各个位置的编码向量。
ICML 2020的论文《Learning to Encode Position for Transformer with Continuous Dynamical Model》把这个思想推到了极致,它提出了用微分方程(ODE)dpt/dt=h(pt,t)的方式来建模位置编码,该方案称之为FLOATER。显然,FLOATER也属于递归模型,函数h(pt,t)可以通过神经网络来建模,因此这种微分方程也称为神经微分方程,关于它的工作最近也逐渐多了起来。
理论上来说,基于递归模型的位置编码也具有比较好的外推性,同时它也比三角函数式的位置编码有更好的灵活性(比如容易证明三角函数式的位置编码就是FLOATER的某个特解)。但是很明显,递归形式的位置编码牺牲了一定的并行性,可能会带速度瓶颈。
1.4 相乘式
输入xk与绝对位置编码pk的组合方式一般是xk+pk,
对于融合两个向量有多种方式,相加、相乘甚至拼接都是可以考虑的,怎么大家在做绝对位置编码的时候,都默认只考虑相加了?
最近的一个实验显示,似乎将“加”换成“乘”,也就是xk⊗pk的方式,似乎比xk+pk能取得更好的结果。具体效果本人也没有完整对比过,只是提供这么一种可能性。关于实验来源,可以参考《中文语言模型研究:(1) 乘性位置编码》。
二 相对位置编码
Paper: Self-Attention with Relative Position Representations (Shaw et al.2018)
相对位置并没有完整建模每个输入的位置信息,而是在算Attention的时候考虑当前位置与被Attention的位置的相对距离,由于自然语言一般更依赖于相对位置,所以相对位置编码通常也有着优秀的表现。对于相对位置编码来说,它的灵活性更大,更加体现出了研究人员的“天马行空”。
这样一来,只需要有限个位置编码,就可以表达出任意长度的相对位置(因为进行了截断),不管pK,pV是选择可训练式的还是三角函数式的,都可以达到处理任意长度文本的需求。
而且论文还作了一个假设(后由实验验证),设置一个超参k,当相对距离大于k之后,就认为相对位置量不再随着相对距离的增大而变化,而是统一设为uk
最后不同的Head之间的Relative embedding table是共享的,因此每一层的位置编码参数只有(2k+1)×d×2个。
##########################################################################################
与Sinusoidal Position Embedding比较
正余弦编码仅加在了embedding层,而如上面所论证的,初始的位置编码会在后面被线性变换所干扰。而RPR是在每一层计算attention时都加上了relative position embedding
其“缺点”是超出截断距离的相对位置量不再变化(受限于它的定义),而正余弦编码的好处正是不受限于相对位置的大小
##########################################################################################
2.1 XLNET式 Transformer-XL式
XLNET式位置编码其实源自Transformer-XL的论文《Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context》,只不过因为使用了Transformer-XL架构的XLNET模型并在一定程度上超过了BERT后,Transformer-XL才算广为人知,因此这种位置编码通常也被冠以XLNET之名。

该编码方式中的Ri−j没有像式(6)那样进行截断,而是直接用了Sinusoidal式的生成方案。此外,vj上的位置偏置就直接去掉了,即直接令oi=∑~j~a~i,j~x~j·W~V~。似乎从这个工作开始,后面的相对位置编码都只加到Attention矩阵上去,而不加到vj上去了。
由于RPR的实验表明Value上加的相对位置编码对实验结果影响不大。因此Transfomer_XL中就直接放弃了对Value项的修改,而是专注于Attention Bias项:
2.2 T5式
T5模型出自文章《Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer》,里边用到了一种更简单的相对位置编码。思路依然源自展开式(7),
可以分别理解为“输入-输入”、“输入-位置”、“位置-输入”、“位置-位置”四项注意力的组合。
如果我们认为输入信息与位置信息应该是独立(解耦)的,那么它们就不应该有过多的交互,所以“输入-位置”、“位置-输入”两项Attention可以删掉,而最后一项实际上只是一个只依赖于(i,j)的标量,我们可以直接将它作为参数训练出来
说白了,它仅仅是在Attention矩阵的基础上加一个可训练的偏置项而已,而跟XLNET式一样,在vj上的位置偏置则直接被去掉了。包含同样的思想的还有微软在ICLR 2021的论文《Rethinking Positional Encoding in Language Pre-training》中提出的TUPE位置编码。比较“别致”的是,不同于常规位置编码对将βi,j视为i−j的函数并进行截断的做法,
T5对相对位置进行了一个“分桶”处理,即相对位置是i−j的位置实际上对应的是f(i−j)位置,
具体的映射代码,读者自行看源码就好。这个设计的思路其实也很直观,就是比较邻近的位置(0~7),我们需要比较得精细一些,所以给它们都分配一个独立的位置编码,至于稍远的位置(比如8~11),我们不用区分得太清楚,所以它们可以共用一个位置编码,距离越远,共用的范围就可以越大,直到达到指定范围再clip。
2.3 DeBERTa式
DeBERTa也是微软论文为《DeBERTa: Decoding-enhanced BERT with Disentangled Attention》,最近又小小地火了一把,一是因为它正式中了ICLR 2021,二则是它登上SuperGLUE的榜首,成绩稍微超过了T5。
其实DeBERTa的主要改进也是在位置编码上,同样还是从展开式(7)出发,T5是干脆去掉了第2、3项,只保留第4项并替换为相对位置编码,而DeBERTa则刚刚相反,它扔掉了第4项,保留第2、3项并且替换为相对位置编码(果然,科研就是枚举所有的排列组合看哪个最优):
至于Ri,j的设计也是像式(6)那样进行截断的,没有特别的地方。
不过,DeBERTa比较有意思的地方,是提供了使用相对位置和绝对位置编码的一个新视角,
它指出NLP的大多数任务可能都只需要相对位置信息,但确实有些场景下绝对位置信息更有帮助,于是它将整个模型分为两部分来理解。
以Base版的MLM预训练模型为例,它一共有13层,前11层只是用相对位置编码,这部分称为Encoder,后面2层加入绝对位置信息,这部分它称之为Decoder,还弄了个简称EMD(Enhanced Mask Decoder);至于下游任务的微调截断,则是使用前11层的Encoder加上1层的Decoder来进行。
三 旋转位置编码
3.1 ROPE
RoFormer:https://github.com/ZhuiyiTechnology/roformer
Transformer升级之路:2、博采众长的旋转式位置编码
其中⊗是逐位对应相乘,即Numpy、Tensorflow等计算框架中的∗运算。从这个实现也可以看到,RoPE可以视为是乘性位置编码的变体。
可以看到,RoPE形式上和Sinusoidal位置编码有点相似,只不过Sinusoidal位置编码是加性的,而RoPE可以视为乘性的。
RoPE(Rotary Position Embedding)的出发点就是==“通过绝对位置编码的方式实现相对位置编码”==,或者可以说是实现相对位置编码和绝对位置编码的结合。这样做既有理论上的优雅之处,也有实践上的实用之处,比如它可以拓展到线性Attention中就是主要因为这一点。
3.2 XPOS
XPOS可以看作是对RoPE的略微改进,在RoPE的内积基础上引入了一个指数衰减项,几何上,变换提供向量的旋转。 如果 q 和 k 之间的相对角度较大,则内积为更小。 然而,余弦值并不单调如果旋转角度大于π,这会导致一种不稳定的现象,期望内积随着相对距离的增长。
四 其他位置编码
4.1 CNN式
尽管经典的将CNN用于NLP的工作《Convolutional Sequence to Sequence Learning》往里边加入了位置编码,但我们知道一般的CNN模型尤其是图像中的CNN模型,都是没有另外加位置编码的,那CNN模型究竟是怎么捕捉位置信息的呢?
大家可能会说卷积核的各项异性导致了它能分辨出不同方向的相对位置。不过ICLR 2020的论文《How Much Position Information Do Convolutional Neural Networks Encode?》给出了一个可能让人比较意外的答案:CNN模型的位置信息,是Zero Padding泄漏的!
我们知道,为了使得卷积编码过程中的feature保持一定的大小,我们通常会对输入padding一定的0,而这篇论文显示该操作导致模型有能力识别位置信息。也就是说,卷积核的各向异性固然重要,但是最根本的是zero padding的存在,那么可以想象,实际上提取的是当前位置与padding的边界的相对距离。
不过,这个能力依赖于CNN的局部性,像Attention这种全局的无先验结构并不适用,如果只关心Transformer位置编码方案的读者,这就权当是扩展一下视野吧。
4.2 RMT
2022/07: Recurrent Memory Transformer(RMT): RNN与transformer的结合!
基于 Transformer 的模型展示了它们在多个领域和任务中的有效性。 自注意力允许将来自所有序列元素的信息组合成上下文感知表示。 然而,全局和局部信息必须主要存储在相同的元素方面的表示中。 此外,输入序列的长度受到自注意力的二次计算复杂度的限制。 在这项工作中,我们提出并研究了一种记忆增强的段级循环Transformer(RMT)。 记忆允许存储和处理局部和全局信息,以及在循环的帮助下在长序列的片段之间传递信息。 我们通过向输入或输出序列添加特殊的memory tokens来实现一种记忆机制,而无需更改 Transformer 模型。 然后训练模型以控制记忆操作和序列表示处理。 实验结果表明,对于较小内存大小的语言建模,RMT 的表现与 Transformer-XL 相当,而对于需要较长序列处理的任务则优于它。 我们表明,向 Tr-XL 添加memory tokens能够提高其性能。 这使得 Recurrent Memory Transformer 成为一种很有前途的架构,适用于需要学习长期依赖关系和内存处理通用目的的应用程序,例如算法任务和推理
2023: Scaling Transformer to 1M tokens and beyond with RMT
用RMT来做长度外推
4.2 复数式
复数式位置编码可谓是最特立独行的一种位置编码方案了,它来自ICLR 2020的论文《Encoding word order in complex embeddings》。论文的主要思想是结合复数的性质以及一些基本原理,推导出了它的位置编码形式(Complex Order)为:

代表词j的三组词向量。你没看错,它确实假设每个词有三组跟位置无关的词向量了(当然可以按照某种形式进行参数共享,使得它退化为两组甚至一组),然后跟位置k相关的词向量就按照上述公式运算。
你以为引入多组词向量就是它最特立独行的地方了?并不是!我们看到式(11)还是复数形式,你猜它接下来怎么着?将它实数化?非也,它是将它直接用于复数模型!也就是说,它走的是一条复数模型路线,不仅仅输入的Embedding层是复数的,里边的每一层Transformer都是复数的,它还实现和对比了复数版的Fasttext、LSTM、CNN等模型!这篇文章的一作是Benyou Wang,可以搜到他的相关工作基本上都是围绕着复数模型展开的,可谓复数模型的铁杆粉了~
4.4 ROPE
无偶独有,利用复数的形式,苏神其实也构思了一种比较巧的位置编码,它可以将绝对位置编码与相对位置编码融于一体,分享在此,有兴趣的读者欢迎一起交流研究。
让研究人员绞尽脑汁的Transformer位置编码
Transformer升级之路:2、博采众长的旋转式位置编码
简单起见,我们先假设qm,kn是所在位置分别为m,n的二维行向量,既然是二维,那么我们可以将它当作复数来运算。我们知道,Attention关键之处在于向量的内积,用复数表示为
其中∗是共轭复数,右端的乘法是普通的复数乘法,Re[]表示取结果的实部。上式也就是说:两个二维向量的内积,等于把它们当复数看时,一个复数与另一个复数的共轭的乘积实部。
相当有意思的是,内积只依赖于相对位置m−n!这就巧妙地将绝对位置与相对位置融合在一起了由上述结果可知,对于位置为n的二维实数向量[x,y],我们当它复数来运算,乘以einθ,得到恒等式
这也就是意味着,通过(16)来赋予[x,y]绝对位置信息,那么在Attention运算的时候也等价于相对位置编码。如果是多于二维的向量,可以考虑每两维为一组进行同样的运算,每一组的θ可以不一样。这样一来,我们得到了一种融绝对位置与相对位置于一体的位置编码方案,
从形式上看它有点像乘性的绝对位置编码,通过在q,k中施行该位置编码,那么效果就等价于相对位置编码,
而如果还需要显式的绝对位置信息,则可以同时在v上也施行这种位置编码。
其他
位置embedding与内容embedding的研究
Paper: Constituency Parsing with a Self-Attentive Encoder
我们都知道Transformer模型里的self-attentive结构如下:其中xt = wt+ pt, wt是内容特征, pt是位置特征。然后利用xt分别计算QKVwt和 pt谁更重要?去掉内容特征
为了了解位置特征和内容特征的relative importance,文章做了一个实验
解释:相当于在计算每个词的attentive weight时,只考虑位置信息,而不考虑词语本身的信息。由于本文的任务是做句法分析,因此是在测试只考虑位置信息的attentive weight会对结果有多大的影响。
结果:F1 score只降了0.27将embedding相加改为拼接
接下来,作者猜想直接将两种特征相加,可能会让其中一种信息占主导作用,模型不能很好的找到两种特征重要性的平衡。
事实上,观察注意力权重
其中交叉项【红色部分】可能存在隐患,例如这可能会导致得到这样一个网络:单词 the 总是会特别注意句子的第 5 个位置。这种交叉注意力似乎并没有太大作用,反而会带来过拟合。
因此这个实验里,作者尝试将两种特征由相加改成拼接的方式
结果:比相加的方式还降了0.07个F1 score
结论:事实上,adding 和 concatenation 在高维度上的表现是差不多的,尤其是当结果会立马乘上一个矩阵之后,因为这样会混合里面的信息。拆分位置特征和内容特征
拼接方法效果不行,文章中又尝试了一种新的分解方式,将参数矩阵W WW也进行拆分包括后面的Q ⋅ K Q\cdot KQ⋅K也变成:
对于一个 attention head 来说,拆分后的情况如图所示,可以看成分别对 wt和 pt应用注意力,后续的 feed-forward 层也同样拆分。
结果:F1 score提升了约0.5
结论:表明拆分不同类型的特征确实能得到一个不错的结果。在测试时分别disable位置特征和内容特征
为了分析模型对内容和位置注意力的利用情况,作者又做了个实验,模型训练保持不变,但是在测试阶段,把内容注意力或位置注意力人为置零,即禁用。
结论:位置注意力相当重要,但是内容注意力也有一定帮助,尤其是在最后几层
=============================================================================================
1、绝对位置编码-BERT(学习位置编码)
2、正弦位置编码-Sinusoidal
3、相对位置编码-NEZHA
4、旋转位置编码ROPE
对每一种都进行的讲解,并在代码中详细加了注释!
1、绝对位置编码-BERT
BERT使用的是训练出来的绝对位置编码,这种编码方式简单直接,效果也不错。
这种方法和生成词向量的方法相似,先初始化位置编码,再放到预训练过程中,训练出每个位置的位置向量。
关于该方法的代码如下,用Keras写的,参考苏剑林老师的bert4keras中的代码
from keras.layers import Layer
import keras.backend as K
from keras import initializers
import tensorflow as tf
class PositionEmbedding(Layer):
"""定义可训练的位置Embedding
"""
def __init__(
self,
input_dim,
output_dim,
merge_mode='add',
hierarchical=None,
embeddings_initializer='zeros',
custom_position_ids=False,
**kwargs
):
super(PositionEmbedding, self).__init__(**kwargs)
self.input_dim = input_dim # 输入维度max_position
self.output_dim = output_dim # 输出维度embedding_size,bert中用的是768
self.merge_mode = merge_mode # add模式或者mul模式
self.hierarchical = hierarchical
self.embeddings_initializer = initializers.get(embeddings_initializer)
self.custom_position_ids = custom_position_ids
def build(self, input_shape):
super(PositionEmbedding, self).build(input_shape)
self.embeddings = self.add_weight(
name='embeddings',
shape=(self.input_dim, self.output_dim),
initializer=self.embeddings_initializer
) # 初始化待训练的位置编码权重
def call(self, inputs):
"""如果custom_position_ids,那么第二个输入为自定义的位置id
"""
input_shape = K.shape(inputs)
batch_size, seq_len = input_shape[0], input_shape[1]
# 自己输入位置编码及其位置id
if self.custom_position_ids:
inputs, position_ids = inputs
if K.dtype(position_ids) != 'int32':
position_ids = K.cast(position_ids, 'int32')
else:
# 得到位置编码id 加了[None]变成两维的 [[0,1,2,...,seq_len]]
position_ids = K.arange(0, seq_len, dtype='int32')[None]
if self.hierarchical:
alpha = 0.4 if self.hierarchical is True else self.hierarchical
embeddings = self.embeddings - alpha * self.embeddings[:1]
embeddings = embeddings / (1 - alpha)
embeddings_x = K.gather(embeddings, position_ids // self.input_dim)
embeddings_y = K.gather(embeddings, position_ids % self.input_dim)
pos_embeddings = alpha * embeddings_x + (1 - alpha) * embeddings_y
else:
# 如果是自己输入位置编码,就用位置id读取相应的位置编码
if self.custom_position_ids:
pos_embeddings = K.gather(self.embeddings, position_ids)
else:
# 直接拿初始化的位置编码权重
pos_embeddings = self.embeddings[None, :seq_len]
# add模式直接把原有特征和位置编码相加即可
if self.merge_mode == 'add':
return inputs + pos_embeddings
# mul模式是把原有特征和位置编码对应相乘
elif self.merge_mode == 'mul':
return inputs * pos_embeddings
else:
if not self.custom_position_ids:
pos_embeddings = K.tile(pos_embeddings, [batch_size, 1, 1])
# 如果不属于上述两种模式,则用concat的形式
return K.concatenate([inputs, pos_embeddings])
def compute_output_shape(self, input_shape):
if self.custom_position_ids:
input_shape = input_shape[0]
if self.merge_mode in ['add', 'mul']:
return input_shape
else:
return input_shape[:2] + (input_shape[2] + self.output_dim,)
def get_config(self):
config = {
'input_dim': self.input_dim,
'output_dim': self.output_dim,
'merge_mode': self.merge_mode,
'hierarchical': self.hierarchical,
'embeddings_initializer':
initializers.serialize(self.embeddings_initializer),
'custom_position_ids': self.custom_position_ids,
}
base_config = super(PositionEmbedding, self).get_config()
return dict(list(base_config.items()) + list(config.items()))
2、正弦位置编码
使用绝对位置编码,不同位置对应的位置编码固然不同,但是位置1和位置2的距离,比位置2和位置5的距离更近;而位置1和位置2的距离,和位置3和位置4的距离都只相差1;
而在BERT中通过学习位置编码的方式,位置之间是没有约束关系的,我们能做的就只是期待他能够学到并理解这些位置的相对关系。
所以可以用以下的方式来表达约束位置编码:正弦位置编码和相对位置编码
正弦这一类的参数式位置编码中涉及两个概念:一个是距离,另一个是维度
所以在涉及计算公式的时候,每个字之间按顺序给他id,用来代表着距离,就是pos这个词参数;另一个是维度,同一个字中不同维度的特征信息,可以用sin和cos的方式计算。
这种方法是使用不同频率的正弦、余弦函数生成,然后再和对应位置的词向量相加
其中pos表示对应输入的位置,表示的是seq_len这个维度上;i表示的是维度,表示的是768个。
奇偶相配合
class SinusoidalPositionEmbedding(Layer):
"""定义Sin-Cos位置Embedding
"""
def __init__(
self, output_dim, merge_mode='add', custom_position_ids=False, **kwargs
):
super(SinusoidalPositionEmbedding, self).__init__(**kwargs)
self.output_dim = output_dim
self.merge_mode = merge_mode
self.custom_position_ids = custom_position_ids
def call(self, inputs):
"""如果custom_position_ids,那么第二个输入为自定义的位置id
"""
input_shape = K.shape(inputs)
batch_size, seq_len = input_shape[0], input_shape[1]
if self.custom_position_ids:
inputs, position_ids = inputs
else:
# 得到位置编码id 加了[None]变成两维的 [[0,1,2,...,seq_len]]
position_ids = K.arange(0, seq_len, dtype=K.floatx())[None]
# 根据公式开始计算
# 取一半的,方便2i的计算
indices = K.arange(0, self.output_dim // 2, dtype=K.floatx())
# 对前一个参数x,取后一个参数y的平方,x^y,即10000^(2i/dim)
indices = K.pow(10000.0, -2 * indices / self.output_dim)
# shape=(btz, seq_len, dim)
pos_embeddings = tf.einsum('bn,d->bnd', position_ids, indices)
pos_embeddings = K.concatenate([
K.sin(pos_embeddings)[..., None],
K.cos(pos_embeddings)[..., None]
])
# [...,None]会在最后一维增加一维,把每个值用[]包起来
# 比如a = K.arange(0, 10) 本来输出的是:[0 1 2 3 4 5 6 7 8 9];a = K.arange(0, 10)[..., None]变成了[[0] [1] [2] [3] [4] [5] [6] [7] [8] [9]]
# 同K.expand_dim(pos_embeddings, -1)的效果
# 重新reshape成shape=(btz, seq_len, dim)
pos_embeddings = K.reshape(
pos_embeddings, (-1, seq_len, self.output_dim)
)
if self.merge_mode == 'add':
return inputs + pos_embeddings
elif self.merge_mode == 'mul':
return inputs * pos_embeddings
else:
if not self.custom_position_ids:
pos_embeddings = K.tile(pos_embeddings, [batch_size, 1, 1])
return K.concatenate([inputs, pos_embeddings])
def compute_output_shape(self, input_shape):
if self.custom_position_ids:
input_shape = input_shape[0]
if self.merge_mode in ['add', 'mul']:
return input_shape
else:
return input_shape[:2] + (input_shape[2] + self.output_dim,)
def get_config(self):
config = {
'output_dim': self.output_dim,
'merge_mode': self.merge_mode,
'custom_position_ids': self.custom_position_ids,
}
base_config = super(SinusoidalPositionEmbedding, self).get_config()
return dict(list(base_config.items()) + list(config.items()))
3、相对位置编码
相对位置编码的代表作就是NEZHA
参数式训练会受到句子长度的影响,bert起初训练的句子最长为512,如果只训练到128长度的句子,那在128—512之间的位置参数就无法获得,所以必须要训练更长的预料来确定这一部分的参数
在NAZHA中,距离和维度都是用正弦函数导出来的,并且在模型训练期间也是固定的。
class RelativePositionEmbedding(Layer):
"""相对位置编码
来自论文:https://arxiv.org/abs/1803.02155
"""
def __init__(
self, input_dim, output_dim, embeddings_initializer='zeros', **kwargs
):
super(RelativePositionEmbedding, self).__init__(**kwargs)
self.input_dim = input_dim # 129
self.output_dim = output_dim # attention_head_size每一头的维度 768/12=64
self.embeddings_initializer = initializers.get(embeddings_initializer)
def build(self, input_shape):
super(RelativePositionEmbedding, self).build(input_shape)
# 初始化待训练的位置编码权重
self.embeddings = self.add_weight(
name='embeddings',
shape=(self.input_dim, self.output_dim),
initializer=self.embeddings_initializer,
)
def call(self, inputs):
# 根据位置id获取位置编码 每一种的不一样,比如位置id=1的和位置id=-1的就不一样,读取进来,
pos_ids = self.compute_position_ids(inputs)
return K.gather(self.embeddings, pos_ids) # 输出的时候需要是(btz,seq_len,dim)
def compute_position_ids(self, inputs):
q, v = inputs # [x, x]
# 计算位置差
# 一维[0,1,...,q_seq_len]
q_idxs = K.arange(0, K.shape(q)[1], dtype='int32')
# [[0] [1] [2] [3] ... [q_seq_len]]
q_idxs = K.expand_dims(q_idxs, 1)
v_idxs = K.arange(0, K.shape(v)[1], dtype='int32')
# [[0,1,...,v_seq_len]]
v_idxs = K.expand_dims(v_idxs, 0)
pos_ids = v_idxs - q_idxs
'''以q_seq_len=v_seq_len=9为例:
[[ 0 1 2 3 4 5 6 7 8 9]
[-1 0 1 2 3 4 5 6 7 8]
[-2 -1 0 1 2 3 4 5 6 7]
[-3 -2 -1 0 1 2 3 4 5 6]
[-4 -3 -2 -1 0 1 2 3 4 5]
[-5 -4 -3 -2 -1 0 1 2 3 4]
[-6 -5 -4 -3 -2 -1 0 1 2 3]
[-7 -6 -5 -4 -3 -2 -1 0 1 2]
[-8 -7 -6 -5 -4 -3 -2 -1 0 1]
[-9 -8 -7 -6 -5 -4 -3 -2 -1 0]]
相对位置编码就比较简单的用这种差几位数来表示相对位置
'''
# 后处理操作
max_position = (self.input_dim - 1) // 2
'''
K.clip:逐元素clip,将pos_ids中超出(-max_position, max_position)范围的数强制变为边界值
1、作者假设精确的相对位置编码在超出了一定距离之后是没有必要的
2、截断最大距离使得模型的泛化效果好,可以更好的generalize到没有在训练阶段出现过的序列长度上
比如上面的例子中,截到(-4,4)之间为:
[[ 0 1 2 3 4 4 4 4 4 4]
[-1 0 1 2 3 4 4 4 4 4]
[-2 -1 0 1 2 3 4 4 4 4]
[-3 -2 -1 0 1 2 3 4 4 4]
[-4 -3 -2 -1 0 1 2 3 4 4]
[-4 -4 -3 -2 -1 0 1 2 3 4]
[-4 -4 -4 -3 -2 -1 0 1 2 3]
[-4 -4 -4 -4 -3 -2 -1 0 1 2]
[-4 -4 -4 -4 -4 -3 -2 -1 0 1]
[-4 -4 -4 -4 -4 -4 -3 -2 -1 0]]
'''
pos_ids = K.clip(pos_ids, -max_position,
max_position)
pos_ids = pos_ids + max_position # shape=(q_seq_lenv, v_seq_len)
return pos_ids
def compute_output_shape(self, input_shape):
return (None, None, self.output_dim)
def compute_mask(self, inputs, mask):
return mask[0]
def get_config(self):
config = {
'input_dim': self.input_dim,
'output_dim': self.output_dim,
'embeddings_initializer':
initializers.serialize(self.embeddings_initializer),
}
base_config = super(RelativePositionEmbedding, self).get_config()
return dict(list(base_config.items()) + list(config.items()))
4、旋转位置编码:
旋转位置编码其实就是在attention计算q*k中用 Rij替代两个位置向量:

苏神最近更新了位置编码的两种分类,更加清、晰直观,可参考
让研究人员绞尽脑汁的Transformer位置编码 - 科学空间|Scientific Spaces
来源:
https://zhuanlan.zhihu.com/p/334355417