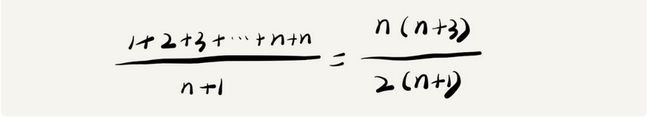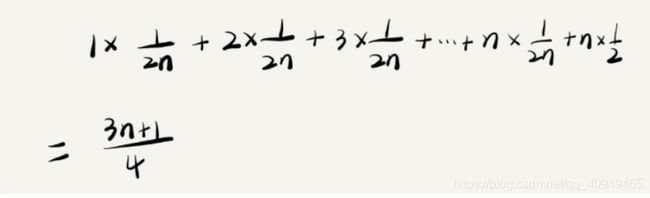数据结构与算法 --时间复杂度分析(二)
数据结构和算法解决代码的“快”“省”,而时间、空间复杂度做为数据结构和算法的精髓,很直观说明了代码”多快“”多省“
一、为什么需要复杂度分析?
代码跑一遍,通过统计,监控,得到的算法执行的时间占用的内存大小叫事后统计法
事后统计法具有局限性:
- 测试结果非常依赖测试环境
- 测试结果受数据规模的影响很大
所以,我们需要一个不用具体的测试数据来测试,就可以粗略地估计算法的执行效率的方法
二、大O复杂度表示法
T(n) = O(f(n))
n表示数据规模的大小,f(n)表示每行代码的执行次数之和
所有代码的执行时间 T(n) 与每行代码的执行次数 n 成正比
大 O 时间复杂度实际上并不具体表示代码真正的执行时间,而是代码执行时间随数据规模增长的变化趋势,所以叫渐进时间复杂度,简称时间复杂度
(当 n 很大时,你可以把它想象成 10000、100000。而公式中的低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略。我们只需要记录一个最大量级就可以了。
计算时间复杂度的方法:
1.只关注循环执行次数最多的一段代码
2. 加法法则:总复杂度等于量级最大的那段代码的复杂度
如果 T1(n)=O(f(n)),T2(n)=O(g(n));那么T(n)=T1(n)+T2(n)=max(O(f(n)),O(g(n))=O(max(f(n), g(n)))
3.乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
T1(n)=O(f(n)),T2(n)=O(g(n));那么T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n)).
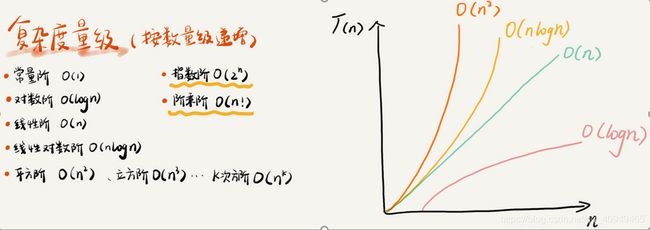
三、几种常见的复杂度分析
多项式阶:随着数据规模的增长,算法的执行时间和空间占用,按照多项式的比例增长。包括,
O(1)(常数阶)、O(logn)(对数阶)、O(n)(线性阶)、O(nlogn)(线性对数阶)、O(n^2)(平方阶)、O(n^3)(立方阶)
非多项式阶:随着数据规模的增长,算法的执行时间和空间占用暴增,这类算法性能极差。包括,
O(2^n)(指数阶)、O(n!)(阶乘阶
几种常见的多项式时间复杂度 :
1、O(1)
O(1)只是常量级时间复杂度的一种表示方法,并不是指只执行了一行代码。比如这段代码,即便三行,时间复杂度也是O(1),而不是O(3)
int i = 8;
int j = 6;
int sum = i + j;
只要代码的执行时间不随数据规模的n的增大而增大,那么代码的时间复杂度就为O(1).
一般只要算法中不存在循环,递归,无论代码上千行都是O(1)
2、O(logn)、O(nlogn)
i=1;
while (i <= n) {
i = i * 2;
}
我们只需要知道x的值,就知道执行多少次了 ,也就是求2的x次幂=n,x=log2n就是时间复杂度
i=1;
while (i <= n) {
i = i * 3;
}
显然就是O(log3n)
所有对数的时间复杂度都为logn 因为,log2n=log3n/log32=log23*log3n
根据乘法法则,如果一段代码的时间复杂度为O(logn),循环执行n遍,时间复杂度就是O(nlogn)。O(nlogn)也是非常常见的时间复杂度,如归并排序,快速排序。
3. O(m+n)、O(m*n)
这是两个数据规模的情况,我们无法事先评估哪个量级大,所以加法法则就不适用了,只能是O(m+n)。
但是乘法法则继续有效:T1(m)*T2(n) = O(f(m) * f(n))
四、空间复杂度
时间复杂度全称渐进时间复杂度,表示算法的执行时间随问题规模增大的变化趋势
类比,空间复杂度全称就是渐进空间复杂度,表示算法的存储空间与数据规模之间的增长关系
五:复杂度分析的4个概念
1.最坏情况时间复杂度:代码在最理想情况下执行的时间复杂度。
2.最好情况时间复杂度:代码在最坏情况下执行的时间复杂度。
3.平均时间复杂度:用代码在所有情况下执行的次数的加权平均值表示。
4.均摊时间复杂度:在代码执行的所有复杂度情况中绝大部分是低级别的复杂度,个别情况是高级别复杂度且发生具有时序关系时,可以将个别高级别复杂度均摊到低级别复杂度上。基本上均摊结果就等于低级别复杂度
在能够应用均摊时间复杂度分析的场合,一般均摊时间复杂度就等于最好情况时间复杂度
-
最好、最坏时间复杂度
// n 表示数组 array 的长度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) pos = i;
}
return pos;
}
这段代码是在一个无序数组里查找变量x的位置,没有找到返回-1。时间复杂度为O(n)
由于我们查找一个数据,并不要每次都遍历数组,有可能中途找到,提前结束。我们来优化一下上面代码
// n 表示数组 array 的长度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) {
pos = i;
break;
}
}
return pos;
}
当第一个元素就是我们要找的,那么剩余n-1个元素就不需要遍历了,那么最好时间复杂度为O(1)。当数组中不存在x,那么就需要遍历整个数组,那么最坏时间复杂度就是O(n)。
-
平均情况时间复杂度
因为最好最好坏时间复杂度都是极端情况,发生几率小,为了更好的表示平均情况时间复杂度,我们引入另一个概念:平均情况时间复杂度,简称平均时间复杂度
要查找变量x在数组中有n+1种情况,在数组0~n-1的位置和不在数组中。我们把每种情况下,查找需要遍历的元素个数累加起来,然后除以n+1,就得到需要遍历的元素个数的平均值
因此平均时间复杂度就是O(n)
由于n+1种情况出现的概率并不是一样的。为了方便理解,我们假设在数组中与不在数组中的概率都为1/2。要查找的数据出现在0~n-1这n个位置的概率为1/n。根据概率乘法法则,要查找的数据出现在0~n-1中任意位置的概率是1/2n。
这个值就是概率论中的加权平均值,也叫做期望。所以这段代码的加权平均时间复杂度仍然是O(n)
-
均摊时间复杂度
// 全局变量,大小为 10 的数组 array,长度 len,下标 i。
int array[] = new int[10];
int len = 10;
int i = 0;
// 往数组中添加一个元素
void add(int element) {
if (i >= len) { // 数组空间不够了
// 重新申请一个 2 倍大小的数组空间
int new_array[] = new int[len*2];
// 把原来 array 数组中的数据依次 copy 到 new_array
for (int j = 0; j < len; ++j) {
new_array[j] = array[j];
}
// new_array 复制给 array,array 现在大小就是 2 倍 len 了
array = new_array;
len = 2 * len;
}
// 将 element 放到下标为 i 的位置,下标 i 加一
array[i] = element;
++i;
}
当i < len时, 即 i = 0,1,2,...,n-1的时候,for循环不走,所以这n次的时间复杂度都是O(1);
当i >= len时, 即 i = n的时候,for循环进行数组的copy,所以只有这1次的时间复杂度是O(n);
由此可知:
该算法的最好情况时间复杂度(best case time complexity)为O(1)
最坏情况时间复杂度(worst case time complexity)为O(n)
平均情况时间复杂度(average case time complexity)
第一种计算方式: (1+1+...+1+n)/(n+1) = 2n/(n+1) 【注: 式子中1+1+...+1中有n个1】,所以平均复杂度为O(1);
第二种计算方式(加权平均法,又称期望): 1*(1/n+1)+1*(1/n+1)+...+1*(1/n+1)+n*(1/(n+1))=1,所以加权平均时间复杂度为O(1);
第三种计算方式(均摊时间复杂度): 前n个操作复杂度都是O(1),第n+1次操作的复杂度是O(n),所以把最后一次的复杂度分摊到前n次上,那么均摊下来每次操作的复杂度为O(1)
六:题目
1.【2011年计算机联考真题】
设n是描述问题规模的非负整数,下面程序片段的时间复杂度是()。
x=2;
while(xA. O(log2n) B. O(n) C. O(nlog2n) D. O(n2)
A
在程序中,执行频率最高的语句为“x=2*x”。设该语句共执行了 t次,则2t+1=n/2,故t=log2(n/2)-1=log2n-2,得 T(n)=O(log2n)。
2.【2012年计算机联考真题】
求整数n (n>=0)阶乘的算法如下,其时间复杂度是( )。
int fact(int n){
if (n<=l) return 1;
return n*fact(n-1);
}A. O(log2n) B. O(n) C. O(nlog2n) D. O(n2)
B
本题是求阶乘n!的递归代码,即n*(n-1)*...*1共执行n次乘法操作,故T(n)=O(n)。