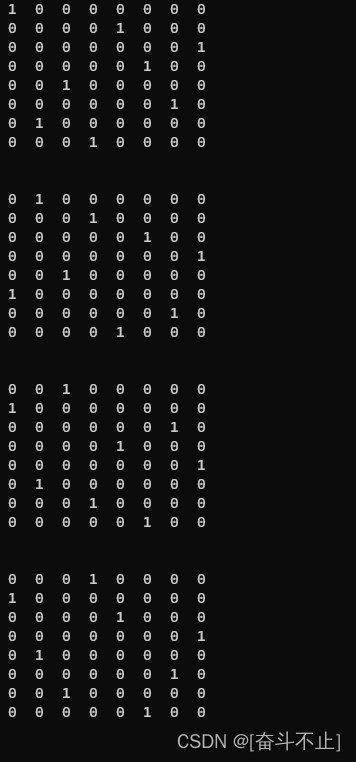
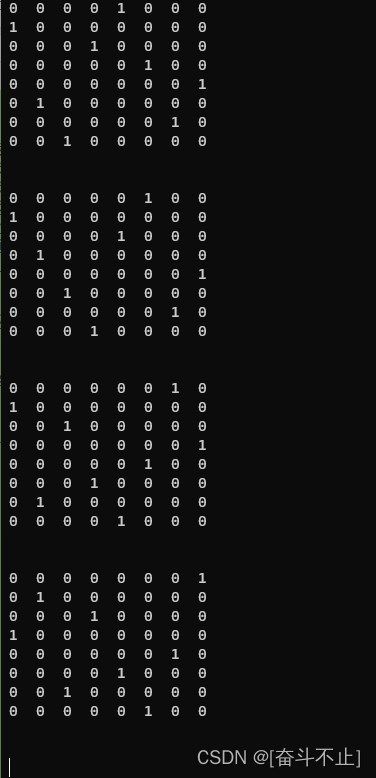
N 皇后问题

N 皇后问题研究的是如何将 N 个皇后放置在 N x N 的棋牌上，并且使皇后彼此之间不能相互攻击。

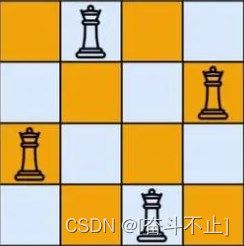
国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子

解决思路是：剪枝 + 回溯方法 解决问题

(1).使用二维数组创建棋牌格子 grid
(2).将数组中每个元素赋值 为 0
(3).在某一行，某一列位置，如果格子数值为 0 ，则格子可以放置皇后
(4).在一个位置放置一个皇后，记录皇后位置，并将其所在同一行、同一列、同一斜线上的格子数值 +1
(5).回溯，将原本放置皇后的位置，取消放置，删除记录，将其同一行、同一列、同一斜线上的格子数值 -1

分析：因为每一行只能放置，且必须放置一个皇后
A.使用递归函数来实现，按照每次递归一行棋牌来考虑，每一行 (M行) 只要有一个位置满足如上 (3) 条件，就可以放置皇后到该位置，我们记录放置皇后的位置，然后执行 如上 (4)，
B. 然后递归到下一行（M+1行），当我们递归到某行(S行)发现没有位置可以放置皇后了，我们就要回溯 执行如上 (5)，返回到上一行(S-1 行)没有放置皇后的时候，然后在上一行(S-1 行)换一个可以放置皇后的位置，来放置皇后
经过如上的递归一直到N行都放置了皇后，就完成所有皇后的放置了

代码如下

public class EightQueensProblem
{
    private const int N = 8;
    private int[,] grid = new int[N, N];

    private Dictionary<int, int> dic = new Dictionary<int, int>();
    private List<int[]> dirList = new List<int[]>()
    {
        new int[] { -1,  0 },
        new int[] {  1,  0 },
        new int[] {  0, -1 },
        new int[] {  0,  1 },
        new int[] { -1, -1 },
        new int[] { -1,  1 },
        new int[] {  1, -1 },
        new int[] {  1,  1 },
    };

    public EightQueensProblem()
    {
        for (int col = 0; col < N; col++)
        {
            dic.Clear();
            // 创建棋牌格子
            CreateGrid();

            // 初始在第 1 行，不同列放置一个皇后
            SetQueens(0, col, true);
            // 因为第 1 行，已经放置了皇后了，所以从第 1 行开始计算
            int row = 1;
            Calculate(row);
            // 重新创建一个空的棋牌格子
            CreateGrid();
            // 将皇后放置结果填写进去
            foreach (var kv in dic)
            {
                int r = kv.Key;
                int c = kv.Value;
                grid[r, c] = 1;
            }
            // 将棋牌打印出来
            Print();
        }
    }

    /// 

    /// 递归 加 回溯方法 计算每一行可以放置 Queens 的位置
    /// 
    /// 
    private void Calculate(int row)
    {
        // 如果已经放置 N 个了，说明已经放置完成了
        if (dic.Count >= N)
        {
            return;
        }

        for (int col = 0;  col < N; ++col)
        {
            if (grid[row, col] == 0 && dic.Count < N)
            {
                // 记录放置 Queens 的位置
                SetQueens(row, col, true);

                // 计算下一行
                Calculate(row + 1);

                // 如果已经放置 N 个了，说明已经放置完成了
                if (dic.Count < N)
                {
                    // 取消放置 Queens 的位置
                    SetQueens(row, col, false);
                }
            }
        }
    }

    /// 

    /// 打印棋牌格子
    /// 
    private void Print()
    {
        for (int row = 0; row < N; ++row)
        {
            string msg = string.Empty;
            for (int col = 0; col < N; ++col)
            {
                int value = grid[row, col];
                msg += string.Format("{0}  ", value);
            }
            Console.WriteLine(msg);
        }
        Console.WriteLine();
        Console.WriteLine();
    }

    /// 

    /// 创建棋牌格子
    /// 
    private void CreateGrid()
    {
        for (int row = 0; row < N; ++row)
        {
            for (int col = 0; col < N; ++col)
            {
                grid[row, col] = 0;
            }
        }
    }

    /// 

    /// row、col 放置 Queens 令 所在行、列、斜向 都 加 1
    /// row、col 取消 Queens 令 所在行、列、斜向 都 减 1
    /// 
    /// 
    /// 
    /// true 放置，false 取消
    private void SetQueens(int row, int col, bool add)
    {
        if (dic.Count >= N)
        {
            return;
        }

        if (add)
        {
            dic[row] = col;
        }
        else
        {
            dic.Remove(row);
        }

        int offset = (add ? 1 : -1);
        grid[row, col] += offset;
        foreach (var dir in dirList)
        {
            int tempRow = row;
            int tempCol = col;
            while (true)
            {
                tempRow += dir[0];
                tempCol += dir[1];
                if (tempRow < 0 || tempRow >= N || tempCol < 0 || tempCol >= N)
                {
                    break;
                }
                grid[tempRow, tempCol] += offset;
                if (add)
                {
                    CheckSet(tempRow, tempCol);
                }
            }
        }
    }

    // 放置皇后时，检测同一行、同一列、同一斜线上是否已经放置了皇后
    private void CheckSet(int row, int col)
    {
        int c = 0;
        if (!dic.TryGetValue(row, out c))
        {
            return;
        }
        if (c == col)
        {
            Console.WriteLine("Check Error:" + row + "   " + col);
        }
    }
}

运行结果如下