机器学习笔记--支持向量机

1、支持向量机概述

1.1 基本概念

支持向量机（Support Vector Machine,SVM ） 是一类按监督学习方式对数据进行二元分类 的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面 。

1.2 硬间隔、软间隔和非线性 SVM

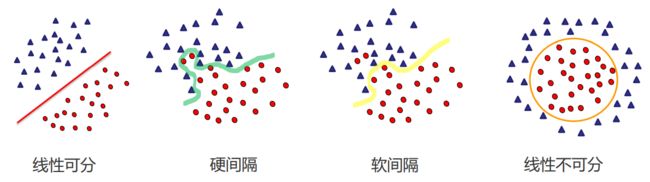
硬间隔指的就是完全分类准确，不能存在分类错误的情况。软间隔，就是允许一定量的样本分类错误。

1.3 算法思想

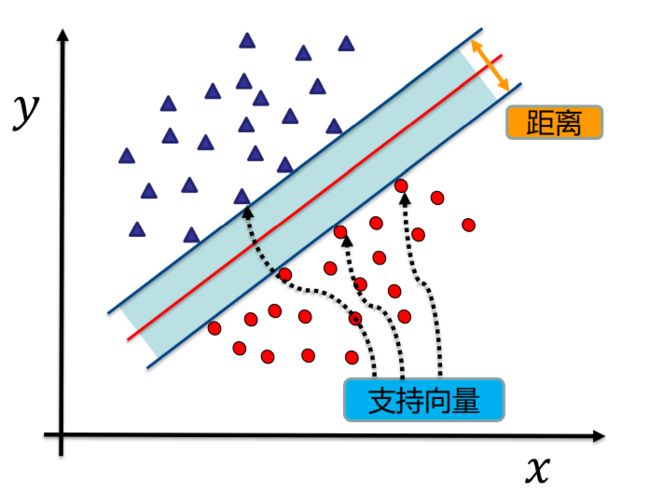
找到集合边缘上的若干数据（称为支持向量（Support Vector）），用这些点找出一个平面（称为决策面），使得支持向量到该平面的距离最大。

2、支持向量机求解

2.1 基础知识

（1）任意超平面均可用下面的线性方程来表示：
$$w^{T}x+b=0$$
（2）二维空间点 (, )到直线 + + =0 的距离公式是：
$$\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}$$
推广到 n 维空间，点到超平面的距离为：
∣ w T x + b ∣ ∥ w ∥ \frac{\left|w^{T} x+b\right|}{\|w\|} ∥w∥ ​wTx+b ​​
其中，$\Vert w\Vert =\sqrt{w_1^2+\cdots w_n^2}$

2.2 计算求解

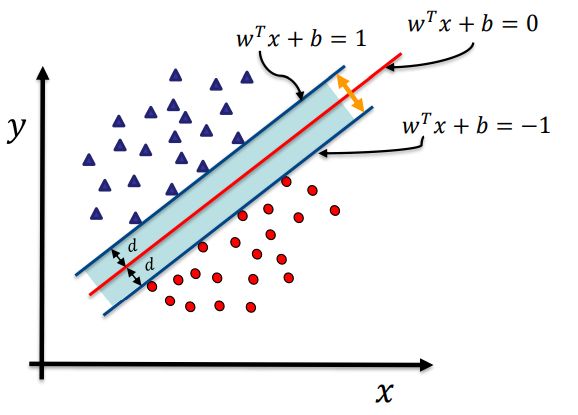
（1）如上图，根据定义我们可以知道，支持向量到超平面$w^{T}x+b=0$ 的距离为 d ，则其他点到超平面的距离均大于 d 。

对于样本点$（x_i,y_i）$,若$y_1=+1$ ,则$w^{T}x+b>d$；若$y_1=-1$ ,则$w^{T}x+b<-d$。于是有

$$\{\begin{array}{cc}\frac{w^{T}x+b}{\Vert w\Vert }\ge d& y=+1\\ & \\ \frac{w^{T}x+b}{\Vert w\Vert }\le -d& y=-1\end{array}$$

暂且令 d=1（之所以令它等于 1，是为了方便推导和优化
，且这样做对目标函数的优化没有影响，可以缩放变换），则上式可合并为

$$y\left(w^{T}x+b\right)\ge 1$$

两个边界平面的间隔为：
$$\gamma =\frac{2}{\Vert \mathbf{w}\Vert }$$
欲找到最大间隔来划分超平面，也就是要找到满足约束的 $\omega$ 和 b ,使 $\gamma$ 最大。即

$$\begin{array}{rl}& \underset{\mathbf{w},b}{\max }\frac{2}{\Vert \mathbf{w}\Vert }\\ & \\ & \text{ s.t. }{y}_i\left({\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_i+b\right)⩾1,i=1,2,\dots ,m\end{array}$$

这等价于最小化$\Vert \mathbf{w}{\Vert }^2$,则上式改写为
$$\begin{array}{rl}& \underset{\mathbf{w},b}{\min }\frac{1}{2}\Vert \mathbf{w}{\Vert }^2\\ & \\ & \text{ s.t. }{y}_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1,i=1,2,\dots ,m\end{array}$$

（2）用拉格朗日乘子法和KKT条件求解最优值：

该问题的拉格朗日函数可写为：

$$L(w,b,\alpha )=\frac{1}{2}\Vert w{\Vert }^2+\sum _{i=1}^m{\alpha }_i\left(-y_i\left(w^T{x}_i+b\right)+1\right)$$
求导

$$\{\begin{array}{c}\frac{\partial }{\partial w}L(w,b,\alpha )=w-{\sum }_{i=1}^m{\alpha }_i{y}_i{x}_i=0\\ \\ \frac{\partial }{\partial b}L(w,b,\alpha )={\sum }_{i=1}^m{\alpha }_i{y}_i=0\end{array}$$
解得
$$\{\begin{array}{c}w={\sum }_{i=1}^m{\alpha }_i{y}_i{x}_i\\ \\ {\sum }_{i=1}^m{\alpha }_i{y}_i=0\end{array}$$

再代入$L(w,b,\alpha )$，得

$$\begin{array}{c}\underset{w,b}{\min }L(w,b,\alpha )=\frac{1}{2}\Vert w{\Vert }^2+\sum _{i=1}{\alpha }_i\left(-y_i\left(w^T{x}_i+b\right)+1\right)\\ =\frac{1}{2}{w}^{T}w-\sum _{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i-b\sum _{i=1}^m{\alpha }_i{y}_i+\sum _{i=1}^m{\alpha }_i\\ =\frac{1}{2}{w}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i-\sum _{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i+\sum _{i=1}^m{\alpha }_i\\ =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i\\ =\sum _{i=1}^m{\alpha }_i-\sum _{i,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)\end{array}$$
$$\begin{array}{ll}\text{ s.t. }& {\sum }_{i=1}^m{\alpha }_i{y}_i=0,\\ & {\alpha }_i⩾0,i=1,2,\dots ,m\end{array}$$

用 SMO 算法求解出 ${\alpha }_i$，最终得到超平面
$$\begin{array}{rl}f(\mathbf{x})& ={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_i^{\mathrm{T}}\mathbf{x}+b\end{array}$$

3、线性支持向量机（软间隔支持向量机）与松弛变量

在前面的讨论中，我们假设训练样本在样本空间或者特征空间中是线性可分的，但在现实任务中往往很难确定合适的核函数使训练集在特征空间中线性可分。

线性不可分意味着某些样本点$（x_i,y_i）$不能满足间隔大于等于1的条件，样本点落在超平面与边界之间。为解决这一问题，可以对每个样本点引入一个松弛变量${\xi }_i\ge 0$，使得间隔加上松弛变量大于等于1，这样约束条件变为：

$$y_i\left(w^T{x}_i+b\right)+{\xi }_i\ge 1$$
也即

$$y_i\left(w^T{x}_i+b\right)\ge 1-{\xi }_i$$
同时，对于每一个松弛变量${\xi }_i\ge 0$，支付一个代价 ${\xi }_i\ge 0$，目标函数变为

$$\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^m{\xi }_i$$

其中 C>0 为惩罚参数，C 值大时对误分类的惩罚增大，C值小时对误分类的惩罚减小，上式包含两层含义：使$\frac{1}{2}\Vert w{\Vert }^2$尽量小即间隔尽量大，同时使误分类点的个数尽量小， C 是调和两者的系数。

跟线性可分求解的思路一致，同样这里先用拉格朗日乘子法得到拉格朗日函数，再求其对偶问题。

可以这样理解

• C 较大时，相当于 较小，可能会导致过拟合，高方差。
• C 较小时，相当于 较大，可能会导致低拟合，高偏差。

4、线性不可分支持向量机

4.1 核函数

在低维空间计算获得高维空间的计算结果，满足高维，才能在高维下线性可分。

我们需要引入一个新的概念：核函数。它可以将样本从原始空间映射到一个更高维的特质空间中，使得样本在新的空间中线性可分。

这样我们就可以使用原来的推导来进行计算，只是所有的推导是在新的空间，而不是在原来的空间中进行，即用核函数来替换当中的内积。

用$\varphi (x)$表示将 x 映射后的特征向量，于是在特征空间中，划分超平面所对应的的模型可表示为：

$$f(x)=w^T\varphi (x)+b$$
于是有最小化函数

$$\underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2,\text{ s.t. }{y}_i\left(w^T\varphi \left(x_i\right)+b\right)\ge 1(i=1,2,\dots ,m)$$
其对偶问题为

$$\begin{array}{rl}& \underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi {\left(x_i\right)}^T\varphi \left(x_j\right)\\ & \text{ s.t. }\sum _{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i\ge 0,i=1,2,\dots ,m\end{array}$$
这里会涉及到计算 $\varphi {\left(x_i\right)}^T\varphi \left(x_j\right)$，即样本$x_i$ 和 $x_j$映射到特征空间后的内积，直接计算是十分困难的，于是有核函数

$$\kappa \left(x_i,x_j\right)=<\varphi \left(x_i\right),\varphi \left(x_j\right)>=\varphi {\left(x_i\right)}^T\varphi \left(x_j\right)$$
则上式可写为
$$\begin{array}{rl}& \underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa \left(x_i,x_j\right)\\ & \text{ s.t. }\sum _{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i\ge 0,i=1,2,\dots ,m\end{array}$$
求解后得到
$$\begin{array}{rl}f(x)& =w^T\varphi (x)+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\varphi {\left(x_i\right)}^T\varphi \left(x_j\right)+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\kappa \left(x_i,x_j\right)+b\end{array}$$

常用的核函数有：

• 线性核函数
  $$K\left(x_i,x_j\right)=x_i^T{x}_j$$
  即该向量机不适用核函数
• 多项式核函数

$$K\left(x_i,x_j\right)={\left(x_i^T{x}_j\right)}^d$$

• 高斯核函数

$$K\left(x_i,x_j\right)=\exp \left(-\frac{\Vert x_i-x_j\Vert }{2{\delta }^2}\right)$$

4.2 SVM 使用准则

（1）SVM 的超参数

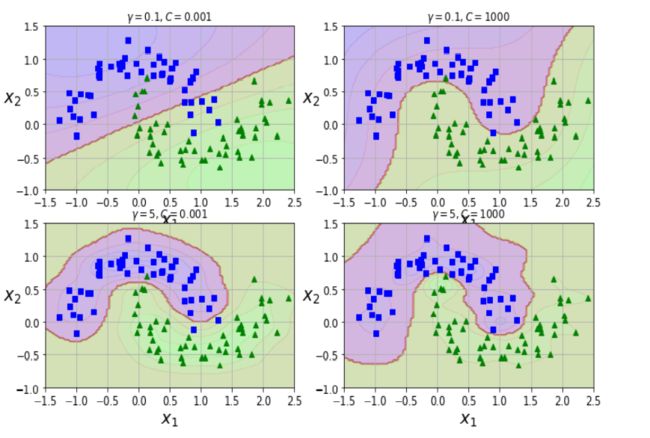
• 越大，支持向量越少，值越小，支持向量越多。

• $C=1/\lambda$较大时，相当于较小，可能会导致过拟合，高方差；

• $C=1/\lambda$较小时，相当于较大，可能会导致低拟合，高偏差；

• 较大时，可能会导致低方差，高偏差；

• 较小时，可能会导致低偏差，高方差。

（2）SVM 使用准则

n为特征数，m为训练样本数。

• 如果相较于 m 而言，n 要大许多，即训练集数据量不够支持我们训练一个复杂的非线性模型，我们选用逻辑回归模型或者不带核函数的支持向量机。

• 如果 n 较小，而且 m 大小中等，例如 n 在 1-1000 之间，而 m 在 10-10000 之间，使用高斯核函数的支持向量机。

• 如果 n 较小，而 m 较大，例如 n 在 1-1000 之间，而 m 大于 50000，则使用支持向量机会非常慢，解决方案是创造、增加更多的特征，然后使用逻辑回归或不带核函数的支持向量机。