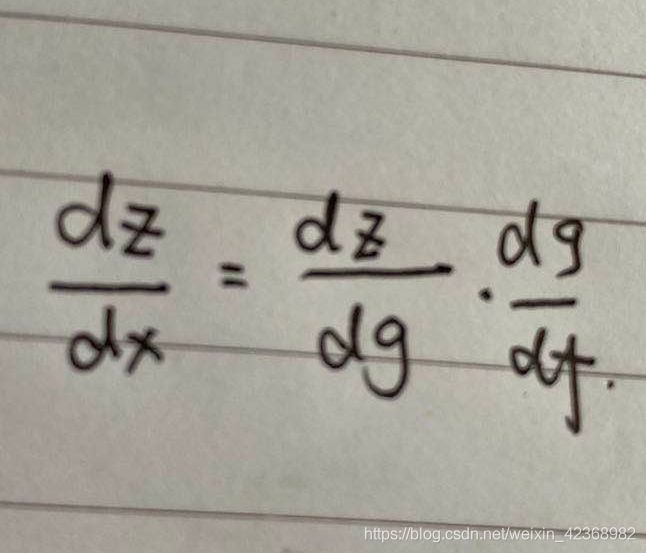链式法则---微积分链式法则和概率链式法则

本篇介绍了微积分链式法则和概率链式法则。

一、概率链式法则

     这里首先给出概率链式法则的公式：N个事件的概率链式法则如下，
    P(X1, X2, ... Xn) = P(X1 | X2, X3 ... Xn) * P(X2 | X3, X4 ... Xn) ... P(Xn-1 | Xn) * P(Xn)。

     概率链式法则的作用特别体现在，当我们的事件存在独立相关性的情况下。比如说，当A和B两个事件相互独立时，P(A|B)=P(A)。
     当A、B相互独立，并把它推广到三个事件时，有P(A|B,C)=P(A|C)=P(B|C)。其中P(A|B,C)表示在B和C事件都发生的情况下，A事件发生的概率。由条件概率（P(A|B)）的定义我们知道，条件概率是指事件A在另外一个事件B已经发生条件下的发生概率。这里既然A与B相互独立，那B就不是A是否发生的条件，A就只与C有关。

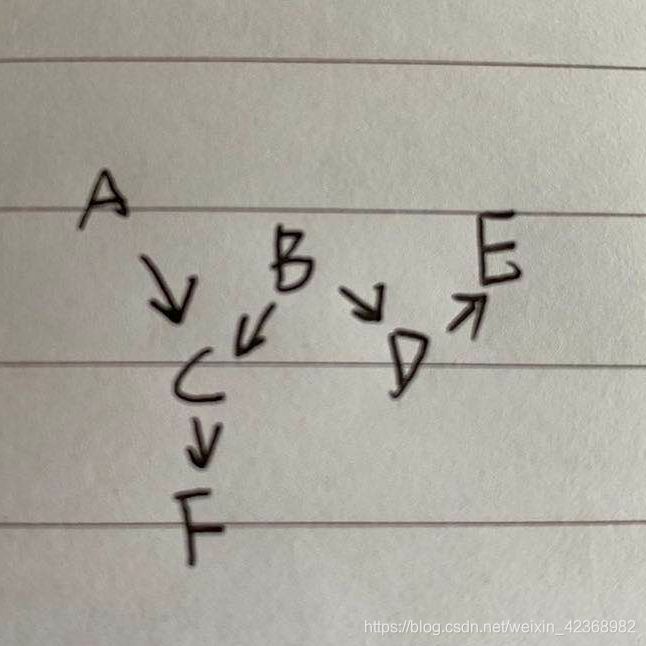
     假设有事件ABCDEF，箭头表示它们之间存在的依赖关系，其中F只和C有关，E只和D有关，D只和B有关，C和A、B有关。假设这里要求ABCEDF事件同时发生的概率P（A,B,C,D,E,F）是多大？
     这里完整的公式是这样的：
     P（A,B,C,D,E,F）=P（F|A,B,C,D,E）*P（A,B,C,D,E）
                                  =P（F|A,B,C,D,E）*P（C|A,B,D,E）*P（A,B,D,E）
                                  =P（F|A,B,C,D,E）*P（C|A,B,D,E）*P（E|A,B,D）*P（A,B,D）
                                  =P（F|A,B,C,D,E）*P（C|A,B,D,E）*P（E|A,B,D）*P（D|A,B）*P（A,B）
                                  =P（F|A,B,C,D,E）*P（C|A,B,D,E）*P（E|A,B,D）*P（D|A,B）*P（A|B）*P（B）

  但是利用事件的独立性，上面复杂的式子可以简化为：
  P（A,B,C,D,E,F）=P（F|C）*P（C|A,B）*P（E|D）*P（D|B）*P（A）*P（B）

事件的独立性：

 1.F只和C有关，P（F|A,B,C,D,E）=P（F|C）
 2.C只和A、B有关，P（C|A,B,D,E）=P（C|A,B）
 3.A和B无关，P（A|B）=P（A）
 4.E只和D有关，P（E|A,B,D）=P（E|D）
 5.D只和B有关，P（D|A,B）=P（D|B）

二、微积分链式法则

     微积分链式法则主要是用于计算复合函数的导数。在BP算法中，我们就会用到微积分链式法则，这是一种高效的特定运输顺序。下面是problem formulation：
   假设实数x，f(·)和g(·)是从实数映射到实数的函数。若y=f(x)，z=g(f(x))，则微分链式法则为：