机器学习|深度学习|重磅推出---全网最全Numpy简明教程（一）

本教程面向初学者的Numpy简明教程，学好Numpy才能在深度学习、机器学习、AI等领域进军，如果感觉此文不错，欢迎和博主交流探讨

1、Numpy介绍

Numeric Python 数字的Python

NumPy系统是Python的一种开源的数值计算扩展

1. 一个强大的N维数组对象ndarray
2. 拥有比较成熟的函数库
3. 用于整合C/C++和Fortran代码的工具包
4. 可以实现线性代数、傅里叶变换和随机数生成函数
5. Numpy和稀疏矩阵运算包Scipy配合使用更加强大

Numpy主要用于数组的计算，主要应用于机器学习和深度学习领域，所有我们就有必要了解AI的本质是什么

现在的AI模型本质上是在进行数学运算
数学运算中主要是在做矩阵运算
在计算机中，最擅长做计算
矩阵的计算比较快，我们可以通过一定的方法，把生活中的事物，抽象成矩阵

Numpy中提供了一种数据类型：ndarray数组，nd—>n dimension n个维度
当然，在Python中，列表也是可以表示多维数组
但是，Python中列表存在缺陷：

1. 查询速度慢
   

2. 占用空间大

# 导入numpy库，并查看numpy版本  
# 为什么需要关注版本信息？  因为有些情况下，版本会出现不兼容情况  
import numpy as np  
print(np.__version__)  
  
# __sizeof__是Python提供的魔术方法，可以查看对象的占用内存  
lst1 = [i for i in range(10000)]  
print(lst1.__sizeof__())  
  
nd1 = np.array([i for i in range(10000)])  
print(nd1.__sizeof__())

单下划线开头：一般用于类内的私有属性或方法
双下划线开头：一般为Python内置的属性，不推荐你自己的代码使用双下划线开头
双下划线开头和单下划线结尾：Python内置的魔术方法或属性

2、创建ndarray数组

在创建ndarray数组之前，需要先导入Numpy这个包

import numpy as np  
print(np.__version__)  # 查看版本信息

创建ndarray数组可以使用：

1. 列表
2. routines函数 常规函数

2.1、np.array

# 导入numpy库，并查看numpy版本  
# 为什么需要关注版本信息？  因为有些情况下，版本会出现不兼容情况  
import numpy as np  
print(np.__version__)  
  
# 参数为一个列表  
nd1 = np.array([1, 2, 3])  
  
print(nd1, type(nd1))  
  
# 将ndarray转换为list  
lst1 = nd1.tolist()  
print(lst1, type(lst1))  
  
# 假设使用np.array()创建ndarray数组，参数中传递不一样的数据类型  
# 会将数据类型转换为统一的数据类型  
nd2 = np.array([1.2, 1, 3])  
print(nd2, nd2.dtype)

2.2、np.ones

创建一个ndarray数组，里面元素全部为1

order这个参数直接默认值就可以，一般不用去修改

one表示1，加一个s，表示里面存在很多1

import numpy as np  
print(np.__version__)  
  
# shape指定创建ndarray形状，默认创建出来ndarray的dtype为float  
# dtype指定数据类型  
nd1 = np.ones(shape=(3, 4))
print(nd1, type(nd1))

nd2 = np.ones(shape=(3, 4), dtype=np.int32)
print(nd2, type(nd2))

2.3、np.zeros

参考上一个routine函数：np.ones
一个是创建一个全是0的数组
一个是创建一个全为1的数组

import numpy as np
print(np.__version__)  # 查看版本信息

nd1 = np.zeros(shape=(4, 2))
print(nd1, type(nd1))

2.4、np.full

用指定元素进行填充

import numpy as np
print(np.__version__)  # 查看版本信息

nd1 = np.full(shape=(4, 3), fill_value=10)
print(nd1)

2.5、np.eye

import numpy as np
print(np.__version__)  # 查看版本信息

# 生成一个二维矩阵，对角线上全部为1（需要列和行相等），其余位置为0  
# k控制主对角线，往上走几下  
nd1 = np.eye(4, 4, k=0)
nd2 = np.eye(4, 4, k=1)
nd3 = np.eye(4, 4, k=2)

print(nd1)
print(nd2)
print(nd3)

方阵：行数和列数相同的矩阵
单位矩阵：在方阵的基础上，主对角线上全部为1，其他位置全是0的方阵
满秩矩阵：如果一个矩阵可以变为单位矩阵，那么我们把这个矩阵叫做满秩矩阵

2.6、np.linspace

import numpy as np
print(np.__version__)  # 查看版本信息

# 创建一个等差数列  
# def linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None,  
#              axis=0):  
# endpoint=True默认包括stop值  
# retstep=False默认不显示间隔  
nd1 = np.linspace(1, 10, num=10)
print(nd1)

nd2 = np.linspace(1, 10, num=10, retstep=True)
print(nd2)

2.7、np.arange

和Python中的range()函数类似

import numpy as np
print(np.__version__)  # 查看版本信息

nd1 = np.arange(10)
print(nd1)

当使用非整数步长(如0.1)时，结果通常不一致。最好使用numpy。这些情况下的Linspace
小数会带来数据的不准确，当需要使用小数作为步长的时候，最好使用“numpy.linspace”

2.8、np.random.randint

在Python中，不存在真正的随机数，随机数是通过当前系统时间，作为时间戳，当作种子，放入算法，算出时间。
当，随机数种子固定，每次产生随机数字一致

import numpy as np
print(np.__version__)  # 查看版本信息

nd1 = np.random.randint(1, 10, size=(4, 2))
print(nd1)

Numpy中的random.randint和Python中的random.randint几乎一样，都是产生随机整数
但是，Numpy中的random.randint指定的整数为左闭右开
Python中的random.randint为全闭区间

2.9、np.random.random

产生[ 0,1 ) 之间的小数

import numpy as np
print(np.__version__)  # 查看版本信息

nd1 = np.random.random(size=(4, 2))
print(nd1)

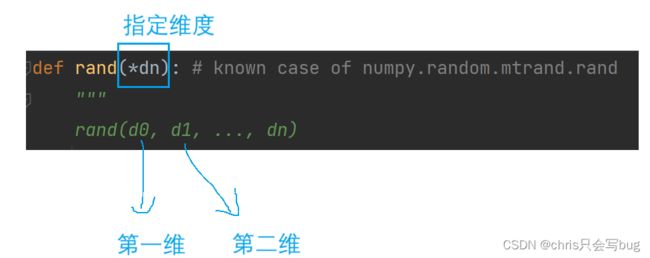
2.10、np.random.rand

类似于np.random.random

import numpy as np

print(np.__version__)

nd1 = np.random.rand(3, 2)
print(nd1)
print(nd1.mean())  # 求均值

2.11、np.random.normal

创建正太分布（高斯分布）

首先，我们需要了解什么是正太分布（高斯分布）？

import numpy as np
print(np.__version__)  # 查看版本信息

# 给出的数据越多，最后计算出的均值就越接近于给定均值
nd1 = np.random.normal(1, 3, size=(4, 4))
print(nd1)
print(nd1.mean())  # 求均值

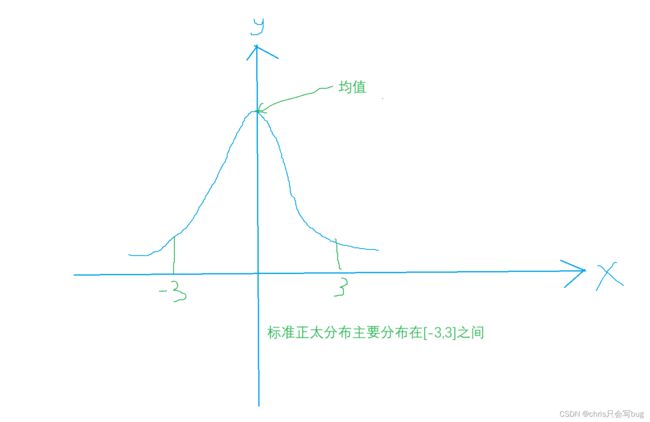
2.12、np.random.randn

生成一个标准正太分布的ndarray数组

首先，我们需要了解什么是标准正太分布？

import numpy as np
print(np.__version__)  # 查看版本信息

nd1 = np.random.randn(4, 3)
print(nd1)
print(nd1.mean())  # 求均值

3、ndarray属性

4个必须记住的ndarray属性：

1. ndim 维度 dimension
   维度可以使用ndim查看，也可以打印出ndarray数组，查看几层中括号，有2层，就是二维数组
2. shape 形状（每一个维度的长度）
3. size 总长度（每一个维度的长度相乘）
4. dtype 元素类型

import numpy as np

print(np.__version__)

# def full(shape, fill_value, dtype=None, order='C'):
nd1 = np.full(shape=(4, 3), fill_value=20)
print(nd1)

# dimension维度
print(nd1.ndim)

# shape形状
print(nd1.shape)

# 元素个数  
print(nd1.size)

# 元素数据类型
print(nd1.dtype)