一个非常简单的变分量子分类器 （VQC）

一、说明

        在之前的帖子（这里和这里）中，我已经开始谈论 QML，为什么以及如何学习，从现在开始，我将开始分享我的研究和发现，到目前为止，这些都是非常基本的。

二、实验概述

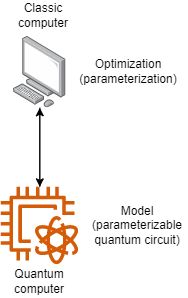
        今天，我将设计一个变分量子分类器 （VQC），它是一个混合计算分类器，如图 1 所示。

图 1 — 混合计算图

        在这里，量子计算机配置了一个可参数化的量子电路，这与我们在经典分类问题（例如逻辑回归、SVM 等）中用作模型的数学函数相似。经典计算机负责进行优化，因此它设置电路参数，运行量子计算机，收集结果并根据损失函数细化参数。因此，这里唯一的区别是，我们没有使用我们的日常分类算法，而是使用量子电路作为模型（又名ansatz）。

        然而，尽管看起来很简单，但围绕这种混合计算架构存在挑战。正如我在第一篇文章中提到的，经典计算和量子计算有不同的范式，所以我们的量子电路必须有一些阶段。

图 2 — 量子电路的各个阶段

        特征图是电路的第一阶段，其中经典数据必须编码为量子比特。有很多编码方法，因为特征图是从向量空间到另一个向量空间（希尔伯特空间）的数学转换。研究人员一直在研究如何为每个问题找到最佳映射，即将映射本身变成优化问题。这是相当有趣的，因为一个好的映射意味着不同类的数据之间的良好分离，这大大简化了分类问题。Pennylane在这里和这里有一些有趣和基本的阅读材料。不幸的是，Qiskit已经弃用了aqua，但他们在这里也有一些功能图。

        我也想潜入并阅读这篇文章。

        在第二阶段，我们设计一个量子电路，它将成为我们的模型，在这里我们可以随心所欲地发挥创造力，但我们必须考虑到同样的旧规则仍然很重要：不要对简单的问题使用太多参数以避免过度拟合，也不要使用太少的参数来避免偏见，正如我们已经知道的那样。但最重要的是：既然我们使用的是量子计算，就必须使用叠加和纠缠，以便从量子计算范式中汲取精华。

        量子电路在某种程度上既简单又棘手，因为它们是线性变换，但作为组件化电路进行分析，这需要注意。正如我在上一篇文章中提到的，Frank Zickert的书和博客是我阅读的了解量子电路的最佳参考资料。

三、要解决问题

        在对VQC有基本的了解之后，在这篇文章中，我们将设计一个基于Kaggle的泰坦尼克号数据集的分类器。在那里，我们有关于乘客的信息，以及他们是否幸存下来。

        此数据集中的变量包括：

• 乘客识别
• 乘客姓名
• 头等舱（一、二、三）
• 性
• 年龄
• SibSP（兄弟姐妹和/或配偶）
• 帕奇（父母或孩子在船上）
• 票
• 票价
• 舱
• 已启程
• 幸存

        在这里，我们正在构建一个分类器，根据乘客的特征预测乘客是否幸存下来。我不打算深入研究功能分析和选择，因为这不是本文的重点，所以我将跳到选定的变量：

• is_child（如果年龄<12）
• is_class1（如果人是头等舱）
• is_class2
• is_female

        基本上，头等舱的儿童和妇女的存活率更高。此外，第二类和第三类的存活率下降。这里所有的变量都是布尔值，这很好，因为这是一个非常简单的模型，这也将大大简化我们的特征图选择。

四、要素嵌入和映射

        我认为这篇Pennylane文章是对量子嵌入的一个非常好的介绍，因为它表明不同的方法有内在的优缺点。基嵌入可能是最简单的嵌入，但同时在量子比特方面可能代价高昂。振幅嵌入提供了重要的量子位节省，但它可能具有压缩的向量空间和类之间的不良分离。

        由于我们只使用四个变量，为了简单起见，我将使用基础嵌入，而无需进一步的映射电路。

        在这种情况下，我们只需将经典位转换为其等效量子比特。因此，如果我们的四个变量是 1010，这将转换为 |1010>。

五、模特（安萨茨）

        ansatz是设计为我们模型的可参数化量子电路。正如我之前提到的，这个电路必须具有一定程度的叠加和纠缠，才能证明在我们的项目中使用量子器件是合理的。

        所选电路如图所示：

图 3 — 泰坦尼克号分类器的安萨茨

        这是我从Pennylane的例子中获取的常见电路。如果你没有研究过量子电路，它可能看起来很复杂，但这个想法相当简单。这是一个两层电路，因为核心结构重复了2次。首先，我们对每个量子比特围绕 Z、Y 和 Z 轴旋转，这里的想法是分别在每个量子比特上插入一定程度的叠加。这些旋转是参数化的，在算法的每次交互中，这些参数将由经典计算机更新。此外，我们谈论的是 Y 轴和 Z 轴上的旋转，因为量子比特的矢量空间是一个球体（布洛赫球体）。RZ 只会改变量子比特相位，RY 会影响量子比特与 |0> 和 |1> 的接近程度。

        之后，我们在每对量子比特之间有四个受控非（CNOT）状态，这是一个量子门，根据另一个量子比特的状态（分别为目标和控制）反转量子比特状态。因此，这个门纠缠了我们电路中的所有量子位，现在所有状态都被纠缠在一起。在第二层中，我们应用了一组新的旋转，这不仅仅是第一层的逻辑重复，因为现在所有状态都纠缠在一起，这意味着旋转第一个量子比特也会影响其他量子比特！最后，我们有一套新的 CNOT 门。

        这是对我们电路的一个非常简单的解释，但通过一些研究和实践，这些概念会对你来说很直观（我承认我仍然在这个学习过程中！

六、优化

        在这个项目中，我使用的是Pennylane的Adam Optimizer（在上一篇文章中，我说我正在使用Qiskit，但是我对已弃用的函数有一些问题，所以我回到了Pennylane）。我测试了学习率，直到找到一个平滑收敛到我们最佳水平的学习率。

七、代码和结果

        我使用带有量子比特模拟器的Pennylane实现了代码。我承认我从教程中获得了代码的大部分量子部分，并在优化器中进行了一些更改，因为原始代码使用了 Nesterov 动量优化器，并且我与 Adam 有更好的结果和收敛。

import pennylane as qml
from pennylane import numpy as np
from pennylane.optimize import AdamOptimizer

from sklearn.model_selection import train_test_split
import pandas as pd

from sklearn.metrics import accuracy_score
from sklearn.metrics import f1_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score

import math

num_qubits = 4
num_layers = 2

dev = qml.device("default.qubit", wires=num_qubits)

# quantum circuit functions
def statepreparation(x):
    qml.BasisEmbedding(x, wires=range(0, num_qubits))

def layer(W):

    qml.Rot(W[0, 0], W[0, 1], W[0, 2], wires=0)
    qml.Rot(W[1, 0], W[1, 1], W[1, 2], wires=1)
    qml.Rot(W[2, 0], W[2, 1], W[2, 2], wires=2)
    qml.Rot(W[3, 0], W[3, 1], W[3, 2], wires=3)

    qml.CNOT(wires=[0, 1])
    qml.CNOT(wires=[1, 2])
    qml.CNOT(wires=[2, 3])
    qml.CNOT(wires=[3, 0])

@qml.qnode(dev, interface="autograd")
def circuit(weights, x):

    statepreparation(x)

    for W in weights:
        layer(W)

    return qml.expval(qml.PauliZ(0))

def variational_classifier(weights, bias, x):
    return circuit(weights, x) + bias

def square_loss(labels, predictions):
    loss = 0
    for l, p in zip(labels, predictions):
        loss = loss + (l - p) ** 2

    loss = loss / len(labels)
    return loss

def accuracy(labels, predictions):

    loss = 0
    for l, p in zip(labels, predictions):
        if abs(l - p) < 1e-5:
            loss = loss + 1
    loss = loss / len(labels)

    return loss

def cost(weights, bias, X, Y):
    predictions = [variational_classifier(weights, bias, x) for x in X]
    return square_loss(Y, predictions)

# preparaing data
df_train = pd.read_csv('train.csv')

df_train['Pclass'] = df_train['Pclass'].astype(str)

df_train = pd.concat([df_train, pd.get_dummies(df_train[['Pclass', 'Sex', 'Embarked']])], axis=1)

# I will fill missings with the median
df_train['Age'] = df_train['Age'].fillna(df_train['Age'].median())

df_train['is_child'] = df_train['Age'].map(lambda x: 1 if x < 12 else 0)
cols_model = ['is_child', 'Pclass_1', 'Pclass_2', 'Sex_female']

X_train, X_test, y_train, y_test = train_test_split(df_train[cols_model], df_train['Survived'], test_size=0.10, random_state=42, stratify=df_train['Survived'])

X_train = np.array(X_train.values, requires_grad=False)
Y_train = np.array(y_train.values * 2 - np.ones(len(y_train)), requires_grad=False)

# setting init params
np.random.seed(0)
weights_init = 0.01 * np.random.randn(num_layers, num_qubits, 3, requires_grad=True)
bias_init = np.array(0.0, requires_grad=True)

opt = AdamOptimizer(0.125)
num_it = 70
batch_size = math.floor(len(X_train)/num_it)

weights = weights_init
bias = bias_init
for it in range(num_it):

    # Update the weights by one optimizer step
    batch_index = np.random.randint(0, len(X_train), (batch_size,))
    X_batch = X_train[batch_index]
    Y_batch = Y_train[batch_index]
    weights, bias, _, _ = opt.step(cost, weights, bias, X_batch, Y_batch)

    # Compute accuracy
    predictions = [np.sign(variational_classifier(weights, bias, x)) for x in X_train]
    acc = accuracy(Y_train, predictions)

    print(
        "Iter: {:5d} | Cost: {:0.7f} | Accuracy: {:0.7f} ".format(
            it + 1, cost(weights, bias, X_train, Y_train), acc
        )
    )

X_test = np.array(X_test.values, requires_grad=False)
Y_test = np.array(y_test.values * 2 - np.ones(len(y_test)), requires_grad=False)

predictions = [np.sign(variational_classifier(weights, bias, x)) for x in X_test]

accuracy_score(Y_test, predictions)
precision_score(Y_test, predictions)
recall_score(Y_test, predictions)
f1_score(Y_test, predictions, average='macro')

        我还做了一些测试，改变了我们的ansatz中的层数，似乎2层是我们在这里的最佳结果。对于一层，我们没有第二个旋转，这会产生纠缠的超位，这导致了偏差，因为我们的模型预测的结果总是相同的（不是存活的，大多数目标类），并且对于更多的层，我没有更好的结果，主要是因为我们的问题很简单，更多的参数会导致我们过度拟合。

        我们的模型有以下结果：

•         准确度：78.89%
•         精度： 76.67%
•         召回率：65.71%
•         F1： 77.12%

        这些都是可靠的结果，模型是预测而不是猜测大多数结果。但是我们可以将我们的VQC与经典算法进行比较，所以我训练了一个逻辑回归，并得到了以下结果：

•         准确度：75.56%
  •         精度： 69.70%
    •         召回率：65.71%
      •         F1： 74.00%

        我们的VQC性能略好于逻辑回归模型！好吧，这并不意味着 VQC 一定更好，只是这个具有特定优化过程的特定模型表现得更好。但这篇文章的主要思想是表明构建量子分类器很简单，尽管这没什么了不起的，但这是对 QML 的简单有效的使用。马修斯·卡马罗萨诺·伊达尔戈