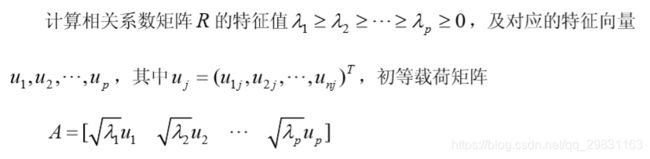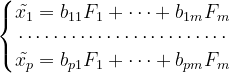因子分析 factor analysis (六) ：用因子分析法进行综合评价
因子分析系列博文:
因子分析 factor analysis (一 )：模型的理论推导
因子分析 factor analysis (二 ) ： 因子分析模型
因子分析 factor analysis (三) ： 因子载荷矩阵的估计方法
因子分析 factor analysis (四) ： 因子旋转（正交变换）
因子分析 factor analysis (五) ： 因子得分
因子分析 factor analysis (六) ：用因子分析法进行综合评价
因子分析 factor analysis (七) ：因子分析法与主成分分析的异同
目录
因子分析的步骤
1.对原始数据进行标准化处理
2．计算相关系数矩阵R
3．计算初等载荷矩阵
4．选择m （ m≤ p）个主因子，进行因子旋转
5.计算因子得分，并进行综合评价
6. 利用综合因子得分公式 计算各样本的综合得分
二 例题
一 因子分析的步骤
1．选择分析的变量
用定性分析和定量分析的方法选择变量，因子分析的前提条件是观测变量间有较强 的相关性，因为如果变量之间无相关性或相关性较小的话，他们不会有共享因子,所以 原始变量间应该有较强的相关性。
2．计算所选原始变量的相关系数矩阵
相关系数矩阵描述了原始变量之间的相关关系。可以帮助判断原始变量之间是否存 在相关关系，这对因子分析是非常重要的，因为如果所选变量之间无关系，做因子分析 是不恰当的。并且相关系数矩阵是估计因子结构的基础。
3．提出公共因子
这一步要确定因子求解的方法和因子的个数。需要根据研究者的设计方案或有关的 经验或知识事先确定。因子个数的确定可以根据因子方差的大小。只取方差大于1(或特 征值大于1)的那些因子，因为方差小于1的因子其贡献可能很小；按照因子的累计方差 贡献率来确定，一般认为要达到60％才能符合要求。
4．因子旋转
通过坐标变换使每个原始变量在尽可能少的因子之间有密切的关系，这样因子解的 实际意义更容易解释,并为每个潜在因子赋予有实际意义的名字。
5．计算因子得分
求出各样本的因子得分，有了因子得分值，则可以在许多分析中使用这些因子，例 如以因子的得分做聚类分析的变量，做回归分析中的回归因子。
1.对原始数据进行标准化处理
2．计算相关系数矩阵R
3．计算初等载荷矩阵
4．选择m （ m≤ p）个主因子，进行因子旋转
根据初等载荷矩阵，计算各个公共因子的贡献率，并选择m 个主因子。对提取的因子载荷矩阵进行旋转，得到矩阵
(其中
为A的前m列，T为正交矩阵），构造因子模型
5.计算因子得分，并进行综合评价
我们用回归方法求单个因子得分函数 
记
；则有
![\large \left [ b_{1}^{T} \: b_{2}^{T} ... \: b_{m}^{T}\right ] =R^{-1}A](http://img.e-com-net.com/image/info8/969d02d994af4ff9b7c0339cd32df92c.gif){kind=small}
6. 利用综合因子得分公式 计算各样本的综合得分
-
二 例题
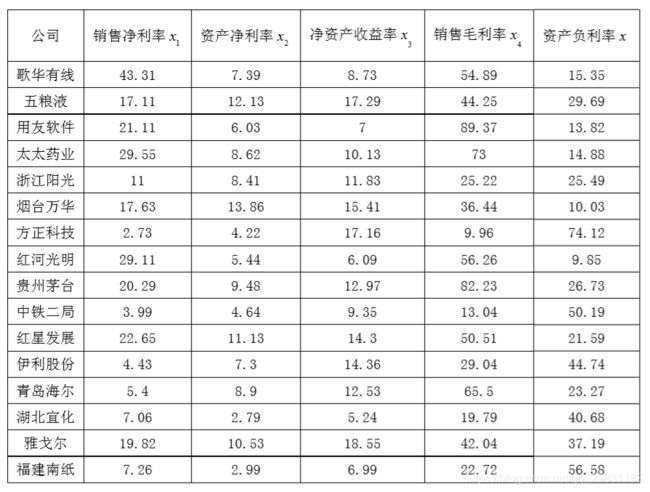
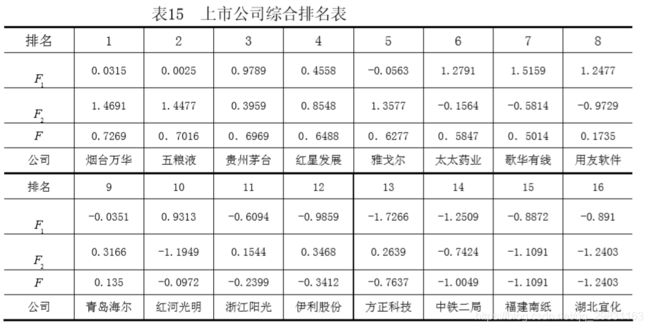
已知部分上市公司的数据见下表，试用因子分析法对上述企业进行综合评价。
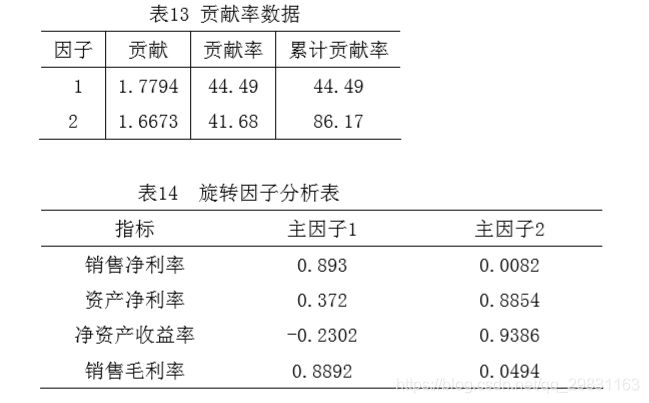
解 按上述步骤计算得旋转后的因子贡献及贡献率见表13、因子载荷阵见表14。
我们通过相关分析，在显著水平为0.05的情况下，得出赢利能力F 与资产负债率 x 之间的相关系数为-0.6987，这表明两者存在中度相关关系。因子分析法的回归方程为：F = 0.829-0.0268X
回归方程在显著性水平0.05的情况下，通过了假设检验。
计算的MATLAB程序如下：
clc,clear
load data.txt %把原始数据保存在纯文本文件data.txt中
data=reshape(data,[16,5]);
m=size(data,1);
x=data(:,5);data=data(:,1:4),num=2;
data=zscore(data); %数据标准化
r=cov(data);
[vec,val,con]=pcacov(r); %进行主成分分析的相关计算
val,con
f1=repmat(sign(sum(vec)),size(vec,1),1);
vec=vec.*f1; %特征向量正负号转换
f2=repmat(sqrt(val)',size(vec,1),1);
a=vec.*f2 %载荷矩阵
%如果指标变量多，选取的主因子个数少，可以直接使用factoran进行因子分析
%本题中4个指标变量，选取2个主因子，factoran无法实现
[b,t]=rotatefactors(a(:,1:num),'method', 'varimax') %旋转变换
bz=[b,a(:,num+1:end)] %旋转后的载荷矩阵
gx=sum(bz.^2) %计算因子贡献
gxv=gx/sum(gx) %计算因子贡献率
dfxsh=inv(r)*b %计算得分函数的系数
df=data*dfxsh %计算各个因子的得分
zdf=df*gxv(1:num)'/sum(gxv(1:num)) %对各因子的得分进行加权求和
[szdf,ind]=sort(zdf,'descend') %对企业进行排名
xianshi=[df(ind,:)';zdf(ind)';ind'] %显示计算结果
[x_zdf_coef,p]=corrcoef([zdf,x]) %计算相关系数
[d1,d1int,d2,d2int,stats]=regress(zdf,[ones(m,1),x]) %回归分析计算 因子分析系列博文:
因子分析 factor analysis (一 )：模型的理论推导
因子分析 factor analysis (二 ) ： 因子分析模型
因子分析 factor analysis (三) ： 因子载荷矩阵的估计方法
因子分析 factor analysis (四) ： 因子旋转（正交变换）
因子分析 factor analysis (五) ： 因子得分
因子分析 factor analysis (六) ：用因子分析法进行综合评价
因子分析 factor analysis (七) ：因子分析法与主成分分析的异同