力扣高频|算法面试题汇总(九):动态规划
力扣高频|算法面试题汇总(一):开始之前
力扣高频|算法面试题汇总(二):字符串
力扣高频|算法面试题汇总(三):数组
力扣高频|算法面试题汇总(四):堆、栈与队列
力扣高频|算法面试题汇总(五):链表
力扣高频|算法面试题汇总(六):哈希与映射
力扣高频|算法面试题汇总(七):树
力扣高频|算法面试题汇总(八):排序与检索
力扣高频|算法面试题汇总(九):动态规划
力扣高频|算法面试题汇总(十):图论
力扣高频|算法面试题汇总(十一):数学&位运算
力扣高频|算法面试题汇总(九):动态规划
力扣链接
目录:
- 1.至少有K个重复字符的最长子串
- 2.二叉树中的最大路径和
- 3.最长连续序列
- 4.打家劫舍
- 5.完全平方数
- 6.最长上升子序列
- 7.零钱兑换
- 8.矩阵中的最长递增路径
1.至少有K个重复字符的最长子串
找到给定字符串(由小写字符组成)中的最长子串 T , 要求 T 中的每一字符出现次数都不少于 k 。输出 T 的长度。
示例 1:
输入:
s = “aaabb”, k = 3
输出:
3
最长子串为 “aaa” ,其中 ‘a’ 重复了 3 次。
示例 2:
输入:
s = “ababbc”, k = 2
输出:
5
最长子串为 “ababb” ,其中 ‘a’ 重复了 2 次, ‘b’ 重复了 3 次。
思路:
参考大佬的思路,简单易懂:多路分治的递归方法。
总结一下:
1.建立一个哈希表,记录每个字符的出现次数。
2.遍历数组,根据哈希表判断该字符出现的次数,如果小于k,则记录,放入split数组中。因为这个字符出现的次数小于k,则必不可能构成满足题意的字符串,则可以根据该字符的位置对字符串进行分割。
3.边界条件:分割的split长度为0,即该子字符串均满足重复次数大于k的条件。
4.递归:对分割的字符串进一步递归求解。
5.trick:如果子字符串的长度小于当前答案,则不必继续递归,因为不可能再出现比当前结果更大的子字符串了。
C++:
class Solution {
public:
int longestSubstring(string s, int k) {
unordered_map<char, int> countHash; // 哈希表
vector<int> split; // 分割的节点的位置
for(auto c : s) ++countHash[c];// 记录出现的次数
for(int i = 0; i < s.length(); ++i)
if(countHash[s[i]] < k)
split.push_back(i); // 记录分割的位置
if(split.size() == 0) return s.length();// 边界条件
int res = 0; // 答案
int left = 0;
int len;
split.push_back(s.length());// !!!这个很重要,因为需要判断到字符串的最后一个位置
for(int i = 0; i < split.size(); ++i){
len = split[i] - left;
if(len > res)// 还有可能有答案,继续递归
res = max(longestSubstring(s.substr(left, split[i]), k), res);
left = split[i] + 1;
}
return res;
}
};
Python:
class Solution:
def longestSubstring(self, s: str, k: int) -> int:
countHash = {}
for c in s:
if not c in countHash:
countHash[c] = 1
else:
countHash[c] += 1
split = []
for i in range(len(s)):
if countHash[s[i]] < k:
split.append(i)
if len(split) == 0:
return len(s)
split.append(len(s))
res = 0
left = 0
for i in split:
length = i - left
if length > res:
res = max(self.longestSubstring(s[left:i], k), res)
left = i + 1
return res
2.二叉树中的最大路径和
给定一个非空二叉树,返回其最大路径和。
本题中,路径被定义为一条从树中任意节点出发,达到任意节点的序列。该路径至少包含一个节点,且不一定经过根节点。
示例 1:
输入: [1,2,3]
1
/
2 3
输出: 6
示例 2:
输入: [-10,9,20,null,null,15,7]
-10
/
9 20
/
15 7
输出: 42
思路:
使用递归,参考官方图示:

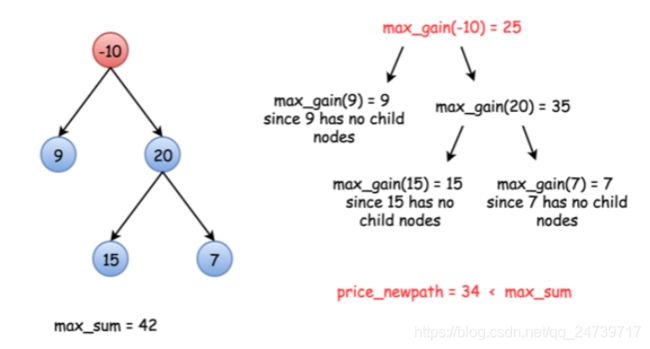
总结一下:
1.需要一变量来保存局部最大值。每次递归都会和这个局部最大值进行比较,如果大于这个局部最大值,则会更新。
2.递归的边界条件是遇到空节点,这个时候返回0即可,不影响结果。
3.需要对根节点的左右子树进行递归,获取其最大值。如果左右子树最大值小于0,则不如不包含其路径,舍去,记为0即可。
4.如果当前根节点的值和左右子树的最大值大于局部最大值,则更新局部最大值。
5.最后需要返回单边最大值(有点回溯的意思)。
复杂度分析:
时间复杂度: O ( N ) O(N) O(N)其中 NN 是结点个数。我们对每个节点访问不超过 2 次。
空间复杂度: O ( l o g ( N ) ) O(log(N)) O(log(N))。需要一个大小与树的高度相等的栈开销,对于二叉树空间开销是 O ( l o g ( N ) ) O(log(N)) O(log(N))。
C++
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int maxPathSum(TreeNode* root) {
int max_val = INT_MIN;
maxPathSumCore(root, min_val);
return max_val ;
}
int maxPathSumCore(TreeNode* root, int& val){
if(root == NULL) return 0; // 边界条件 遇到空节点
int leftMax = max(0, maxPathSumCore(root->left, val)); // 递归左子树,如果为负数,不如为0
int rightMax = max(0, maxPathSumCore(root->right, val)); // 递归右子树
val = max(val, root->val + leftMax + rightMax); // 计算局部最大值
// 返回经过root的单边,最大分支给上游
return root->val + max(leftMax, rightMax);
}
};
Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def maxPathSum(self, root: TreeNode) -> int:
self.Val = float('-inf') # 负无穷
self.maxPathSumCore(root)
return self.Val
def maxPathSumCore(self, root):
if root == None:
return 0
leftMax = max(0, self.maxPathSumCore(root.left))
rightMax = max(0, self.maxPathSumCore(root.right))
self.Val = max(self.Val, root.val + leftMax + rightMax)
return root.val +max(leftMax, rightMax)
3.最长连续序列
给定一个未排序的整数数组,找出最长连续序列的长度。
要求算法的时间复杂度为 O(n)。
示例:
输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。
思路:
暴力枚举。第一个for循环,获取一个数字,第二个for循环判断以该数字开头,是否存在连续序列,每次判断需要花费O(n)的时间在数字中查找,整个时间复杂度为 O ( n 3 ) O(n^3) O(n3),空间复杂度为 O ( 1 ) O(1) O(1)。肯定会超时,就没做这个了。
思路2:
排序。通过排序,则序列有序,只需要判断满足nums[i] == nums[i-1]+1的长度。参考官方图示:
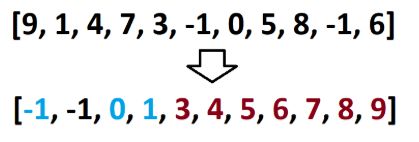
时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn),标准的排序算法时间复杂度。空间复杂度: O ( 1 ) O(1) O(1)或 O ( n ) O(n) O(n)。如果允许对原数组进行改动,则是常数空间复杂度,如果不允许,则需要一个副本。
思路3:
哈希表和线性空间的构造。使用一个哈希表(或集合)记录每个元素。然后遍历记录集合,首先判断num-1是否在集合中,如果不在则开始计算(因为需要保证num是整个序列的开头),不断使num+1,查找是否存在在集合中,如果存在则结果+1。
C++
class Solution {
public:
int longestConsecutive(vector<int>& nums) {
if(nums.size() <= 1) return nums.size();
// 集合存储数字
unordered_set<int> nums_set(nums.begin(), nums.end());
int res = 1;
// 遍历集合
for(auto num: nums_set){
// 需要保证num是序列的开头。
if( nums_set.find(num - 1) == nums_set.end()){
int count = 1;
int cur_num = num + 1;
while(nums_set.find(cur_num) != nums_set.end()){
++count;
++cur_num;
}
res = max(res, count);
}
}
return res;
}
};
Python:
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
nums_set = set(nums)
if len(nums)<=1:
return len(nums)
res = 1
for num in nums_set:
if not (num -1) in nums_set:
cur_num = num+1
count = 1
while cur_num in nums_set:
cur_num += 1
count += 1
res = max(res, count)
return res
4.打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
思路:
参考官方思路:
1.当n=1时,抢劫的钱为: f ( 1 ) = A 1 f(1) = A_1 f(1)=A1。
2.当n=2时,抢劫的钱为: f ( 2 ) = m a x ( A 1 , A 2 ) f(2) = max(A_1, A_2) f(2)=max(A1,A2)
3.当n=3时,这时有两个选择,一个是:选择第第一个和第三个房子,另一个是选择第二个房子。整体而言, f ( 3 ) = m a x ( f ( 1 ) + A 3 , f ( 2 ) ) f(3)=max(f(1)+A_3, f(2)) f(3)=max(f(1)+A3,f(2))。
4.另 f ( − 1 ) = f ( 0 ) = 0 f(-1)=f(0)=0 f(−1)=f(0)=0,可得递推公式: f ( n ) = m a x ( f ( n − 1 ) , f ( n − 2 ) + A n ) f(n)=max(f(n-1),f(n-2)+A_n) f(n)=max(f(n−1),f(n−2)+An)。
复杂度分析:时间复杂度: O ( n ) O(n) O(n)。其中 n 为房子的数量。空间复杂度: O ( 1 ) O(1) O(1)。
C++
class Solution {
public:
int rob(vector<int>& nums) {
int pre = 0;
int cur = 0;
int res = 0;
for(auto num : nums){
res = max(pre+num, cur);
pre = cur;
cur = res;
}
return res;
}
};
Python:
class Solution:
def rob(self, nums: List[int]) -> int:
cur = 0
pre = 0
res = 0
for num in nums:
res = max(pre + num, cur)
pre = cur
cur = res
return res
5.完全平方数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.
思路:
暴力递归(会超时)。本题的另外一种说法是:给定一个完全平方数列表和正整数 n,求出完全平方数组合成 n 的组合,要求组合中的解拥有完全平方数的最小个数。如官方题解所示,可以表示为一下公式:
n u m S q u a r e s ( n ) = m i n ( n u m S q u a r e s ( n − k ) + 1 ) ∀ k ∈ s q u a r e n u m b e r s numSquares(n)=min(numSquares(n-k) + 1) \qquad∀k∈square numbers numSquares(n)=min(numSquares(n−k)+1)∀k∈squarenumbers
可以有以下例程:
Python:
def numSquares(n):
# 计算n存在的所有平方数
square_nums = [i**2 for i in range(1, int(math.sqrt(n))+1)]
def minNumSquares(k):
""" recursive solution """
# bottom cases: find a square number
# 边界条件
if k in square_nums:
return 1
min_num = float('inf')
# 在所有可能的解决方案中找出最小值
for square in square_nums:
if k < square:
break
new_num = minNumSquares(k-square) + 1 # 不断递归
min_num = min(min_num, new_num)
return min_num
return minNumSquares(n)
思路2:
动态规划。
如官方题解所说,使用暴力枚举法会超出时间限制的原因很简单,因为重复的计算了中间解。解决递归中堆栈溢出的问题的一个思路就是使用动态规划(DP)技术,该技术建立在重用中间解的结果来计算终解的思想之上。要计算 n u m S q u a r e s ( n ) numSquares(n) numSquares(n)的值,首先要计算 n 之前的所有值,即 n u m S q u a r e s ( n − k ) ∀ k ∈ s q u a r e n u m b e r s numSquares(n-k) \qquad∀k∈square numbers numSquares(n−k)∀k∈squarenumbers。如果已经在某个地方保留了数字 n-k 的解,那么就不需要使用递归计算。
总结以下:
- 1.创建一个一维或多维数组 DP 来保存中间子解的值,以及通常数组最后一个值代表最终解。注意,创建了一个虚构的元素 dp[0]=0 来简化逻辑,这有助于在在余数 (n-k)恰好是一个完全平方数的情况下。
- 2.仍然需要计算
square_nums来保存所有小于n的所有平方数的集合。 - 3.从1开始循环到n,记录每个 n u m S q u a r e s ( i ) numSquares(i) numSquares(i)的值,并保存到DP数组中。
- 4.在循环结束时,返回数组中的最后一个元素作为解决方案的结果。
如官方图示,展示dp[4]和dp[5]的结果:

复杂度分析:
时间复杂度: O ( n ∗ n ) O(n*\sqrt{n}) O(n∗n),在主步骤中,我们有一个嵌套循环,其中外部循环是 n n n次迭代,而内部循环最多需要 n \sqrt{n} n 迭代。
空间复杂度: O ( n ) O(n) O(n),使用了一个一维数组 dp。
C++:
class Solution {
public:
int numSquares(int n) {
vector<int> squar_nums;
for(int i = 1; i < sqrt(n) + 1; ++i)
squar_nums.push_back(i*i);
vector<int> dp;
for(int i = 0; i < n + 1; ++i)
dp.push_back(INT_MAX);
dp[0] = 0;
for(int i = 1; i <n+1; ++i)
for(auto squar : squar_nums){
if(i < squar)
break;
dp[i] = min(dp[i], dp[i-squar] + 1);
}
return dp.back();
}
};
Python:
class Solution(object):
def numSquares(self, n):
"""
:type n: int
:rtype: int
"""
square_nums = [i**2 for i in range(0, int(math.sqrt(n))+1)]
dp = [float('inf')] * (n+1)
# bottom case
dp[0] = 0
for i in range(1, n+1):
for square in square_nums:
if i < square:
break
dp[i] = min(dp[i], dp[i-square] + 1)
return dp[-1]
思路3:
贪心枚举。
如官方题解所示,先定义一个名为 is_divided_by(n, count) 的函数,该函数返回一个布尔值,表示数字 n 是否可以被一个数字 count 组合,而不是像前面函数 numSquares(n) 返回组合的确切大小。
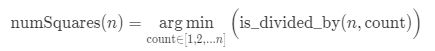
官方图示:

C++:
class Solution {
public:
set<int> squar_nums;
int numSquares(int n) {
for(int i = 1; i < sqrt(n) + 1; ++i)
squar_nums.insert(i*i);
for(int i =1; i <n+1;++i){
if(is_divided_by(n, i))
return i;
}
return n;
}
bool is_divided_by(int num, int count){
if(count == 1){
if(squar_nums.find(num) != squar_nums.end())
return true;
else
return false;
}
for(auto squar: squar_nums){
if(is_divided_by(num - squar, count - 1))
return true;
}
return false;
}
};
Python:
class Solution:
def numSquares(self, n):
def is_divided_by(n, count):
"""
return: true if "n" can be decomposed into "count" number of perfect square numbers.
e.g. n=12, count=3: true.
n=12, count=2: false
"""
if count == 1:
return n in square_nums
for k in square_nums:
if is_divided_by(n - k, count - 1):
return True
return False
square_nums = set([i * i for i in range(1, int(n**0.5)+1)])
for count in range(1, n+1):
if is_divided_by(n, count):
return count
思路4:
数学运算。
1770 年,Joseph Louis Lagrange证明了一个定理,称为四平方和定理,也称为 Bachet 猜想,它指出每个自然数都可以表示为四个整数平方和: p = a 0 2 + a 1 2 + a 2 2 + a 3 2 p=a_{0}^{2}+a_{1}^{2}+a_{2}^{2}+a_{3}^{2} p=a02+a12+a22+a32。其中 a 0 a_0 a0到 a 3 a_3 a3为整数。例如,3,31 可以被表示为四平方和如下: 3 = 1 2 + 1 2 + 1 2 + 0 2 31 = 5 2 + 2 2 + 1 2 + 1 2 3=1^{2}+1^{2}+1^{2}+0^{2} \quad 31=5^{2}+2^{2}+1^{2}+1^{2} 3=12+12+12+0231=52+22+12+12。
Adrien Marie Legendre用他的三平方定理完成了四平方定理,证明了正整数可以表示为三个平方和的一个特殊条件: n ≠ 4 k ( 8 m + 7 ) ⟺ n = a 0 2 + a 1 2 + a 2 2 n \neq 4^{k}(8 m+7) \Longleftrightarrow n=a_{0}^{2}+a_{1}^{2}+a_{2}^{2} n=4k(8m+7)⟺n=a02+a12+a22,其中k和m是整数。
结合四平方定理,可以断言,如果这个数不满足三平方定理的条件,它只能分解成四个平方和。
总结一下:
- 1.首先检查数字是否满足四平方定理: n = 4 k ( 8 m + 7 ) n=4^{k}(8 m+7) n=4k(8m+7),如果满足直接返回4。
- 2.判断数字自己是否是完全平方数,或者右两个完全平方数组成(枚举)。
- 3.都不是,只能是3了。
复杂度分析:
时间复杂度: O ( n ) O(\sqrt{n}) O(n),在主循环中,检查数字是否可以分解为两个平方和,这需要 O ( n ) O(\sqrt{n}) O(n)次迭代,其余是在常数时间内解决。
空间复杂度: O ( 1 ) O(1) O(1)
C++:
class Solution {
public:
bool isSuar(int num){
int n = sqrt(num);
return n * n == num;
}
int numSquares(int n) {
while((n & 3) == 0){
n >>= 2;
}
if((n & 7) == 7)
return 4;
if(isSuar(n))
return 1;
for(int i = 1; i < int(sqrt(n))+1; ++i)
if(isSuar(n - i*i))
return 2;
return 3;
}
};
Python:
class Solution:
def isSquare(self, n: int) -> bool:
sq = int(math.sqrt(n))
return sq*sq == n
def numSquares(self, n: int) -> int:
# 四平方和三平方定理
while (n & 3) == 0: # 判断能否被4整除
n >>= 2 # 从number中减去4^k
if (n & 7) == 7: # mod 8 除8 余7的情况,满足四平方定理
return 4
if self.isSquare(n):# 数字本身是个平方数
return 1
# 检查数字是否可以分解成两个平方和 枚举
for i in range(1, int(n**(0.5)) + 1):
if self.isSquare(n - i*i):
return 2
# 只可能是3了
return 3
6.最长上升子序列
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。
进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?
思路:
动态规划。
用数组dp记录答案,即dp[i]表示数组num[0,1,…,i]中最长上升子序列的长度。在计算dp[i]之前,就已经计算了dp[0,1,…,i-1]了。可以得到状态转移方程: d p [ i ] = max ( d p [ j ] ) + 1 , d p[i]=\max (d p[j])+1, dp[i]=max(dp[j])+1, 其中 0 ≤ j < i 0 \leq j0≤j<i 且 num [ j ] < num [ i ] \operatorname{num}[j]<\operatorname{num}[i] num[j]<num[i]。如果不满足条件: num [ j ] < num [ i ] \operatorname{num}[j]<\operatorname{num}[i] num[j]<num[i],则 d p [ i ] = max ( d p [ j ] ) d p[i]=\max (d p[j]) dp[i]=max(dp[j])。最后的答案就是 m a x ( d p [ i ] ) max(dp[i]) max(dp[i])。
复杂度分析:
时间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n为数组nums 的长度。动态规划的状态数为 n,计算dp[i]时,需要遍历dp[0,1,...,i-1],所有总的时间是 O ( n 2 ) O(n^2) O(n2)。
时间复杂度: O ( n ) O(n) O(n),用来存储dp数组。
C++:
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> dp(nums.size(), 0);
if(nums.size() == 0) return 0;
for(int i = 0; i < nums.size(); ++i){
dp[i] = 1;
for(int j = 0; j < i; ++j){
if(nums[i] > nums[j])
dp[i] = max(dp[i], dp[j] + 1);
}
}
return *max_element(dp.begin(), dp.end());
}
};
Python:
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
if not nums:
return 0
dp = []
for i in range(len(nums)):
dp.append(1)
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)
思路2:
贪心 + 二分查找(tql),来自官方题解。
总结一下:
- 1.维护一个数组
d[i],表示长度为i的最长上升子序列的末尾元素值。并使用len记录当前最长上升子序列的长度,初始时,即len=1,d[i]=nums[0]。 - 2.d[i]是关于i单调递增的。官方是用反证法证明的。如果存在 d [ j ] > = d [ i ] d[j]>=d[i] d[j]>=d[i],且满足 j < i jj<i的情况,那么就把长度为i的最长上升子序列末尾截断(长度为i-j),那么剩下的序列长度为j,那么这个序列的最后一个元素为 x x x且必定小于d[i],那么根据条件,也应该小于d[j],也就是找到了一个长度为j的最长上升子序列,但末尾元素却小于d[j]和
d[i],表示长度为i的最长上升子序列的末尾元素值矛盾。 - 3.无序列表证明单调性有两个好处:1.可以使用二分法;2.数组d的长度即为最长子序列的长度;
- 4.整个算法流程可以归纳为:设当前已求出的最长上升子序列的长度为 l e n len len(初始化为1),从前往后遍历数组 n u m s nums nums,在遍历到 n u m s [ i ] nums[i] nums[i]时,:
如果 n u m s [ i ] > d [ l e n ] nums[i]>d[len] nums[i]>d[len],则直接加入到 d d d数组末尾,并更新 l e n = l e n + 1 len = len+1 len=len+1;
否则,在 d d d数组中二分查找,找到一个比 n u m s [ i ] nums[i] nums[i]小的数 d [ k ] d[k] d[k],并更新 d [ k + 1 ] = n u m s [ i ] d[k+1]=nums[i] d[k+1]=nums[i]
C++:
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int len = 1/*初始化*/, n = (int)nums.size();/*数组长度*/
if(n == 0) return 0;
vector<int> d(n + 1, 0);
d[len] = nums[0];
for(int i = 1; i < n; ++i){
if(nums[i] > d[len]) d[++len] = nums[i];
else{
// 如果找不到说明所有的数都比 nums[i] 大,此时要更新 d[1],所以这里将 pos 设为 0
int l = 1, r = len, pos = 0;
while(l <= r){
int mid = (l + r)>>1;
if(d[mid] < nums[i]){
pos = mid;
l = mid + 1;
}
else r = mid - 1;
}
d[pos + 1] = nums[i];
}
}
return len;
}
};
Python:
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
d = [] # dp数组
for n in nums:
if not d or n > d[-1]: # 如果数组为空,或者 num[j] > num[i]时
d.append(n) # 添加元素
else:
l, r = 0, len(d) - 1 # 左 右指针
loc = r
# 二分查找
while l <= r:
mid = (l + r) // 2
if d[mid] >= n:
loc = mid
r = mid - 1
else:
l = mid + 1
d[loc] = n
return len(d)
7.零钱兑换
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:
输入: coins = [2], amount = 3
输出: -1
说明:
你可以认为每种硬币的数量是无限的。
思路:
官方思路:搜索回溯(会超时)
建立模型: min x ∑ i = 0 n − 1 x i \min _{x} \sum_{i=0}^{n-1} x_{i} minx∑i=0n−1xi subject to ∑ i = 0 n − 1 x i ∗ c i = S \sum_{i=0}^{n-1} x_{i} * c_{i}=S ∑i=0n−1xi∗ci=S
其中 S S S是总金额, c i c_i ci是第 i i i枚硬币的面值, x i x_i xi是面值为 c i c_i ci的硬币数量,由于 x i ∗ c i x_i*c_i xi∗ci不能超过总金额 S S S,可以得出 x i x_i xi最多不会超过 S / c i S/c_i S/ci,所以 x i x_i xi的取值范围为 [ 0 , S / c i ] [0, S/c_i] [0,S/ci]。
使用搜索回溯生成满足上述约束条件范围 ( [ 0 , S / c i ] [0, S/c_i] [0,S/ci])内的所有硬币数量子集 [ x 0 , . . . , x n − 1 ] [x_0,...,x_{n-1}] [x0,...,xn−1]。对给定的子集计算它们组成的金额数,如果金额数为 S S S,则记录返回合法硬币总数的最小值,反之返回**-1**。
C++
public class Solution {
public int coinChange(int[] coins, int amount) {
// 调用初始条件
return coinChange(0, coins, amount);
}
// 回溯法三要素:退出条件,回溯过程,递归参数
// 参数为当前用的硬币索引,硬币数组,当前已经产生的数值
private int coinChange(int idxCoin, int[] coins, int amount) {
// 回溯退出
if (amount == 0) return 0;
// 回溯执行的条件,仍然有硬币可用或仍有余额
if (idxCoin < coins.length && amount > 0) {
// 当前值用几个当前硬币表示(向下取整)
int maxVal = amount / coins[idxCoin];
int minCost = Integer.MAX_VALUE;
// 回溯核心内容,每取一个当前硬币,探索其他情况,x为当前用了几个该面值硬币
for (int x = 0; x <= maxVal; x++) {
// 仍有余额,即为 amount - coins[idxCoin] >= 0
if (amount >= x * coins[idxCoin]) {
// 用下一个硬币试试
int res = coinChange(idxCoin + 1, coins, amount - x * coins[idxCoin]);
// 回溯成功,下一种情况也有解
if (res != -1)
// 与目前的最优解比比看
minCost = Math.min(minCost, res + x);
}
}
// 最小代价没有更新,说明所有方案无效
return (minCost == Integer.MAX_VALUE)? -1: minCost;
}
// 没有执行上一个返回那就是一次也没有运行,直接失败
return -1;
}
}
- F ( S ) F(S) F(S):组成金额 S S S所需的最少硬币数量。
- [ c 0 , . . . , c n − 1 ] [c_0,...,c_{n-1}] [c0,...,cn−1]:可选的 n n n枚硬币面额值。
假设知道 F ( S ) F(S) F(S),和最后一枚硬币的面值是 C C C 。那么由于问题的最优子结构,转移方程为: F ( S ) = F ( S − C ) + 1 F(S)=F(S-C)+1 F(S)=F(S−C)+1
C C C是不确定的,需要枚举 c 0 , . . . , c n − 1 c_0,...,c_{n-1} c0,...,cn−1,并选择其中的最小值。下列递推关系成立:
F ( S ) = min i = 0... n − 1 F ( S − c i ) + 1 F(S)=\min _{i=0 . . . n-1} F\left(S-c_{i}\right)+1 F(S)=mini=0...n−1F(S−ci)+1 subject to S − c i ≥ 0 S-c_{i} \geq 0 S−ci≥0
F ( S ) = 0 , F(S)=0, F(S)=0, when S = 0 S=0 S=0
F ( S ) = − 1 , F(S)=-1, F(S)=−1, when n = 0 n=0 n=0
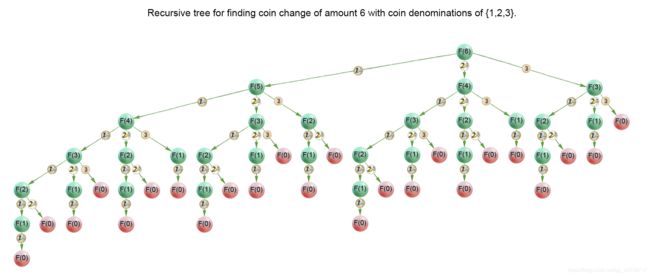
为了避免重复的计算,我们将每个子问题的答案存在一个数组中进行记忆化,如果下次还要计算这个问题的值直接从数组中取出返回即可,这样能保证每个子问题最多只被计算一次。
复杂度分析:
时间复杂度: O ( S n ) O(Sn) O(Sn), 其中 S S S是金额, n n n 是面额数。我们一共需要计算 S S S个状态的答案,且每个状态 F ( S ) F(S) F(S)由于上面的记忆化的措施只计算了一次,而计算一个状态的答案需要枚举 n n n个面额值,所以一共需要 O ( S n ) O(Sn) O(Sn)的时间复杂
度。
空间复杂度: O ( S ) O(S) O(S), 我们需要额外开一个长为 S S S的数组来存储计算出来的答案 F ( S ) F(S) F(S).
C++
class Solution {
vector<int> count; // 存储中间计算结果,空间换时间, 避免重复计算
public:
int coinChange(vector<int>& coins, int amount) {
if(amount < 1) return 0; // 初始条件检查
count = vector<int>(amount, 0); //初始化
return coinChangeCore(coins, amount); // 动态规划入口
}
int coinChangeCore(vector<int>& coins, int rem){
if(rem < 0) return -1; // 结束条件:此路径不通
if(rem == 0) return 0; // 结束条件:余额为0,成功结束
if(count[rem - 1] !=0) return count[rem - 1];// 直接返回结果,避免重复计算
int Min = INT_MAX; // 极大值
for(auto coin : coins){
// 用一下coin这个面值的硬币会怎样?res是这个方法的最优情况
int res = coinChangeCore(coins, rem - coin);
if(res >= 0 && res <Min ){ // res < 0说明此路不同
Min = res + 1; // 更新Min
}
}
// count[rem - 1]存储着给定金额amount的解
// 若为INT_MAX则该情况无解
count[rem - 1] = Min == INT_MAX ? -1 : Min;
return count[rem - 1];
}
};
Python:
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
# 先判断
if amount < 1:
return 0
self.count = [0] * amount
return self.coinChangeCore(coins, amount)
def coinChangeCore(self, coins, rem): # 硬币金额、 余额
if rem < 0:
return -1
if rem == 0:
return 0
if self.count[rem -1] != 0:
return self.count[rem -1]
Min = float("inf")
for coin in coins:
res = self.coinChangeCore(coins, rem - coin)
if res >= 0 and res < Min:
Min = res + 1
self.count[rem - 1] = Min if Min < float("inf") else -1
return self.count[rem - 1]
思路3:
官方思路:动态规划-自下而上
仍然定义 F ( i ) F(i) F(i):组成金额 i i i所需的最少硬币数量。假设在计算 F ( i ) F(i) F(i)之前,已经计算出 F ( 0 ) F(0) F(0)到 F ( i − 1 ) F(i-1) F(i−1)的答案,则对应的转移方程为:
F ( i ) = min j = 0 … n − 1 F ( i − c j ) + 1 F(i)=\min _{j=0 \ldots n-1} F\left(i-c_{j}\right)+1 F(i)=minj=0…n−1F(i−cj)+1
中 c j c_j cj代表的是第j枚硬币的面值,即我们枚举最后一枚硬币面额是 c j c_j cj,那么需要从 i − c j i-c_j i−cj这个金额的状态 F ( i − c j ) F(i- c_j) F(i−cj)转移过来,再算上枚举的这枚硬币数量1的贡献,由于要硬币数量最少,所以F(i)为前面能转移过来的状态的最小值加上枚举的硬币数量1。
给出官方给的两个例子理解:


复杂度分析
●时间复杂度: O ( S n ) O(Sn) O(Sn),其中 S S S是金额, n n n是面额数。我们一共需要计算 O ( S ) O(S) O(S)个状态, S S S为题目所给的总金额。对于每个状态,每次需要枚举 n n n个面额来转移状态,所以一共需要 O ( S n ) O(Sn) O(Sn)的时间复杂度。
●空间复杂度: O ( S ) O(S) O(S)。DP数组需要开长度为总金额 S S S的空间。
C++:
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int Max = amount + 1;
vector<int> dp(amount + 1, Max);
dp[0] = 0; // 初始化第一个
for(int i = 1; i <= amount; ++i){// 金额从1开始
for(int j = 0; j < coins.size(); ++j){
if(coins[j] <= i){// 当硬币小于等于
// 转移方程: F(i) = min F(i - cj) + 1
dp[i] = min(dp[i], dp[i - coins[j]] + 1);
}
}
}
// 如果不存在 则 dp[amount]=Max=amount + 1 > amount
return dp[amount] > amount ? -1 : dp[amount];
}
};
Python:
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
Max = amount + 1
dp = [Max] * (amount + 1)
dp[0] = 0
for i in range(1, amount +1):
for coin in coins:
if coin <= i:# 只有硬币金额小于等于 amount 才有解
dp[i] = min(dp[i], dp[i - coin] + 1)
return dp[amount] if dp[amount] < Max else -1
8.矩阵中的最长递增路径
给定一个整数矩阵,找出最长递增路径的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你不能在对角线方向上移动或移动到边界外(即不允许环绕)。
示例 1:
输入: nums =
[
[9,9,4],
[6,6,8],
[2,1,1]
]
输出: 4
解释: 最长递增路径为 [1, 2, 6, 9]。
思路:
朴素的深度优先搜索,超时。
深度优先搜索可以找到从任何单元格开始的最长递增路径。可以对全部单元格进行深度优先搜索。
每个单元格可以看作图 G G G中的一个定点。若两相邻细胞的值满足 a < b a < b a<b,则存在有向边 ( a , b ) (a, b) (a,b)。问题转化成:
寻找有向图 G G G中的最长路径。可以使用集合visited 来避免重复访问,但是这里不用 visited 的原因是,找的是升序的路径,所以进来了就不会再返回,用 visited 没有意义。
复杂度分析:
时间复杂度: O ( 2 m + n ) O(2^{m+n}) O(2m+n)。对每个有效递增路径均进行搜索。在最坏情况下,会有 O ( 2 m + n ) O(2^{m+n}) O(2m+n)次调用。
空间复杂度: O ( m n ) O(mn) O(mn)。对于每次深度优先搜索,系统栈需要 O ( h ) O(h) O(h)空间,其中 h h h为递归的最深深度。最坏情况下 O ( h ) = O ( m n ) O(h)=O(mn) O(h)=O(mn)
C++
class Solution {
public:
int row, col;
// 移动的四个方向
vector<vector<int>> dirs{ {0,1}, {1,0}, {0,-1},{-1,0} };
int longestIncreasingPath(vector<vector<int>>& matrix) {
if (matrix.size() == 0) return 0;
row = matrix.size();
col = matrix[0].size();
int res = 0;
for (int i = 0; i < row; ++i)
for (int j = 0; j < col; ++j)// 以i,j出发
res = max(res, dfs(matrix, i, j));// 深度遍历
return res;
}
int dfs(vector<vector<int>>& matrix, int i, int j) {
int res = 0;
for (auto dir : dirs) {// 四个方向
int y = i + dir[0], x = j + dir[1];// 偏移后的坐标
if (0 <= x && x < col && 0 <= y && y < row && matrix[y][x] > matrix[i][j]) {
// 如果在范围内,且满足比上一条路径大
res = max(res, dfs(matrix, y, x));
}
}
// 边界条件,无路可走或者找不到更大的值
return ++res;
}
};
Pyrhon:
class Solution:
def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
if len(matrix) == 0:
return 0
self.row = len(matrix)
self.col = len(matrix[0])
self.dirs = [[0,1], [1,0], [0,-1], [-1,0]]
res = 0
for i in range(self.row):
for j in range(self.col):
res = max(res, self.dfs(matrix, i, j))
return res
def dfs(self, matrix, i, j):
res = 0
for dir in self.dirs:
y = i + dir[0]
x = j + dir[1]
if y >= 0 and y < self.row and x >= 0 and x < self.col \
and matrix[y][x] > matrix[i][j]:
res = max(res, self.dfs(matrix, y, x))
res += 1
return res
思路2:
记忆化深度优先搜索
将递归的结果存储下来,这样每个子问题只需要计算一次。
一个优化途径是我们可以用一个集合来避免一次深度优先搜索中的重复访问。该优化可以将一次深度优先搜索的时间复杂度优化到 O ( m n ) O(mn) O(mn),总时间复杂度 O ( m 2 n 2 ) O(m^2n^2) O(m2n2)。
在计算中,记忆化是一种优化技术,它通过存储“昂贵”的函数调用的结果,在相同的输入再次出现时返回缓存的结果,以此加快程序的速度。
在本题中,多次调用dfs,但是如果知道了相邻四格的计算结果,就只需要花常数时间获取,如果没有,则在搜索的过程中保存。
复杂度分析:
时间复杂度: O ( m n ) O(mn) O(mn)。 每个顶点/单元格均计算一次,且只被计算一次。每条边也均计算一次并只计算一次。总时间复杂度是 O ( V + E ) O(V+E) O(V+E)。其中 V V V是顶点总数, E E E是边总数。本问题中 O ( V ) = O ( m n ) O(V)=O(mn) O(V)=O(mn), O ( E ) = O ( 4 V ) = O ( m n ) O(E)=O(4V)=O(mn) O(E)=O(4V)=O(mn)。
C++:
class Solution {
public:
int row, col;
// 移动的四个方向
vector<vector<int>> dirs{ {0,1}, {1,0}, {0,-1},{-1,0} };
int longestIncreasingPath(vector<vector<int>>& matrix) {
if (matrix.size() == 0) return 0;
row = matrix.size();
col = matrix[0].size();
// 定义大小
vector<vector<int>> cache(row, vector<int>(col, 0));
int res = 0;
for (int i = 0; i < row; ++i)
for (int j = 0; j < col; ++j)// 以i,j出发
res = max(res, dfs(matrix, i, j, cache));// 深度遍历
return res;
}
int dfs(vector<vector<int>>& matrix, int i, int j,vector<vector<int>>& cache) {
if (cache[i][j] != 0) return cache[i][j];
for (auto dir : dirs) {// 四个方向
int y = i + dir[0], x = j + dir[1];// 偏移后的坐标
if (0 <= x && x < col && 0 <= y && y < row && matrix[y][x] > matrix[i][j]) {
// 如果在范围内,且满足比上一条路径大
cache[i][j] = max(cache[i][j], dfs(matrix, y, x, cache));
}
}
// 边界条件,无路可走或者找不到更大的值
return ++cache[i][j];
}
};
Python:
class Solution:
def longestIncreasingPath(self, matrix):
if len(matrix) == 0:
return 0
self.row = len(matrix)
self.col = len(matrix[0])
self.dirs = [[0,1], [1,0], [0,-1], [-1,0]]
# !!!注意必须用下面的方式创建二维list
self.cache = [[0 for i in range(self.col)] for j in range(self.row )]
res = 0
for i in range(self.row):
for j in range(self.col):
res = max(res, self.dfs(matrix, i, j))
return res
def dfs(self, matrix, i, j):
if self.cache[i][j] != 0:
return self.cache[i][j]
for dir in self.dirs:
y = i + dir[0]
x = j + dir[1]
if y >= 0 and y < self.row and x >= 0 and x < self.col \
and matrix[y][x] > matrix[i][j]:
self.cache[i][j] = max(self.cache[i][j], self.dfs(matrix, y, x))
self.cache[i][j] += 1
return self.cache[i][j]
