力扣每日一题 Day 3（螺旋矩阵）

题目描述

给你一个 m 行 n 列的矩阵 matrix ，请按照顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：
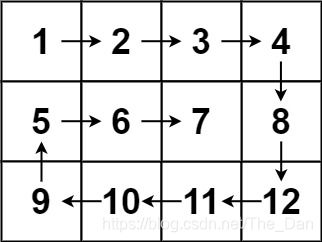
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：
m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

来源：力扣（LeetCode）
链接: https://leetcode-cn.com/problems/spiral-matrix/.

题解思路

按矩阵划分，每个矩阵按照顺时针添加到向量里。所以外层为一层循环，内层为4个循环，分别对应上右下左。

一开始示例一很快就能通过，但示例二出现runtime error错误。查询题解时发现某位大佬的思路与我本质上是相同的，但他的外层循环是到（min(high,size)-1)/2，我是到(high-1)就结束了。这里卡住了好久，最后才想明白，矩阵的个数只跟长宽中较小的那个有关。

还有一个参考了的点在于内层循环的第三个循环和第四个循环，(high-1-i != i)和(size-1-i != i)，确实没有考虑完全只有一行或一列的情况。
总的来说，这应该是运行速度比较快的一种思路了。只是占用的内存确实还是有待改进。

代码部分

class Solution {
public:
    vector spiralOrder(vector>& matrix) {
        vectorvec;
        int i, j, k, l ,n;
        int high = matrix.size();
        int size = matrix[0].size();
        for(i = 0;i <= (min(high,size)-1)/2; i++){
            for(j = i; j <= size-i-1; j++)
                vec.push_back(matrix[i][j]);
            for(k = i+1; k < high-i; k++)
                vec.push_back(matrix[k][size-i-1]);
            for(l = size-i-2; l >= i && (high-1-i != i); l--)
                vec.push_back(matrix[high-i-1][l]);
            for(n = high-i-2; n > i && (size-1-i != i); n--)
                vec.push_back(matrix[n][i]);
        }
        return vec;
    }
};

小结

思考问题还是不够全面，没能考虑到一些特殊情况，对于题目的理解还需要更加强一点。