动态规划——背包问题

01背包

解题思路：动态规划
将状态方程从前往后一直推到最终答案状态

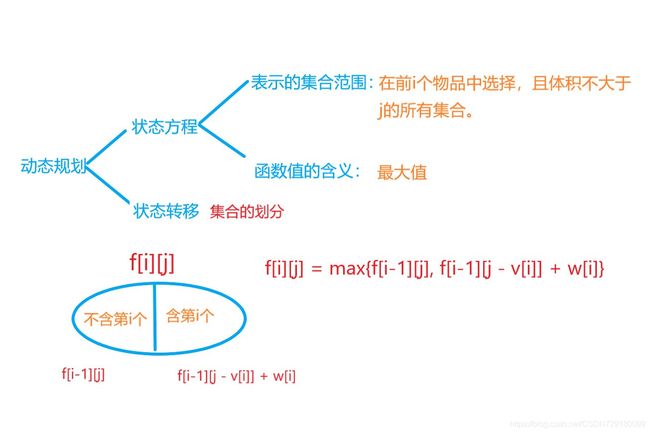
由动态方程可以看出，后一个状态可以由前一个状态推出，所以可以递推出f[n][v] 即在前n个物品中选择体积不超过v的集合中权值最大值是多少。

例题：01背包问题
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 v_i，价值是 w_i。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 v_i,w_i，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0 0i,w_i≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例：
8

优化前代码：

#include
#include

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
	cin >> n >> m;
	for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
	// 从前往后递推到n
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++)
		{
			f[i][j] = f[i-1][j];
			if(j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]); // 状态转移方程，当背包当前容量大于等于v[i]时递推。
		}
		cout << f[n][m];

		return 0;
}	

优化：从物理存储的角度进行优化，因为二维数组每一行的计算只用到前一行的数值。所以可以优化为滚动数组，用后面的值覆盖前面的值。

优化后代码：

#include
#include

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
	cin >> n >> m;
	for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
	for(int i = 1; i <= n; i++)
		for(int j = m; j >= v[i]; j--)
		{
			f[j] = max(f[j], f[j-v[i]] + w[i]); // 由于j-v[i]
		}
	cout << f[n][m] << endl;

	return 0;
}	

完全背包

动态规划图解

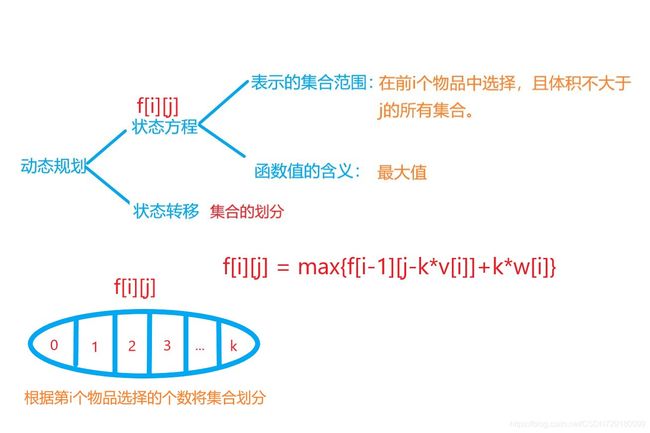
例题：完全背包问题
有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是 v_i，价值是 w_i。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行两个整数 v_i,w_i，用空格隔开，分别表示第 i 种物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0 0i,w_i≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例：
10

原始递推代码

#include
#include

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N]; //v[N]中存体积，w[N]中存权值
int f[N][N];

int main()
{
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
	
	for(int i = 1; i <= n; i++)
		for(int j = 0; j <= m; j++)
			for(int k = 0; k * v[i] < j; k++)
				f[i][j] = max(f[i][j], f[i-1][j - v[i] * k] + k * w[i]);
	
	cout << f[n][m] << endl;
	return 0;
}	

优化

#include
#include

using namespace std;

const int N =1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
	
	for(int i = 1; i <= n; i++)
		for(int j = 0; j <= m; j++)
		{
			f[i][j] = f[i-1][j];
			if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j-v[i]]+w[i]);
		}
	cout << f[n][m] << endl;
	return 0;
}		

与01背包相同的物理存储优化为滚动数组

#include
#include

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
	
	for(int i = 1; i <= n; i++)
		for(int j = v[i]; j <= m; j++)
			f[j] =  max(f[j], f[j-v[i]] + w[i]);
	cout << f[m] << endl;
	return 0;
}			

多重背包

当问题规模较小时，可以类似于完全背包问题加多加了一个限制条件 k <= s[i]， 如例题1
当问题规模交到是时，优化利用打包原理巧妙的将问题转化为01背包问题， 如例题2

例题1：多重背包问题I
有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 v_i，价值是 w_i。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行三个整数 v_i,w_i,s_i，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式
输出一个整数，表示最大价值。

数据范围
0 0i,w_i,s_i≤100
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例：
10

#include
#include

using namespace std;

const int N = 110;

int n, m; 
int v[N], w[N], s[N];
int f[N][N];

int main()
{
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
	
	for(int i = 1; i <= n; i++)
		for(int j = 0; j <= m; j++)
			for(int k = 0; k*v[i] <= j && k <= s[i]; k++)
				f[i][j] = max(f[i][j], f[i-1][j - k*v[i]] + k*w[i]);
	cout << f[n][m] << endl;
	return 0;
}

例题2：多重背包问题II
有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 s_i 件，每件体积是 v_i，价值是 w_i。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行三个整数 v_i,w_i,s_i，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式
输出一个整数，表示最大价值。

数据范围
0 0 0i,w_i,s_i≤2000
提示：
本题考查多重背包的二进制优化方法。

输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例：
10

#include
#include

using namespace std;

const int N = 25000; //由于分组后共有N * logs个状态所以开25000

int n, m;
int v[N], w[N];
int f[N];

int main()
{	 
	cin >> n >> m;
	
	int cnt = 0;
	for(int i = 1; i <= n; i++)
	{
		int a, b, c;
		cin >> a >> b >> s;
		int k = 1;
		//将每一组同类物品打包，即把他化成以一个等比数列（公比为2）+C的形式
		while (k <= s)
		{
			cnt++;
			v[cnt] = a * k;
			w[cnt] = b * k;
			s -= k;
			k *= 2;
		}
		if(s > 0) // 计算余项C
		{
			cnt ++;
			v[cnt] = a * s;
			w[cnt] = b * s;
		}
	}
	n = cnt;
	
	//把整个数组看成01背包问题求解
	for(int i = 1; i <= n; i ++)
		for(int j = m; j >= v[i]; j--)
			f[j] = max(fj], f[j-v[i]] + w[i]);
	cout << f[m] << endl;
	return 0;
}	

分组背包

与完全背包问题相类似，这里是从第i组中挑第几个的问题，所以类似于完全背包
状态方程为f[i][j] = max(f[i][j], f[i-1][j-v[i][k]] + w[i][k])

例题：分组背包问题
有 N 组物品和一个容量是 V 的背包。

每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 v_ij，价值是 w_ij，其中 i 是组号，j 是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式
第一行有两个整数 N，V，用空格隔开，分别表示物品组数和背包容量。

接下来有 N 组数据：

每组数据第一行有一个整数 Si，表示第 i 个物品组的物品数量；
每组数据接下来有 Si 行，每行有两个整数 v_ij,w_ij，用空格隔开，分别表示第 i 个物品组的第 j 个物品的体积和价值；
输出格式
输出一个整数，表示最大价值。

数据范围
0 0 0ij,w_ij≤100
输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例：
8

#include
#include

using namespace std;

const int N = 110;

int n, m;
int v[N][N], w[N][N], s[N];
int f[N];

int main()
{
    cin >> n >> m;
    
    for(int i = 1; i <= n; i++)
    {
        cin >> s[i];
        for(int j = 1; j <= s[i]; j++)
            cin >> v[i][j] >> w[i][j];
    }
    
    for(int i = 1; i <= n; i++)
        for(int j = m; j >= 0; j--)
            for(int k = 1; k <= s[i]; k++)
                if(j >= v[i][k]) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
                
    cout << f[m] << endl;
    return 0;
}