计算机视觉——模型分析
文章目录
-
- 一、模型可视化分析
-
- 1. 结构可视化
-
- 1.1 Netron工具
- 1.2 Graphviz工具
- 2. 权重可视化
- 3. 反卷积篇
-
- 3.1 反卷积可视化原理
- 3.2 反卷积可视化使用
- 4. 激活热图
-
- 4.1 CAM模型
- 4.2 GradCAM模型
- 二、模型复杂度分析
-
-
- 1. 理论复杂度分析
-
- 1.1 FLOPs计算
- 1.2 MAC计算
- 2. 复杂度分析工具
-
- 2.1 trochsummary工具
- 2.2 torchstat工具
-
- 三、模型速度分析
-
-
- 1. profiler工具
- 2. Profiler TensorBoard插件
-
一、模型可视化分析
1. 结构可视化
1.1 Netron工具
-
可以查看网络拓扑结构与卷积核尺寸、权重等
-
Netron支持的格式:支持ONNX,TensorFlow Lite, Keras,Caffe,Darknet,ncnn,MNN,PaddlePaddle,Core ML,MXNet,RKNN,MindSpore Lite,TNN,Barracuda,Tengine,TensorFlow.js,Caffe2 and UFF
-
部分支持PyTorch,TensorFlow,TorchScript,OpenVINO Torch,Vitis Al,Arm NN,BigDL,Chainer,CNTK,
Deeplearning4j,MediaPipe,MLNET and scikit-learn -
使用:
- 网页版:https://netron.app/
- 本地版:https://github.com/lutzroeder/netron
-
ONNX格式(Open Neural Network Exchange):ONNX是一种针对机器学习所设计的开放式的文件格式,用于存储训练好的模型。它使得不同的人工智能框架(如Pytorch,MXNet)可以采用相同格式存储模型数据并交互。
-
Pytorch ONNX格式导出
torch.onnx.export(mynet,dummy_input,"model.onnx",verbose=False) # mynet 是神经网络模型,dummuy_input是输入,取名为"model.onnx", verbose 用于控制是否在控制台上输出额外的信息,例如正在转换哪些节点以及转换进度等

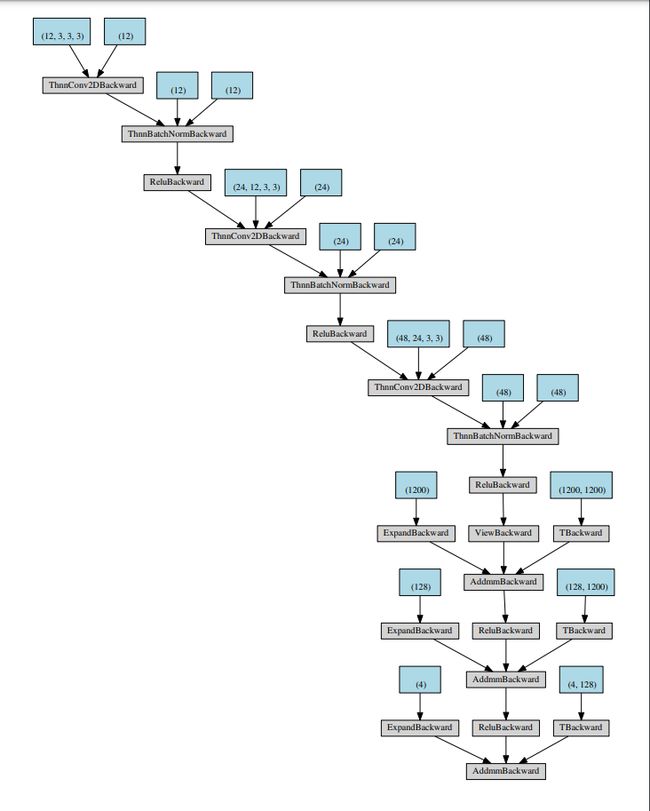
1.2 Graphviz工具
通用绘图工具(Graph Visualization Software的缩写)是一个由AT&T实验室启动的开源工具包,用于绘制DOT语言脚本描述的图形。
- 生成神经网络模型图
from graphviz import Digraph
from torch.autograd import Variable
def make_dot(var, params=None):
if params is not None:
assert isinstance(params.values()[0], Variable)
param_map = {id(v): k for k, v in params.items()}
# 设置属性(填充颜色、形状、对齐方式、字体大小、最小垂直距离、高度)
node_attr = dict(style='filled',
shape='box',
align='left',
fontsize='12',
ranksep='0.1',
height='0.2')
# 创建图
dot = Digraph(node_attr=node_attr, graph_attr=dict(size="12,12"))
seen = set()
def size_to_str(size): # 将张量大小转换为字符串,并将其添加到节点名称中,以便更好地显示张量的信息
return '('+(', ').join(['%d' % v for v in size])+')'
#添加节点
#Tensor类型的节点将显示为一个橙色的矩形,Variable类型的节点将显示为一个浅蓝色的矩形,参数(如权重和偏差)则显示为绿色矩形。对于Variable类型的节点,节点标签将包括它的名称和形状。
def add_nodes(var):
if var not in seen:
if torch.is_tensor(var):
dot.node(str(id(var)), size_to_str(var.size()), fillcolor='orange')
elif hasattr(var, 'variable'):
u = var.variable
name = param_map[id(u)] if params is not None else ''
node_name = '%s\n %s' % (name, size_to_str(u.size()))
dot.node(str(id(var)), node_name, fillcolor='lightblue')
else:
dot.node(str(id(var)), str(type(var).__name__))
seen.add(var)
if hasattr(var, 'next_functions'):
for u in var.next_functions:
if u[0] is not None:
dot.edge(str(id(u[0])), str(id(var)))
add_nodes(u[0])
if hasattr(var, 'saved_tensors'):
for t in var.saved_tensors:
dot.edge(str(id(t)), str(id(var)))
add_nodes(t)
add_nodes(var.grad_fn)
return dot
- 工具 torchviz 封装好了 make_dot 函数
- pip install torchviz
- from torchviz import make_dot
2. 权重可视化
import torch
import numpy as np
import matplotlib.pyplot as plt
# 定义一个函数用于可视化卷积层
def visualize_layer(layer, nrow=4, padding=2):
# 获取卷积层的权重
weight = layer.weight.data.clone()
cout, cin, h, w = weight.shape
# 将每个卷积核的权重分别拼接在一起
weight = weight.view(cout*cin, 1, h, w)
weight_grid = make_grid(weight, normalize=True, scale_each=True, nrow=nrow, padding=padding)
# 将图像转化为numpy数组
weight_np = weight_grid.numpy().transpose((1, 2, 0)) #CHW->HWC
# 绘制图像
plt.imshow(weight_np)
# 实例化模型
model = simpleconv3(nclass)
# 获取第一个卷积层
conv1_layer = model.conv1
# 可视化第一个卷积层每个卷积核
visualize_layer(conv1_layer)
# 显示图像
plt.show()
3. 反卷积篇
ZFNet:通过引入更小的卷积核和更深的网络结构来提高性能,还使用了反卷积技术对网络的中间特征层进行可视化。
3.1 反卷积可视化原理
-
反卷积操作原理
前向传播时记录下最大池化的位置,反向池化时就是通过记录的位置进行上采样,激活函数依旧使用ReLU。
对于步长不为1的卷积,反向计算时,使用转置卷积(与前向的卷积核共用)进行反向传播。

-
可视化流程:
- 首先,选取需要可视化的卷积层,获取该卷积层的输出特征图。
- 对于选取的卷积层,将其输出特征图经过上采样操作,将特征图的大小扩大到原始图像的大小。
- 然后,将上采样后的特征图与原始图像进行叠加,得到一个新的图像。
- 将得到的新图像输入到卷积神经网络中,通过反向传播计算梯度,最终得到反卷积的权重。
- 利用反卷积权重对卷积层的输出特征图进行反卷积操作,得到对应于原始图像的反卷积特征图。
- 最后,将反卷积特征图进行可视化,可以得到对应卷积层的视觉解释。
-
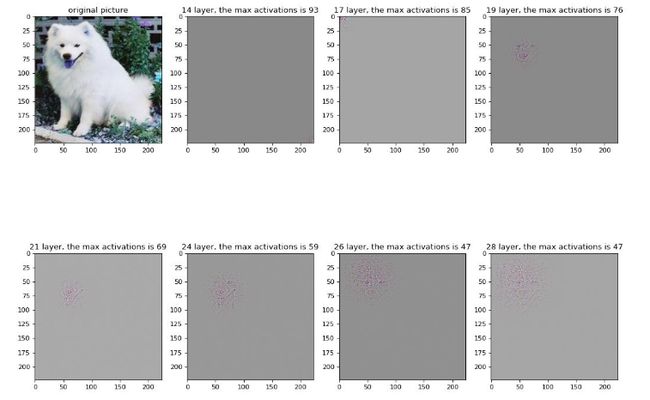
反卷积可视化的实验结果:
- 层数越高,特征图越能反应出原图的轮廓,越具有良好的不变性。说明模型越到深层越能学到更加抽象的特征。
2. 低层特征快速收敛,高层特征收敛更慢。
3. 平移和尺度缩放:随着幅度线性增加,高层比低层变换幅度低,预测概率相对稳定,说明高层越具有平移不变性。
4. 旋转:低层和高层变化幅度大,预测概率很不稳定。
3.2 反卷积可视化使用
4. 激活热图
4.1 CAM模型
-
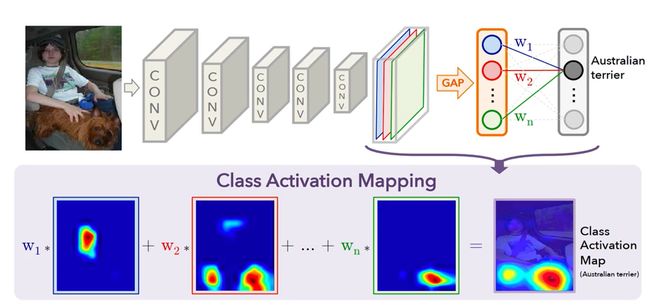
Class Activation Map:类激活映射热图
查看输出的特定类别概率的大小与输入图片中哪些区域的像素值更相关,用于可视化模型学习到的信息。用于可视化模型是否能定位到图片分类中图片真正重要的区域。CAM 可以帮助我们理解神经网络是如何对输入进行分类的,通过将特征图中每个位置的重要性与分类结果相结合,生成一个可视化的结果,即激活热图。
-
基本原理:
一个典型的 CNN 网络的结构是这样的:先通过一系列的“卷积+激活+下采样”单元,将输入图片的特征图逐渐缩小并提取各个尺度上的特征,然后使用一个全局平均池化层(GAP)将二维的特征图降到一维,最后再接一个输出维度为分类类别数的全连接层,以输出各个类别的最终输出权重,权重最高的类别即为模型的判别结果。这个过程中 GAP 层将最后一个卷积层提取的特征图从二维降到了一维,失去了空间特征信息。如果将最后一个卷积层输出的二维特征图不经过 GAP 层直接与最后的全连接层的权重w相乘,即能保留二维特征图的二维空间特性,又能反应特征图对当前分类输出的重要性。
-
CAM 的实现过程如下:
- 通过卷积神经网络将输入图像转换为特征图;
- 对于最后一个卷积层的特征图,应用全局平均池化,将其压缩为一个特征向量;
- 将这个特征向量通过一个权重矩阵进行加权,得到每个特征图位置的类别激活值;
- 将类别激活值进行双线性插值,得到与输入图像大小相同的热力图,表示每个位置对分类结果的贡献。
4.2 GradCAM模型
-
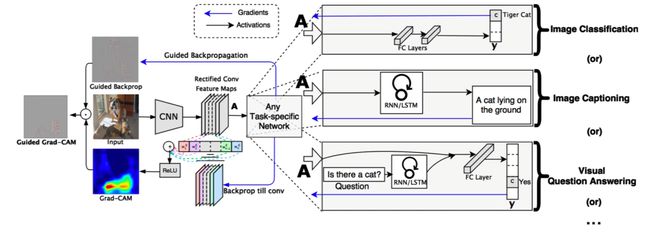
Gradient-weighted Class Activation Mapping:梯度加权类激活映射
CAM的局限性是CAM 的计算依赖“GAP + Softmax 输出分类权重”这个特殊结构,Grad-CAM 使用梯度代替了 CAM 中 GAP 后全连接层的权重参数来给激活图加权。
- Grad-CAM论文原文:https://arxiv.org/abs/1610.02391
- 代码:https://github.com/ramprs/grad-cam/
- 代码解释:https://aistudio.baidu.com/aistudio/projectdetail/1649110
结果展示:
原图:
叠加Grad-CAM:
二、模型复杂度分析
1. 理论复杂度分析
- 常见模型复杂度指标
- FLOPs(floating point operations per Second,浮点操作数)
- MAC(Memory access cost,内存访问代价)
1.1 FLOPs计算
FLOPs的计算方法取决于模型中使用的层类型。
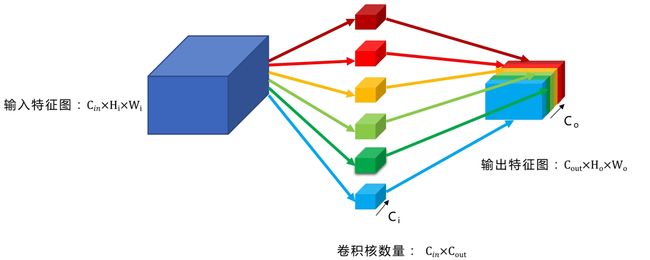
- 多通道卷积的计算量
- 卷积乘法操作数:
c o n v M = C o u t × H o u t × W o u t × C i n × k h × k w conv_{M}=C_{out} \times H_{out} \times W_{out} \times C_{in} \times k_h \times k_w convM=Cout×Hout×Wout×Cin×kh×kw
C表示数据的通道数,k_h 和 k_w 表示卷积核或池化核的高度和宽度。
2. 卷积加法操作数:
c o n v A d d = C o u t × H o u t × W o u t × ( C i n × k h × k w − 1 ) n 个数相加,要加 n − 1 次 conv_{Add}=C_{out} \times H_{out} \times W_{out} \times (C_{in} \times k_h \times k_w-1)\quad n 个数相加,要加n-1次 convAdd=Cout×Hout×Wout×(Cin×kh×kw−1)n个数相加,要加n−1次
3. 偏执加法操作数:
c o n v b i a s = C o u t × H o u t × W o u t conv_{bias}=C_{out}\times H_{out}\times W_{out} convbias=Cout×Hout×Wout
4. 总操作数:
C o u t × H o u t × W o u t × C i n × k h × k w 次乘法与加法,一共 2 × C o u t × H o u t × W o u t × C i n × k h × k w M a d d = c o n v M + c o n v A d d + c o n v b i a s C_{out} \times H_{out}\times W_{out} \times C_{in}\times k_h\times k_w 次乘法与加法,一共2\times C_{out}\times H_{out}\times W_{out}\times C_{in}\times k_h \times k_w\\ \\ \boxed{Madd=conv_{M}+conv_{Add}+conv_{bias}} Cout×Hout×Wout×Cin×kh×kw次乘法与加法,一共2×Cout×Hout×Wout×Cin×kh×kwMadd=convM+convAdd+convbias
卷积FLOPs:
F L O P S c o n v = c o n v M + c o n v b i a s \boxed{FLOP_{S_{conv}}=conv_{M}+conv_{bias}} FLOPSconv=convM+convbias
- 全连接层的计算量:
P L O P s = I u p u t × O u t p u t I n p u t 、 O u t p u t 为输入、输出神经元 M a d d = ( I n p u t + I n p u t − 1 ) × O u t p u t + b i a s b i a s 为偏置 \boxed{PLOPs=Iuput\times Output}\quad Input、Output为输入、输出神经元\\ \\ \boxed{Madd = (Input+Input-1)\times Output+bias} \quad bias为偏置 PLOPs=Iuput×OutputInput、Output为输入、输出神经元Madd=(Input+Input−1)×Output+biasbias为偏置
1.2 MAC计算
内存访问代价(Memory Access Cost)是指执行一次内存访问所需的时间和资源成本。在深度学习中,计算内存访问代价通常需要考虑输入、权重和输出数据的内存访问。卷积神经网络中,每次执行卷积操作时,需要访问输入特征图、权重和输出特征图。
-
输入特征图的访问代价:
C in × H in × W in C_{\text{in}} \times H_{\text{in}} \times W_{\text{in}} Cin×Hin×Win -
权重的访问代价:
C in × C out × k h × k w + C out C_{\text{in}} \times C_{\text{out}} \times k_h \times k_w + C_{\text{out}} Cin×Cout×kh×kw+Cout -
输出特征图的访问代价:
C out × H out × W out C_{\text{out}} \times H_{\text{out}} \times W_{\text{out}} Cout×Hout×Wout
实际的内存访问代价可能会受到许多因素的影响,例如缓存大小、缓存命中率、内存带宽、延迟等。因此,在计算内存访问代价时,需要考虑具体的硬件和实现细节。
2. 复杂度分析工具
- 工具:torchsummary 与 torchstat
- 安装:
pip install torchsummary;pip install torchstat
先定义一个网络模型:
import torch.nn as nn
import torch.nn.functional as F
# 包含3个卷积层,3个BN层,5个ReLU层,3个全连接层。
class simpleconv3(nn.Module):
def __init__(self,nclass):
super(simpleconv3,self).__init__()
self.conv1 = nn.Conv2d(3,12,3,2)
self.bn1 = nn.BatchNorm2d(12)
self.conv2 = nn.Conv2d(12,24,3,2)
self.bn2 = nn.BatchNorm2d(24)
self.conv3 = nn.Conv2d(24,48,3,2)
self.bn3 = nn.BatchNorm2d(48)
self.fc1 = nn.Linear(48*5*5, 1200)
self.fc2 = nn.Linear(1200,128)
self.fc3 = nn.Linear(128,nclass)
def forward(self, x):
x = F.relu(self.bn1(self.conv1(x)))
x = F.relu(self.bn2(self.conv2(x)))
x = F.relu(self.bn3(self.conv3(x)))
x = x.view(-1,48*5*5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
2.1 trochsummary工具
- 可以对每一层的参数量、输入输出形状、fp/bp一次需要的内存大小进行统计(https://github.com/sksq96/pytorch-summary)
使用代码:
from torchsummary import summary
#判断是否有可用的 GPU,如果有模型移动到 GPU 上,否则移动到 CPU 上
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
net = simpleconv3(2).to(device)
# 转换输入张量的类型
inputs = torch.randn(1, 3, 48, 48).to(device)
summary(net,input_size=(3,48,48)) # 输入网络模型和输入张量的形状,这里的input_size不包括批次大小(batch size),批次大小会被默认设置为 1
2.2 torchstat工具
- 可以对每一层的参数量、输入输出形状、计算量进行统计(https://github.com/Swall0w/torchstat)
使用代码:
from torchstat import stat
net = simpleconv3(4)
stat(net,(3,48,48))
注意:如果这里报错AttributeError: module 'numpy' has no attribute 'long',需要将numpy版本重装为1.23.0
pip install numpy==1.23.0
conv1的复杂度计算:
KaTeX parse error: Expected 'EOF', got '&' at position 2: &̲Madd = (12\time…
fc2的复杂度计算:
F L O P s = 1200 × 128 = 153600 M a d d = ( 1200 + 1200 − 1 ) × 128 + 0 = 307072 FLOPs=1200 \times 128 = 153600\\ Madd = (1200+1200-1)\times 128 + 0 = 307072 FLOPs=1200×128=153600Madd=(1200+1200−1)×128+0=307072
三、模型速度分析
1. profiler工具
- pytorch框架自带的性能分析工具,可分析速度、内存等
torch.profiler.profile(*, activities=None, schedule=None, on_trace_ready=None, record_shapes=False, profile_memory=False, with_stack=False, with_flops=False, with_modules=False, use_cuda=None)
参数介绍:
activities: torch.profiler.ProfilerActivity.CPU,torch.profiler.ProfilerActivity.CUDA
schedule:收集每一个step的信息
on_trace_ready:与schedule配合使用
record_shapes:收集形状信息
profile_memory:追踪内存使用情况
with_stack:收集其他信息,如文件与行数
with_flops:是否统计flops
with_modules:分层统计模块信息,细化到函数调用
use_cuda:是否使用GPU
- 使用方法
import os
import sys
from PIL import Image
import torch
from torchvision import transforms
from net import simpleconv3 #导入网络模型,该模型与章节5.2中相同
# 设置数据增强
data_transforms = transforms.Compose([
transforms.RandomResizedCrop(48),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.5,0.5,0.5],[0.5,0.5,0.5])
])
# 定义模型
model = simpleconv3(4)
# 对每张图像进行预测并收集性能数据
with torch.profiler.profile(
activities=[torch.profiler.ProfilerActivity.CPU],
record_shapes=True,
with_stack=True,
profile_memory=True,
with_flops=True
) as prof:
for imagepath in imagepaths: # imagepaths为图片数据的路径列表(请自行定义)
image = Image.open(imagepath)
imageblob = data_transforms(image).unsqueeze(0)
predict = model(imageblob)
print(prof.key_averages().table(sort_by="cpu_time_total", row_limit=10))
"""
key_averages() 方法会返回一个 torch.autograd.profiler.function_average 类的实例,它保存了各个操作的平均统计信息,包括操作名称、自身 CPU 时间开销占比、自身 CPU 时间开销、总 CPU 时间开销占比、总 CPU 时间开销、平均 CPU 时间、自身 CPU 内存开销、总计调用次数和总的浮点运算量等。table()用来生成一张表格,并且按照总 CPU 时间开销来排序,row_limit指定最多输出前10行。
"""
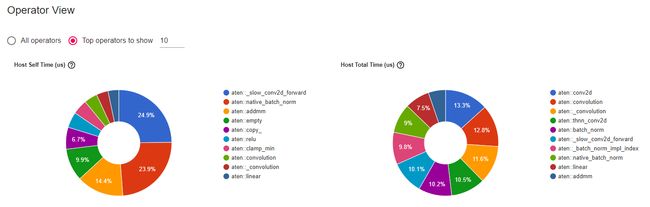
- 结果展示:
该结果包含了每个函数的自身CPU占用百分比、自身CPU时间、总CPU占用百分比、总CPU时间、CPU时间平均值、自身CPU内存占用、总CPU内存占用、调用次数和总MFLOPs。
其中,最耗费CPU时间的函数是 aten::_slow_conv2d_forward,它占用了模型总CPU时间的23.42%。第二、三、四个耗时的函数分别是aten::conv2d、aten::convolution和aten::_convolution,它们都是卷积函数。这意味着模型中的卷积操作是CPU时间最耗费的部分。
另外,aten::addmm也占用了相当多的CPU时间,它是矩阵相乘和矩阵相加的组合操作,占用了总CPU时间的11.99%。这些信息可以帮助开发者找到模型中哪些操作需要进行优化,提高模型的性能。
2. Profiler TensorBoard插件
-
安装:
pip install torch_tb_profiler -
使用:在原来的
torch.profiler.profile上添加on_trace_ready参数,用于记录
with torch.profiler.profile(
activities=[torch.profiler.ProfilerActivity.CPU],
record_shapes=True,
with_stack=True,
profile_memory=True,
with_flops=True,
on_trace_ready=torch.profiler.tensorboard_trace_handler('./log') # 添加tensorboard日志,输入日志路径
) as prof:
for imagepath in img:
image = Image.open(imagepath)
imageblob = data_transforms(image).unsqueeze(0)
predict = model(imageblob)
-
查看 tensorboard 日志:
tensorboard --logdir=./log(日志目录路径请自行修改) -
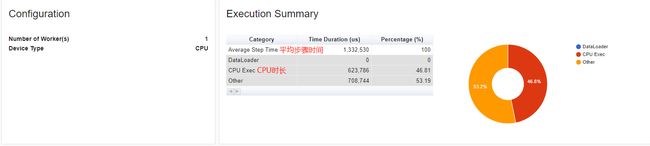
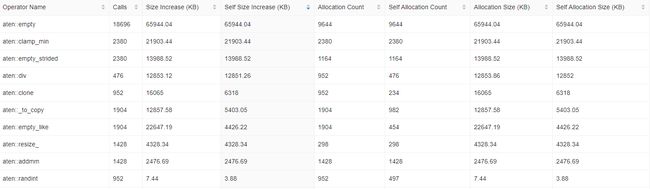
结果展示:
时间分析:
内存分析: