动手学深度学习——多层感知机

1.多层感知机

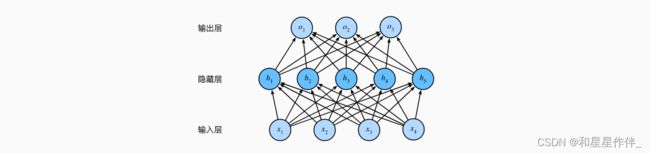
多层感知机在输出层和输入层之间增加一个或多个全连接隐藏层，并通过激活函数转换隐藏层的输出。

1.1.隐藏层

在网络中加入一个或多个隐藏层来克服线性模型的限制， 使其能处理更普遍的函数关系类型。
最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到上面的层，直到生成最后的输出——多层感知机（multilayer perceptron，MLP）:

输入：X ∈  ，表示n个样本的小批量，每个样本具有d个输入(特征)。

中间层：H ∈ ，单隐藏层，有h hh个隐藏单元，称为隐藏表示（hidden representations）。在数学或代码中，H 也被称为隐藏层变量（hidden-layer variable）或隐藏变量（hidden variable）。

因为隐藏层和输出层都是全连接的，所以我们具有隐藏层权重 和隐藏层偏置

输出层权重和输出层偏置

输出：，按如下方式计算：

为了发挥多层架构的潜力， 在仿射变换之后对每个隐藏单元应用非线性的激活函数（activation function）σ。激活函数的输出（例如，σ(⋅)）被称为活性值（activations）。 一般来说，有了激活函数，就不可能再将我们的多层感知机退化成线性模型：

虽然一个单隐层网络能学习任何函数， 但并不意味着我们应该尝试使用单隐藏层网络来解决所有问题。 事实上，通过使用更深（而不是更广）的网络，我们可以更容易地逼近许多函数。

1.2.激活函数

激活函数（activation function）通过计算加权和并加上偏置来确定神经元是否应该被激活， 它们将输入信号转换为输出的可微运算。 大多数激活函数都是非线性的。

1.2.1.ReLU函数

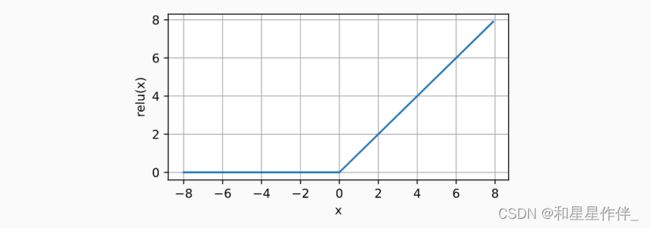
ReLU提供了一种非常简单的非线性变换。 给定元素x，ReLU函数被定义为该元素与0的最大值：

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))

 注意，当输入值精确等于0时，ReLU函数不可导。 在此时，我们默认使用左侧的导数.

y.backward(torch.ones_like(x), retain_graph=True)
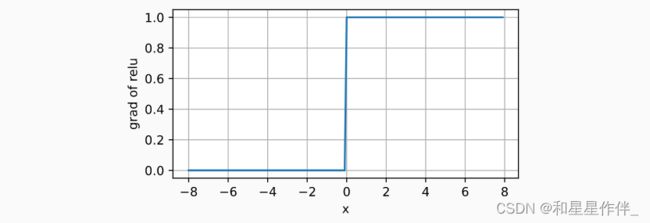
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))

retain_graph：总的来说进行一次backward之后，各个节点的值会清除，这样进行第二次backward会报错，如果加上retain_graph==True后,可以再来一次backward。如果设置为False，计算图中的中间变量在计算完后就会被释放。

使用ReLU的原因是，它求导表现得特别好：要么让参数消失，要么让参数通过。 这使得优化表现得更好，并且ReLU减轻了困扰以往神经网络的梯度消失问题

1.2.2.sigmoid函数

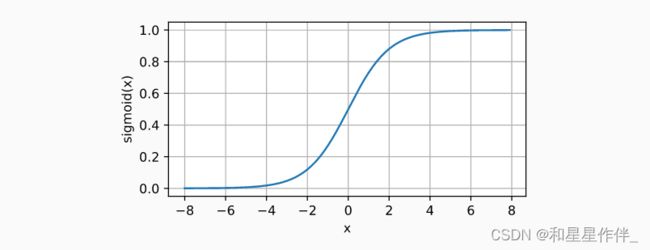
将范围(-inf, inf)中的任意输入压缩到区间(0, 1)中的某个值：

sigmoid函数是一个自然的选择，因为它是一个平滑的、可微的阈值单元近似。 当我们想要将输出视作二元分类问题的概率时， sigmoid仍然被广泛用作输出单元上的激活函数 （sigmoid可以视为softmax的特例）。

然而，sigmoid在隐藏层中已经较少使用， 它在大部分时候被更简单、更容易训练的ReLU所取代。 

y = torch.sigmoid(x)
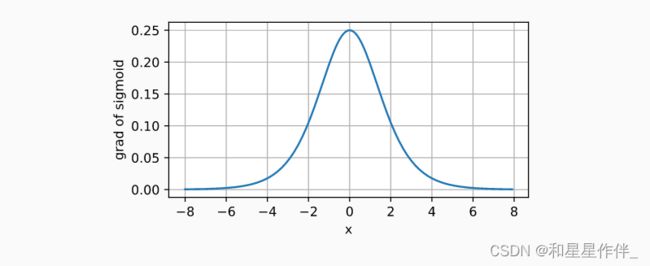
d2l.plot(x.detach(), y.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))

sigmoid函数的导数为下面的公式：

# 清除以前的梯度
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of sigmoid', figsize=(5, 2.5))

1.2.3.tanh函数

与sigmoid函数类似， tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上。 tanh函数的公式如下：

注意，当输入在0附近时，tanh函数接近线性变换。 

y = torch.tanh(x)
d2l.plot(x.detach(), y.detach(), 'x', 'tanh(x)', figsize=(5, 2.5))

tanh函数的导数是：

# 清除以前的梯度
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of tanh', figsize=(5, 2.5))

2.多层感知机的简洁实现

2.1.模型

与softmax回归的简洁实现相比， 唯一的区别是我们添加了2个全连接层（之前我们只添加了1个全连接层）。 第一层是隐藏层，它包含256个隐藏单元，并使用了ReLU激活函数。 第二层是输出层。

net = nn.Sequential(nn.Flatten(),
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

训练过程的实现与我们实现softmax回归时完全相同，此处就不附代码了

2.2.小结

对于相同的分类问题，多层感知机与softmax回归实现相同，只是增加了带有激活函数的隐藏层。

3.权重衰减

在训练参数化机器学习模型时， 权重衰减（weight decay）是最广泛使用的正则化的技术之一， 它通常也被称为L2正则化（通过函数与零的距离来衡量函数的复杂度）。

更多用于想要快速收敛的时候

3.1.简洁实现

def train_concise(wd):
    net = nn.Sequential(nn.Linear(num_inputs, 1))
    for param in net.parameters():
        param.data.normal_()
    loss = nn.MSELoss(reduction='none')
    num_epochs, lr = 100, 0.003
    # 偏置参数没有衰减
    trainer = torch.optim.SGD([
        {"params":net[0].weight,'weight_decay': wd},
        {"params":net[0].bias}], lr=lr)
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    for epoch in range(num_epochs):
        for X, y in train_iter:
            trainer.zero_grad()
            l = loss(net(X), y)
            l.mean().backward()
            trainer.step()
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1,
                         (d2l.evaluate_loss(net, train_iter, loss),
                          d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数：', net[0].weight.norm().item())

在上面的代码中，我们在实例化优化器时直接通过weight_decay指定weight decay超参数。 默认情况下，PyTorch同时衰减权重和偏移。 这里我们只为权重设置了weight_decay，所以偏置参数b不会衰减。

不使用权重衰减，这里训练误差有了减少，但测试误差没有减少， 这意味着出现了严重的过拟合。

train_concise(0)

使用权重衰减来运行代码。 注意，在这里训练误差增大，但测试误差减小。 这正是我们期望从正则化中得到的效果。

train_concise(3)

4.暂退法（Dropout）

也叫随机丢弃。

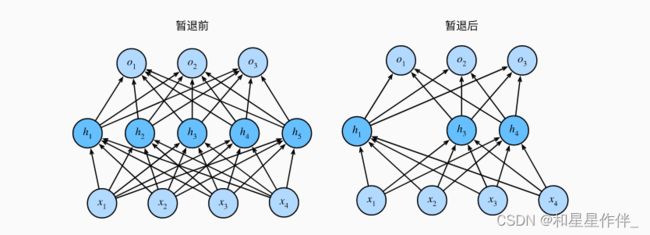
暂退法在前向传播过程中，计算每一内部层的同时注入噪声。这种方法之所以被称为暂退法，因为我们从表面上看是在训练过程中丢弃（drop out）一些神经元。 在整个训练过程的每一次迭代中，标准暂退法包括在计算下一层之前将当前层中的一些节点置零。

暂退法可以避免过拟合

4.1.简洁实现

我们只需在每个全连接层之后添加一个Dropout层， 将暂退概率作为唯一的参数传递给它的构造函数。

在训练时，Dropout层将根据指定的暂退概率随机丢弃上一层的输出（相当于下一层的输入）。

在测试时，Dropout层仅传递数据。

net = nn.Sequential(nn.Flatten(),
        nn.Linear(784, 256),
        nn.ReLU(),
        # 在第一个全连接层之后添加一个dropout层
        nn.Dropout(dropout1),
        nn.Linear(256, 256),
        nn.ReLU(),
        # 在第二个全连接层之后添加一个dropout层
        nn.Dropout(dropout2),
        nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

对模型进行训练和测试。

trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

4.2.小结

• 权重衰减和过拟合都可以用来防止过拟合。
• 暂退法在前向传播过程中，计算每一内部层的同时丢弃一些神经元。
• 暂退法将活性值h替换为具有期望值h的随机变量。