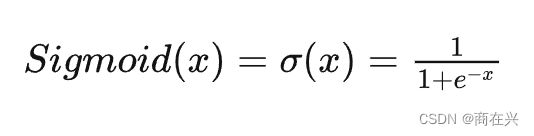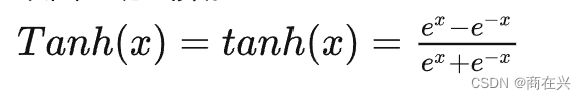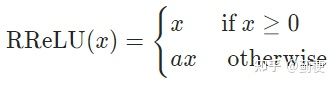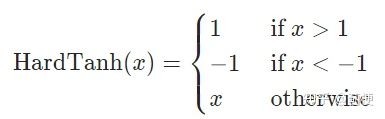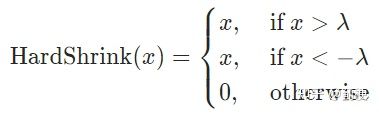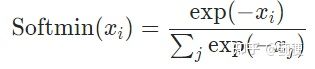【神经网络深度学习】 --激活函数
激活函数(activation function)又称非线性映射函数或是隐藏单元,是神经网络中中最主要的组成部分之一。
数据的分布绝大多数是非线性的,而一般神经网络的计算是线性的,引入激活函数,是在神经网络中引入非线性,强化网络的学习能力。所以激活函数的最大特点就是非线性。
现阶段的激活函数多种多样,对应着不同的特性。实际建模过程中,当我们需要实现不同功能时,所需要的激活函数往往也不尽相同。所以掌握各种激活函数的特性,才能在工作中按需选择、信手拈来。
1. Sigmoid
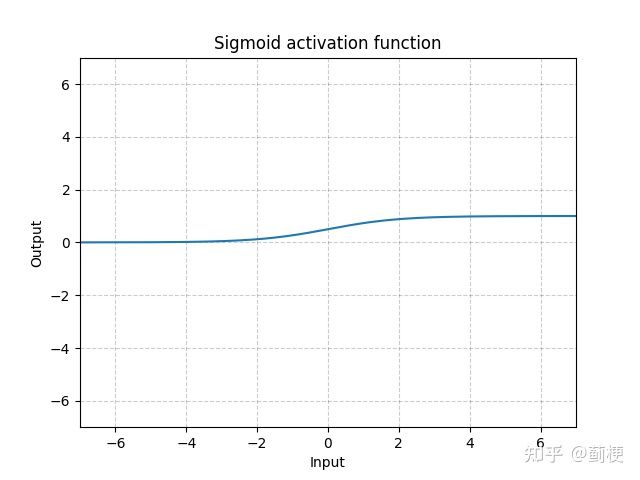
sigmoid 激活函数是深度学习中最早使用也是最常见的激活函数。多用来作为二分类的分类头。
(图片来自pytorch官方文档)
优势:
- 可导;
- 预测结果明确:距离0或1很近;
缺点:
- 容易梯度消失:多层叠加后,梯度值会非常非常小,导致收敛速度很慢,无法进行深层训练;
- 属于幂运算,计算成本很高;
- 不以0为中心,使得收敛速度变慢:考虑到sigmoid的output全大于0,当output作为下一层的输入时,wi*output=y,然后进行反向求导,此时所有的w(细节可以看这个);
(实际上,不以0为中心的问题,只要用上norm层,就可以解决了。)
2. Tanh
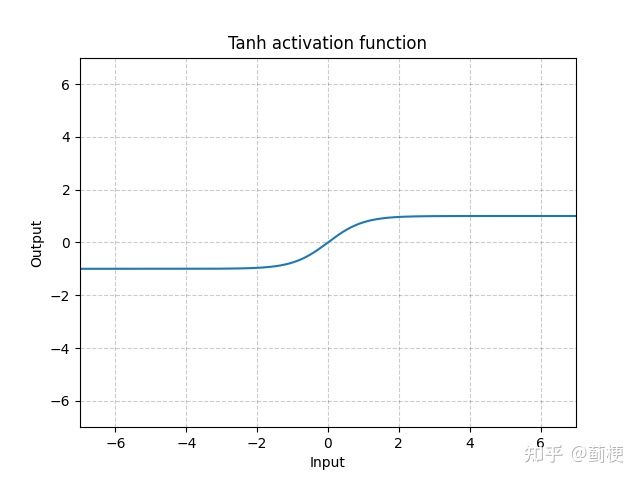
tanh的图像曲线和sigmoid类似,但它的值域是(-1, 1)。它的优势是:
- 可导;
- 以0为中心:这一点比sigmoid有优势;
但它依然存在缺陷:
- 存在幂运算:不论是正向计算还是反向传播,计算量都比较大;
- 容易梯度消失:虽然它的导数的值域是(0, 1],比sigmoid的(0, 0.25]稍有缓解,但从图上很容易看得出来,当输入值x的绝对值较大时(距离0较远时),其导数依旧会趋近于0。
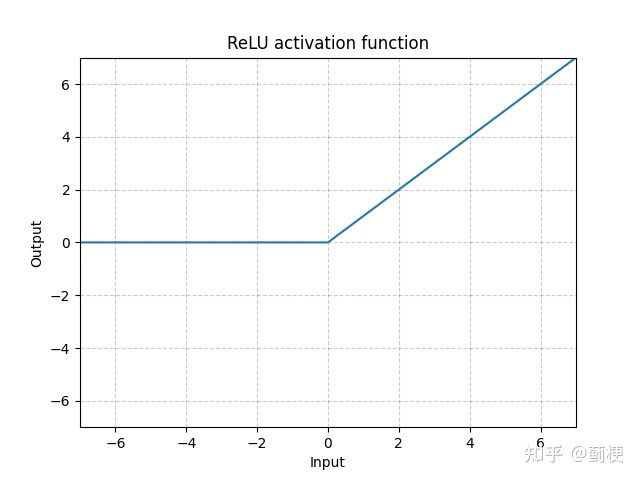
3. ReLU
rectified linear unit(整流线性单位函数),目前深度学习非常常用的激活函数,可以进行深层训练。
ReLU(x)=max(0,x)
优势:
- 没有梯度消失问题,收敛速度快:当输入input>0时,梯度会完完整整的传递给下一层,使得收敛速度远大于sigmoid和tanh;
- 计算速度快;
缺点:
- 不以0为中心(+bn层可以解决);
- 容易dying:当input大多为负值时,经过relu会变成大多为0,只剩小部分数据有能力提供梯度,导致反向传播基本不能更新参数,就会变成“dying relu(垂死的relu)”。dying relu一般由两种情况造成:1)少有的参数初始化;2)学习率太大,直接走到了大部分为负的情况。(同样,这个缺陷也可以有bn层解决,数据经过bn层后就会以0为中心,变成一半正一半负。)
通常来说relu的通用性比较好,训模型闭眼relu先。
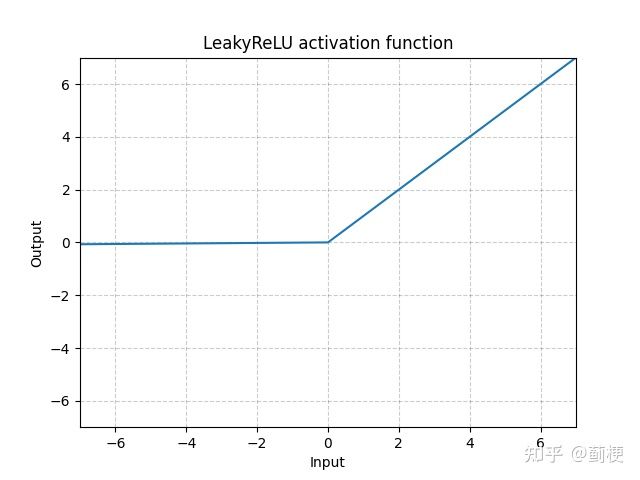
4. LeakyReLU
LeakyReLU(x)=max(0,x)+negative_slope∗min(0,x)
negative_slope 可自行设置,默认是0.01.
优势:
- 梯度不会消失;
- 计算快;
- 收敛快;
- 不会“dying”;
缺陷(理论上比relu好,实际上不一定):
- 跟relu相比,leakyrelu的优势在于不会“dying”,但这个问题已经被bn解决了,所以这方面优势不明显;
- 放弃了relu提供的特征选择的稀疏性;
用leakyrelu的模型比如Yolo系列v1~v3,都用leakyrelu作为激活层。
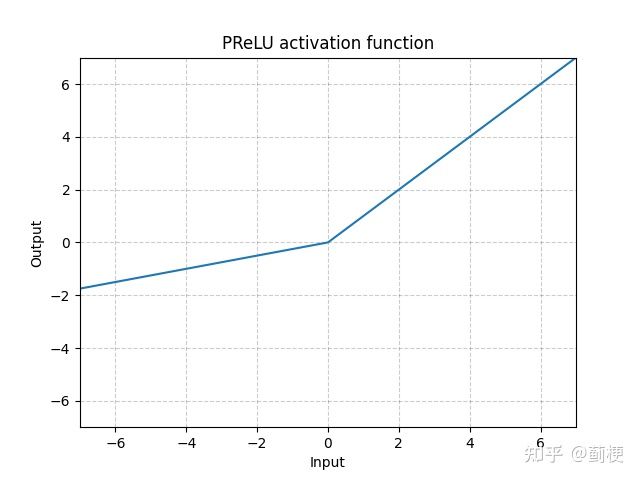
5. PReLU
就是把LeakyReLU的负斜率值negative_slope改为了可训练的参数。
拥有LeakyReLU的所有优势和缺陷。
以及:通常来说,leakyrelu比relu多一个参数,所以模型拟合能力不够时,可以用PReLU。
PReLU(x)=max(0,x)+a∗min(0,x)
在pytorch中调用nn.PReLU(num_parameters,init):
- 如果不传参,会训练一个参数a应用于所有的层;
- 如果传参(nn.PReLU(nChannels)),则会为每个通道都学到一个a。
- init可以设置初始的a,默认为0.25;
注意:当a学得性能很好时,不应使用权重衰减;
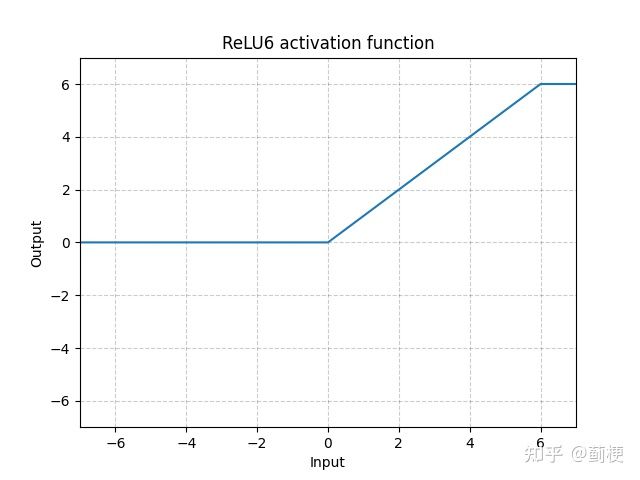
6. RELU6
ReLU6(x)=min(max(0,x),6)
优势:
- 在模型量化时有助于保持精度:在移动端(float16/int8)这种低精度机器上部署时,如果ReLU,过大的导致处理精度不够,产生较大的误差,降低模型准确率(具体细节可以看这里)。
- 防止数值爆炸;
- 增强浮点数的小数位表达能力:整数位最大是6,只占3bit,其余bit全部用来表示小数位。
使用模型:Mobilev1。
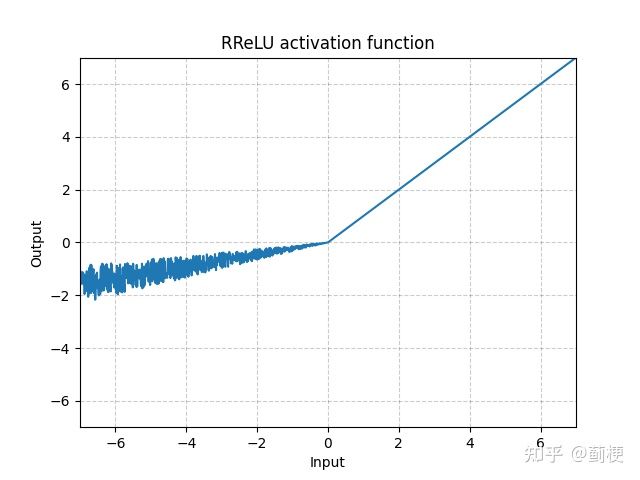
7. RRELU
其中a是一个随机数,服从均匀分布U(lower,upper)(具体细节可看https://arxiv.org/pdf/1505.00853.pdf,这篇论文对比了ReLU、LeakyReLU、PReLU和RReLU,发现RReLU在训练集上错误率最大,但在测试集上错误率最小。).
在pytorch中,nn.RReLU默认参数是(lower=1/8, upper=1/3)。
a在训练时随机,测试时固定((lower + upper) / 2)。
目前没听说哪个模型用的RReLU。
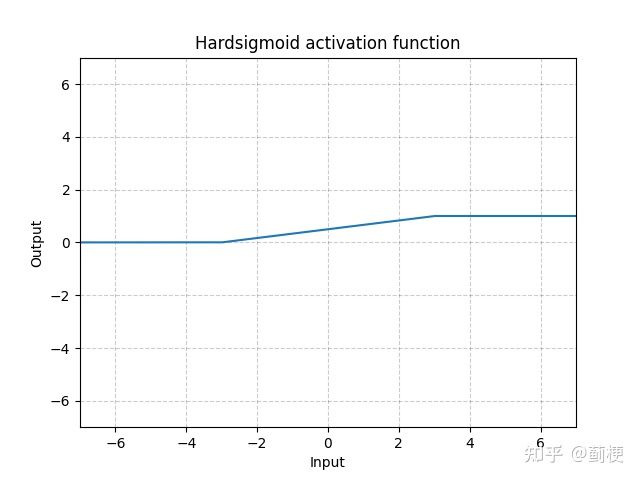
8. Hardsigmoid(硬sigmoid)
用分段函数近似sigmoid,优点是计算速度快,因为没有指数计算。
9. Hardtanh(硬tanh)
用分段函数近似tanh。
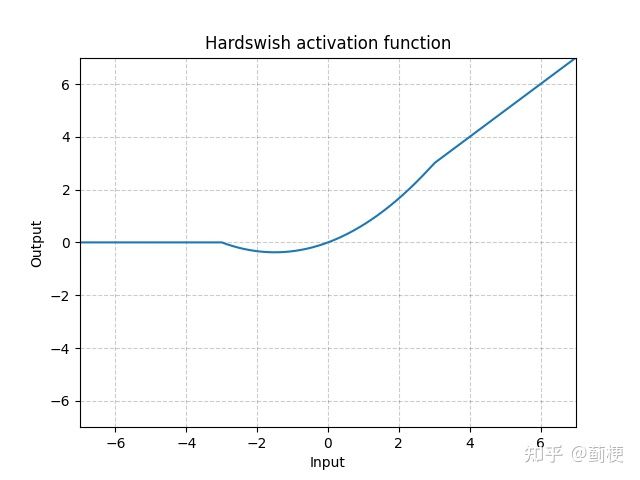
10. Hardswish
两端用线性函数近似。
使用场景:MobileNetv3.
11. Hardshrink
在pytorch中,nn.Hardshrink(lambd=0.5)。
12. ELU
很明显,优势:
- 不会梯度消失;
- 不会dying;
- 连续可导
- 收敛快;
缺点:
- 有幂计算,慢;
pytorch中nn.ELU(alpha=1.0,inplace=False)
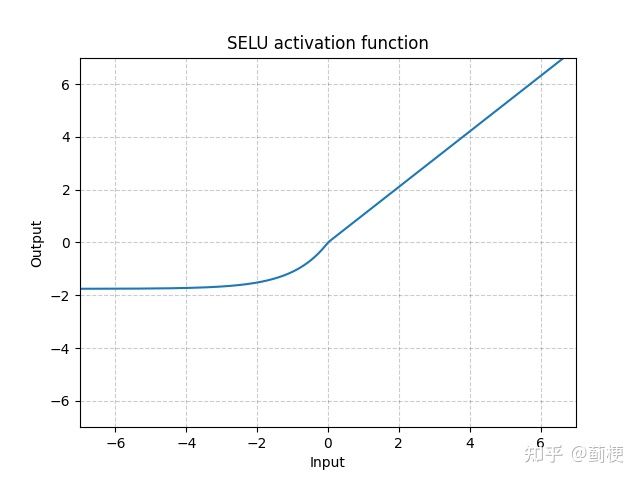
13. SELU
SELU(x)=λ∗(max(0,x)+min(0,α∗(exp(x)−1)))
其中,α=1.6732632423543772848170429916717
λ = 1.0507009873554804934193349852946
α 和 λ 的值是证明得到的,不是训出来的(详见Self-Normalizing Neural Networks,目的就是希望输入值的均值和方差分别为0和1,输出值的均值和方差也分别为0和1)。
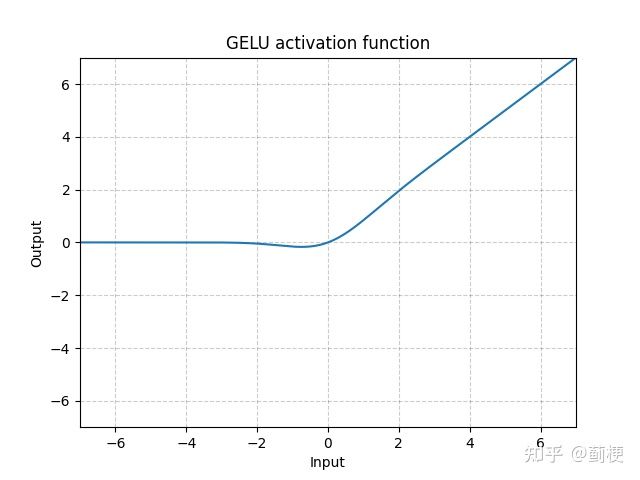
14. GELU
Gaussian Error Linear Units,高斯误差线性单元。
GELU(x)=x∗Φ(x)
其中 Φ(x) 是高斯分布的累计分布函数。
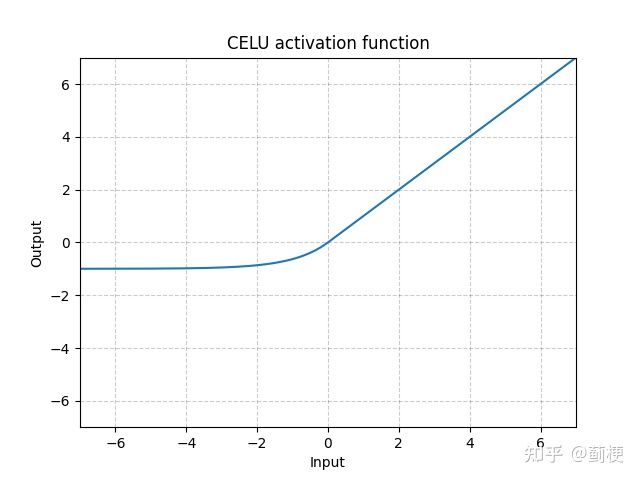
15. CELU
CELU(x)=max(0,x)+min(0,α∗(ex/α−1))
就是把ELU中的 ex 变为 ex/α 。好处是可以调整左半边的斜率了(细节详见Continuously Differentiable Exponential Linear Units)。
pytorch中α 可设置,默认是1.
16. LogSigmoid
是
17. MultiheadAttention
18. SiLU
19. Mish
20. Softplus
21.softshrink
22.softsign
23. Tanhshrink
24. Threshold
25. GLU
26. Softmax
输入n维tensor,对它们进行重新缩放(rescale)使得张量的n维输出的每个元素都在[0, 1]区间内,且和为1。此过程会保持数值原本的大小顺序,即最大值经过激活函数后依旧最大。
27. Softmin
跟softmax类似,输入n维tensor,对它们进行重新缩放(rescale)使得张量的n维输出的每个元素都在[0, 1]区间内,且和为1。不同的是,softmax是单调递增而softmin是单调递减,意味着softmax操作会使得最大的值在激活操作后依然保持最大,而softmin会使得最小的数在经过了softmin后变成最大值。
28. Softmax2d
29. Logsoftmal
30. AdaptiveLogSoftmaxWithLoss
这是一种有效的softmax逼近(如Efficient softmax approximation for GPUs by Edouard Grave, Armand Joulin, Moustapha Cissé, David Grangier, and Hervé Jégou所述)。
adaptive softmax 是一种用于训练具有大输出空间的模型的近似策略。当标签分布高度不平衡时它最有效,例如在自然语言模型中,当词频分布近似于齐夫定律(zipf's law)时。
adaptive softmax 根据标签频率把它们分成几个族群,每个族群可能包含的目标数量不同。此外,包含较少标签的族群会为这些标签分配较低维的嵌入,从而加快计算速度。对于每个minibatch,仅评估至少存在一个目标的族群。
这个想法是频繁访问的集群(如第一个,包含最频繁的标签)也应该计算成本低——即包含少量分配的标签。
如果想要了解更多,强烈建议阅读原始论文。
31. Swish
:y = x * sigmoid (x)