论文阅读笔记：Cold Filter A Meta-Framework for Faster and More Accurate Stream Processing

论文阅读笔记：Cold Filter: A Meta-Framework for Faster and More Accurate Stream Processing

​ 这篇文章是北大杨仝老师课题组发表在SIGMOD2018上面一篇文章，提出了一种两层过滤的方式，将cold items记录在第一层，hot items记录在第二层，实现过滤出hot items作用，并与常用sketch结合进行估计：CM，CM-CU，Space-Saving，FlowRadar，ASketch。github代码地址：https://github.com/zhouyangpkuer/ColdFilter

Abstract

​ 近似流处理算法(Approximate stream processing algorithm)，例如：Count-min sketch、Space-Saving 在数据库、存储系统、网络中又很多应用。存在问题：真实数据流的不均衡分布(unbalanced distribution)对现存算法提出很大挑战。目的：为了增强这些算法，提出了一个元框架(meta-framework)，叫做Cold Filter(CF)，可以实现更快、更准确的流处理。

​ 核心思想：不同于现存过滤器仅聚焦于hot items，我们的过滤器在第一层捕捉cold items，在第二层捕捉hot items。区别：现存过滤器需要双向通信(two-direction communication)，在两个层次间频繁交换。我们的过滤器是单向的(one-direction)，每个项目最多进入一个层次一次。Cold Filter可以准确地估计冷项目和热项目，使其具有通用性，使其适用于许多流处理任务。效果：将其部署在3个经典的流处理任务上(typical stream processing tasks)，速度和准确性大幅提升。

1. 背景

​ 大数据场景下，数据以高速流(hith-speed stream)的形式到达，这样的数据流通常是单次处理。在许多应用中，需要在数据流的每个时间窗口中提供一些统计信息，例如item frequency, top-k hot items, heavy changes, and quantiles(分位数)。存在问题：然而，计算精确的统计数据(例如，使用哈希表)通常是不切实际的，因为存储整个数据流的空间和时间成本太高。因此，概率数据结构(probabilistic data structures)在近似处理中(approximate processing)变得更加流行。

​ 挑战：数据流到达的速度和它们的大小(size) 一起使得近似流处理(approximate stream processing)具有挑战性。1) 处理的内存使用应该足够小，以适应有限大小和昂贵的SRAM(静态RAM，如CPU缓存)，从而实现高处理速度。2) 必须一次处理数据(in a single pass)，这极大地限制了必须进行处理的速度。3) 为了保证应用的性能，精度要尽可能的高。

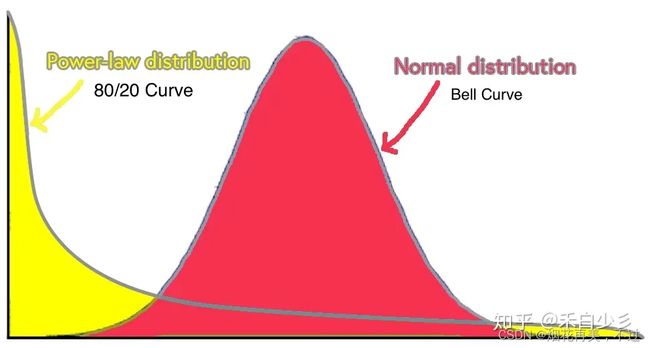
​ 真实数据流特征：实际数据流中的项目往往服从不平衡分布(unbalanced distribution)，如Zipf(齐夫分布)或Power-law(幂律分布) 。这意味着大多数项目是不流行的(称为cold items)，而少数项目非常流行(称为hot items)。我们把这样的数据流称为倾斜数据流(skewed data streams) 。这样的特征对流处理任务产生极大挑战。流处理任务划分为两类：1) 需要准确记录hot and cold items，如估算项目频率(estimating item frequencies)，以及项目频率分布(item frequency distribution)。2) 只需要准确地记录hot items，例如top-k和 heavy changes。

齐夫分布(Zipf distribution) 是一种典型的幂律分布，从语言中词汇的出现频率，到国家人口在不同规模城市间的分布，再到网页访问频率、收入的排序，都遵循齐夫定律。齐夫定律是哈佛大学语言学家乔治·齐夫（George Zipf）1949年发现的一个实验定律，即在自然语言里，一个单词出现的频率与它在频率表里的排序成反比。 例如，在英语的 Brown 语料库中，「the」、「of」、「and」是出现频率最高，排序 1、2、3 的单词，分别占整个语料库100万个单词数的 7%、3.6%、2.9%[1]。可见排序第2位「of」的频率大约是第1「the」的1/2，第3的「and」是其 1/3。以此类推，排序第n单词的频率是最常见频率的1/n。最简单的齐夫定律排序遵从一次反比即 1/f 关系。由此可以得到它的等价描述：

在给定语料中，对于任意一个单词，其频率（Frequency）与频率排序（Rank）乘积大致是一个常数，即：Rank * Frequency ≈ Constant。齐夫定律是一种典型的幂律分布，更确切说是另一种统计分布帕累托分布（Pareto distribution）的特例。后者亦称帕累托定律，最形象的描述为「二八定律」：任何国家的20％的人口拥有80％的国民财富，完成80％的工作需要20％的工作量等。这些分布都反映了一种普遍的「穷者愈穷，富者愈富」的幂律现象。在齐夫定律中，则是第1富有的是第n富有的n倍。

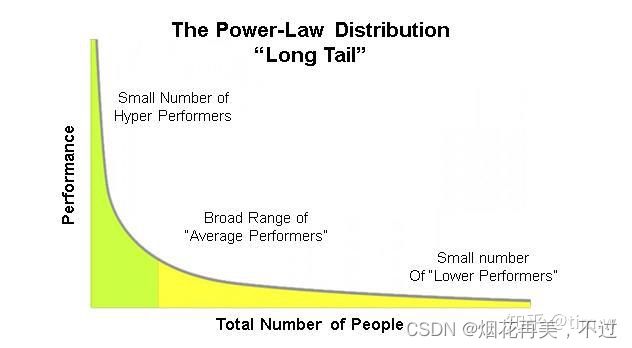
幂律分布(power-law) ：幂律法则指在任何一件事物中，极少数的关键事物带来绝大多数的收益，其他大多数普通事物只获得少量收益。平时经常能见到的马太效应，长尾理论，帕累托法则（上面所说的二八法则）其实就是和幂次法则的意思差不多。通过幂律分布图表的形态我们能够的看出，对一件事情起决定作用的，往往是少数几个因素，而其它大部分的因素都无关紧要。除了财富，与人类社会相关的分布大多都是符合幂律分布的。
例如，某书店如果按销量排列，就能发现主要销量都集中在少量热门书籍上，而其余大部分书籍的销量只占总销量剩下的其他部分；又比如，英文的学习中，只有20%的词汇会经常用到，而剩下80%的词汇可能用得比较少，学习的时候可以优先把常用词汇先搞定，其它词汇用日常的时间来不断消化。看到这里相比大家会问，这不就是二八法则么？是的，我们常能听到的二八法则其实就是幂律分布思维模型使用方式的一种。

​ 3类关键的流处理任务：

​ Estimating Item Frequency: 两个经典的解决方案：Count-Min sketch和CM-CU sketch。存在缺陷：它们都使用一些固定大小的计数器来存储项目的频率。如果每个计数器都很小，则无法记录超出计数器最大值的热点项目频率。这是很难接受的，因为热门项目在实践中往往被认为更重要。如果每个计数器足够大以容纳最大频率，那么大多数计数器的高比特位将被浪费，因为在实际数据流中，热项(hot items)比冷项(cold items)少得多。

​ Finding Top-k Hot Items: 由于我们不能存储所有传入的项目，并且只能处理每个项目一次，最先进的解决方案Space-Saving，近似将top-k项保存在一个称为Stream-Summary的数据结构中。给定一个即将到来的不在Stream-Summary中的项目，Space-Saving假设它比Stream-Summary中的最小值稍大一点，并交换它们，以实现快速的处理速度。缺陷：大部分项目都是冷的(cold items)，每一个冷的项目(cold items)都会进入Stream-Summary，可能保留也可能驱逐。频繁的交换会降低top-k结果的准确性，这是由冷项目引起的，应该避免。

​ Detecting Heavy Changes：一些项目的频率可能会在短时间内发生显著变化。检测这些项目对于搜索引擎和安全都很重要。先进的方案是FlowRadar，依赖于Invertible Bloom Lookup Table(IBLT)。它使用IBLT在两个相邻的时间窗口内大致监测所有传入项目及其频率，然后比较它们的频率并得出结论。缺陷：如果有足够的内存来记录每个项目，FlowRadar可以实现高精度，这在许多情况下可能是不切实际的。实际上，在每个时间窗口中，都有大量的冷项，这些冷项没有必要记录，并且比热项占用更多的内存。

​ 总结：倾斜数据流(skewed data streams)的特点使得最先进的算法很难很好地工作或需要大量的资源。为了应对这一挑战，有几种算法可以对数据流进行过滤，如Augmented sketch、skimmed-sketch。原理：它们使用类似CPU cache的机制:在第一层首先处理所有项目，然后将cold items交换到第二层。优势：可以有更少的内存访问。缺陷：很难准确捕获hot items，因为所有hot items最初都是冷的，并存储在第二层，然后变热。现有的算法需要采用双向通信的方式来实现，两个层次之间的交换和通信频繁。1) 它们在第一层使用堆或表，因此通常需要多次内存访问来处理每个项目; 2) 第一层只能捕获少量热点项目(例如ASketch中的32个热点项目)，因为更多的热点项目需要更多的内存访问; 3) 它们使执行管道并行变得困难。

​ 设计目标：设计一种依赖单向通信的过滤器，以准确估计热项和冷项为目标，处理速度更快。

​ 数据结构：Cold Filter(CF)使用带有小计数器的两层sketch来准确记录cold items的频率，如果所有哈希到的计数器溢出了，CF将会报告传入的项目作为hot item(单向通信one-direction communication)，然后把它发送到现存的流处理算法中(the CM-CU sketch、Space-Saving、FlowRadar)。元框架(meta-framework) ：因为我们可以以不同的方式将CF与现有的不同算法结合起来，并获得很大的好处。第一层只使用小计数器来存储冷项目的频率，因此内存效率很高。通过过滤掉大量的冷项，第二层集中在热项上，因此可以达到很高的精度。为增强处理速度，提出的技术：1）aggregate-and-report(including SIMD parallelism)、2）one-memory-access、3）multi-core parallelism。由于我们的Cold Filter可以准确记录both cold item and hot item的信息，因此适用于大多数流处理任务。

2. 相关工作

​ sketch被广泛应用于估计数据流的项目频率。Count-Min sketch应用最广，它依赖于$d$个数组$A_1\dots A_d$，每个数组包含$w$个计数器。这里有$d$个哈希函数，$h_1\dots h_d$在Count-Min sketch中。当插入一个频率为$f$的项目$e$，Count-Min sketch会增加所有$d$个映射的计数器$A_1[h_1(e)]\dots A_d[h_d(e)]$增加$f$。当查询一个项目$e^{\prime }$时，它将$d$个哈希映射到的计数器的最小值报告为该项目的估计频率，即$mi{n}_{1\le i\le d}\{A_i[h_i(e^{\prime })]\}$。CM-CU sketch实现了更高准确性，唯一区别在于CM-CU仅增加d个映射到的计数器的最小值。CM和CM-CU均没有低估误差。

​ 问题：那这里的CM-CU sketch是不是和CU sketch极其相似了，但我看参考文献不是一篇论文。

​ 与cold filter最相关的工作是Augmented sketch。它添加了一个额外的过滤器(一个有k个项目和计数器的队列)到现存的sketch $\varphi$，去保持最频繁的项目在这个计数器中。当插入项e时，它逐个扫描存储在过滤器中的项。如果e已经在过滤器中，它只增加相应的计数器。否则，如果过滤器中有可用空间，它将以初始计数1存储e。如果没有可用空间，即过滤器已满，则将此项插入到sketch $\varphi$ 中。在插入期间，如果 $\varphi$ 报告的该项的频率大于过滤器中的最小值(与项$e^{\prime }$相关联)，则Augmented sketch需要将项$e^{\prime }$排除 $\varphi$，并将e插入过滤器。

3. Cold Filter 元框架

​ Problem statement：给定一个数据流$S=(e_1,e_2,\dots ,e_E)$和一个现在的时间点$t$，当前子流是$S_t=(e_1,e_2,\dots ,e_t)$。对于当前项目$e_t$，如何准确和快速的估计是否它的当前频率$f_{e_t}[t]$超过了给定的阈值 $\tau$ ？

3.1 A Naive Solution

​ 一个简单的解决方案是使用sketch $\varphi$ (例如，Count-Min sketch，CM-CU sketch等)作为CF。具体来说，我们使用 $\varphi$ 记录从时间点1开始的每个项目的频率。对于每个传入项目，我们首先查询$\varphi$，并获得其估计频率。然后我们检查这个估计的频率是否超过阈值 $\tau$。然而，这种解决方案在实际数据流中存在内存效率低下的缺点。假设 $\tau$ = 1000。对于 $\varphi$，我们将其计数器大小设置为16，它可以计数频率高达65535。但是在真实的数据流中，大多数项目的频率都很低，不能“填满”它们被散列到的计数器。因此，$\varphi$ 的大多数计数器中的许多高阶位都被浪费了，这意味着内存效率低下和过滤性能次优。

​ 如果我们可以为cold item自动分配小计数器，为hot item自动分配大计数器，那么分配的内存就可以得到充分利用。这就是我们提出的解决方案所实现的。

3.2 提出的解决方案

3.2.1 两层Cold Filter的数据结构

​ Cold Filter(CF)由两层组成：一个低层$L_1$(low layer)，一个高层$L_2$(high layer)。这两层分别由$w_1$和$w_2$个计数器组成，分别联系$d_1$和$d_2$个哈希函数$(h(.)$和$ g(.))$。第一层 $L_1$ 和第二层$L_2$每个计数器的大小分别是 ${\delta }_1$ 和${\delta }_2$。我们将阈值$\tau$分为两部分：$\tau ={\tau }_1+{\tau }_2(1\le {\tau }_1\le 2^{{\delta }_1}-1,1\le {\tau }_2\le 2^{{\delta }_2}-1)$。

3.2.2 Cold Filter更新过程

​ $V_1$表示在低层$L_1$映射的$d_1$个计数器中的最小值，$V_2$表示在高层$L_2$映射的$d_2$个计数器中的最小值。如果$V_1<{\tau }_1$，Cold filter增加低层$L_1$中映射的最小计数器加1。注意如果这里有多个计数器有相同的最小值，它们所有都应该被增加。在更新过程中，$d_1$个哈希计数器的值可能是不同的，然而只增加最小计数器的操作总是缩小$d_1$个散列计数器值的差异。如果当这些$d_1$个散列计数器中的一个或多个值达到${\tau }_1$时，则所有后续增量将添加到其他计数器中。因此，最终状态是所有$d_1$个散列计数器将同时地到达${\tau }_1$。我们称这种状态为并发溢出状态(the concurrent overflow state)。当达到这个状态时(即$V_1={\tau }_1$)，CF通过高层(high layer)记录该项目信息。

​ 对于低层(low layer)处于并发溢出状态的$d_1$个哈希计数器，我们提出了一种新的策略:保持它们不变(keep them unchanged)。这种策略使得不需要使用额外的标志来指示并发溢出状态，这对于CF上的后续查询操作是至关重要的。高层的更新操作与低层类似，如果$V_2<{\tau }_2$，Cold filter增加最小的哈希到的计数器增加1。

3.2.3 Cold filter报告过程

​ 如果果哈希的计数器在更新之前同时在两层(高层和低层)溢出，Cold Filter报告$f_{e_t}[t]>\tau$；否则，Cold filter报告$f_{e_t}[t]\le \tau$。注意$f_{e_t}[t]=f_{e_t}[t-1]+1$。报告过程如下：

（1）如果$V_1<{\tau }_1$，我们有$f_{e_t}[t-1]\le V_1<{\tau }_1<\tau$。因此我们报告$f_{e_t}\le \tau$。

（2）如果$V_1={\tau }_1$但是$V_2<{\tau }_2$，我们有$f_{e_t}[t-1]\le V_1+V_2<{\tau }_1+{\tau }_2=\tau$。因此我们也报告$f_{e_t}[t]\le \tau$。

（3）如果$V_1={\tau }_1$并且$V_2={\tau }_2$，存在两种情况：

​ （a）$f_{e_t}[t-1]\ge \tau$并且因此$f_{e_t}[t]$确定超过$\tau$。我们应该报告$f_{e_t}[t]\le \tau$。

​ （b）$f_{e_t}[t-1]<\tau$，但是哈希冲突导致$V_1={\tau }_1$并且$V_2={\tau }_2$。我们应该报告$f_{e_t}[t]\le \tau$。

​ 区分这两种情况并不容易。为了节省空间和时间，我们选择只报告$f_{e_t}[t]>\tau$。

3.2.4 示例

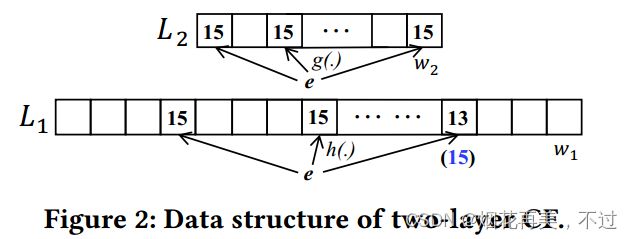
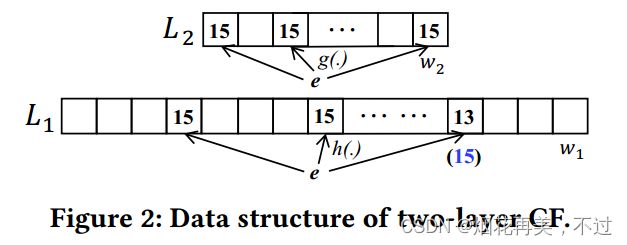
​ 我们设置第一层和第二层哈希函数数量$d_1=d_2=3$，第一层和第二层计数器位数${\delta }_1={\delta }_2=4$，第一层和第二层阈值${\tau }_1={\tau }_2=15$。对于传入的项目$e_t$：

​ （1）如果在第一层$L_1$中3个哈希的计数器是15，15，13。我们可以得到$V_1=min\{15,15,13\}=13$。然后我们增加第一层$L_1$的第三个哈希计数器加一，并且报告$f_{e_t}[t]\le \tau$。 （2）如果在第一层$L_1$的3个哈希计数器是15，15，15(在蓝颜色的)。我们可以得到$V_1=min\{15,15,15\}=15={\tau }_1$。然后我们需要访问第二层$L_2$。假设在第二层$L_2$它的3个哈希的计数器是15，15，15。我们得到$V_2=min\{15,15,15\}=15={\tau }_2$。然后我们需要报告$f_{e_t}[t]>\tau$。实现的目的：这个例子中的总阈值是$\tau ={\tau }_1+{\tau }_2=15+15=30$ ，如果一个项目频率小于30的话就保存在cold filter中，即所谓的cold items，只有当cold filter中这两层同时溢出了意味着这个项目频率大于30，我们将其保存到计数器位数更大的sketch当中，即所谓的hot items。同时也解决了这个矛盾：如果所有计数器都用固定大小，由于流的重尾分布会造成空间浪费；如果都采用位数较小的计数器，造成无法统计大流计数，不准确。

​ 这个方案不会导致假阴性(false negative)，只有小部分的假阳性(false positives)。如果$f_{e_t}[t]$的确超过了阈值$\tau$，Cold filter将会确定识别这个过量(no false negative)。对于频率$f_{e_t}[t]$不超过阈值$\tau$的一小部分项目，CF可能得出错误的结论(false positives)。

当你真的没有的时候，别人却说你有—假阳性(false positive)

当你真的有的时候，别人却说你没有—假阴性(false negative)

下面表格列出了四种情况，另外两张判断正确的情况分别是：

你真的有，别人也说你有—真阳性（true positive）

你真的没有，别人也说你没有—真阴性(true negative)

所以，我们可以看到true和false其实是：实际情况和判断的是否一致，如果一致的话，就是true；如果不一致的话，就是false；而positive和negative则是针对判断的情况：如果判断是“有”、“存在”等肯定意义的情况，则是positive；如果判断是“没有”、“不存在”等否定意义的情况，则是negative。

参考文献： 理解 假阳性（false positive）和假阴性(false negative）概念-CSDN博客

​ 假设阈值$\tau =1000$，对于以前解决方案中的sketch $\varphi$，我们设置它的计数器大小是16比特，$w$表示 $\varphi$ 中计数器的数量。对于我们提出的两层Cold filter，我们设置第一层计数器位数${\delta }_1=4$位，第二层计数器位数${\delta }_2=16$位，第一层阈值${\tau }_1=15$，第二层阈值${\tau }_2=985$，${\tau }_1+{\tau }_2=1000$。我们分配50%内存给第一层$L_1$(假设2M)，分配50%内存给第二层$L_2$(假设2M)。那对于以前解决方案技术器的数量是$4M/16bit=2^{18}$个。对于Cold filter第一层$L_1$的计数器数量是$2M/4bit=2^{19}$，因此Cold filter第一层计数器数量是以前解决方案计数器数量的两倍。因此，在$L_1$层，两层CF可以实现更低的哈希冲突，从而更少的冷项将被误报。由于一个项目访问$L_2$层的平均概率非常低(当${\delta }_1=4$时，在实际数据流中通常小于1/20)，$L_2$层仍然存在较低哈希碰撞。

3.3 优化1：聚合并且报告(Aggregate-and-report)

​ 在真实的数据流中，一些项目经常在多个连续时间点上多次出现。这被称为stream burst，提供了一个机会去加速Cold filter。Aggregate-and-report核心思想：添加另一个小过滤器，在Cold filter之前聚合突发项(aggregate the bursting items)，然后在特定条件下向Cold filter报告聚合项及其频率(通常大于1)。这个小过滤器可以通过ASketch实现：扫描整个队列并且驱逐有最小频率的项目。这种方法缺陷：如果队列比较大，这种方法的速度会比较慢。更糟糕的是，它需要双向处理-过滤器和它背后的sketch之间频繁的交换，这是昂贵的。我们的做法：我们通过使用一个改进的有损哈希表(modified lossy hash table)实现一个单向过滤器(one-direction filter):每个项目被哈希到一个桶中，每个桶由几个项目及其相应的频率组成。我们使用SIMD (Single Instruction Multiple Data)来扫描一个特定的桶。

​ 实现Aggregate-and-report的数据结构：这里有$d_b$个桶(bucket)，每个桶由$w_c$个单元格(cell)组成，每个cell存储一个键值对(key-value pair)。键的部分记录项目ID，值的部分记录了对应项驻留在该桶中的时间窗口内累积的聚合频率(aggregated frequency)。对于每个传入的项目，我们使用一个哈希函数定位一个bucket，然后进行桶扫描操作(bucket scan operation)。

​ （1）如果一个单元格的键部分与传入项目的ID匹配，则增加相应的值部分;

​ （2）否则，如果有可用的单元格，我们将频率为1的当前项插入到新的单元格中;

​ （3）否则，我们将以全局轮询方式(在$d_b$个桶之间)剔除该存储桶的一个单元格(cell):将此单元格的键(key)部分替换为传入项的ID，并将此单元格的值部分设置为1。从桶中被驱逐的带有聚合频率的项将被插入到Cold Filter中。

​ 此外，在每个时间窗口结束时，我们需要将所有桶中的所有项目冲洗到Cold filter中。设$f_{agg}$为报告的任意项目的聚合频率的值。由于$f_{agg}$通常大于1，我们需要对算法1做一些修改。

3.4 优化2：一次内存访问(One-memory-access)

​ 每个传入项目需要访问第一层$L_1$，少数项目需要访问第二层$L_2$。访问$L_1$层需要$d_1$次内存访问和哈希计算，很可能成为系统瓶颈。为了解决这个瓶颈，我们提出了仅针对$L_1$层定制的一次内存访问策略。一次内存访问策略分为两部分：（1） 我们将$d_1$个哈希计数器限制在一个$W$位的机器字内，以减少内存访问；（2） 我们只使用一个哈希函数来定位d1个哈希计数器，从而减少哈希计算。（3） 具体来说，我们将哈希函数产生的值分成多个段，每个段用于定位机器字或计数器。例如：对于第一层$L_1$,有计数器数量$w_1=2^{20}$, 每个计数器包含位数${\delta }_1=4$, 第一层哈希函数数量$d_1=3$（内存使用时1MB)。我们将32位哈希值拆分为四个段:一个16位段和三个4位段(丢弃剩余的4位)。我们使用16位值来定位$L_1$层的一个机器字，使用三个4位值来定位该机器字内的三个计数器(包含$16=2^4$个计数器)。在实践中，64位哈希值总是足够的。

4. Cold filter 部署

4.1 估计项目频率(Estimating Item Frequency)

​ 核心思想：对于频率估计，我们使用CF来记录冷项目的频率，并使用sketch $\varphi$ (例如，Count-Min Sketch，CM-CU Sketch等)来记录热项目的频率。

​ 插入：在插入项时，我们首先按照前面描述的更新CF。如果在插入之前，哈希计数器在两层同时溢出，我们使用sketch $\varphi$ 记录该项的剩余频率。

​ 查询：$V_1$和$V_2$分别表示Cold filter两层中映射计数器的最小值，$V_{\varphi }$表示sketch $\varphi$ 的查询结果。当查询一个项目时，有3种情况：1） 如果哈希的计数器在$L_1$层没有同时溢出($L_1<{\tau }_1$)，这种情况说明项目信息只记录在$L_1$ 层，所以我们报告$V_1$，当第一层映射的计数器刚好都达到溢出状态此时$V_1={\tau }_1$ 。2） 如果哈希的计数器在$L_1$层同时溢出($V_1={\tau }_1$)，但是第二层$L_2$没有同时溢出，这种情况说明项目信息同时记录在$L_1$ 层和$L_2$ 层，所以我们报告$V_1+V_2$。3） 否则，说明项目信息同时记录在$L_1$ 层、$L_2$ 层和 Sketch $\varphi$ 中，所以我们报告$V_1+V_2+V_{\varphi }$。

​ 讨论：为什么使用Cold filter的sketch可以达到比标准sketch更高的精度？原因：用于估计项目频率的常规草图不能区分冷项目和热项目。它们使用由最大频率决定的固定大小的计数器进行计数。由于实际数据流中的热项目比冷项目少得多，因此大多数计数器的高位数将被浪费(内存效率低下)。

​ 如果我们使用CF近似区分cold items和hot items，那么我们就可以利用计数器中的倾斜。对于热门项目，我们使用另一个带有大计数器的sketch来记录其频率。对于冷项目，带有小计数器的CF提供了更准确的估计，因为它利用了与CM-CU sketch相似的更新策略，同时包含了更多的计数器。采用不同大小的计数器进行计数，可以保证存储效率，从而提高精度。

4.2 寻找Top-k 热点项目(Finding Top-k Hot Items)

​ 以前方法(Prior art) :有两种找top-k热点项目的方法：基于sketch和基于计数器的。基于sketch的方法使用一个sketch(即Count-Min sketch，CM-CU sketch)去记录数据流中每个项目的频率，使用一个大小为k的最小堆(a min-heap of size k)维持一个top-k 热点项目。基于计数器的方法：包括Lossy Counting, Frequent algorithm, Space-Saving。

​ Space-Saving:维持了一个数据结构叫做Stream-Summary，由$H(H\ge k)$个项目-计数器对组成(item-counter pairs)。对于每个传入项目e，如果e已经被Stream-Summary监控，它只增加相应的计数器。否则，如果有可用空间，它会将e插入到Stream-Summary中。如果没有可用的空间，它通过从Stream-Summary中驱逐具有最小计数(Cmin)的项目来创建新的空间，并在该空间中存储计数为$C_{min}+1$的e。在查询过程中，Space-Saving根据它们记录的频率从Stream-Summary中返回top-k热点项目。

​ 核心思想：为了提高Space-Saving的性能，我们使用CF来防止大量的冷项访问Stream-Summary。

​ 插入：在插入项时，我们首先按照前面的描述更新CF。如果在插入之前，哈希计数器在两层同时溢出，我们将把该项提供给Space-Saving。

​ 报告：在处理完数据流中的所有项目后，我们从Stream-Summary中获得top-k热门项目的id和记录频率。它们的估计频率将等于相应的记录频率加上阈值 $\tau$ 。

​ 讨论：为什么使用CF的Space-Saving比标准的Space-Saving能达到更高的精度？原因：标准Space-Saving对每个项目进行相同的处理:每个传入的项目都需要送到Stream-Summary。不幸的是，大量的冷项将导致Stream-Summary中许多不必要的交换，使得记录的频率高度高估，因为每次交换都会导致与被驱逐项相关的计数器中的一次增量操作。对频率的过高估计进一步导致Stream-Summary中出现许多不正确的交换。如果我们使用CF来过滤掉大量的冷项，那么在Stream-Summary中就会出现更少的错误交换，并且可以提高记录频率的准确性。

4.3 检测重大变化(Detecting Heavy Changes)

​ 以前方法：Heavy changes指的是指在两个连续时间窗之间经历频率突变(abrupt changes)的项目。我们也称这些项目为culprit(罪犯，犯人) items。假设在第一个时间窗口数据流存在频率向量：$f_1=<f_{1e_1},f_{1e_2},\dots ,f_{1e_L}>$，$f_{1e_i}$表示项目$e_i$的频率。在第二个时间窗口我们有$f_2=<f_{2e_1},f_{2e_2},\dots ,f_{2e_L}>$。对于项目$e_i$，如果$|f_{1e_i}-f_{2e_i}|\ge \varphi \cdot D$，$\varphi$是预定义的阈值，$D={\sum }_{j=1}^L|f_{1e_j}-f_{2e_j}|$ ，这被称作一个heavy change。方法有：The key-ary sketch，The reversible sketch，FlowRadar。

​ FlowRadar: 借助一个布隆过滤器(bloom filter)在一个可扩展IBLT(Inversible Bloom Lookup Table)中快速编码每个不同的项目及其频率，并以O(n)的时间复杂度解码它们，其中n是不同项目的数量。当可扩展的IBLT中使用的哈希函数数设置为3,FlowRadar可以以非常高的概率解码所有项目。显然，FlowRadar可以通过比较两个解码的项目集来检测重大变化(heavy changes)。

​ 关键思想：为了提高FlowRadar的性能，我们使用CF来防止大量的冷项访问FlowRadar。

​ 插入：在第一个时间窗口中，当插入一个项目时，我们首先像前面描述的那样更新CF。如果在插入前这两层的散列计数器同时溢出，则需要将该项插入FlowRadar。在此时间窗口结束时，我们使用CF和FlowRadar的新实例。所述第二时间窗口内的插入过程与所述第一时间窗口内的插入过程相同。

​ 报告：在第二个时间窗口结束时，我们对FlowRadar中与每个时间窗口相关的两个IBLT进行解码。$S_1$和$f_1^I$分别表示从第一个IBLT解码出来的项目集合(item set)和频率向量(frequency vector)。对于每个项目$e\in S_1,f_{1e}^I$是在IBLT记录的频率。类似的，我们从第二个IBLT得到$S_2$和$f_2^I$。$V_1$和$V_2$分别表示CF中两层哈希到的计数器的最小值。对于任一项目$e\in S_1\cup S_2$，我们定义对于第一个CF的函数$Q_1(.)$：1）如果哈希的计数器在第一层$L_1$没有同时溢出，$Q_1(e)=V_1$；2）否则，$Q_1(e)=V_1+V_2$。类似的，我们定义$Q_2(.)$对于第二个CF。

​ 讨论：为什么使用了CF的FlowRadar需要更少的内存比标准的FlowRadar？原因：FlowRadar中IBLT的内存使用量应该与它记录的不同项目的数量成正比。因此，大量不同的冷项目将导致标准FlowRadar的大量内存消耗。如果我们使用CF过滤掉冷项，FlowRadar需要记录的不同项的数量将大大减少，并且可以节省大量内存。

5. Cold filter的正式分析

​ 标准布隆过滤器：标准的Bloom过滤器可以判断一个项目是否出现在一个集合中。它由与d个哈希函数相关联的w位数组组成。当插入一个项目时，它使用d个散列函数来定位d个散列位，并将所有这些位设置为1。当查询一个项时，如果所有d个哈希位都为1，则报告为真;否则，报告false。标准的布隆过滤器只有假阳性错误(false positive errors)，没有假阴性错误(false negative errors)。对于不在集合中的某些项，它可能报告为真，但对于集合中的项，它永远不会报告为假。

​ 多层布隆过滤器:为了在布隆过滤器和CM-CU之间架起桥梁，我们引入了一种新的数据结构，称为多层布隆过滤器(Multi-layer Bloom Filter)，用于估计项目频率。多层布隆过滤器是一个具有相同w, d和哈希函数的标准布隆过滤器数组。每个Bloom过滤器的level等于它在数组中从1到λ的索引。当插入一个项目时，我们检查一级(level-1)布隆过滤器是否报告为真:1)如果报告为假，我们只设置一级布隆过滤器中的d个哈希位为1，插入结束;2)如果报告为真，我们需要检查是否有2级(level-2)Bloom filter报告为真，依靠结果来决定我们是否应该结束插入或继续检查3级(level-3)布隆过滤器。

6. 性能评价(Performance Evaluation)

​ 1)Estimating Item Frequency:比较4种方法：CM、CM-CU、CM-CU with ASketch、和 CM-CU with Cold Filter。

​ 2)Estimating Top-k Hot Items:比较4种方法：CM with heap、CM-CU with heap、Space-Saving、Space-Saving with Cold Filter。

​ 3)Detecting Heavy Changes:比较两种方法：FlowRadar和FlowRadar wiht Cold Filter。

6.1 评价指标(Metrics)

​ 平均绝对误差(AAE):模型预测值 f(x) 与样本真实值 y 之间距离的平均值，表达式为

$AAE=\frac{1}{\psi }{\sum }_{e_i\in \psi }|f_i-\widehat{f_i}|$。

​ 平均相对误差(ARE):ARE被定义为$\frac{1}{|\psi |}{\sum }_{e_i\in \psi }|f_i-\widehat{f_i}|/f_i$。

​ 混淆矩阵：假如现在有一个二分类问题，那么预测结果和实际结果两两结合会出现如下四种情况。

​ 由于用数字1、0表示不太方便阅读，我们转换一下，用T(True)代表正确、F(False)代表错误、P(Positive)代表1、N(Negative)代表0。先看预测结果(P|N)，然后再针对实际结果对比预测结果，给出判断结果(T|F)。按照上面逻辑，重新分配后为

TP、FP、FN、TN可以理解为

• TP：预测为1，实际为1，预测正确。
• FP：预测为1，实际为0，预测错误。
• FN：预测为0，实际为1，预测错误。
• TN：预测为0，实际为0，预测正确。

​ 准确率(Accuracy): 预测正确的结果占总样本的百分比，表达式为$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$。虽然准确率能够判断总的正确率，但是在样本不均衡的情况下，并不能作为很好的指标来衡量结果。

​ 精确率(Precision):又叫查准率，是针对预测结果而言的，其含义是在被所有预测为正的样本中实际为正样本的概率，表达式为 $Precision=\frac{TP}{TP+FP}$，精确率和准确率看上去有些类似，但是是两个完全不同的概念。精确率代表对正样本结果中的预测准确程度，准确率则代表整体的预测准确程度，包括正样本和负样本。

​ 召回率(Recall):又叫查全率，是针对原样本而言的，其含义是在实际为正的样本中被预测为正样本的概率，表达式为$Recall=\frac{TP}{TP+FN}$。

​ F1分数(F1 score): 需要先理解P-R(精确率-召回率曲线)，首先我们先明确目标，我们希望精确率和召回率都很高，但实际上是矛盾的，我们可以根据他们之间的平衡点，定义一个新的指标：F1分数(F1-Score)。F1分数同时考虑精确率和召回率，让两者同时达到最高，取得平衡。F1分数表达式为 $F1-Score=\frac{2\ast Precision\ast Recall}{Precision+Recall}$。

​ 真正率(TPR)=灵敏度(Sensitivity)=TP/(TP+FN)。

​ 假正率(FPR)=1-特异度(Specificity)=FP/(FP+TN)。

​ ROC曲线：如何判断ROC曲线的好坏呢？我们来看，FPR表示模型虚报的程度，TPR表示模型预测覆盖的程度。理所当然的，我们希望虚报的越少越好，覆盖的越多越好。所以TPR越高，同时FPR越低，也就是ROC曲线越陡，那么模型的性能也就越好。

​ AUC(Area Under Curve):表示ROC中曲线下的面积，用于判断模型的优劣。如ROC曲线所示，连接对角线的面积刚好是0.5，对角线的含义也就是随机判断预测结果，正负样本覆盖应该都是50%。另外，ROC曲线越陡越好，所以理想值是1，即正方形。所以AUC的值一般是介于0.5和1之间的。AUC评判标准:面积越大越好。

参考文献:

(1)详解准确率、精确率、召回率、F1值等评价指标的含义-腾讯云开发者社区-腾讯云 (tencent.com)

(2)sklearn计算准确率、精确率、召回率、F1 score_sklearn准确率-CSDN博客

(3)Metric评价指标及损失函数-Error系列之平均绝对误差（Mean Absolute Error，MAE） - 知乎 (zhihu.com)

6.2 对三种关键任务进行评价(Evaluation on Three Key Tasks)

​ 准确性(Accuracy)：结果表明，当Cold Filter内存百分比($M_{cf}/M_t$)设置为90%在两个真实世界数据集中时，使用Cold Filter的CM-CU的AAE分别比CM、CM-CU和使用ASketch的CM- CU的AAE低9.8倍、5.2倍和5.2倍，低12.5倍、7.3倍和7.3倍。

​ 插入速度(Insertion Speed):结果表明，当$M_{cf}/M_t$设置为90%时，使用Cold Filter的CM-CU的插入速度分别比CM、CM-CU和使用ASketch的CM-CU的插入速度快2.5倍、2.9倍和3.4倍，1.6倍、1.7倍和3.4倍。

​ 查询速度(Query Speed):当$M_{cf}/M_t$设置为90%时，使用Cold filter的CM-CU的查询速度分别是CM、CM-CU和使用ASketch的CM-CU的查询速度的1.1倍、1.1倍和1.3倍，1.3倍和1.3倍。

6.3 敏感性分析(Sensitivity Analysis)

​ 1) 纯Cold Filter对提高精度起主要作用，而Aggregate-and-report策略是提高速度的主要因素; 2) CF+Agg+Oma(即Cold Filter + Aggregate-and-report + One-memory access)实现高精度和高速度; 3)对于阈值$\tau$要求较高或者速度相对较慢的流处理算法，在Agg中加入CF可以提高速度。

​ 1)$M_1+M_2$主要影响精度($M_1$是Cold filter第一层使用的内存数量，$M_2$是Cold filter第二层使用的内存数量)，$d_b$主要影响速度($d_b$是哈希函数数量); 2)对于CM-CU, $M_1+M_2$越大，精度越高; 对于SS, $M_1+M_2$对其精度影响不大; 对于FR，相对较小的$M_1+M_2$带来较低的$T_m$。

6.4 Cold Filter参数设置

​ 1)Cold Filter的两层，${\delta }_1:{\delta }_2=4:16$并且有3或4个哈希函数被推荐，可以同时实现高的准确性和高的速度。 2）对于CM-CU,$M_1/(M_1+M_2)$应该在55%到70%范围内；对于SS，$M_1/(M_1+M_2)$应该在35%，$M_1/(M_1+M_2)$对FR的性能有很小的影响。 3）$\tau$对CM-CU和FR的性能有很小的影响。 对于Space-Saving，阈值$\tau$应该被设置根据第$k^{th}$最热项目的预测频率来设置。

7. 总结

​ 我们提出了一个名为Cold Filter的元框架来增强现有的近似流处理算法(approximate stream processing algorithm)。我们的元框架适用于各种流处理任务，同时提高了精度和速度。我们还介绍了如何在三个关键流处理任务上部署它，包括估计项目频率(estimating item frequency)、查找top-k热门项目(finding top-k hot item)和检测重大变化(detecting heavy changes)。实验结果表明，与现有解决方案相比，该方法显著提高了它们的处理速度和精度。我们的Cold Filter元框架可以应用于许多近似的流处理任务(approximate stream processing tasks)，如项目频率分布(distribution of item frequency)、heavy hitter、信息熵(information entropy)等，并提高它们的性能。

8. 可继续学习文献

[1] Pratanu Roy, Arijit Khan, and Gustavo Alonso. Augmented sketch: Faster and more accurate stream processing. In Proc. ACM SIGMOD, pages 1449–1463, 2016.(Augmented Sketch)

[2] Graham Cormode and Marios Hadjieleftheriou. Finding frequent items in data streams. Proc. VLDB, 1(2):1530–1541, 2008.(frequent items)

[3] Ahmed Metwally, Divyakant Agrawal, and Amr El Abbadi. Efficient computation of frequent and top-k elements in data streams. In International Conference on Database Theory, pages 398–412. Springer, 2005.(Space-Saving)

[4] Robert Schweller, Ashish Gupta, Elliot Parsons, and Yan Chen. Reversible sketches for efficient and accurate change detection over network data streams. In Proc. ACM IMC, pages 207–212. ACM, 2004.(Reversible sketch)

[5] Yang Zhou, Peng Liu, Hao Jin, Tong Yang, Shoujiang Dang, and Xiaoming Li. One memory access sketh: a more accurate and faster sketch for per-flow measurement. IEEE Globecom, 2017.(One memory access sketch)

[6] Amit Goyal, Daume, Hal Iii, and Graham Cormode. Sketch algorithms for estimating point queries in nlp. In Proc. EMNLP, 2012.(CM-CU Sketch)

[7] Michael T Goodrich and Michael Mitzenmacher. Invertible bloom lookup tables. In Proceedings of the 49th Annual Allerton Conference on Communication, Control, and Computing, pages 792–799. IEEE, 2011.(Invertible Bloom Lookup Table)

[8] Sumit Ganguly, Minos Garofalakis, and Rajeev Rastogi. Processing data-stream join aggregates using skimmed sketches. In International Conference on Extending Database Technology, pages 569–586. Springer, 2004. (skimmed sketch)

[9] Brian Babcock, Shivnath Babu, Mayur Datar, Rajeev Motwani, and Jennifer Widom. Models and issues in data stream systems. In Proc. ACM PODS, pages 1–16. ACM, 2002.(cash register model)

[10] Gurmeet Singh Manku and Rajeev Motwani. Approximate frequency counts over data streams. In Proc. VLDB, pages 346–357. VLDB Endowment, 2002.(Lossy Counting)

[11] Balachander Krishnamurthy, Subhabrata Sen, Yin Zhang, and Yan Chen. Sketchbased change detection: methods, evaluation, and applications. In Proc. ACM IMC, pages 234–247. ACM, 2003.(The k-ary sketch)

[12] Robert Schweller, Zhichun Li, Yan Chen, et al. Reversible sketches: enabling monitoring and analysis over high-speed data streams. IEEE/ACM ToN, 15(5):1059–1072, 2007.(Reversible sketch)

[13] Burton H Bloom. Space/time trade-offs in hash coding with allowable errors. Communications of the ACM, 13(7):422–426, 1970.(bloom filter)

[14] Haipeng Dai and Muhammad Shahzad and Alex X Liu and Yuankun Zhong. Finding persistent items in data streams. Proceedings of the VLDB Endowment, 289–300, 2016.(persistent items)

[15] Haipeng Dai and Meng Li and Alex X Liu. Finding Persistent Items in Distributed Datasets. IEEE INFOCOM, 2018.(persistent items)
d Muhammad Shahzad and Alex X Liu and Yuankun Zhong. Finding persistent items in data streams. Proceedings of the VLDB Endowment, 289–300, 2016.(persistent items)

[15] Haipeng Dai and Meng Li and Alex X Liu. Finding Persistent Items in Distributed Datasets. IEEE INFOCOM, 2018.(persistent items)