【深度挖掘Java性能调优】「底层技术原理体系」深入挖掘和分析如何提升服务的性能以及执行效率(引导篇)
深入挖掘和分析如何提升服务的性能以及执行效率
- 前提介绍
-
- 知识要点
- 性能概述
-
- 教你看懂程序的性能
-
- 案例介绍
- 性能指标
- 性能的参考指标
- 性能瓶颈(木桶原理)
- 性能分析三大定律
-
- Amdahl定律
-
- 计算公式
-
- 参数解释
- 案例分析
- 定律总结
- Gustafson定律
-
- 与Amdahl定律相对立
- Gustafson的逻辑公式
- Sun-Ni定律
-
- 深入分析Sun-Ni
-
- Sun-Ni定律还强调尽量增大问题规模
- 定律总结
- 课外知识普及
前提介绍
本篇文章全面介绍了性能优化技术,旨在帮助读者了解性能概念以及性能优化的基本思路和方法。通过掌握这些内容,读者将能够对性能问题进行系统分析,提升应用程序的性能。
知识要点
- 评价性能的主要指标
- 木桶原理的概念及其在性能优化中的应用
- Amdahl定律的含义
- 性能调优的层次
- 系统优化的一般步骤和注意事
性能概述
许多人经常会抱怨程序为什么总是那么慢,它到底在干什么?时间都花到哪里去了?这些问题常常让人困扰。如果你也有类似的经历,那么很可能你的程序存在性能问题。相比功能性问题,性能问题有时可能被忽视或将就过去。然而,严重的性能问题有可能导致程序瘫痪、假死甚至崩溃。因此,了解性能的各种表现和指标非常重要。
教你看懂程序的性能
对于客户端程序而言,低劣的性能将严重影响用户体验。用户会不断抱怨界面停顿、抖动、响应迟钝等问题。
案例介绍
- 一个典型的例子是Eclipse IDE,在执行Full GC时会导致程序假死,这一问题被许多开发人员所诟病。对于服务器程序来说,性能问题更加重要,许多后台服务器软件都有自己的性能目标。
- 以Web服务器为例,服务器的响应时间和吞吐量是两个重要的性能指标。当服务器面临巨大的访问压力时,可能会出现响应时间延长、吞吐量下降甚至内存溢出导致崩溃等问题。
上述这两个案例这些都是性能调优需要解决的问题。
性能指标
- 执行速度:程序的反应是否迅速,响应时间是否足够短。
- 内存分配:内存分配是否合理,是否过多消耗内存或存在内存泄漏。
- 启动时间:程序从启动到正常处理业务所需的时间。
- 负载承受能力:当系统承受压力增加时,系统的执行速度和响应时间是否能平稳上升。
性能的参考指标
为了进行科学的性能分析,对性能指标进行定量评估是非常重要的。目前,可以用于定量评估的性能指标包括:
- 执行时间:代码从开始运行到结束所使用的时间。
- CPU占用时间:函数或线程占用CPU的时间。
- 内存分配:程序在运行时所使用的内存空间。
- 磁盘吞吐量:描述磁盘的使用情况。
- 网络吞吐量:描述网络的使用情况。
- 响应时间:系统对某个用户行为或事件做出响应的时间。响应时间越短,性能越好。
处理器(CPU):在需要大量计算的应用中,CPU的处理能力可能成为系统的瓶颈。
内存(RAM):在需要大量数据处理和存储的应用中,内存的容量和速度可能成为系统的瓶颈。
磁盘(硬盘或固态硬盘):在需要频繁进行数据读写的应用中,磁盘的读写速度可能成为系统的瓶颈。
网络带宽:在需要大量数据传输的分布式系统中,网络带宽的限制可能成为系统的瓶颈。
性能瓶颈(木桶原理)
木桶原理又称“短板理论”,其核心思想是:—一只木桶盛水的多少,并不取职决于桶壁上最高的那块木块,而是取决于桶壁上最短的那块,如下图所示:
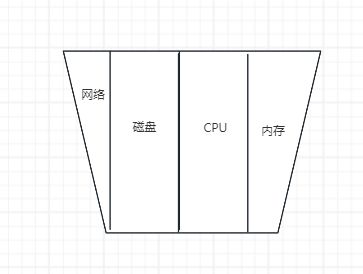
根据木桶原理,一个系统的最终性能受限于其性能最差的组件因此,为了提升系统整体的性能,需要集中精力对性能最差的组件进行优化,而不是将注意力放在性能良好的组件上。这意味着系统的整体性能会受到性能最差组件的制约,只有通过改进和优化这些性能最差的组件,我们才能最大程度地提升系统的性能。因此,在进行性能优化时,我们需要聚焦于系统中最薄弱的环节,以实现整体性能的最大化优化。
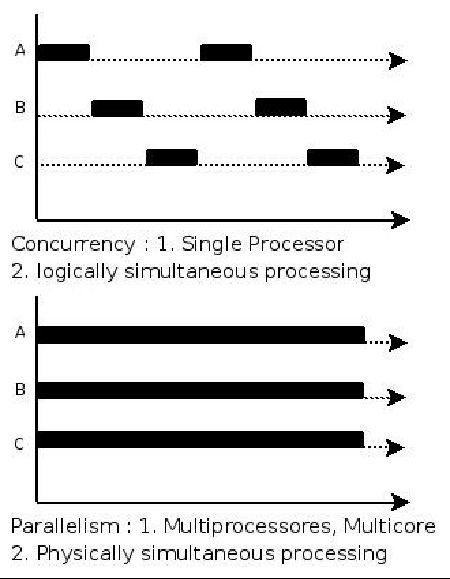
即使系统具有丰富的内存资源和CPU资源,但如果磁盘IO性能低下,那么系统的整体性能将取决于当前最慢的磁盘IO速度,而不是当前最优的CPU或内存。在这种情况下,优化内存或CPU资源是无用的,只有通过提高磁盘IO性能才能对系统的整体性能进行优化。因此,磁盘IO成为系统的性能瓶颈。
性能分析三大定律
Amdahl定律
Amdahl定律以计算机架构师 Gene Amdahl 命名,是并行计算中的一个基本原理,它量化了程序在多个处理器上执行时的潜在速度提升。它有助于深入了解并行化的局限性,并帮助优化并行计算系统的性能。
它主要讨论了加速比(speedup)的问题,推算初整个系统的最大预期改进的最大预期改进。
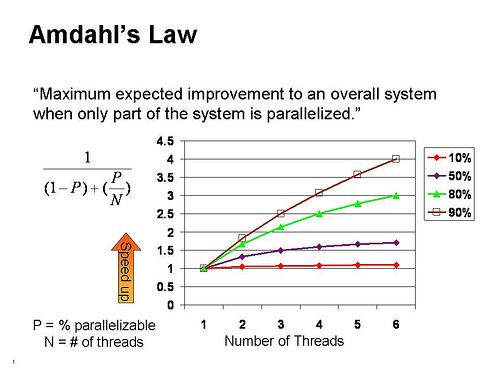
计算公式
Amdahl指出,程序的加速受限于程序中无法并行化的部分。其数学表达式为:
Speedup = 1 / [(1 - P) + (P / N)]
参数解释
- Speedup:是程序并行化后性能的提升。
- P:是可并行化的程序比例。
- N:是用于并行执行的处理器或线程数。
根据Amdahl定律,可实现的最大速度提升与程序中不可并行化的部分成反比。即使有无限多的处理器,速度提升也会受到程序顺序部分的限制。
Amdahl定律强调了识别和优化程序关键顺序部分以实现显著提速的重要性。如果程序中不可并行的部分较多,那么只关注程序的并行化可能不会带来实质性的性能提升。
案例分析
例如,假设一个程序 80% 的代码可以并行化(P = 0.8),如果我们在 10 个处理器(N = 10)上执行这个程序,应用阿姆达尔定律,我们可以计算出最大加速度如下:
加速度 = 1 / [(1 - 0.8) + (0.8 / 10)] 。
= 1 / (0.2 + 0.08)
= 1 / 0.28 ≈ 3.57
上面的结果意味着,即使使用 10 个处理器,我们所能达到的最大速度也比顺序执行快约 3.57 倍。
定律总结
Amdahl定律的重要性在于它提醒我们,如果程序中存在大量的顺序执行部分,即不可并行化的部分,那么即使将其余部分并行化,也无法获得线性的性能提升。
Gustafson定律
Gustafson定律认为随着处理器个数的增加,计算总量可以同时增加,从而实现更高的性能。如果现实情况符合Gustafson定律的假设前提,那么软件的性能将可以随着处理器个数的增加而增加。
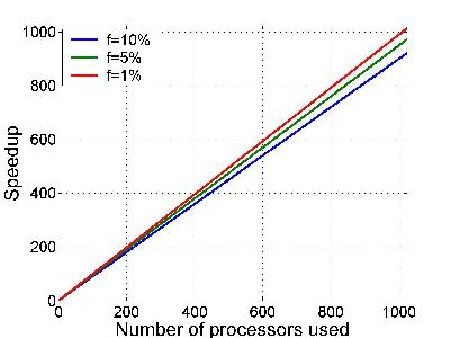
与Amdahl定律相对立
Gustafson假设是与阿姆达尔定律相对的一种观点,它认为随着处理器个数的增加,计算总量可以同时增加,从而实现更高的性能。与阿姆达尔定律关注固定问题规模下的性能提升不同,Gustafson定律关注的是在可扩展问题上的性能提升。
Gustafson的逻辑公式
根据Gustafson定律,加速系数(Speedup)几乎与处理器个数成正比,而不是受到不可并行化部分的限制。这意味着,随着处理器个数的增加,计算总量可以线性地增加,而不是受到串行部分的限制。
speedUp = N * C * M
- N:物理内核数
- C:主频数值
- M:逻辑内核数
一般而言,在实际应用中,需要综合考虑问题的特性和并行化策略,以确定最佳的性能优化方法。
Sun-Ni定律
Sun-Ni定律是一种关于计算资源利用和问题规模的原则,它强调充分利用存储空间等计算资源,并尽量增大问题规模以产生更好和更精确的解决方案。
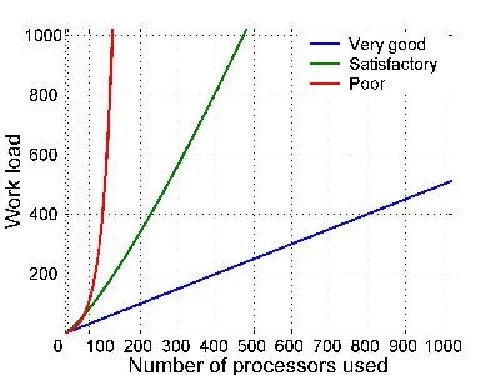
深入分析Sun-Ni
根据Sun-Ni定律,通过充分利用计算资源,特别是存储空间,可以提高问题求解的质量和准确性。存储空间在计算中起着重要的作用,可以用于存储中间结果、数据结构和算法所需的信息等。通过充分利用存储空间,可以提供更多的计算资源来处理问题,从而产生更好的解决方案。
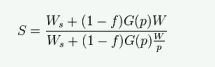
Sun-Ni定律还强调尽量增大问题规模
通过增大问题规模,可以更全面地考虑问题的各个方面,并提供更准确的解决方案。较大的问题规模可以提供更多的数据和信息,使得算法和模型能够更好地捕捉问题的复杂性和细节,从而得到更精确的结果。
定律总结
Sun-Ni定律指出了充分利用存储空间等计算资源,并尽量增大问题规模以产生更好和更精确的解决方案的重要性。通过充分利用计算资源和增大问题规模,可以提高问题求解的质量、准确性和全面性。
课外知识普及
谈到并发技术,不可避免地要提及Doug Lea,他是当今世界上并发程序设计领域的先驱和知名学者。Doug Lea是util.concurrent包的作者,他为并发编程领域做出了突出的贡献,并参与制定了JSR166规范。他的工作对于推动并发编程的发展和实践起到了重要的推动作用。

图书著作《Concurrent Programming in Java: Design Principles and Patterns》以及其两篇论文《A Scalable Elimination-based Exchange Channel》和《Scalable Synchronous Queues》是非阻塞同步算法领域的经典文章。其中,《A Scalable Elimination-based Exchange Channel》和《Scalable Synchronous Queues》论文被公认为非阻塞同步算法的重要篇章。
此外,该著作还有另一个重要影响,即A fork/join framework,这一架构对Java 7的发展产生了深远的影响。