卷积核矩阵矩阵分解闭式解: Convolutional neural networks with low-rank regularization
@inproceedings{tai2015convolutional,
author = {Cheng Tai and
Tong Xiao and
Xiaogang Wang and
Weinan E},
editor = {Yoshua Bengio and
Yann LeCun},
title = {Convolutional neural networks with low-rank regularization},
booktitle = {4th International Conference on Learning Representations, {ICLR} 2016,
San Juan, Puerto Rico, May 2-4, 2016, Conference Track Proceedings},
year = {2016},
url = {http://arxiv.org/abs/1511.06067},
timestamp = {Thu, 15 Apr 2021 16:42:19 +0200},
biburl = {https://dblp.org/rec/journals/corr/TaiXWE15.bib},
bibsource = {dblp computer science bibliography, https://dblp.org}
}
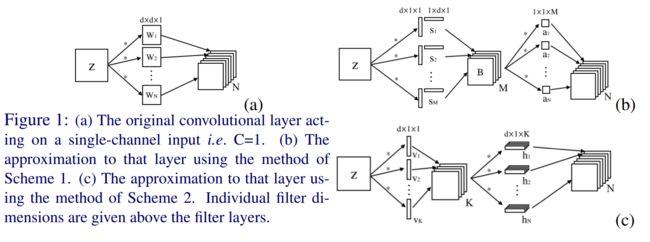
这篇文章给出了一个 s × s s\times s s×s 的卷积核变成 s × 1 s\times 1 s×1 和 1 × s 1\times s 1×s卷积的闭式解,同时引入BN来缓解 retrain 时候梯度爆炸和消失问题.
接下来看下源码与文章的对应关系,他们的源码在:
https://github.com/chengtaipu/lowrankcnn
以VGG每一层的卷积核做矩阵分解为例
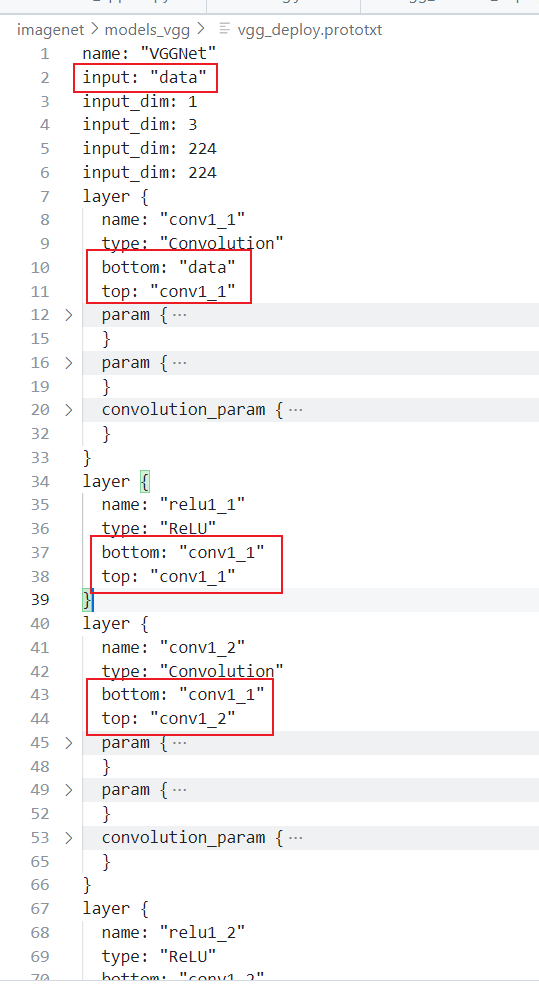
VGG第一层的 .prototxt 文件内容,就是模型网络的拓扑结构用一些键值对的形式来表达
layer {
name: "conv1_1"
type: "Convolution"
bottom: "data"
top: "conv1_1"
param {...}
param {...}
convolution_param {
num_output: 64
pad: 1
kernel_size: 3
weight_filler {
type: "gaussian"
std: 0.059
}
bias_filler {
type: "constant"
value: 0
}
}
}
3 × 3 3\times 3 3×3 的卷积核变成 3 × 1 3\times 1 3×1 和 1 × 3 1\times 3 1×3,不太清楚 3 × 1 3\times 1 3×1 卷积的输出通道是 5 是怎么计算的, 外部有个 conf 文件传入的
layer {
name: "conv1_1_v"
type: "Convolution"
bottom: "data"
top: "conv1_1_v"
param {...}
param {...}
convolution_param {
num_output: 5
weight_filler {
type: "gaussian"
std: 0.059
}
bias_filler {
type: "constant"
value: 0.0
}
pad_h: 1
pad_w: 0
kernel_h: 3
kernel_w: 1
stride_h: 1
stride_w: 1
}
}
layer {
name: "conv1_1_h"
type: "Convolution"
bottom: "conv1_1_v"
top: "conv1_1"
param {...}
param {...}
convolution_param {
num_output: 64
weight_filler {
type: "gaussian"
std: 0.059
}
bias_filler {
type: "constant"
value: 0.0
}
pad_h: 0
pad_w: 1
kernel_h: 1
kernel_w: 3
stride_h: 1
stride_w: 1
}
}
源码的话,比较简单,就是把 s × s s\times s s×s 的卷积核变成 s × 1 s\times 1 s×1 和 1 × s 1\times s 1×s,和上边 prototxt 文件是对应的
def vh_decompose(conv, K):
def _create_new(name):
new_ = LayerParameter()
new_.CopyFrom(conv)
new_.name = name
new_.convolution_param.ClearField('kernel_size')
new_.convolution_param.ClearField('pad')
new_.convolution_param.ClearField('stride')
return new_
conv_param = conv.convolution_param
# vertical
v = _create_new(conv.name + '_v')
del(v.top[:])
v.top.extend([v.name])
v.param[1].lr_mult = 0
v_param = v.convolution_param
v_param.num_output = K
v_param.kernel_h, v_param.kernel_w = conv_param.kernel_size, 1
v_param.pad_h, v_param.pad_w = conv_param.pad, 0
v_param.stride_h, v_param.stride_w = conv_param.stride, 1
# horizontal
h = _create_new(conv.name + '_h')
del(h.bottom[:])
h.bottom.extend(v.top)
h_param = h.convolution_param
h_param.kernel_h, h_param.kernel_w = 1, conv_param.kernel_size
h_param.pad_h, h_param.pad_w = 0, conv_param.pad
h_param.stride_h, h_param.stride_w = 1, conv_param.stride
return v, h
值得一提的是,caffe里每一个层的输入是bottom,输出是top,ReLU 的话,应该是 inplace 操作,所以bottom和 top 的内容是一样的?
下边的代码是重头戏,将一个4d的卷积核参数分解为两个 s × 1 s\times 1 s×1 和 1 × s 1\times s 1×s的卷积核参数
def approx_lowrank_weights(orig_model, orig_weights, conf,
lowrank_model, lowrank_weights):
orig_net = caffe.Net(orig_model, orig_weights, caffe.TEST)
lowrank_net = caffe.Net(lowrank_model, orig_weights, caffe.TEST)
for layer_name in conf:
W, b = [p.data for p in orig_net.params[layer_name]]
v_weights, v_bias = \
[p.data for p in lowrank_net.params[layer_name + '_v']]
h_weights, h_bias = \
[p.data for p in lowrank_net.params[layer_name + '_h']]
# Set biases
v_bias[...] = 0
h_bias[...] = b.copy()
# Get the shapes
num_groups = v_weights.shape[0] // h_weights.shape[1]
N, C, D, D = W.shape
N = N // num_groups
K = h_weights.shape[1]
# SVD approximation
for g in xrange(num_groups):
W_ = W[N*g:N*(g+1)].transpose(1, 2, 3, 0).reshape((C*D, D*N))
U, S, V = np.linalg.svd(W_)
v = U[:, :K] * np.sqrt(S[:K])
v = v[:, :K].reshape((C, D, 1, K)).transpose(3, 0, 1, 2)
v_weights[K*g:K*(g+1)] = v.copy()
h = V[:K, :] * np.sqrt(S)[:K, np.newaxis]
h = h.reshape((K, 1, D, N)).transpose(3, 0, 1, 2)
h_weights[N*g:N*(g+1)] = h.copy()
lowrank_net.save(lowrank_weights)
原文说,下式
E 1 ( H , V ) : = ∑ n , c ∥ W n c − ∑ k = 1 K H n k ( V k c ) T ∥ F 2 E_ {1} (H,V):= \sum _ {n,c} \|W_ {n}^ {c} - \sum _ {k=1}^ {K} H_ {n}^ {k} (V_ {k}^ {c})^ {T} \|_ {F}^ {2} E1(H,V):=n,c∑∥Wnc−k=1∑KHnk(Vkc)T∥F2
的闭式解就是
V ^ k c ( j ) = C ( c − 1 ) d + j , k D k , k H ^ n k ( j ) = C ( n − 1 ) d + j , k D k , k \hat{V}^{c}_{k}(j) = C_{(c-1)d+j, k} \sqrt{D_{k,k}} \\ \hat{H}^{k}_{n}(j) = C_{(n-1)d+j, k} \sqrt{D_{k,k}} V^kc(j)=C(c−1)d+j,kDk,kH^nk(j)=C(n−1)d+j,kDk,k
其中, W = U D Q T W = UDQ^T W=UDQT,是 W W W的SVD
说实话,有点儿不相信,我还以为没有闭式解呢,他原文也说了:
In line with the method in Jaderberg et al. (2014), the proposed tensor decomposition scheme is based on a conceptually simple idea: replace the 4D convolutional kernel with two consecutive kernels with a lower rank.
他们这篇是follow了我前俩篇阅读的文章——用 d × 1 + 1 × d d\times 1+1\times d d×1+1×d去近似 d × d d\times d d×d卷积,那篇用共轭梯度下降法去算一边儿这个优化目标的数值解:
m i n { h n k } , { v k c } ∑ n = 1 N ∑ c = 1 C ∥ W n c − ∑ k = 1 K h n k × v k c ∥ 2 2 min_{ \{h_{n}^{k}\}, \{v_{k}^{c}\} } \sum_{n=1}^{N} \sum_{c=1}^{C} \| W_n^c - \sum_{k=1}^{K} h_{n}^{k} \times v_{k}^{c} \|_{2}^{2} min{hnk},{vkc}n=1∑Nc=1∑C∥Wnc−k=1∑Khnk×vkc∥22