Polygon zkEVM递归证明技术文档（2）—— Polygon zkEVM架构设计

前序博客见：

• Polygon zkEVM递归证明技术文档（1）【主要描述了相关工具 和 证明的组合、递归以及聚合】

本文重点关注Polygon zkEVM的架构设计。

4. Polygon zkEVM

4.1 架构

本节，借助递归、聚合和组合，提供具体的blocks和steps来证明Polygon zkEVM中a batch of transactions（或多个batches）的正确执行。
如之前所属，生成proof分为2个阶段：

• 1）setup阶段：为每个STARK计算定义 仅设置执行一次。setup阶段会预处理生成不同的artifacts，这些artifacts在生成proof时是必须的。
  • 对于Polygon zkEVM场景，相应的STARK计算是指对batches的处理。
• 2）proving阶段：根据输入（即batches of transactions）生成实际的proof。

proving阶段总体架构流程见下图：

注意，首个STARK会生成big proof ${\pi }_{batch}$，该big proof中包含大量的多项式，因此其attached FRI使用low blowup factor，因此：

• 1）Compression Stage：对每个batch proof ${\pi }_{batch}$做压缩变成${\pi }_{c12a}$，其目的是：

  • 减少所用的多项式的数量
  • 支持扩大blowup factor
  • 从而降低proof size。

• 2）Normalization Stage：需要该Normalization Stage的原因在于：

  • 聚合2个proof时需要将前一circuit的constant root用作public input。

  因此Normalization Stage负责将${\pi }_{batch}$ Verifier circuit中的constant root转换public，即${\pi }_{batch}$经Normalization Stage之后，变为了${\pi }_{rec1}$，${\pi }_{rec1}$的Verifier circuit中的constant root是public的。该step使得每个aggregator Verifiers和normalization Verifiers是完全相同的，从而支持通过递归实现聚合：
  

• 3）Aggregation Stage：负责将多个batches proofs （实际是经Normalization Stage之后的${\pi }_{rec1}$）聚合为 一个proof——该proof可一次性证明所有batches proofs。
  不过，Aggregation Stage需设计为，支持已聚合proofs ${\pi }_{rec2}$，或仅仅是已压缩和标准化proofs ${\pi }_{rec1}$。
  
  实际实现方式是构建proof组成的二进制树，依次两两聚合。
  
  可聚合多次，直到剩下一个proof。为此，需创建一个可聚合2个Verifiers的电路（recursive2 Prover），其输入可为：

  • 来自前一Normalization Stage的${\pi }_{rec1}$
  • 或，来自聚合后的${\pi }_{rec2}$

• 4）Final Stage：为递归流程的最后一个STARK step，负责在一个完全不同的有限域内验证${\pi }_{rec2}$ proof。Polygon zkEVM中该完全不同的有限域，是指：bn128椭圆曲线。更准确来说，就是：

  • 负责生成transcript的所有哈希是基于bn128域的
  • 从而所有challenges（以及所有多项式）也都属于新的bn128域

  这么做的原因在于，Final Stage之后的流程中，会基于bn128曲线来生成一个SNARK Groth16 proof。
  Final Stage与之前的stage类似，会为${\pi }_{rec2}$实例化一个Verifier circuit，只不过，需提供2个constants roots（分别对应前一step所聚合的proof的constant root）。

• 5）SNARK Stage：整个流程的最后一步，旨在为 验证前面的${\pi }_{recf}$ proof 生成Groth16 proof ${\pi }_{groth16}$。事实上，可将Groth16替换为任何其它SNARK proof。此处选择SNARK的目的在于：

  • 降低验证复杂度
  • 降低proof size：不同于STARK proofs，Groth16 proof具有常量复杂度。

  将${\pi }_{groth16}$ proof发送给Verifier验证。

需注意的是，会将整个public inputs集合 作为 整个递归流程中每个proof的输入。整个public inputs集合为：【详情见 Polygon zkEVM bridge技术文档 和 Polygon zkEVM Trustless L2 State Management 技术文档】

• oldStateRoot
• oldAccInputHash
• oldBatchNum
• chainId
• midStateRoot
• midAccInputHash
• midBatchNum
• newStateRoot
• newAccInputHash
• localExitRoot
• newBatchNum

4.2 Setup阶段

setup阶段为预处理阶段，会创建声称proofs所需的所有artifacts——包括：

• 生成中间电路：有电路的有限集合，支持proof递归和proof集合 的任意组合。

4.2.1 Build the zkEVM STARK——用于生成batch proof ${\pi }_{batch}$

如上图所示：

• 1）build rom 流程：为构建zkEVM状态机的ROM rom.json。ROM程序中包含executor运行的指令，以生成zkEVM的execution trace。
• 2）build pil 流程：生成验证execution trace的PIL zkevm.pil。
• 3）build constants 流程：生成zkEVM execution trace中的所有constant值。其输入有：rom.json、zkevm.starkstruct、zkevm.pil，输出为rom.const。之前也提到过，setup阶段无需committed polynomials，所以此时也不需要运行zkEVM executor来生成committed polynomials。
• 4）build constants tree 流程：输入为rom.const（constant polynomials的evaluations值），输出为：
  • 由此构建的Merkle tree zkevm.consttree。
  • Merkle tree zkevm.consttree的root zkevm.verkey（constRoot）。该root值为对计算中所有固定参数的密码学总结，为哈希值。
• 5）generate starkInfo 流程为：输入有zkevm.starkstruct和zkevm.pil，输出为zkEVM.starkinfo——为自动生成“验证zkEVM STARK”电路所需的starkInfo。

Polygon zkEVM方案在本build阶段时，设置：

• blowup factor为2
• query次数为128

生成proofs需用到上图灰色的artifacts（zkevm.pil、rom.const、zkEVM.starkinfo、zkevm.consttree）。（详细的proof生成细节见4.3节）

4.2.2 Setup S2C for the zkEVM STARK——Compression Stage part1

Setup S2C for the zkEVM STARK——Compression Stage part1的目的在于：

• 为验证zkEVM STARK生成电路

其中：

• 1）pil2circom 流程：会向名为stark_verifier.circom.ejs的EJS模板中，注入 验证zkEVM STARK 所需的所有信息。其输入有：

  • zkevm.pil：以获取多项式名
  • zkevm.starkinfo：定义了blowup factor、query次数、以及FRI验证流程的steps
  • zkevm.verkey（constRoot）：其中的constRoot用于自动生成Circom电路。

  其输出为：Circom文件zkevm.verifier.circom。

• 2）compile circom 流程：Circom文件zkevm.verifier.circom 编译为 R1CS约束系统 zkevm.verifier.r1cs——该约束将后续用于生成下一个proof的PIL和constant polynomials。
  除此之外，compile circom 流程还会输出：

  • zkevm.verifier.witnesscalc：为witness calculator程序，上图中将其标记为灰色，是因为需将其用于proof生成。

4.2.3 Setup C2S c12a——Compression Stage part2

Compression Stage的目的是降低proof size，因此，需将build时的“blowup factor 2和query次数128” 修改为 “blowup factor 4和query次数64”，该信息见proverjs repo中的c12a.starkstruct文件。

验证zkEVM STARK的电路称为zkevm.verifier Circom电路（或c12a PIL电路）。原因在于：

• 为实现压缩，验证zkevm.verifier Circom电路 的电路为PIL电路c12a ，该PIL电路为PlonKish电路，具有定制门和12个多项式。

其中：

• 1）c12a setup 流程：对应名为compressor12_setup的服务。
  其输入为：

  • 前一验证电路的R1CS描述 zkevm.verifier.r1cs

  输出有：

  • c12a.pil：为machine-like construction，其正确执行，等价为，前一电路的有效性。
  • c12a.const：为定义c12a.pil的所有constant polynomials。
  • c12a.exec：为helper文件。包含了 shuffle所有witness值 所需的所有规则，后续会计算到execution trace的相应位置中。
    该shuffle设计，与，在constant polynomials c12a.const 中定义的connections，一起，对于honest Prover，只要前一电路有效，则新生成的execution trace也是有效的。

• 2）Build c12a constants tree 流程：
  输入有：

  • c12a.const：
  • c12a.starkstruct：具有所有FRI相关参数（其中“blowup factor为4和query次数为64”）

  输出有：

  • c12a.constTree：为constants Merkle tree
  • c12a.verkey（constRoot）：为constants Merkle tree的root

• 3）generate c12a strakInfo 流程：对应generate_starkinfo服务。
  输入有：

  • c12a.starkstruct：
  • c12a.pil：

  输出为：c12a.strarkinfo。

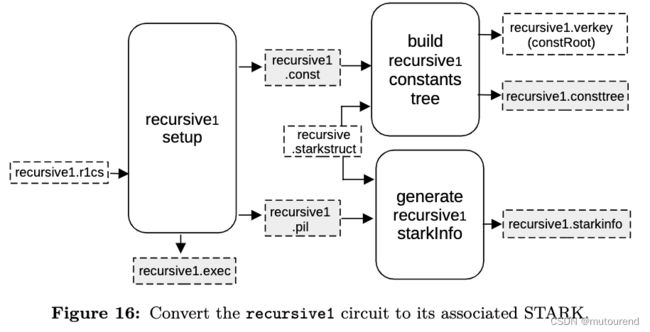
4.2.4 Setup S2C for recursive1——Normalization Stage part1

截止目前，有验证首个big STARK proof ${\pi }_{batch}$的STARK proof ${\pi }_{c12a}$。

接下来的思路，就是为 验证${\pi }_{c12a}$ 生成Circom电路，来模拟FRI验证流程。

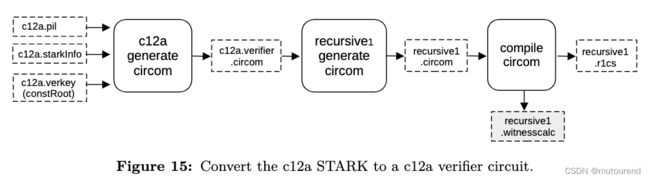
其中：

• 1）c12a generate circom 流程：输入有之前的c12a.pil文件、c12a.starkInfo文件和constant root c12a.verkey（constRoot），与之前类似，通过向stark_verifier.circom.ejs模板注入来生成verifier circuit c12a.verifier.circom。

• 2）recursive1 generate circom 流程：为实现normalization，需要修改verifier circuit c12a.verifier.circom，使得constant root为public input。此时还未聚合，此处实际并未用到该constant root。不过让constant root称为public input，对于后续Aggregation Stage至关重要。因为Aggregation Stage中前一电路计算中所有constants，都必须作为public inputs。
  其输入为verifier circuit c12a.verifier.circom，输出为recursive1.circom（即，将verifier circuit c12a.verifier.circom 实例化在 recursive1.circom 中，连接所有所需的wires，并将constant root放入publics set中）。

• 3）compile circom 流程：将circom文件recursive1.circom 编译为：

  • R1CS文件recursive1.r1cs
  • 和 witness calculator程序 recursive1.witnesscalc

  这2个输出后续用于构建和注入下一execution trace。

4.2.5 Setup C2S for recursive1——Normalization Stage part2

其中：

• 1）recursive1 setup 流程：
  其输入为：

  • recursive1.r1cs：前一验证电路的R1CS描述

  输出有：

  • recursive1.pil：为machine-like construction，其正确执行，等价为，前一电路的有效性。
  • recursive1.const：定义recursive1.pil的所有constant polynomials的值。
  • recursive1.exec：为helper文件，提供了execution trace中相应位置witness值。

• 2）generate recursive1 starkInfo 流程：
  其输入有：

  • recursive1.pil：为machine-like construction，其正确执行，等价为，前一电路的有效性。
  • recursive.starkstruct：存储了本步骤要用到的所有FRI相关参数。【注意，此时的blowup factor 为$2^4=16$，query次数为32。】

  输出有：

  • recursive1.starkinfo：通过generate_starkinfo 服务生成。

• 3）build recursive1 constants tree 流程：
  其输入有：

  • recursive1.const：定义recursive1.pil的所有constant polynomials的值。
  • recursive.starkstruct：存储了本步骤要用到的所有FRI相关参数。【注意，此时的blowup factor 为$2^4=16$，query次数为32。】

  输出有：

  • recursive1.consttree：为constants Merkle tree。
  • recursive1.verkey（constRoot）：为constants Merkle tree的root。

4.2.6 Setup S2C for recursive2——Aggregation Stage part1

目前为止，已有STARK proof ${\pi }_{rec1}$来验证proof ${\pi }_{c12a}$。之前“4.2.4 Setup S2C for recursive1——Normalization Stage part1” 中，通过模拟验证${\pi }_{rec1}$中的FRI验证流程 来生成Circom电路。本节采用类似的方式：

其中：

• 1）recursive1 generate circom 流程：输入有之前的recursive1.pil文件、recursive1.starkInfo文件和constant root recursive1.verkey（constRoot），与之前类似，通过向stark_verifier.circom.ejs模板注入来生成verifier circuit recursive1.verifier.circom。

• 2）recursive2 generate circom 流程：不过与之前“4.2.4 Setup S2C for recursive1——Normalization Stage part1” 不同之处在于：

  • 在stark_verifier.circom.ejs模板生成verifier circuit recursive1.verifier.circom之后，还需要使用另一模板来创建聚合2个Verifiers的Cirom电路。

  • 之前“4.2.4 Setup S2C for recursive1——Normalization Stage part1” 中的constant root是通过外部文件传入硬编码在电路中的——这样做的目标是为实现normalization目的，以 支持在本步骤中所验证的每个proof具有相同的格式，从而使得recursion成为可能。

  • recursive2 generate circom 流程 输出的recursive2.circom电路具有2个Verifiers，有2个multiplexors来实际绝对每个Verifier的格式：

    • 若该proof为${\pi }_{rec1}$格式，则硬编码的constant root为public input；
    • 若该proof为${\pi }_{rec2}$格式，则constant root用作input signal，其源自前一电路。

    所生成的recursive2.circom电路方案示意见下图：
    

  • 若upper proof为${\pi }_{rec2}$格式：则Multiplexor不会将constant root rootC 提供给Verifier A进行硬编码，因为Verifier A应通过前一电路的public input来获取。

  • 若lower proof为${\pi }_{rec1}$格式：则在做相应模板注入时，Multiplexor会将constant root rootC 提供给Verifier B进行硬编码。

• 3）compile circom 流程：通过运行名为genrecursive的不同脚本，将circom文件recursive2.circom 编译为：

  • R1CS文件recursive2.r1cs
  • 和 witness calculator程序 recursive2.witnesscalc

  这2个输出后续用于构建和注入下一execution trace。

4.2.7 Setup C2S for recursive2——Aggregation Stage part2

其中：

• 1）recursive2 setup 流程：
  其输入为：

  • recursive2.r1cs：前一验证电路的R1CS描述

  输出有：

  • recursive2.pil：为machine-like construction，其正确执行，等价为，前一电路的有效性。
  • recursive2.const：定义recursive2.pil的所有constant polynomials的值。
  • recursive2.exec：为helper文件，提供了execution trace中相应位置witness值。

• 2）generate recursive2 starkInfo 流程：
  其输入有：

  • recursive2.pil：为machine-like construction，其正确执行，等价为，前一电路的有效性。
  • recursive.starkstruct：存储了本步骤要用到的所有FRI相关参数。【注意，此时的blowup factor 为$2^4=16$，query次数为32。即，Aggregation Stage与Normalization Stage具有完全相同的参数。】

  输出有：

  • recursive2.starkinfo：通过generate_starkinfo 服务生成。

• 3）build recursive2 constants tree 流程：
  其输入有：

  • recursive2.const：定义recursive2.pil的所有constant polynomials的值。
  • recursive.starkstruct：存储了本步骤要用到的所有FRI相关参数。【注意，此时的blowup factor 为$2^4=16$，query次数为32。即，Aggregation Stage与Normalization Stage具有完全相同的参数。】

  输出有：

  • recursive2.consttree：为constants Merkle tree。
  • recursive2.verkey（constRoot）：为constants Merkle tree的root。

4.2.8 Setup S2C for recursivef——Final Stage part1

截止目前，有STARK proof ${\pi }_{rec2}$ 来验证 另一STARK proof ${\pi }_{rec2}$（或${\pi }_{rec1}$）。

接下来的思路，就是为 验证${\pi }_{rec2}$（或${\pi }_{rec1}$，若实际未聚合） 生成Circom电路，来模拟FRI验证流程。

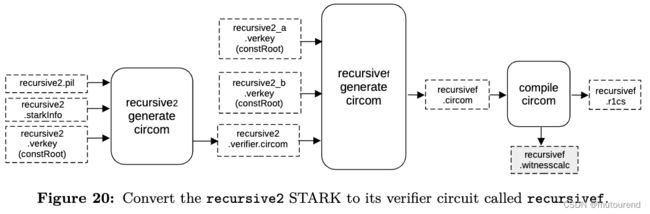
其中：

• 1）recursive2 generate circom 流程：输入有之前的recursive2.pil文件、recursive2.starkInfo文件和constant root recursive2.verkey（constRoot），与之前类似，通过向stark_verifier.circom.ejs模板注入来生成verifier circuit recursive2.verifier.circom。

• 2）recursive2 generate circom 流程：输入有 recursive2.verifier.circom，以及前2个proof的constant roots recursive2_a.verkey.constRoot 和 recursive2_b.verkey.constRoot，通过向stark_verifier.circom.ejs模板注入获得recursivef.circom。

• 3）compile circom 流程：通过运行另一名为genrecursivef的脚本，将circom文件recursivef.circom 编译为：

  • R1CS文件recursivef.r1cs
  • 和 witness calculator程序 recursivef.witnesscalc

  这2个输出后续用于构建和注入下一execution trace。

4.2.9 Setup C2S for recursivef——Final Stage part2

其中：

• 1）recursivef setup 流程：
  其输入为：

  • recursivef.r1cs：前一验证电路的R1CS描述

  输出有：

  • recursivef.pil：为machine-like construction，其正确执行，等价为，前一电路的有效性。
  • recursivef.const：定义recursivef.pil的所有constant polynomials的值。
  • recursivef.exec：为helper文件，提供了execution trace中相应位置witness值。

• 2）generate recursivef starkInfo 流程：运行generate_starkinfo服务。
  其输入有：

  • recursivef.pil：为machine-like construction，其正确执行，等价为，前一电路的有效性。
  • recursivef.starkstruct：存储了本步骤要用到的所有FRI相关参数。【注意，此时的blowup factor 为$2^4=16$，query次数为32。即，Final Stage、Aggregation Stage与Normalization Stage具有完全相同的参数。 】

  输出有：

  • recursivef.starkinfo：通过generate_starkinfo 服务生成。

• 3）build recursivef constants tree 流程：
  其输入有：

  • recursivef.const：定义recursive2.pil的所有constant polynomials的值。
  • recursivef.starkstruct：存储了本步骤要用到的所有FRI相关参数。【注意，此时的blowup factor 为$2^4=16$，query次数为32。即，Final Stage、Aggregation Stage与Normalization Stage具有完全相同的参数。 】

  输出有：

  • recursivef.consttree：为constants Merkle tree。
  • recursivef.verkey（constRoot）：为constants Merkle tree的root。

4.2.10 Setup S2C for final——SNARK Stage

截止目前，有STARK proof ${\pi }_{recf}$ 来验证 另一STARK proof ${\pi }_{rec2}$。

接下来的思路，就是为 验证${\pi }_{recf}$ 生成Circom电路，来模拟FRI验证流程。

其中：

• 1）recursivef generate circom 流程：输入有之前的recursivef.pil文件、recursivef.starkInfo文件和constant root recursivef.verkey（constRoot），与之前类似，通过向stark_verifier.circom.ejs模板注入来生成verifier circuit recursivef.verifier.circom。

• 2）final generate circom 流程：输入有 recursivef.verifier.circom，通过向stark_verifier.circom.ejs模板注入获得final.circom。

• 3）compile circom 流程：将circom文件final.circom 编译为：

  • R1CS文件final.r1cs
  • 和 witness calculator程序 final.witnesscalc

  这2个输出后续用于构建Groth16证明。

4.3 Proof Generation Phase

整个proof生成分为6大阶段：

• 1）生成zkEVM STARK proof ${\pi }_{batch}$
• 2）生成c12a STARK proof ${\pi }_{c12a}$——Compression Stage
• 3）生成recursive1 STARK proof ${\pi }_{rec1}$——Normalization Stage
• 4）生成recursive2 STARK proof ${\pi }_{rec2}$——Aggregation Stage
• 5）生成recursivef STARK proof ${\pi }_{recf}$——Final Stage
• 6）生成final SNARK proof ${\pi }_{groth16}$——SNARK Stage

4.3.1 生成zkEVM STARK proof ${\pi }_{batch}$

其中：

• 1）zkEVM executor 流程：根据zkevm.inputs、zkevm.pil、rom.json来生成execution trace zkevm.commit、zkevm.const、zkevm.constTree。
• 2）stark prover 流程：根据zkevm.commit、zkevm.const、zkevm.constTree、zkevm.pil、zkevm.starkinfo来生成 STARK proof zkevm.proof、zkevm.public、zkevm.zkin.proof（包含了STARK proof和相应的public inputs）。

生成zkEVM STARK proof ${\pi }_{batch}$时的blowup factor为2，因此${\pi }_{batch}$很大，具有大量的多项式。为此，需要后续的c12a 压缩步骤，通过增大blowup factor 来 减少多项式数量。

生成zkEVM STARK proof ${\pi }_{batch}$ 不同于后续的步骤，为递归的开始准备阶段。不过，为统一代码风格，Main Prover流程对证明过程做了抽象，使得后续递归中的每个步骤看起来都是一样的。

4.3.2 生成c12a STARK proof ${\pi }_{c12a}$——Compression Stage

为验证之前的big STARK proof ${\pi }_{batch}$ 生成新的压缩版 STARK proof ${\pi }_{c12a}$。

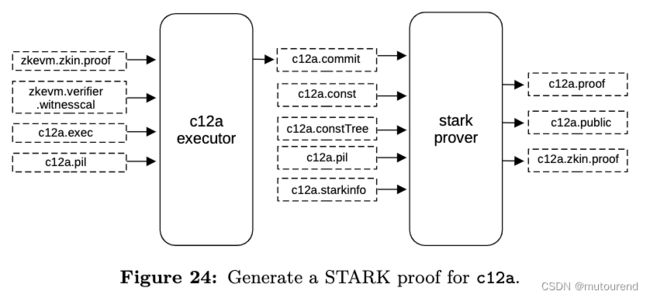
4.3.3 生成recursive1 STARK proof ${\pi }_{rec1}$——Normalization Stage

为 验证之前的STARK proof ${\pi }_{c12a}$ 生成新的normalized STARK proof ${\pi }_{rec1}$。

4.3.4 生成recursive2 STARK proof ${\pi }_{rec2}$——Aggregation Stage

为 验证之前的2个STARK proof ${\pi }_{rec1}$（和${\pi }_{rec2}$） 生成聚合STARK proof ${\pi }_{rec2}$。

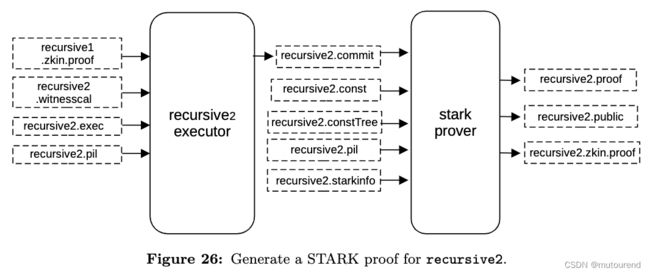
4.3.5 生成recursivef STARK proof ${\pi }_{recf}$——Final Stage

为 验证之前的聚合STARK proof ${\pi }_{rec2}$ 生成新的STARK proof ${\pi }_{recf}$。

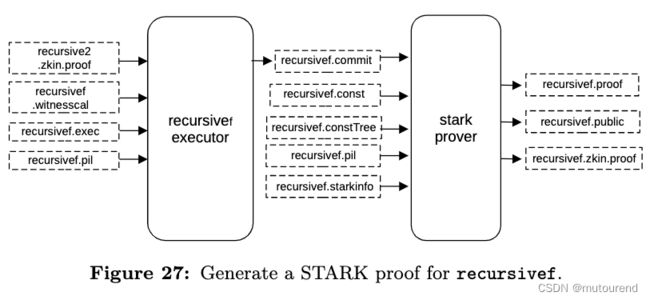
4.3.6 生成final SNARK proof ${\pi }_{groth16}$——SNARK Stage

为 验证${\pi }_{recf}$，使用 递归流程的最后一个电路——final.circom 来生成SNARK proof ${\pi }_{groth16}$。

参考资料

[1] Polygon zkEVM技术文档 Recursion, aggregation and composition of proofs v.1.1

附录：Polygon Hermez 2.0 zkEVM系列博客

• ZK-Rollups工作原理
• Polygon zkEVM——Hermez 2.0简介
• Polygon zkEVM网络节点
• Polygon zkEVM 基本概念
• Polygon zkEVM Prover
• Polygon zkEVM工具——PIL和CIRCOM
• Polygon zkEVM节点代码解析
• Polygon zkEVM的pil-stark Fibonacci状态机初体验
• Polygon zkEVM的pil-stark Fibonacci状态机代码解析
• Polygon zkEVM PIL编译器——pilcom 代码解析
• Polygon zkEVM Arithmetic状态机
• Polygon zkEVM中的常量多项式
• Polygon zkEVM Binary状态机
• Polygon zkEVM Memory状态机
• Polygon zkEVM Memory Align状态机
• Polygon zkEVM zkASM编译器——zkasmcom
• Polygon zkEVM哈希状态机——Keccak-256和Poseidon
• Polygon zkEVM zkASM语法
• Polygon zkEVM可验证计算简单状态机示例
• Polygon zkEVM zkASM 与 以太坊虚拟机opcode 对应集合
• Polygon zkEVM zkROM代码解析（1）
• Polygon zkEVM zkASM中的函数集合
• Polygon zkEVM zkROM代码解析（2）
• Polygon zkEVM zkROM代码解析（3）
• Polygon zkEVM公式梳理
• Polygon zkEVM中的Merkle tree
• Polygon zkEVM中Goldilocks域元素circom约束
• Polygon zkEVM Merkle tree的circom约束
• Polygon zkEVM FFT和多项式evaluate计算的circom约束
• Polygon zkEVM R1CS与Plonk电路转换
• Polygon zkEVM中的子约束系统
• Polygon zkEVM交易解析
• Polygon zkEVM 审计及递归证明
• Polygon zkEVM发布公开测试网2.0
• Polygon zkEVM测试集——创建合约交易
• Polygon zkEVM中的Recursive STARKs
• Polygon zkEVM的gas定价
• Polygon zkEVM zkProver基本设计原则 以及 Storage状态机
• Polygon zkEVM bridge技术文档
• Polygon zkEVM Trustless L2 State Management 技术文档
• Polygon zkEVM中的自定义errors
• Polygon zkEVM RPC服务
• Polygon zkEVM Prover的 RPC功能
• Polygon zkEVM PIL技术文档
• Polygon zkEVM递归证明技术文档（1）