Polygon zkEVM递归证明技术文档(4)—— C12 PIL Description
前序博客有:
- Polygon zkEVM递归证明技术文档(1)【主要描述了相关工具 和 证明的组合、递归以及聚合】
- Polygon zkEVM递归证明技术文档(2)—— Polygon zkEVM架构设计
- Polygon zkEVM递归证明技术文档(3)——代码编译及运行
6. C12 PIL Description
之前,已提供了c12算术化的高层功能概览,并标识了其通用属性以及某些PIL细节。
本节的主要目标是:
- 提供,FRI协议中生成和约束验证流程execution trace中,c12 PIL算术化的详细解释。
6.1 由R1CS到Plonk
之前已提及,验证STARK proof的验证流程是以circom编写的。该流程负责构建一组R1CS(Rank-1 Constraint System)约束。此外,由于circom中无法直接检查定制gates,且.r1cs文件仅包含了关于其输入和输出的计算信息。为引入定制gates,需在所生成的(描述Verifier验证流程的)pil代码中明确指出对定制gates的验证流程。该pil代码将负责嵌入对定制gates所需的验证,以确保其在整个验证流程中功能正常。
不同于Plonk约束,没有直接的方式来将r1cs约束,转换为,具有固定列的(和pil约束集的)execution trace。因此,有必要先将r1cs约束转换为Plonk约束。
回顾下,基于signals集 s 1 , ⋯ , s n s_1,\cdots,s_n s1,⋯,sn的 m m m-维 R1CS,其有3个矩阵 A = ( a i , j ) , B = ( b i , j ) , C = ( c i , j ) A=(a_{i,j}),B=(b_{i,j}),C=(c_{i,j}) A=(ai,j),B=(bi,j),C=(ci,j),对应的矩阵空间为 M ( m , n , F ) M(m,n,\mathbb{F}) M(m,n,F),其中 F \mathbb{F} F对应底层域。当且仅当 A s ∘ B s = C s As\circ Bs=Cs As∘Bs=Cs,可认为 s = ( s 1 , ⋯ , s n ) s=(s_1,\cdots,s_n) s=(s1,⋯,sn) satisfy 该R1CS约束。其中 ∘ \circ ∘表示Hadamard product(或component-wise multiplication)。更具体来说,若 s = ( s 1 , ⋯ , s n ) s=(s_1,\cdots,s_n) s=(s1,⋯,sn) satisfy 该R1CS约束,当且仅当:
( a 1 , 1 s 1 + ⋯ + a 1 , n s n ) ⋅ ( b 1 , 1 s 1 + ⋯ + b 1 , n s n ) = c 1 , 1 s 1 + ⋯ + c 1 , n s n (a_{1,1}s_1+\cdots+a_{1,n}s_n)\cdot (b_{1,1}s_1+\cdots+b_{1,n}s_n)=c_{1,1}s_1+\cdots+c_{1,n}s_n (a1,1s1+⋯+a1,nsn)⋅(b1,1s1+⋯+b1,nsn)=c1,1s1+⋯+c1,nsn
⋯ \cdots ⋯
( a m , 1 s 1 + ⋯ + a m , n s n ) ⋅ ( b m , 1 s 1 + ⋯ + b m , n s n ) = c m , 1 s 1 + ⋯ + c m , n s n (a_{m,1}s_1+\cdots+a_{m,n}s_n)\cdot (b_{m,1}s_1+\cdots+b_{m,n}s_n)=c_{m,1}s_1+\cdots+c_{m,n}s_n (am,1s1+⋯+am,nsn)⋅(bm,1s1+⋯+bm,nsn)=cm,1s1+⋯+cm,nsn
由此可知,以上R1CS公式中不支持 ( 1 + s 2 ) ⋅ s 3 = s 4 (1+s_2)\cdot s_3=s_4 (1+s2)⋅s3=s4这样的约束。为解决在约束中引入常量值的问题,将signal s 1 s_1 s1的值固定为 1 1 1。
可将R1CS约束看成是具有无限fan-in和无限fan-out的gates:
- 无限fan-in:是指可具有任意数量的input wires。
- 无限fan-out:是指可具有任意数量的output wires。
而Plonk约束可看成是具有2个固定fan-in和1个固定fan-out的gates:
- 2个固定fan-in:是指每个Plonk gate都正好有2个input wires。
- 1个固定fan-out:是指每个Plonk gate都正好有1个output wire。
单个Plonk gate由:
- 2个input signals a , b a,b a,b
- 1个output signal c c c
- 5个selectors q R , q L , q M , q O , q C q_R,q_L,q_M,q_O,q_C qR,qL,qM,qO,qC
组成。tuple ( a , b , c ) (a,b,c) (a,b,c) satisfy the Plonk gate,当且仅当:
q R ⋅ a + q L ⋅ b + q M ⋅ a ⋅ b + q O ⋅ c + q C = 0 q_R\cdot a+q_L\cdot b+q_M\cdot a\cdot b+q_O\cdot c+q_C=0 qR⋅a+qL⋅b+qM⋅a⋅b+qO⋅c+qC=0
将R1CS约束转换为Plonk约束的过程为:
- 将每个R1CS约束,映射为1个或多个Plonk约束。
为确保转换正确、优化且易理解的转换,可分不同情况。每种情况,都会定义特定的rules和mappings,来将r1cs约束转换为合适的Plonk约束。具体的规则需考虑所包含的变量类型、所执行的运算、以及最终Plonk约束应满足的属性。所有的策略为,减少 加法求和约束 和 变量,即:
- 对于具有 n − 1 n-1 n−1个非常量项的线性组合 a 1 + a 2 s 2 + ⋯ a n s n a_1+a_2s_2+\cdots a_ns_n a1+a2s2+⋯ansn,可将其reduce为:包含 n − 2 n-2 n−2个非常量项,加,另一artificial signal v 1 v_1 v1的线性组合;和,约束 a n − 1 s n − 1 + a n s n = v 1 a_{n-1}s_{n-1}+a_ns_n=v_1 an−1sn−1+ansn=v1,对应Plonk selectors q L = − a n − 1 , q R = − a n , q M = 0 , q O = 1 , q C = 0 q_L=-a_{n-1},q_R=-a_n,q_M=0,q_O=1,q_C=0 qL=−an−1,qR=−an,qM=0,qO=1,qC=0。从而获得新的reduced线性组合 a 1 + a 2 s 2 + ⋯ + v 1 a_1+a_2s_2+\cdots +v_1 a1+a2s2+⋯+v1。
- 持续以上策略,最终可获得只具有2项 a 1 + v T a a_1+v_{T_a} a1+vTa的reduced线性组合,其中 T a T_a Ta表示所有新加变量的总数。
针对不同情况的完整策略为:
- 1)当R1CS约束中 A = 0 A=0 A=0且(或) B = 0 B=0 B=0时,具有形如:
c 1 + c 2 s 2 + ⋯ + c n s n = 0 c_1+c_2s_2+\cdots +c_ns_n=0 c1+c2s2+⋯+cnsn=0
的线性约束。采用上面的reduction 策略,将其reduce为仅有4项的加法运算(其中1项为常量,另外3项为非常量)。即,最终reduced约束形如:
c 1 + c 2 s 2 + c 3 s 3 + v T = 0 c_1+c_2s_2+c_3s_3+v_T=0 c1+c2s2+c3s3+vT=0
其中 T T T表示新引入的signals总数。此时,可将如上R1CS约束转换为Plonk约束,其中 q R = c 2 , q L = c 3 , q M = 0 , q O = 1 , q C = c 1 q_R=c_2,q_L=c_3,q_M=0,q_O=1,q_C=c_1 qR=c2,qL=c3,qM=0,qO=1,qC=c1。 - 2)当R1CS约束中有 i ≠ 1 , a i = 0 i\neq 1,a_i=0 i=1,ai=0时(其中 a 1 ≠ 0 a_1\neq 0 a1=0为constant wire),对应的线性约束形如:
a 1 ⋅ ( b 1 + b 2 s 2 + ⋯ + b n s n ) = c 1 + c 2 s 2 + ⋯ + c n s n a_1\cdot (b_1+b_2s_2+\cdots+b_ns_n)=c_1+c_2s_2+\cdots+c_ns_n a1⋅(b1+b2s2+⋯+bnsn)=c1+c2s2+⋯+cnsn
此时,相应的策略是:
a 1 ⋅ ( b 1 + b 2 s 2 + ⋯ + b n s n ) = c 1 + c 2 s 2 + ⋯ + c n s n ⇔ a_1\cdot (b_1+b_2s_2+\cdots+b_ns_n)=c_1+c_2s_2+\cdots+c_ns_n \Leftrightarrow a1⋅(b1+b2s2+⋯+bnsn)=c1+c2s2+⋯+cnsn⇔
a 1 b 1 + a 1 b 2 s 2 + ⋯ + a 1 b n s n = c 1 + c 2 s 2 + ⋯ + c n s n ⇔ a_1b_1+a_1b_2s_2+\cdots+a_1b_ns_n=c_1+c_2s_2+\cdots+c_ns_n \Leftrightarrow a1b1+a1b2s2+⋯+a1bnsn=c1+c2s2+⋯+cnsn⇔
a 1 b 1 + a 1 b 2 s 2 + ⋯ + a 1 b n s n − c 1 − c 2 s 2 − ⋯ − c n s n = 0 a_1b_1+a_1b_2s_2+\cdots+a_1b_ns_n-c_1-c_2s_2-\cdots-c_ns_n=0 a1b1+a1b2s2+⋯+a1bnsn−c1−c2s2−⋯−cnsn=0
采用相同的reduction 策略,将其reduce为仅有4项的加法运算(其中1项为常量,另外3项为非常量)。即,最终reduced约束形如:
a 1 b 1 + a 1 b 2 s 2 + a 1 b 3 s 3 + a 1 v T = 0 a_1b_1+a_1b_2s_2+a_1b_3s_3+a_1v_T=0 a1b1+a1b2s2+a1b3s3+a1vT=0
其中 T T T表示新引入的signals总数。此时,可将如上R1CS约束转换为Plonk约束,其中 q R = a 1 b 2 , q L = a 1 b 3 , q M = 0 , q O = a 1 , q C = a 1 b 1 q_R=a_1b_2,q_L=a_1b_3,q_M=0,q_O=a_1,q_C=a_1b_1 qR=a1b2,qL=a1b3,qM=0,qO=a1,qC=a1b1。 - 3)当R1CS约束中有 i ≠ 1 , b i = 0 i\neq 1,b_i=0 i=1,bi=0时(其中 b 1 ≠ 0 b_1\neq 0 b1=0为constant wire),对应的线性约束形如:
( a 1 + a 2 s 2 + ⋯ + a n s n ) ⋅ b 1 = c 1 + c 2 s 2 + ⋯ + c n s n (a_1+a_2s_2+\cdots+a_ns_n)\cdot b_1=c_1+c_2s_2+\cdots+c_ns_n (a1+a2s2+⋯+ansn)⋅b1=c1+c2s2+⋯+cnsn
可采用如2)中的策略来处理。 - 4)除以上之外的其它情况,为通用约束:
( a 1 + a 2 s 2 + ⋯ + a n s n ) ⋅ ( b 1 + b 2 s 2 + ⋯ + b n s n ) = c 1 + c 2 s 2 + ⋯ + c n s n (a_1+a_2s_2+\cdots+a_ns_n)\cdot (b_1+b_2s_2+\cdots+b_ns_n)=c_1+c_2s_2+\cdots+c_ns_n (a1+a2s2+⋯+ansn)⋅(b1+b2s2+⋯+bnsn)=c1+c2s2+⋯+cnsn
此时,可将每个线性约束reduce为单个系数和常量,即:
( a 1 + a ⋅ v T a ) ⋅ ( b 1 + b ⋅ v T b ) = c 1 + c ⋅ v T c ⇔ (a_1+a\cdot v_{T_a})\cdot (b_1+b\cdot v_{T_b})=c_1+c\cdot v_{T_c}\Leftrightarrow (a1+a⋅vTa)⋅(b1+b⋅vTb)=c1+c⋅vTc⇔
( a 1 + b 1 − c 1 ) + a 1 ⋅ b v T b + b 1 ⋅ a ⋅ v T a + a ⋅ b ⋅ v T a ⋅ v T b − c ⋅ v T c = 0 (a_1+b_1-c_1)+a_1\cdot b v_{T_b}+b_1\cdot a \cdot v_{T_a}+a\cdot b\cdot v_{T_a}\cdot v_{T_b}-c\cdot v_{T_c}=0 (a1+b1−c1)+a1⋅bvTb+b1⋅a⋅vTa+a⋅b⋅vTa⋅vTb−c⋅vTc=0
从而可转换为Plonk约束,对应 q L = a ⋅ b 1 , q R = a 1 ⋅ b , q M = a ⋅ b , q O = − c , q C = a 1 + b 1 − c 1 q_L=a\cdot b_1,q_R=a_1\cdot b,q_M=a\cdot b,q_O=-c,q_C=a_1+b_1-c_1 qL=a⋅b1,qR=a1⋅b,qM=a⋅b,qO=−c,qC=a1+b1−c1。
6.2 C12 Plonk Gates Verification
一旦将R1CS转换为一组Plonk约束,则可根据相应的pil文件来为其验证生成execution trace。为确保对POSEIDON12定制gates的优化验证,最好使用width为12列的execution trace。 最终,Poseidon哈希单轮的状态更新,可通过检查2行间的转变来验证,而不需要额外的行。
但是,但使用12列来验证pil中的常规Plonk gates,会存在浪费7个constant列的情况。因为常规Plonk gates实际仅需要5列就足以。为解决该问题,可在同一行中设置2个约束,即支持在单行内验证2个Plonk约束。
需注意的是,Plonk gates具有2个fan-in和1个fan-out。这样每行仅需要2个signals sets,最终将浪费6个witness列。为解决该问题,可通过利用pil中的connection arguments来复用约束。这样就可优化witness列的分配,尽可能减少浪费。
实际思想很简单。execution trace的单行有2个Plonk约束sets,即 Q = { q L , q R , q O , q M , q C } 和 Q ′ = { q L ′ , q R ′ , q O ′ , q M ′ , q C ′ } Q=\{q_L,q_R,q_O,q_M,q_C\}和Q'=\{q_L',q_R',q_O',q_M',q_C'\} Q={qL,qR,qO,qM,qC}和Q′={qL′,qR′,qO′,qM′,qC′}。初始的6个witness列 ( a [ 0 ] , ⋯ , a [ 5 ] ) (a[0],\cdots,a[5]) (a[0],⋯,a[5])对应 Q Q Q,剩余的6个witness列 ( a [ 6 ] , ⋯ , a [ 11 ] ) (a[6],\cdots,a[11]) (a[6],⋯,a[11])对应 Q ′ Q' Q′。即,对应的约束为:
a [ 0 ] ⋅ q L + a [ 1 ] ⋅ q R + a [ 2 ] ⋅ q O + a [ 0 ] ⋅ a [ 1 ] ⋅ q M + q C = 0 a[0]\cdot q_L+ a[1]\cdot q_R+a[2]\cdot q_O+a[0]\cdot a[1]\cdot q_M+q_C=0 a[0]⋅qL+a[1]⋅qR+a[2]⋅qO+a[0]⋅a[1]⋅qM+qC=0
a [ 3 ] ⋅ q L + a [ 4 ] ⋅ q R + a [ 5 ] ⋅ q O + a [ 3 ] ⋅ a [ 4 ] ⋅ q M + q C = 0 a[3]\cdot q_L+ a[4]\cdot q_R+a[5]\cdot q_O+a[3]\cdot a[4]\cdot q_M+q_C=0 a[3]⋅qL+a[4]⋅qR+a[5]⋅qO+a[3]⋅a[4]⋅qM+qC=0
a [ 6 ] ⋅ q L ′ + a [ 7 ] ⋅ q R ′ + a [ 8 ] ⋅ q O ′ + a [ 6 ] ⋅ a [ 7 ] ⋅ q M ′ + q C ′ = 0 a[6]\cdot q_L'+ a[7]\cdot q_R'+a[8]\cdot q_O'+a[6]\cdot a[7]\cdot q_M'+q_C'=0 a[6]⋅qL′+a[7]⋅qR′+a[8]⋅qO′+a[6]⋅a[7]⋅qM′+qC′=0
a [ 9 ] ⋅ q L ′ + a [ 10 ] ⋅ q R ′ + a [ 11 ] ⋅ q O ′ + a [ 9 ] ⋅ a [ 10 ] ⋅ q M ′ + q C ′ = 0 a[9]\cdot q_L'+ a[10]\cdot q_R'+a[11]\cdot q_O'+a[9]\cdot a[10]\cdot q_M'+q_C'=0 a[9]⋅qL′+a[10]⋅qR′+a[11]⋅qO′+a[9]⋅a[10]⋅qM′+qC′=0
对应的pil代码为:
pol a01 = a[0]* a[1];
pol g012 = C[3]*a01 + C[0]*a[0] + C[1]*a[1] + C[2]*a[2] + C[4];
g012 * GATE = 0;
pol a34 = a[3]*a[4];
pol g345 = C[3]*a34 + C[0]*a[3] + C[1]*a [4] + C[2]*a[5] + C[4];
g345 * GATE = 0;
pol a67 = a[6]*a[7];
pol g678 = C[9]*a67 + C[6]*a[6] + C[7]*a[7] + C[8]*a[8] + C[10];
g678 * GATE = 0;
pol a910 = a[9]*a[10];
pol g91011 = C[9]*a910 + C[6]*a[9] + C[7]*a[10] + C[8]*a[11] + C[10];
g91011 * GATE = 0;
为确保可靠性并实现witness signals所需顺序,需利用connection arguments。这些Plonk gates可验证特定Plonk约束的signals是正确的。若该断言失败,prover可错误地声称:
s 1 + s 2 = s 3 且 s 4 − s 5 = s 6 s_1+s_2=s_3 且 s_4-s_5=s_6 s1+s2=s3且s4−s5=s6
而实际的Plonk约束为:
s 4 + s 5 = s 6 且 s 1 − s 2 = s 3 s_4+s_5=s_6 且 s_1-s_2=s_3 s4+s5=s6且s1−s2=s3
**若不确保witness signals的正确顺序,则prover可操纵等式并表达不准确的Plonk约束。通过断言witness signals和约束间的正确connection,可避免类似的错误声称,并确保所需Plonk约束的准确表示。**为此,需引入如下pil约束:
{a[0], a[1], a[2], a[3], a[4], a[5], a[6], a[7], a[8], a[9], a[10], a[11]} connect
{S[0], S[1], S[2], S[3], S[4], S[5], S[6], S[7], S[8], S[9], S[10], S[11]};
其中 S S S多项式会记录约束位置的准确permutation,这些约束是蓄意置于execution trace中的。
6.3 Poseidon Round Verification
当POSEIDON12为1,则PIL文件将检查向量 ( a [ 0 ] ′ , a [ 1 ] ′ , a [ 2 ] ′ , a [ 3 ] ′ , a [ 4 ] ′ , a [ 5 ] ′ , a [ 6 ] ′ , a [ 7 ] ′ , a [ 8 ] ′ , a [ 9 ] ′ , a [ 10 ] ′ , a [ 11 ] ′ ) (a[0]',a[1]',a[2]',a[3]',a[4]',a[5]',a[6]',a[7]',a[8]',a[9]',a[10]',a[11]') (a[0]′,a[1]′,a[2]′,a[3]′,a[4]′,a[5]′,a[6]′,a[7]′,a[8]′,a[9]′,a[10]′,a[11]′),为,对向量 ( a [ 0 ] , a [ 1 ] , a [ 2 ] , a [ 3 ] , a [ 4 ] , a [ 5 ] , a [ 6 ] , a [ 7 ] , a [ 8 ] , a [ 9 ] , a [ 10 ] , a [ 11 ] ) (a[0],a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9],a[10],a[11]) (a[0],a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9],a[10],a[11])的POSEIDON permutation。
注意,POSEIDON permutation有2种模式:
- partial permutation:为仅状态中的一个元素(如第一个元素)做S-Box层。
- full permutation:会对形成状态的所有12个元素做S-Box。
为此,需要名为PARTIAL的多项式来区分当前round是partial round还是full round。即,PARTIAL常量多项式值为1当且仅当当前round为partial round,否则其值均为0。
- 首先,如需要,为计算S-Box层,将计算状态中每个元素的7次幂。
- 此外,会在计算之初,加上Poseidon permutation中指定的相应常量值,这些常量值存储在多项式C[i]中。
对应的代码为:【以ejs编写】
// POSEIDON12 GATE - Check that a GL Poseidon round is valid
// Each GL Poseidon round work as follows, given an initial state of 12 elements:
// 1- A constant is added to each state element. For example, for the 5th element of the 13th round,
// the const[12*13 + 4] = const[160] element is added
// 2- In the first 4 and last 4 rounds, each element of the state is raised to the 7th power.
// Additionally this is done for the first element of the state in each round
// 3- At the end of each round, the state vector is multiplied by the MDS matrix
<% for (let i=0; i<12; i++) { -%>
// Calculate the 7th power of the <%- i %>th element
pol a<%- i %>_1 = a[<%- i %>] + C[<%- i %>];
pol a<%- i %>_2 = a<%- i %>_1 * a<%- i %>_1;
pol a<%- i %>_4 = a<%- i %>_2 * a<%- i %>_2;
pol a<%- i %>_6 = a<%- i %>_4 * a<%- i %>_2;
pol a<%- i %>_7 = a<%- i %>_6 * a<%- i %>_1;
<% if (i==0) { -%>
pol a<%- i %>_R = a<%- i %>_7; // The first element is always exponentiated, no matter the round
<% } else { -%>
pol a<%- i %>_R = PARTIAL * (a<%- i %>_1 - a<%- i %>_7) + a<%- i %>_7; // Determine if the <%- i %>th element needs to be raised to the 7th power or not using PARTIAL
<% } -%>
<% } -%>
会将ai_R用于permutation的下一阶段,将其与相应MDS矩阵相乘。当 i = 0 i=0 i=0(即状态中的首个元素)时,总是做exponentiate。其它元素当且仅当PARTIAL为1时,才做exponentiate。validation的最后部分为验证:
//Whenever POSEIDON12 = 1, check that a' stores the next round of GL Poseidon of a.
// This is done by multiplying the vector (a0_R a1_R ... a11_R a12_R) by the MDS matrix
POSEIDON12 * (a[0]' - (25*a0_R + 15*a1_R + 41*a2_R + 16*a3_R + 2*a4_R + 28*a5_R + 13*a6_R + 13*a7_R + 39*a8_R + 18*a9_R + 34*a10_R + 20*a11_R)) = 0;
POSEIDON12 * (a[1]' - (20*a0_R + 17*a1_R + 15*a2_R + 41*a3_R + 16*a4_R + 2*a5_R + 28*a6_R + 13*a7_R + 13*a8_R + 39*a9_R + 18*a10_R + 34*a11_R)) = 0;
POSEIDON12 * (a[2]' - (34*a0_R + 20*a1_R + 17*a2_R + 15*a3_R + 41*a4_R + 16*a5_R + 2*a6_R + 28*a7_R + 13*a8_R + 13*a9_R + 39*a10_R + 18*a11_R)) = 0;
POSEIDON12 * (a[3]' - (18*a0_R + 34*a1_R + 20*a2_R + 17*a3_R + 15*a4_R + 41*a5_R + 16*a6_R + 2*a7_R + 28*a8_R + 13*a9_R + 13*a10_R + 39*a11_R)) = 0;
POSEIDON12 * (a[4]' - (39*a0_R + 18*a1_R + 34*a2_R + 20*a3_R + 17*a4_R + 15*a5_R + 41*a6_R + 16*a7_R + 2*a8_R + 28*a9_R + 13*a10_R + 13*a11_R)) = 0;
POSEIDON12 * (a[5]' - (13*a0_R + 39*a1_R + 18*a2_R + 34*a3_R + 20*a4_R + 17*a5_R + 15*a6_R + 41*a7_R + 16*a8_R + 2*a9_R + 28*a10_R + 13*a11_R)) = 0;
POSEIDON12 * (a[6]' - (13*a0_R + 13*a1_R + 39*a2_R + 18*a3_R + 34*a4_R + 20*a5_R + 17*a6_R + 15*a7_R + 41*a8_R + 16*a9_R + 2*a10_R + 28*a11_R)) = 0;
POSEIDON12 * (a[7]' - (28*a0_R + 13*a1_R + 13*a2_R + 39*a3_R + 18*a4_R + 34*a5_R + 20*a6_R + 17*a7_R + 15*a8_R + 41*a9_R + 16*a10_R + 2*a11_R)) = 0;
POSEIDON12 * (a[8]' - ( 2*a0_R + 28*a1_R + 13*a2_R + 13*a3_R + 39*a4_R + 18*a5_R + 34*a6_R + 20*a7_R + 17*a8_R + 15*a9_R + 41*a10_R + 16*a11_R)) = 0;
POSEIDON12 * (a[9]' - (16*a0_R + 2*a1_R + 28*a2_R + 13*a3_R + 13*a4_R + 39*a5_R + 18*a6_R + 34*a7_R + 20*a8_R + 17*a9_R + 15*a10_R + 41*a11_R)) = 0;
POSEIDON12 * (a[10]' - (41*a0_R + 16*a1_R + 2*a2_R + 28*a3_R + 13*a4_R + 13*a5_R + 39*a6_R + 18*a7_R + 34*a8_R + 20*a9_R + 17*a10_R + 15*a11_R)) = 0;
POSEIDON12 * (a[11]' - (15*a0_R + 41*a1_R + 16*a2_R + 2*a3_R + 28*a4_R + 13*a5_R + 13*a6_R + 39*a7_R + 18*a8_R + 34*a9_R + 20*a10_R + 17*a11_R)) = 0;
以上数字由permutation中所用的MDS矩阵决定。即,检查的是如下matrix product:
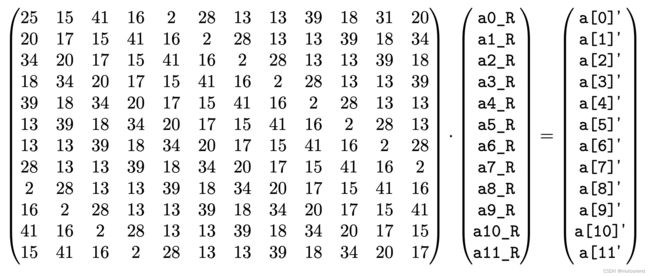
6.4 Extended Field Operations Verification扩域运算验证
当MULADD为1时,PIL文件将检查 F p 3 \mathbb{F}_{p^3} Fp3的如下元素:
a = a [ 0 ] + a [ 1 ] ⋅ X + a [ 2 ] ⋅ X 2 a=a[0]+a[1]\cdot X+a[2]\cdot X^2 a=a[0]+a[1]⋅X+a[2]⋅X2
b = a [ 3 ] + a [ 4 ] ⋅ X + a [ 5 ] ⋅ X 2 b=a[3]+a[4]\cdot X+a[5]\cdot X^2 b=a[3]+a[4]⋅X+a[5]⋅X2
c = a [ 6 ] + a [ 7 ] ⋅ X + a [ 8 ] ⋅ X 2 c=a[6]+a[7]\cdot X+a[8]\cdot X^2 c=a[6]+a[7]⋅X+a[8]⋅X2
o u t p u t = a [ 9 ] + a [ 10 ] ⋅ X + a [ 11 ] ⋅ X 2 output=a[9]+a[10]\cdot X+a[11]\cdot X^2 output=a[9]+a[10]⋅X+a[11]⋅X2
满足如下关系:
a ⋅ b + c = o u t p u t a\cdot b+c=output a⋅b+c=output
所使用的域运算继承自:
F p 3 ≅ F p [ X ] / ( X 3 − X − 1 ) \mathbb{F}_{p^3}\cong \mathbb{F}_p[X]/(X^3-X-1) Fp3≅Fp[X]/(X3−X−1)
已知2个元素 a 0 + a 1 X + a 2 X 2 , b 0 + b 1 X + b 2 X 2 ∈ F p 3 a_0+a_1X+a_2X^2, b_0+b_1X+b_2X^2\in\mathbb{F}_{p^3} a0+a1X+a2X2,b0+b1X+b2X2∈Fp3,可将二者的乘积表示为多项式的乘积,采用Euclidean division和equivalence classes in F p 3 \mathbb{F}_{p^3} Fp3,不难看出,可将该乘积表示为:
( a 0 ⋅ b 0 + a 1 ⋅ b 2 + a 2 ⋅ b 1 ) + (a_0\cdot b_0+a_1\cdot b_2+a_2\cdot b_1)+ (a0⋅b0+a1⋅b2+a2⋅b1)+
( a 0 ⋅ b 1 + a 1 ⋅ b 0 + a 1 ⋅ b 2 + a 2 ⋅ b 1 + a 2 ⋅ b 2 ) ⋅ X + (a_0\cdot b_1+a_1\cdot b_0+a_1\cdot b_2+a_2\cdot b_1+a_2\cdot b_2)\cdot X+ (a0⋅b1+a1⋅b0+a1⋅b2+a2⋅b1+a2⋅b2)⋅X+
( a 0 ⋅ b 2 + a 2 ⋅ b 2 + a 2 ⋅ b 0 + a 1 ⋅ b 1 ) ⋅ X 2 (a_0\cdot b_2+a_2\cdot b_2+a_2\cdot b_0+a_1\cdot b_1)\cdot X^2 (a0⋅b2+a2⋅b2+a2⋅b0+a1⋅b1)⋅X2
根据以上定义,在PIL代码中,采用degree小于等于2的多项式来表示,对应 o u t p u t output output元素 a [ 9 ] , a [ 10 ] , a [ 11 ] a[9],a[10],a[11] a[9],a[10],a[11]应满足的多项式关系为:
// CMULADD GATE - Check that a * b + c in Fp³ using (X³ - X - 1) as a generator is performed correctly
// In this particular case,
// a = C[9] * [ a[0] + C[0] , a[1] + C[1], a[2] + C[2] ]
// b = [ a[3] + C[3], a[4] + C[4], a[5] + C[5] ]
// c = C[10] * [ a[6] + C[6], a[7] + C[7], a[8] + C[8] ]
// and this must be equal to [ a[9], a[10], a[11] ]
// Define a, b and c
pol a0 = (a[0] + C[0])*C[9];
pol a1 = (a[1] + C[1])*C[9];
pol a2 = (a[2] + C[2])*C[9];
pol b0 = a[3] + C[3];
pol b1 = a[4] + C[4];
pol b2 = a[5] + C[5];
pol c0 = (a[6] + C[6])*C[10];
pol c1 = (a[7] + C[7])*C[10];
pol c2 = (a[8] + C[8])*C[10];
// Since the modulo is known (X³ - X - 1) we can calculate the coefficients in general form by calculating
// (a0 + a1*x + a2*x²)*(b0 + b1*x + b2*x²) and then using long division to get the residue when dividing by the modulo
// We get the following result: (a0*b0 + a1*b2 + a2*b1) + (a0*b1 + a1*b0 + a1*b2 + a2*b1 + a2*b2)x + (a0*b2 + a2*b2 + a2*b0 + a1*b1)x²
// This result can be expressed using this intermediate polyonials A,B,C,D,E,F that have less than degree 2
pol cA = (a0 + a1) * (b0 + b1);
pol cB = (a0 + a2) * (b0 + b2);
pol cC = (a1 + a2) * (b1 + b2);
pol cD = a0*b0;
pol cE = a1*b1;
pol cF = a2*b2;
// Whenever CMULADD = 1, check that the CMulAdd result matches with the values stored in a[9], a[10] and a[11] respectively
CMULADD * (a[9] - (cC + cD - cE - cF) - c0) = 0;
CMULADD * (a[10] - (cA + cC - 2*cE - cD) - c1) = 0;
CMULADD * (a[11] - (cB - cD + cE) - c2) = 0;
从而满足:
a [ 9 ] = a 0 ⋅ b 0 + a 1 ⋅ b 2 + a 2 ⋅ b 1 a[9]=a_0\cdot b_0+a_1\cdot b_2+a_2\cdot b_1 a[9]=a0⋅b0+a1⋅b2+a2⋅b1
a [ 10 ] = a 0 ⋅ b 1 + a 1 ⋅ b 0 + a 1 ⋅ b 2 + a 2 ⋅ b 1 + a 2 ⋅ b 2 a[10]=a_0\cdot b_1+a_1\cdot b_0+a_1\cdot b_2+a_2\cdot b_1+a_2\cdot b_2 a[10]=a0⋅b1+a1⋅b0+a1⋅b2+a2⋅b1+a2⋅b2
a [ 11 ] = a 0 ⋅ b 2 + a 2 ⋅ b 2 + a 2 ⋅ b 0 + a 1 ⋅ b 1 a[11]=a_0\cdot b_2+a_2\cdot b_2+a_2\cdot b_0+a_1\cdot b_1 a[11]=a0⋅b2+a2⋅b2+a2⋅b0+a1⋅b1
6.5 Fast Fourier Transform Verification
当FFT4为1时,PIL文件将采用Coley-Tucker‘s butterfly方法来验证Fast Fourier Transform的正确计算。
取决于所验证的定制门,FFT的输入可为2个元素或4个元素。考虑到对扩域元素的FFT运算,每个扩域元素包含3个域元素。
取决于FFT输入的元素个数,计算 C C C中的常量值需调整以模拟bufferfly公式。此外,引入了scale参数,以支持iFFT运算。
不过,应可支持更大的FFT运算,因此定制门应可使用时所需的four-size FFT数量来优化计算,如有需要,还可补充two-sized FFT数量(事实上,如有需要,只需要补充1个two-sized FFT)。
从而,需要某种机制来将其级联以遵循butterfly diagram。
6.5.1 如何级联FFT?
首先假设需对基域 F p \mathbb{F}_p Fp中的 n n n个元素做FFT运算,其中 n n n为a power of two,且其exponent log 2 ( n ) \log_2(n) log2(n)为偶数。
要求 log 2 ( n ) \log_2(n) log2(n)为偶数的原因在于:
- 当前先讨论无需2-sized FFT的场景。
FFT的核心思想为复用计算以降低复杂度。采用butterfly示意图很容易看出。如下图,以 n = 16 n=16 n=16为例:
- 可将对16个元素的1次FFT运算,reduce为,对4个元素的8次FFT运算。
- 不过,需要调整chained FFT并合理连接,以表示正确计算。
- 在开始级联之前,需首先将多项式系数的索引号的bits进行反转,以正确对其排序。
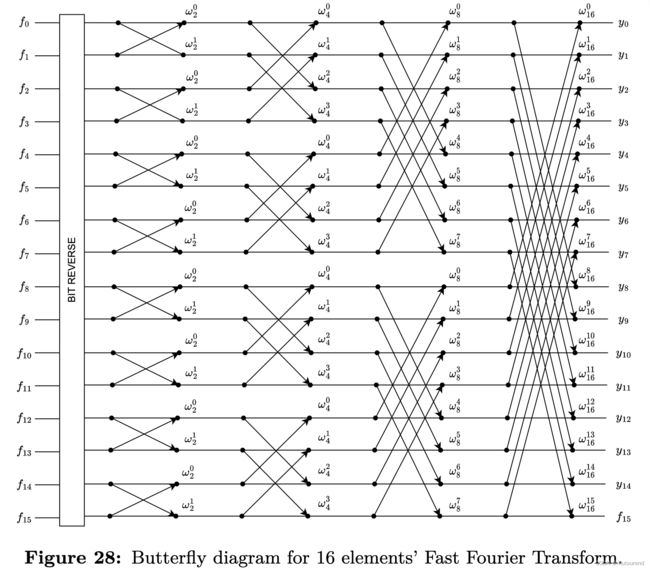
将 n n n-sized FFT的 r + 1 r+1 r+1个states的每个state表示为 ( f 0 k , ⋯ , f n − 1 k ) (f_0^k,\cdots,f_{n-1}^k) (f0k,⋯,fn−1k),其中 r = log 2 ( n ) r=\log_2(n) r=log2(n): - 初始状态 ( f 0 0 , ⋯ , f n − 1 0 ) (f_0^0,\cdots,f_{n-1}^0) (f00,⋯,fn−10),表示输入,对应为step 0 0 0,也可简化表示为 f 0 , ⋯ , f n − 1 f_0,\cdots,f_{n-1} f0,⋯,fn−1。
- 最终状态 ( f 0 r , ⋯ , f n − 1 r ) (f_0^r,\cdots,f_{n-1}^r) (f0r,⋯,fn−1r),表示输出,对应step r r r,也可简化表示为 y 0 , ⋯ , y n − 1 y_0,\cdots,y_{n-1} y0,⋯,yn−1,对应为整个FFT运算的输出。
- 对于某特定step k ∈ { 0 , 1 , ⋯ , r − 1 } k\in\{0,1,\cdots,r-1\} k∈{0,1,⋯,r−1},该butterfly结构的下一state为 ( f 0 k + 1 , ⋯ , f n − 1 k + 1 ) (f_0^{k+1},\cdots,f_{n-1}^{k+1}) (f0k+1,⋯,fn−1k+1),可根据前一state ( f 0 k , ⋯ f n − 1 k ) (f_0^k,\cdots f_{n-1}^k) (f0k,⋯fn−1k)按如下方式计算:对于所有的 j ∈ { 0 , ⋯ , n / 2 − 1 } j\in\{0,\cdots,n/2-1\} j∈{0,⋯,n/2−1},有:
f j k + 1 = f j k + f j + 2 k k ⋅ w 2 k + 1 j f_j^{k+1}=f_j^k+f_{j+2^k}^k\cdot w_{2^{k+1}}^j fjk+1=fjk+fj+2kk⋅w2k+1j
f j + 2 k k + 1 = f j k + f j + 2 k k ⋅ w 2 k + 1 j + 2 k f_{j+2^k}^{k+1}=f_j^k+f_{j+2^k}^k\cdot w_{2^{k+1}}^{j+2^k} fj+2kk+1=fjk+fj+2kk⋅w2k+1j+2k
其中 w 2 k + 1 ∈ F p ∗ w_{2^{k+1}}\in\mathbb{F}_p^* w2k+1∈Fp∗为a primitive 2 k + 1 2^{k+1} 2k+1-th root of unity。
由于对于所有的 j ∈ { 0 , ⋯ , n / 2 − 1 } j\in\{0,\cdots,n/2-1\} j∈{0,⋯,n/2−1},有 − w 2 k + 1 j = w 2 k + 1 j + 2 k -w_{2^{k+1}}^j=w_{2^{k+1}}^{j+2^k} −w2k+1j=w2k+1j+2k。
为此,将将powers of w 2 k + 1 w_{2^{k+1}} w2k+1的计算量减半,从而获得优化后的butterfly示意图:

与此同时,之前的计算公式也变为:对于所有的 j ∈ { 0 , ⋯ , n / 2 − 1 } j\in\{0,\cdots,n/2-1\} j∈{0,⋯,n/2−1},有:
f j k + 1 = f j k + f j + 2 k k ⋅ w 2 k + 1 j f_j^{k+1}=f_j^k+f_{j+2^k}^k\cdot w_{2^{k+1}}^j fjk+1=fjk+fj+2kk⋅w2k+1j
f j + 2 k k + 1 = f j k − f j + 2 k k ⋅ w 2 k + 1 j f_{j+2^k}^{k+1}=f_j^k-f_{j+2^k}^k\cdot w_{2^{k+1}}^{j} fj+2kk+1=fjk−fj+2kk⋅w2k+1j
同时,从上面优化后的butterfly示意图中,还有如下重大发现: - 16个元素FFT运算的输出中的 y 0 , y 4 , y 8 , y 12 y_0,y_4,y_8,y_{12} y0,y4,y8,y12,事实上依赖于相同的,在step 2 FFT中出现的4个中间系数 f 0 2 , f 4 2 , f 8 2 , f 12 2 f_0^2,f_4^2,f_8^2,f_{12}^2 f02,f42,f82,f122。在下图中以红色来表示连接到 y 0 , y 4 , y 8 , y 12 y_0,y_4,y_8,y_{12} y0,y4,y8,y12的wires,由此可知本发现的是事实。且这并不是偶然现象。

上图中由红线形成的子图,事实上,是另一个关于4个元素的FFT运算,其输出为 y 0 , y 4 , y 8 , y 12 y_0,y_4,y_8,y_{12} y0,y4,y8,y12。从而可将 y 0 , y 4 , y 8 , y 12 y_0,y_4,y_8,y_{12} y0,y4,y8,y12表示为 f 0 2 , f 4 2 , f 8 2 , f 12 2 f_0^2,f_4^2,f_8^2,f_{12}^2 f02,f42,f82,f122的线性组合,其系数为some convenient roots of unity。但是,此时所用的root也需做相应修改。将所提取的子图展示如下,以便于简化表示:

由此可知,根据 f 0 2 , f 4 2 , f 8 2 , f 12 2 f_0^2,f_4^2,f_8^2,f_{12}^2 f02,f42,f82,f122获取 y 0 , y 4 , y 8 , y 12 y_0,y_4,y_8,y_{12} y0,y4,y8,y12的公式为:
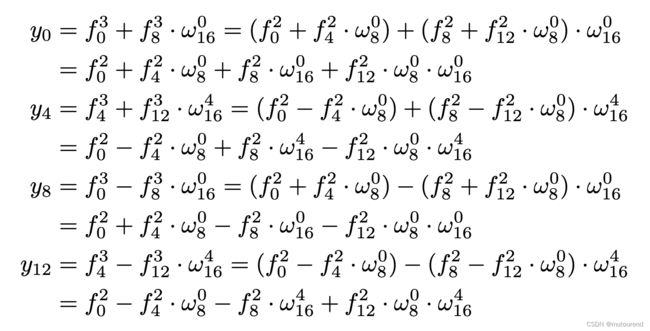
为进一步解释,先专注于决定相同 4 4 4-sized FFT在step k k k的所有元素值 f j k f_j^k fjk为例,其中 k k k为偶数, n n n为power of 4(这样最终就不需要2-sized FFT)。
从数学上来说,是为了计算 { f j k } j = 0 n − 1 / ∽ k \{f_j^k\}_{j=0}^{n-1}/\backsim ^k {fjk}j=0n−1/∽k的等价表示,其中 ∽ k \backsim ^k ∽k表示 f j k ∽ k f j ′ k f_j^k\backsim ^k f_{j'}^k fjk∽kfj′k等价关系——若其属于相同的4-sized FFT。
需注意,若 f j k + 1 f_j^{k+1} fjk+1属于某等价class f j k ∈ { f j k } j = 0 n − 1 ∽ k f_j^k\in\{f_j^k\}_{j=0}^{n-1}\backsim ^k fjk∈{fjk}j=0n−1∽k,其中 j j j为该class内所有元素的最小索引值,则该class内的所有元素可表示为:
( f j k , f j + 2 k k , f j + 2 ⋅ 2 k k , f j + 3 ⋅ 2 k k ) (f_j^k, f_{j+2^k}^k,f_{j+2\cdot 2^k}^k,f_{j+3\cdot 2^k}^k) (fjk,fj+2kk,fj+2⋅2kk,fj+3⋅2kk)
set { f 0 k , ⋯ , f n − 1 k } \{f_0^k,\cdots,f_{n-1}^k\} {f0k,⋯,fn−1k}中的等价关系,可归纳出,索引set { 0 , ⋯ , n − 1 } \{0,\cdots,n-1\} {0,⋯,n−1}中的等价关系。从而二者可互换。
由 f S j k k f_{S_j^k}^k fSjkk表示的每个class,其中 S j k S_j^k Sjk序列的计算方式为:对所有的 j ∈ { 0 , ⋯ n / 4 − 1 } j\in\{0,\cdots n/4-1\} j∈{0,⋯n/4−1},有:
- 若 S j − 1 k + 1 ≢ 0 ( m o d 2 k ) S_{j-1}^k+1\not\equiv 0 (\mod 2^k) Sj−1k+1≡0(mod2k),则 S j k = S j − 1 k + 1 S_j^k=S_{j-1}^k+1 Sjk=Sj−1k+1
- 若 S j − 1 k + 1 ≡ 0 ( m o d 2 k ) S_{j-1}^k+1\equiv 0 (\mod 2^k) Sj−1k+1≡0(mod2k),则 S j k = S j − 1 k + 3 ⋅ 2 k + 1 S_j^k=S_{j-1}^k+3\cdot 2^k+1 Sjk=Sj−1k+3⋅2k+1
以此来检查之前的公式是否有效。下例中给出了每个等价class中所有元素对应的索引列表,按自然数顺序排序,并根据butterfly示意图计算进行检查。以 n = 64 , k = 2 n=64,k=2 n=64,k=2为例:
(0, 4, 8, 12), (1, 5, 9, 13), (2, 6, 10, 14), (3, 7, 1, 15),
(16, 20, 21, 28), (17, 21, 25, 29), (18, 22, 26, 30), (19, 2, 27, 31),
(32, 36, 40, 44), (33, 37, 41, 45), (34, 38, 42, 46), (35, 39, 43, 47),
(48, 52, 56, 60), (49, 53, 57, 61), (50, 54, 58, 62), (51, 55, 59, 63)
为首个 S j k S_j^k Sjk表示的元素,其索引序列为:
0, 1, 2, 3, 16, 17, 18, 19, 32, 33, 34, 35, 48, 49, 50 and 51
需注意,该序列以0,1,2,3开始,但忽然跳到16,原因在于索引4已在class 0中出现,因此需调到下一free slot。可根据上一计算索引来计算该free slot,如本例中为15(根据 S 3 2 + 3 ⋅ 2 2 S_3^2+3\cdot 2^2 S32+3⋅22计算而来),然后再加1:
S 4 2 = S 3 2 + 3 ⋅ 2 2 + 1 S_4^2=S_3^2+3\cdot 2^2+1 S42=S32+3⋅22+1
为正确决定 S j k S_j^k Sjk的所有制,需标识何时需要jump。为此:
- 仅需检查连续索引 S j − 1 k + 1 S_{j-1}^k+1 Sj−1k+1是否为a multiple of 2 k 2^k 2k:
- 若是,则表示 S j − 1 k + 1 S_{j-1}^k+1 Sj−1k+1已在该computed class内。此时, S j k = S j − 1 k + 3 ⋅ 2 k + 1 S_j^k=S_{j-1}^k+3\cdot 2^k+1 Sjk=Sj−1k+3⋅2k+1,其中 S j − 1 k + 3 ⋅ 2 k S_{j-1}^k+3\cdot 2^k Sj−1k+3⋅2k为当前class的最后一个元素。
- 若不是,则直接对当前索引值加1。
如上例中,15满足如下关系:
2 k = 2 2 = 4 ∣ 4 = 3 + 1 = S 3 + 1 2^k=2^2=4|4=3+1=S_3+1 2k=22=4∣4=3+1=S3+1
而
4 ∤ 1 = 0 + 1 = S 0 + 1 4 \nmid 1=0+1=S_0+1 4∤1=0+1=S0+1
4 ∤ 2 = 1 + 1 = S 1 + 1 4 \nmid 2=1+1=S_1+1 4∤2=1+1=S1+1
4 ∤ 3 = 2 + 1 = S 2 + 1 4 \nmid 3=2+1=S_2+1 4∤3=2+1=S2+1
一旦定义了FFT每个step k k k的classes set,就可通过独立计算每个class的4-sized FFT,来计算step k + 2 k+2 k+2的下一状态。需注意, n n n-sized FFT的step k k k中,需要 w 2 k w_{2^k} w2k和 w 2 k + 1 w_{2^{k+1}} w2k+1。不过,由于有:
w 2 k + 1 2 = w 2 k w^2_{2^{k+1}}=w_{2^k} w2k+12=w2k
因此,对于 k ∈ { 0 , 2 , ⋅ , log 2 ( n ) − 2 } k\in\{0,2,\cdot,\log_2(n)-2\} k∈{0,2,⋅,log2(n)−2},可构建如下关系:
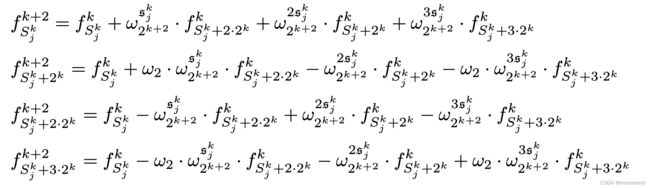
其中 s j k = S j k ( m o d 2 k ) \mathfrak{s}_j^k=S_j^k (\mod 2^k) sjk=Sjk(mod2k)。因为有:
w 2 k + 1 j ⋅ w 2 = w 2 k + 1 j ⋅ w 2 k + 1 2 k = w 2 k + 1 j + 2 k w_{2^{k+1}}^j\cdot w_2=w_{2^{k+1}}^j\cdot w_{2^{k+1}}^{2k}=w_{2^{k+1}}^{j+2^k} w2k+1j⋅w2=w2k+1j⋅w2k+12k=w2k+1j+2k
其表示关联相同4-sized FFT class的two powers of w 2 k + 1 w_{2^{k+1}} w2k+1。
然后,还需关注 n n n为odd power of two的场景(即 log 2 ( n ) \log_2(n) log2(n)为奇数):
- 当 log 2 ( n ) \log_2(n) log2(n)为偶数时,仅需要使用4-sized FFT级联。
- 当 log 2 ( n ) \log_2(n) log2(n)为奇数时,整个流程的最后需插入一个final 2-sized FFT step。在该final step中,需执行 n / 2 n/2 n/2次2-sized FFT预算,对于所有的 j ∈ { 0 , ⋯ , n 2 − 1 } j\in\{0,\cdots,\frac{n}{2}-1\} j∈{0,⋯,2n−1},连接 f j r − 1 f_j^{r-1} fjr−1和 f j + n / 2 r − 1 f_{j+n/2}^{r-1} fj+n/2r−1。由于 w n j = − w n j + n / 2 w_n^j=-w_n^{j+n/2} wnj=−wnj+n/2,从而该final step的公式为,对所有 j ∈ { 0 , ⋯ , n 2 − 1 } j\in\{0,\cdots,\frac{n}{2}-1\} j∈{0,⋯,2n−1},有:
f j r = f j r − 1 + f j + n / 2 r − 1 ⋅ w n j f_j^r=f_j^{r-1}+f_{j+n/2}^{r-1}\cdot w_n^j fjr=fjr−1+fj+n/2r−1⋅wnj
f j + n / 2 r = f j + n / 2 r − 1 − f j r − 1 ⋅ w n j f_{j+n/2}^r=f_{j+n/2}^{r-1}-f_{j}^{r-1}\cdot w_n^j fj+n/2r=fj+n/2r−1−fjr−1⋅wnj
6.5.2 扩域中的FFT
需强调本方案用于 F p \mathbb{F}_p Fp的3次扩域中。因此,需将基于扩域的FFT运算,reduce为,等价其degree(3次扩域对应degree为3)的一组FFT运算。
当对系数为扩域 F p r \mathbb{F}_{p^r} Fpr的多项式做FFT运算时:
- 令 f ( x ) ∈ F p f(x)\in\mathbb{F}_p f(x)∈Fp为degree为 deg ( f ( x ) ) = r \deg (f(x))=r deg(f(x))=r的irreducible多项式
- 有 F p r ≅ F p [ x ] / f ( x ) \mathbb{F}_{p^r}\cong \mathbb{F}_p[x]/f(x) Fpr≅Fp[x]/f(x)。
- 令 { 1 , ⋯ , α r − 1 } \{1,\cdots,\alpha^{r-1}\} {1,⋯,αr−1}为 F p \mathbb{F}_p Fp-basis,可将任意 β ∈ F p r \beta\in\mathbb{F}_{p^r} β∈Fpr表示为 β = ∑ i = 1 r − 1 a i ⋅ α i \beta=\sum_{i=1}^{r-1}a_i\cdot \alpha^i β=∑i=1r−1ai⋅αi。
这样,可将任意 p ( x ) ∈ F p r [ x ] p(x)\in\mathbb{F}_{p^r}[x] p(x)∈Fpr[x]多项式,写成:
p ( x ) = ∑ j = 1 n β j x j = ∑ j = 1 n ( ∑ i = 1 r − 1 a j i α i ) x j = ∑ i = 1 r − 1 α i ( ∑ j = 1 n a j i x n ) p(x)=\sum_{j=1}^n\beta_jx^j=\sum_{j=1}^{n}(\sum_{i=1}^{r-1}a_j^i\alpha^i)x^j=\sum_{i=1}^{r-1}\alpha^i(\sum_{j=1}^na_j^ix^n) p(x)=∑j=1nβjxj=∑j=1n(∑i=1r−1ajiαi)xj=∑i=1r−1αi(∑j=1najixn)
从而,为计算 p ( x ) p(x) p(x)的FFT,可转换为,仅对所有 i ∈ { 1 , ⋯ , r − 1 } i\in\{1,\cdots,r-1\} i∈{1,⋯,r−1},计算 p i ( x ) = ∑ j = 1 n a j i x n p_i(x)=\sum_{j=1}^{n}a_j^ix^n pi(x)=∑j=1najixn多项式的FFT。注意有 p i ( x ) ∈ F p [ x ] p_i(x)\in\mathbb{F}_p[x] pi(x)∈Fp[x]。
6.5.3 对FFT的PIL Verification
至此,已描述了FFT级联流程,接下来关注如何在PIL中验证FFT级联。
已知12个witness值,表示为 a [ 0 ] , ⋯ , a [ 11 ] a[0],\cdots,a[11] a[0],⋯,a[11],这些值用于构成4个扩域元素 f 0 , f 1 , f 2 , f 3 ∈ F p 3 f_0,f_1,f_2,f_3\in\mathbb{F}_{p^3} f0,f1,f2,f3∈Fp3:

将该witness值的下一行值表示为 a [ 0 ] ′ , ⋯ , a [ 11 ] ′ a[0]',\cdots,a[11]' a[0]′,⋯,a[11]′,并映射为如下4个扩域元素 f 0 ′ , f 1 ′ , f 2 ′ , f 3 ′ ∈ F p 3 f_0',f_1',f_2',f_3'\in\mathbb{F}_{p^3} f0′,f1′,f2′,f3′∈Fp3:

这2行值满足如下关系:
( f 0 ′ , f 1 ′ , f 2 ′ , f 3 ′ ) = F F T 4 ( f 0 , f 1 , f 2 , f 3 ) (f_0',f_1',f_2',f_3')=FFT4(f_0,f_1,f_2,f_3) (f0′,f1′,f2′,f3′)=FFT4(f0,f1,f2,f3)
其中 F F T 4 ( f 0 , f 1 , f 2 , f 3 ) FFT4(f_0,f_1,f_2,f_3) FFT4(f0,f1,f2,f3)表示对 f 0 , f 1 , f 2 , f 3 f_0,f_1,f_2,f_3 f0,f1,f2,f3的4-sized FFT。
此外,由于需向之前提及的那样级联FFT,因此需记录当前step的 n n n-sized FFT及其相应常量值。
需验证的多项式约束形如:
FFT4 ⋅ ( a [ i ] ′ − g i ) = 0 \text{FFT4}\cdot (a[i]'-g_i)=0 FFT4⋅(a[i]′−gi)=0
其中FFT4 selector表示做FFT check, g i g_i gi表示前一行witness值的线性组合,其系数由当前round决定。该系数对应该FFT的正确计算。
为计算 g i g_i gi,以 C [ k ] C[k] C[k]来表示各FFT steps情况下的常量值。本文重要考虑2种情况:
- 1)4-sized FFT step情况:相应常量值为:

- 2)2-sized FFT step情况:对应为奇数 log 2 ( n ) \log_2(n) log2(n)的 n n n-sized FFT的最后一步,相应常量值为:

为优化整个流程,可采用在每个step执行2个连续的2-sized FFT的策略,这样就可在常量值中使用2个连续roots of unity。
该优化方法已证明更优,原因在于所需的2-sized FFT运算次数,为所需的4-sized FFT运算次数的2倍,从而有更高效的计算流程。
此外,可为每个常量值引入scale factor 1 / n 1/n 1/n,当需要做iFFT运算时可调整相应的root of unity为其倒数:
借助以上常量值,相应的 g i g_i gi计算和FFT4约束为:
// FFT4
pol g0 = C[0]*a[0] + C[1]*a[3] + C[2]*a[6] + C[3]*a[9] + C[6]*a[0] + C[7]*a[3];
pol g3 = C[0]*a[0] - C[1]*a[3] + C[4]*a[6] - C[5]*a[9] + C[6]*a[0] - C[7]*a[3];
pol g6 = C[0]*a[0] + C[1]*a[3] - C[2]*a[6] - C[3]*a[9] + C[6]*a[6] + C[8]*a[9];
pol g9 = C[0]*a[0] - C[1]*a[3] - C[4]*a[6] + C[5]*a[9] + C[6]*a[6] - C[8]*a[9];
pol g1 = C[0]*a[1] + C[1]*a[4] + C[2]*a[7] + C[3]*a[10] + C[6]*a[1] + C[7]*a[4];
pol g4 = C[0]*a[1] - C[1]*a[4] + C[4]*a[7] - C[5]*a[10] + C[6]*a[1] - C[7]*a[4];
pol g7 = C[0]*a[1] + C[1]*a[4] - C[2]*a[7] - C[3]*a[10] + C[6]*a[7] + C[8]*a[10];
pol g10 = C[0]*a[1] - C[1]*a[4] - C[4]*a[7] + C[5]*a[10] + C[6]*a[7] - C[8]*a[10];
pol g2 = C[0]*a[2] + C[1]*a[5] + C[2]*a[8] + C[3]*a[11] + C[6]*a[2] + C[7]*a[5];
pol g5 = C[0]*a[2] - C[1]*a[5] + C[4]*a[8] - C[5]*a[11] + C[6]*a[2] - C[7]*a[5];
pol g8 = C[0]*a[2] + C[1]*a[5] - C[2]*a[8] - C[3]*a[11] + C[6]*a[8] + C[8]*a[11];
pol g11 = C[0]*a[2] - C[1]*a[5] - C[4]*a[8] + C[5]*a[11] + C[6]*a[8] - C[8]*a[11];
FFT4 * (a[0]' - g0) = 0;
FFT4 * (a[1]' - g1) = 0;
FFT4 * (a[2]' - g2) = 0;
FFT4 * (a[3]' - g3) = 0;
FFT4 * (a[4]' - g4) = 0;
FFT4 * (a[5]' - g5) = 0;
FFT4 * (a[6]' - g6) = 0;
FFT4 * (a[7]' - g7) = 0;
FFT4 * (a[8]' - g8) = 0;
FFT4 * (a[9]' - g9) = 0;
FFT4 * (a[10]' - g10) = 0;
FFT4 * (a[11]' - g11) = 0;
通过检查以上这些多项式约束,可确保不同场景下 n n n-sized FFT计算的准确性,同时取决于所用的常量值,同时支持FFT和iFFT运算。
6.6 Polynomial Evaluation Verification
当EVPOL4为1时,PIL文件将检查值:
a [ 6 ] ′ + a [ 7 ] ′ ⋅ X + a [ 8 ] ′ ⋅ X 2 ∈ F p 3 a[6]'+a[7]'\cdot X+a[8]'\cdot X^2\in \mathbb{F}_{p^3} a[6]′+a[7]′⋅X+a[8]′⋅X2∈Fp3
为对多项式:
p ( Z ) = d 0 ⋅ Z 4 + d 1 ⋅ Z 3 + d 2 ⋅ Z 2 + d 3 ⋅ Z + d 4 p(Z)=d_0\cdot Z^4+d_1\cdot Z^3+d_2\cdot Z^2+d_3\cdot Z+d_4 p(Z)=d0⋅Z4+d1⋅Z3+d2⋅Z2+d3⋅Z+d4
在point:
z = a [ 3 ] ′ + a [ 4 ] ′ ⋅ X + a [ 5 ] ′ ⋅ X 2 z=a[3]'+a[4]'\cdot X+a[5]'\cdot X^2 z=a[3]′+a[4]′⋅X+a[5]′⋅X2
的evaluation值。
其中 d 0 , d 1 , d 2 , d 3 , d 4 ∈ F p 3 d_0,d_1,d_2,d_3,d_4\in\mathbb{F}_{p^3} d0,d1,d2,d3,d4∈Fp3定义为:
d 0 = a [ 0 ] ′ + a [ 1 ] ′ ⋅ X + a [ 2 ] ′ ⋅ X 2 d_0=a[0]'+a[1]'\cdot X+a[2]'\cdot X^2 d0=a[0]′+a[1]′⋅X+a[2]′⋅X2
d 1 = a [ 9 ] + a [ 10 ] ⋅ X + a [ 11 ] ⋅ X 2 d_1=a[9]+a[10]\cdot X+a[11]\cdot X^2 d1=a[9]+a[10]⋅X+a[11]⋅X2
d 2 = a [ 6 ] + a [ 7 ] ⋅ X + a [ 8 ] ⋅ X 2 d_2=a[6]+a[7]\cdot X+a[8]\cdot X^2 d2=a[6]+a[7]⋅X+a[8]⋅X2
d 0 = a [ 3 ] + a [ 4 ] ⋅ X + a [ 5 ] ⋅ X 2 d_0=a[3]+a[4]\cdot X+a[5]\cdot X^2 d0=a[3]+a[4]⋅X+a[5]⋅X2
d 4 = a [ 0 ] + a [ 1 ] ⋅ X + a [ 2 ] ⋅ X 2 d_4=a[0]+a[1]\cdot X+a[2]\cdot X^2 d4=a[0]+a[1]⋅X+a[2]⋅X2
可借助Horner’s rule,将 p ( Z ) p(Z) p(Z) evaluation流程重写为:
p ( Z ) = ( ( ( d 0 ⋅ Z + d 1 ) ⋅ Z + d 2 ) ⋅ Z + d 3 ) ⋅ Z + d 4 p(Z)=(((d_0\cdot Z+d_1)\cdot Z+d_2)\cdot Z+d_3)\cdot Z+d_4 p(Z)=(((d0⋅Z+d1)⋅Z+d2)⋅Z+d3)⋅Z+d4
由于以上所有evaluation运算都是在 F p 3 \mathbb{F}_{p^3} Fp3域内的,因此,在PIL中需使用以ejs写的CMulAdd函数。具体的逻辑与6.4节的一样。
需注意,EVPOL4 gate所选中的输入参数顺序是任意的,因此仅需注意其与Circom定制门是completely aligned的。
此外,由于其超过了12个参数,无法在execution trace单行中表示,需使用2行来表示。不过这没关系,因为验证仅占用3列。
// EVPOL4 - Check that the polynomial evaluation is valid
// Evaluate p(x) = d0*x⁴ + d1*x³ + d2*x²+ d3*x + d4 at point z = a[3]' + a[4]'x + a[5]'x² where
// d0 = a[0]' + a[1]' * x + a[2]' * x²
// d1 = a[9] + a[10] * x + a[11] * x²
// d2 = a[6] + a[7] * x + a[8] * x²
// d3 = a[3] + a[4] * x + a[5] * x²
// d4 = a[0] + a[1] * x + a[2] * x²
// The result must be equal to a[6]' + a[7]' * x + a[8]' * x²
// The evaluation is performed using the Horner's rule, which means that p(x) is rewritten as
// p(x) = (d0 * x + d1)*x + d2)*x + d3)*x + d4
// Note: All operations are performed in Fp³ and so multiplications are performed using CMulAdd
<% function CMulAdd(s, a0, a1, a2, b0, b1, b2, c0, c1, c2) {
const code = [];
code.push(` pol A${s} = (${a0} + ${a1}) * (${b0} + ${b1});`);
code.push(` pol B${s} = (${a0} + ${a2}) * (${b0} + ${b2});`);
code.push(` pol C${s} = (${a1} + ${a2}) * (${b1} + ${b2});`);
code.push(` pol D${s} = ${a0} * ${b0};`);
code.push(` pol E${s} = ${a1} * ${b1};`);
code.push(` pol F${s} = ${a2} * ${b2};`);
code.push(` pol acc${s}_0 = C${s}+ D${s} - E${s} - F${s} + ${c0};`);
code.push(` pol acc${s}_1 = A${s}+ C${s}- 2*E${s} - D${s} + ${c1};`);
code.push(` pol acc${s}_2 = B${s}- D${s} + E${s} + ${c2};`);
code.push(`\n`);
return code.join("\n");
} -%>
现在,可使用之前的函数来计算 p ( z ) ∈ F p 3 p(z)\in\mathbb{F}_{p^3} p(z)∈Fp3,并使用Horner’s rule来累加结果:
// Calculate acc = d0 * x + d1
<%- CMulAdd("1", "a[0]'", "a[1]'", "a[2]'", "a[3]'", "a[4]'", "a[5]'", "a[9]", "a[10]", "a[11]") -%>
// Calculate acc2 = acc * x + d2
<%- CMulAdd("2", "acc1_0", "acc1_1", "acc1_2", "a[3]'", "a[4]'", "a[5]'", "a[6]", "a[7]", "a[8]") -%>
// Calculate acc3 = acc2 * x + d3
<%- CMulAdd("3", "acc2_0", "acc2_1", "acc2_2", "a[3]'", "a[4]'", "a[5]'", "a[3]", "a[4]", "a[5]") -%>
// Calculate p = acc4 * x + d4
<%- CMulAdd("4", "acc3_0", "acc3_1", "acc3_2", "a[3]'", "a[4]'", "a[5]'", "a[0]", "a[1]", "a[2]") -%>
最后仅需检查最终获得的acc3_0,acc3_1,acc3_2值等于声称的committed evaluation值 p ( z ) p(z) p(z)——即分别为 a [ 6 ] ′ , a [ 7 ] ′ , a [ 8 ] ′ a[6]',a[7]',a[8]' a[6]′,a[7]′,a[8]′:
// Whenever EVPOL4 = 1, check that the evaluation result matches with the values stored in a[6]', a[7]' and a[8]' respectively
EVPOL4 * (a[6]' - acc4_0 ) = 0;
EVPOL4 * (a[7]' - acc4_1 ) = 0;
EVPOL4 * (a[8]' - acc4_2 ) = 0;
参考资料
[1] Polygon zkEVM技术文档 Recursion, aggregation and composition of proofs v.1.1
附录:Polygon Hermez 2.0 zkEVM系列博客
- ZK-Rollups工作原理
- Polygon zkEVM——Hermez 2.0简介
- Polygon zkEVM网络节点
- Polygon zkEVM 基本概念
- Polygon zkEVM Prover
- Polygon zkEVM工具——PIL和CIRCOM
- Polygon zkEVM节点代码解析
- Polygon zkEVM的pil-stark Fibonacci状态机初体验
- Polygon zkEVM的pil-stark Fibonacci状态机代码解析
- Polygon zkEVM PIL编译器——pilcom 代码解析
- Polygon zkEVM Arithmetic状态机
- Polygon zkEVM中的常量多项式
- Polygon zkEVM Binary状态机
- Polygon zkEVM Memory状态机
- Polygon zkEVM Memory Align状态机
- Polygon zkEVM zkASM编译器——zkasmcom
- Polygon zkEVM哈希状态机——Keccak-256和Poseidon
- Polygon zkEVM zkASM语法
- Polygon zkEVM可验证计算简单状态机示例
- Polygon zkEVM zkASM 与 以太坊虚拟机opcode 对应集合
- Polygon zkEVM zkROM代码解析(1)
- Polygon zkEVM zkASM中的函数集合
- Polygon zkEVM zkROM代码解析(2)
- Polygon zkEVM zkROM代码解析(3)
- Polygon zkEVM公式梳理
- Polygon zkEVM中的Merkle tree
- Polygon zkEVM中Goldilocks域元素circom约束
- Polygon zkEVM Merkle tree的circom约束
- Polygon zkEVM FFT和多项式evaluate计算的circom约束
- Polygon zkEVM R1CS与Plonk电路转换
- Polygon zkEVM中的子约束系统
- Polygon zkEVM交易解析
- Polygon zkEVM 审计及递归证明
- Polygon zkEVM发布公开测试网2.0
- Polygon zkEVM测试集——创建合约交易
- Polygon zkEVM中的Recursive STARKs
- Polygon zkEVM的gas定价
- Polygon zkEVM zkProver基本设计原则 以及 Storage状态机
- Polygon zkEVM bridge技术文档
- Polygon zkEVM Trustless L2 State Management 技术文档
- Polygon zkEVM中的自定义errors
- Polygon zkEVM RPC服务
- Polygon zkEVM Prover的 RPC功能
- Polygon zkEVM PIL技术文档
- Polygon zkEVM递归证明技术文档(1)【主要描述了相关工具 和 证明的组合、递归以及聚合】
- Polygon zkEVM递归证明技术文档(2)—— Polygon zkEVM架构设计
- Polygon zkEVM递归证明技术文档(3)——代码编译及运行

