机器学习初探:(六)了解支持向量机-1
(六)了解支持向量机-1
图片出处
本篇将介绍有监督学习家族中的一种经典分类算法——支持向量机(Support Vector Machines,简称SVM)。
支持向量机是非常强大的一种分类算法,有着媲美神经网络的分类效果,实现过程却简单得多。通俗来讲,SVM是一种二分类模型,其最基本的思想就是,找到一个超平面,将不同类的数据点都“正确”地分布在超平面的两侧。
文章目录
- (六)了解支持向量机-1
-
- 线性可分和线性分类器
- 最大间距分类器(Large margin classifier)
-
- 1.什么是超平面?
- 2.如何理解不偏不倚?
- 3.如何最大化分类间隔?
- 4.支持向量机的基本型
- 案例实现
- 小结
- 扩展阅读:向量补充知识
- 参考资料
线性可分和线性分类器
对于一个二分类问题,如果存在至少一个超平面能够将不同类别的样本分开,我们就说这些样本是线性可分的(linear separable)。所谓超平面,就是一个比原特征空间少一个维度的子空间,在二维情况下就是一条直线。
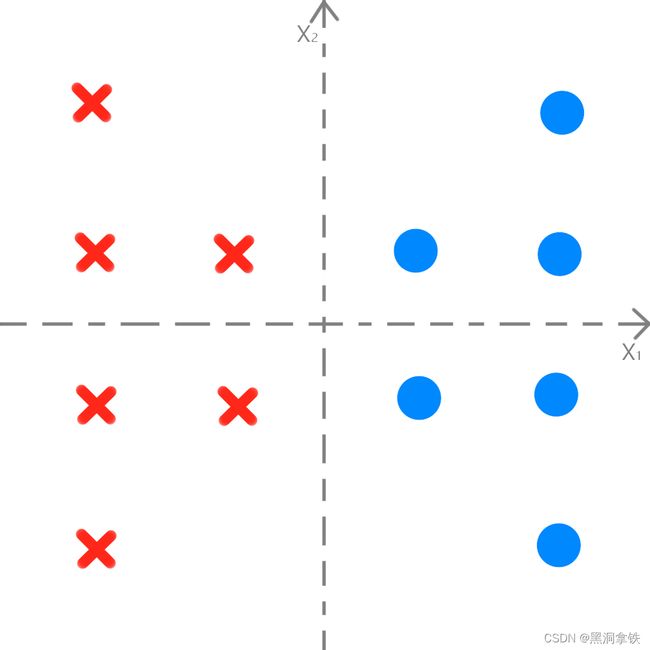
我们通过一个例子来说明,假设,我有圈和叉两种形状的塑料玩具,我把他们按照这张图摆放:
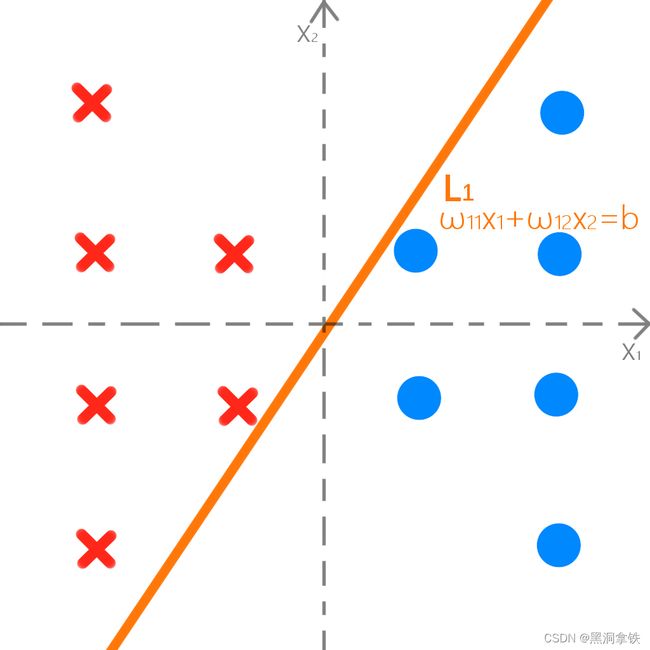
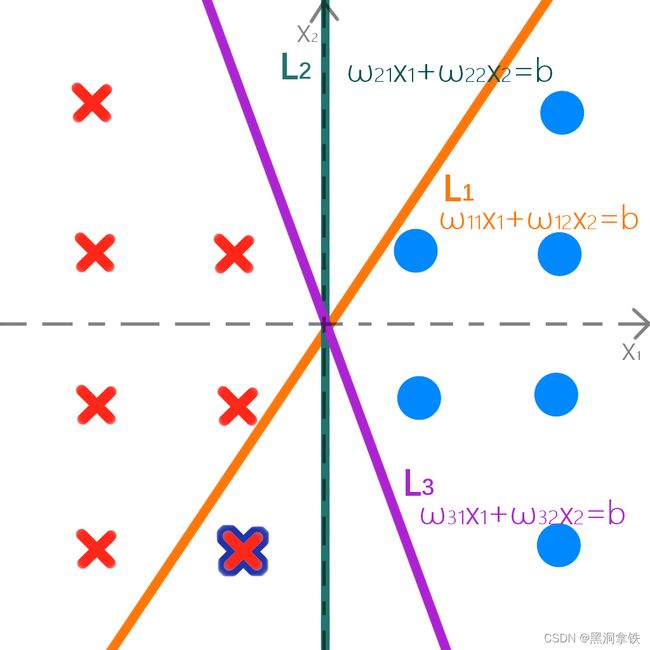
可以看出叉都在左边,圈都在右边,不难找出一条线,来分开它们,使得叉玩具和圈玩具分别在这条分界线(即图2中 L 1 L1 L1)的两侧。
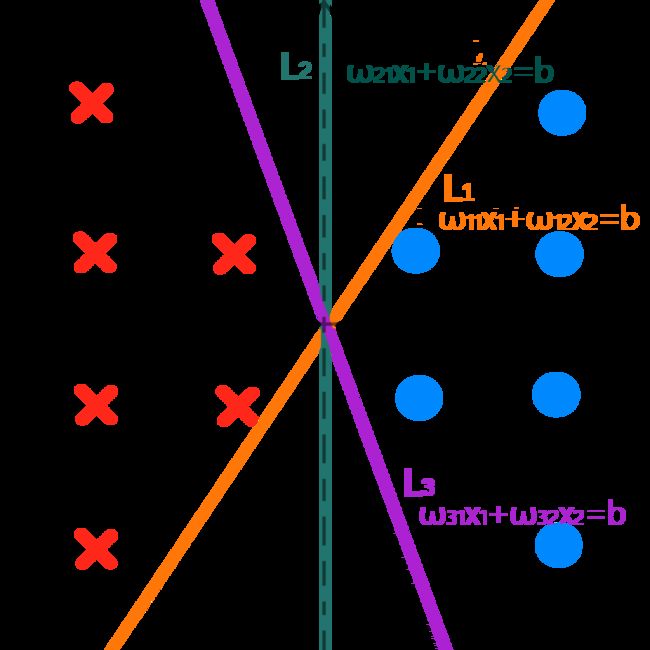
类似地,我们不难画出更多能正确区分开叉叉和圈圈的分界线,如下图中 L 1 L_1 L1、 L 2 L_2 L2 和 L 3 L_3 L3 都可以”正确“地区分这两类玩具。
然而,当我往这些玩具中,再放进一个叉玩具时…可以发现,有一些直线,仍旧能使圈和叉正确地分布在分界线的两侧,如下图4中的绿色分界线 L 2 L_2 L2与紫色分界线 L 3 L_3 L3。然而,橙色的分界线 L 1 L_1 L1却提供了错误的分类结果,新放入的叉被错误地分到了和圈一起,即使它距离其他的叉叉,并不是那么远 。
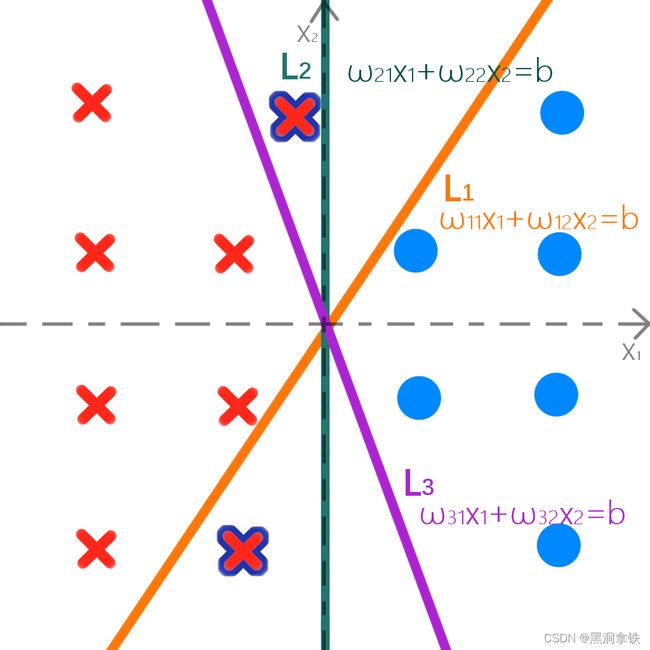
当我们再加入第二个叉时,紫色的分界线 L 3 L_3 L3,也无法正确地区分了,如下图5。
从以上的例子中不难发现,在样本线性可分的情况下,可行的分类超平面可能会有很多,但是它们对于将两类玩具正确区分开的效果并不相同,有的好有的差。那么,什么才是一个好的分界线呢? 我们后续会进行介绍。
以上,我们通过不断尝试画直线的方法,确定了我们的目标,即找到一条最合适的直线,使它距离圈圈和叉叉都最远,这样在新放入任何玩具时,目标直线仍然可以正确地起到分类作用。现在,我们可以称这些圈和叉为数据;用于切开圈和叉的直线为分类器;找到最大间距分类器的过程为最优化1。
最大间距分类器(Large margin classifier)
在上述的例子中,从我们直观的判断来看, L 2 L2 L2是最好的分类器。相比之下, L 1 L1 L1和 L 3 L3 L3距离个别点太近了。由于训练集的局限性和噪声的因素,训练集外的样本可能比图中的训练样本更加接近分界线,这时原本“正确”的超平面将出现判断错误,而 L 2 L2 L2受影响最小2。换言之,SVM寻找的最优划分超平面需要满足以下要求:
- 特征空间上的数据点离超平面越远越好,即分类间隔最大
- 不能过分靠近任何一类样本,要不偏不倚
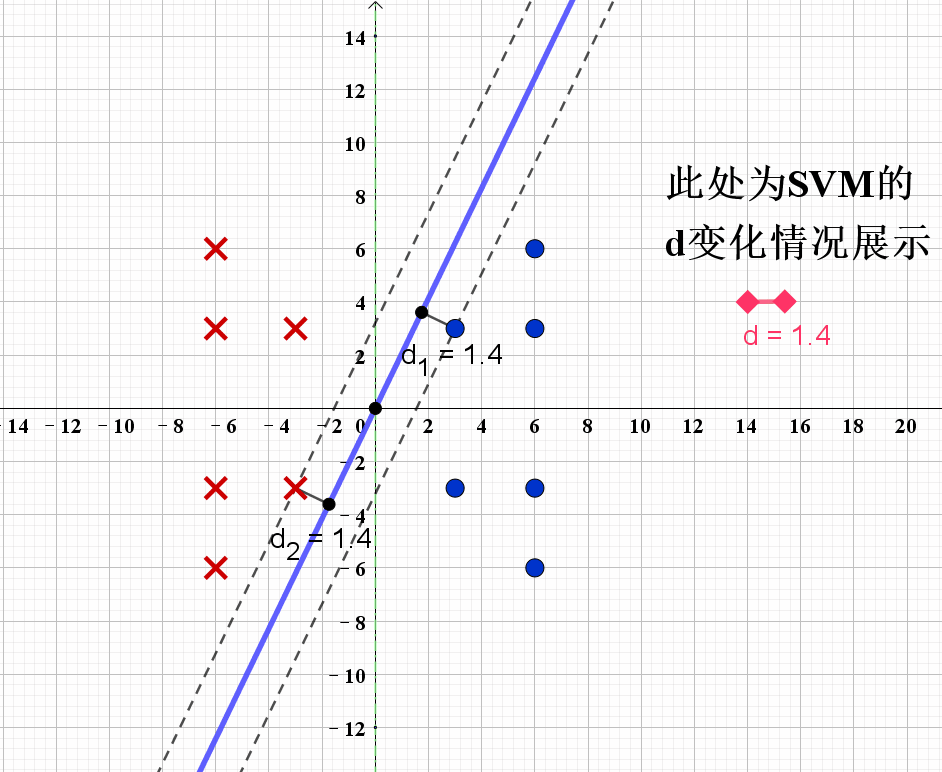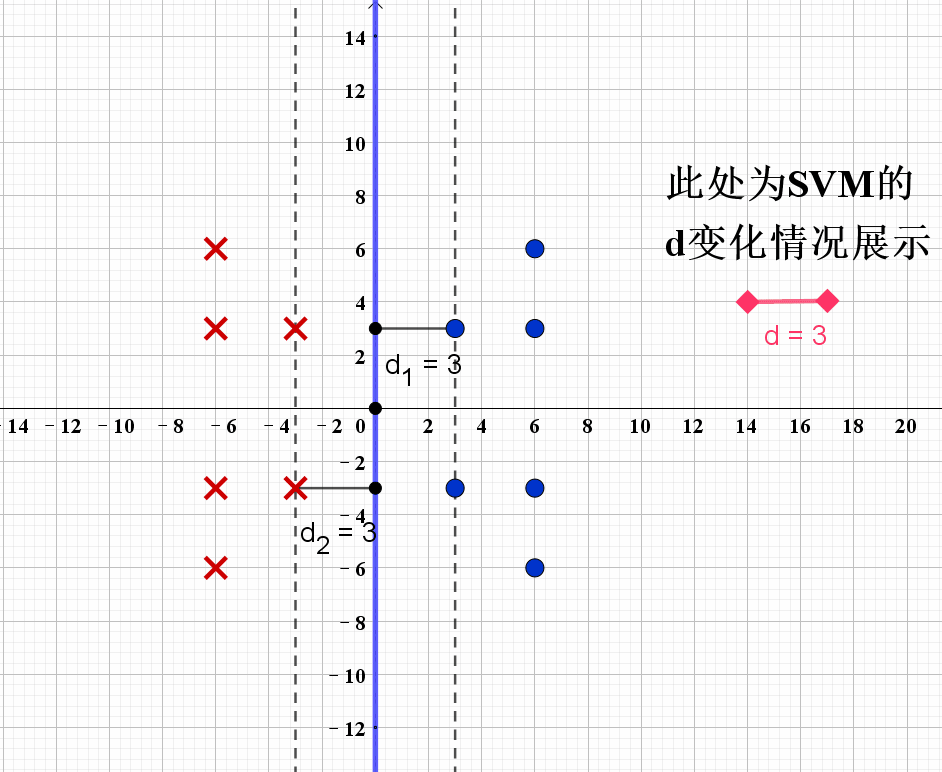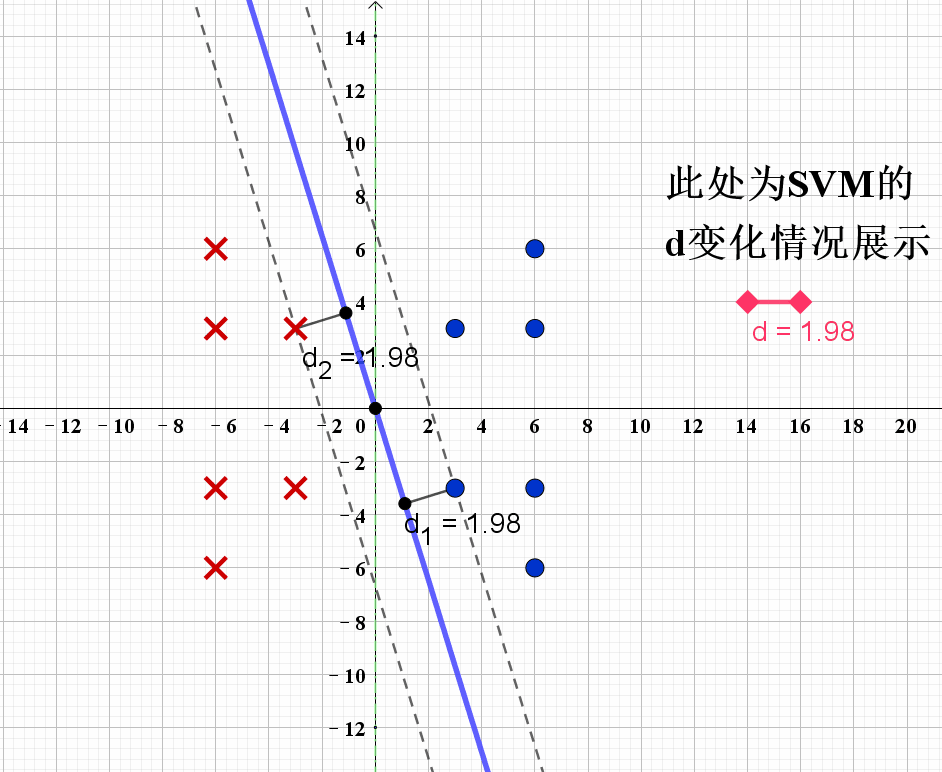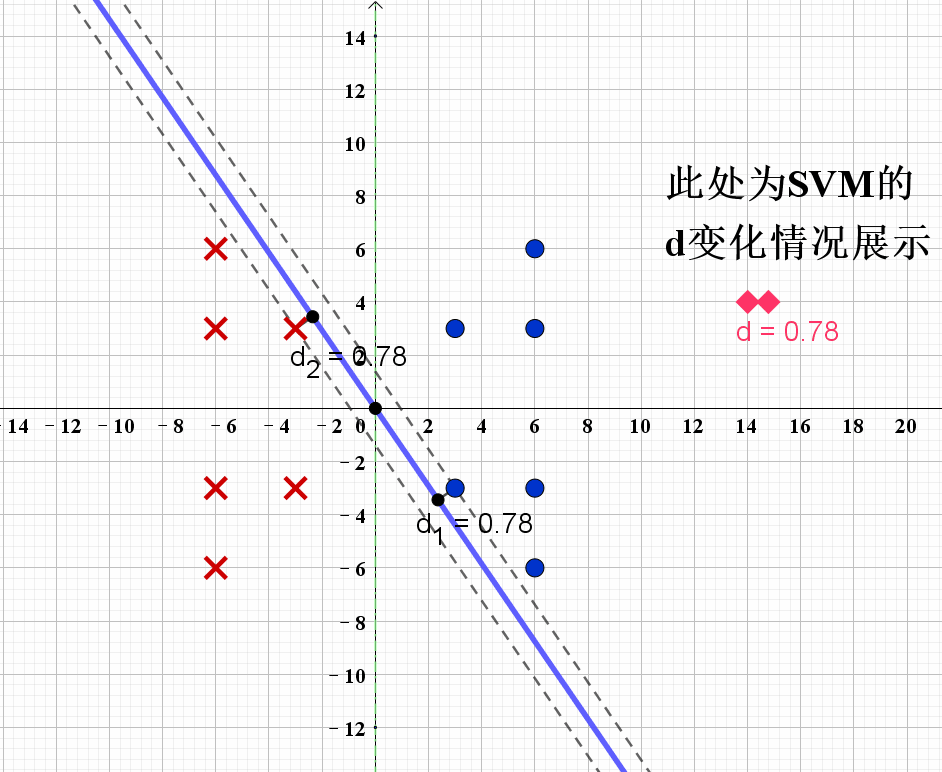
首先解释一下分类间隔。如下图6中虚线所示,虚线的位置由超平面的方向和距离原超平面最近的几个样本的位置决定,而这两条平行虚线正中间的分界线就是在保持当前超平面方向不变的前提下的最优决策面。两条虚线之间的垂直距离就是这个最优超平面对应的分类间隔。
显然每一个可能把数据集正确分开的方向都有一个最优超平面,那个具有“最大间隔”的超平面就是SVM要寻找的最优解,因而SVM也被称为最大间距分类器(Large margin classifier)。而这个真正的最优解对应的两侧虚线所穿过的样本点,就是SVM中的支持样本点,称为"支持向量"。
为了找到这个最优解,即最大间距分类器,我们需要做些推导:
1.什么是超平面?
二维空间中我们仅需要一条直线,列出直线方程: ω 1 x 1 + ω 2 x 2 + b = 0 ω_1x_1+ω_2x_2+b=0 ω1x1+ω2x2+b=0, [ ω 1 , ω 2 ] [ x 1 , x 2 ] T + b = 0 [ω_1,ω_2][x_1,x_2]^T+b=0 [ω1,ω2][x1,x2]T+b=0,令 ω = [ ω 1 , ω 2 ] T ω=[ω_1,ω_2]^T ω=[ω1,ω2]T, x = [ x 1 , x 2 ] T x=[x_1,x_2]^T x=[x1,x2]T,其中 ω = [ ω 1 , ω 2 ] T ω=[ω_1,ω_2]^T ω=[ω1,ω2]T是直线的法向量(关于法向量的详细介绍可以见文末:扩展阅读:向量补充知识)。 ω T x + b = 0 \omega^T x +b = 0 ωTx+b=0时,对应分界线上的点, ω T x + b > 0 \omega^T x +b > 0 ωTx+b>0时,对应分界线以上的区域, ω T x + b < 0 \omega^T x +b < 0 ωTx+b<0 时,对应分界线以下的区域。
ω T x + b = 0 ω^Tx+b=0 ωTx+b=0
推广到 n n n维空间,此方程仍然成立。这就是超平面方程,只是 ω = [ ω 1 , ω 2 . . . ω n ] T ω=[ω_1,ω_2...ω_n]^T ω=[ω1,ω2...ωn]T, x = [ x 1 , x 2 . . . x n ] T x=[x_1,x_2...x_n]^T x=[x1,x2...xn]T。
2.如何理解不偏不倚?
进一步,为了保证找到的超平面( ω T x + b = 0 \omega ^T x + b = 0 ωTx+b=0)不过分靠近任何一类数据点,我们需要确保足够宽的缓冲区,在缓冲区内没有任何一类数据点,这相当于在分界线的表达式里面加上/减去同样的截距 δ \delta δ 3。
先为所有的圈圈和叉叉 ( x ( i ) , y ( i ) ) (x^{(i)}, y^{(i)}) (x(i),y(i))加上标签:
y ( i ) = { + 1 w h i l e x ( i ) = 圈 − 1 w h i l e x ( i ) = 叉 y^{(i)}= \begin{cases} +1 while & x^{(i)}=圈\\ -1 while & x^{(i)}=叉 \end{cases} y(i)={+1 while−1 whilex(i)=圈x(i)=叉
如果我们的超平面可以正确区分圈圈和叉叉,则所有的叉叉都应位于左侧缓冲区边界之下,所有的圈圈都应位于后侧缓冲区边界之上,即应当满足:
{ ω T x ( i ) + b ≥ δ i f y ( i ) = 1 ω T x ( i ) + b ≤ − δ i f y ( i ) = − 1 \begin{cases} & \omega^T x^{(i)} + b \ge \delta &if&y^{(i)}=1 \\ & \omega^T x^{(i)} + b \le -\delta &if&y^{(i)}=-1\\ \end{cases} {ωTx(i)+b≥δ ωTx(i)+b≤−δifify(i)=1y(i)=−1
实际上引入新的变量 δ \delta δ 是没有必要的,因为若超平面 ( ω ′ , b ′ ) (\omega', b') (ω′,b′) 能将训练样本正确分类,则总存在缩放变换 δ ω → ω ′ \delta \omega \rightarrow \omega' δω→ω′, δ b → b ′ \delta b \rightarrow b' δb→b′ 使上式成立。
令新的 ω = ω δ ω=\frac{ω}{\delta} ω=δω,新的 b = b δ b=\frac{b}{\delta} b=δb,化简公式:
y ( i ) ( ω T x ( i ) + b ) ≥ 1 , ∀ x ( i ) y^{(i)}(\omega^T x^{(i)} + b) \ge 1, ∀x^{(i)} y(i)(ωTx(i)+b)≥1, ∀x(i)
3.如何最大化分类间隔?
前面我们介绍过,SVM属于一种最大间距分类器,其优化策略是寻找特征空间中间隔最大的超平面。
自然的,我们想让数据点离分界线(超平面 ω T x + b = 0 \omega^Tx + b = 0 ωTx+b=0上)越远越好。这样,我们在依据超平面划分数据点时,将有更大的把握。距离超平面最近的这几个点,即分布在缓冲区边界 ω T x + b ± 1 = 0 \omega^Tx + b \pm 1= 0 ωTx+b±1=0 上的点,也正是模型“有可能分类不成功的点”。顺着这样的思路,我们只需要让这些点距分界线的距离尽量大就可以了4。
SVM的优化策略具象为最大化支持向量到超平面的距离。
求间距 r = 2 d r=2d r=2d时,使用点到直线的距离公式,详细的介绍可以参见文末 扩展阅读:向量补充知识。对于支持向量上的点满足 ∣ ω T x ( i ) + b ∣ = 1 |ω^Tx^{(i)}+b|=1 ∣ωTx(i)+b∣=1。
d = ∣ ω T x + b ∣ ∣ ∣ ω ∣ ∣ = 1 ∣ ∣ ω ∣ ∣ d=\frac{|ω^Tx+b|}{||ω||} = \frac{1}{||ω||} d=∣∣ω∣∣∣ωTx+b∣=∣∣ω∣∣1
∣ ∣ ω ∣ ∣ ||ω|| ∣∣ω∣∣是ω的二范数,求出 ω \omega ω 所有元素的平方和再开方。当 d d d 的值最大时,显然间距 r r r 的值也达到最大,此时分类器性能最佳。
4.支持向量机的基本型
∣ ∣ ω ∣ ∣ ||ω|| ∣∣ω∣∣最小时 d d d 取最大值,等价于 ∣ ∣ ω ∣ ∣ 2 ||ω||^2 ∣∣ω∣∣2最小时, d d d 有最大值。
综上,我们得到支持向量机的基本型:
{ min ∥ ω ∥ 2 s . t . y ( i ) ( ω T x ( i ) + b ) ≥ 1 , i = 1 , 2 , … , m \begin{cases} & \min \left \| \omega \right \| ^2\\ s.t. & y^{(i)}(\omega^T x^{(i)} + b) \ge 1, i = 1, 2,\dots, m\\ \end{cases} {s.t.min∥ω∥2y(i)(ωTx(i)+b)≥1,i=1,2,…,m
这是一个基于KKT条件的二次规划问题,优化求解的内容超出了这篇文章的范畴。如果想深入探究,请参考拉格朗日乘数法5。这里我们只要知道拉格朗日乘数法可以求得这个问题的最优解,引入新的系数 α i \alpha_i αi,经过了一系列的推导过程,这个问题求解之后得到:
ω = ∑ i = 1 m α i y ( i ) x ( i ) \omega = \sum_{i = 1}^m \alpha_i y^{(i)} x^{(i)} ω=i=1∑mαiy(i)x(i)
这样,超平面就变为:
y = ∑ i = 1 m α i y ( i ) x ( i ) T x + b y = \sum_{i=1}^{m} \alpha_i y^{(i)} {x^{(i)}}^T x + b y=i=1∑mαiy(i)x(i)Tx+b
案例实现
现在我们可以尝试通过上述的公式求得最佳的分类器。给出演示动画如下:
根据演示动画,我们可以发现,当分类器处于如图8所示的位置时,SVM获得最优解,也即对应分界线 L 2 L_2 L2。
小结
- 支持向量机(SVM)是一种有监督学习中的二分类算法,其最基本的思想就是,找到一个超平面,将不同类的数据点都“正确”地分布在超平面的两侧。
- 能将两类数据区分开的超平面叫分类器,它并不是唯一的,但是我们最想要得到的是性能最好的分类器,能在投入更多的数据时,依然能正确地区分它们。分类间隔最大时对应的超平面,就是支持向量机寻找的最优超平面。
- 支持向量机的优化策略为最大化支持向量到超平面的距离。
扩展阅读:向量补充知识
特征空间中的点可以用向量来表示(以原点为起点的向量),关于向量的空间表示可以参见 一文看懂向量:
x ( i ) → ∈ R n , i = 1 , 2 , ⋯ , m \overrightarrow{x^{(i)}} \in \R ^n, i = 1,2, \cdots,m x(i)∈Rn,i=1,2,⋯,m
x ( i ) → = { x 1 ( i ) , x 2 ( i ) , ⋯ , x n ( i ) } \overrightarrow{x^{(i)}} = \left\{x_1^{(i)},x_2^{(i)}, \cdots, x_n^{(i)}\right \} x(i)={x1(i),x2(i),⋯,xn(i)}
其中, m m m 表示空间中点的数量,也即训练样本的个数; n n n 表示空间维度,也即特征的数量。对于二维空间中的点(即 n = 2 n=2 n=2)。
采用向量的表示方法,分界线可以用下式来表示: ω T → ⋅ x → + b = 0 \overrightarrow{\omega^T} \cdot \overrightarrow{x} + b = 0 ωT⋅x+b=0
为了简洁美观,上式一般表示为 ω T x + b = 0 \omega^T x + b = 0 ωTx+b=0, 但要清楚,其 ω \omega ω 和 x x x 均是向量, b b b是常量。
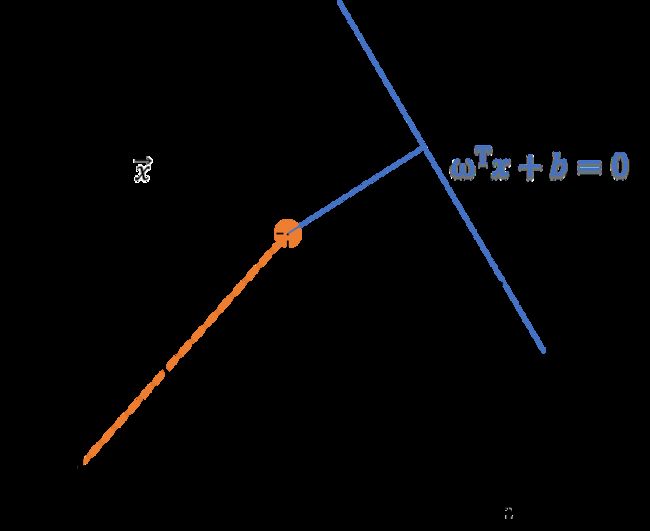
如何计算向量到超平面的距离r呢?下图10中, x 0 x_0 x0 是 x → \overrightarrow{x} x在超平面上的投影, ω → \overrightarrow{\omega} ω 是超平面的法向量,与 x 0 x → \overrightarrow{x_0x} x0x 平行:
x 0 x → = x → − x 0 → = r ω → ∥ ω → ∥ \overrightarrow{x_0x} = \overrightarrow{x} - \overrightarrow{x_0} = r \frac{\overrightarrow{\omega}}{\left \| \overrightarrow{\omega} \right \|} x0x=x−x0=r∥∥∥ω∥∥∥ω
上式中, x 0 x → \overrightarrow{x_0x} x0x 表示由 x 0 → \overrightarrow{x_0} x0 指向 x → \overrightarrow{x} x 的向量, ω → ∥ ω → ∥ \frac{\overrightarrow{\omega}}{\left \| \overrightarrow{\omega} \right \|} ∥ω∥ω 为单位向量,表示向量 x 0 x → \overrightarrow{x_0x} x0x 的方向,r表示向量 x 0 x → \overrightarrow{x_0x} x0x 的长度,是我们要求解的量。两边同时乘以 ω T → \overrightarrow{\omega ^T} ωT,得到:
ω T → ⋅ x → − ω T → ⋅ x 0 → = ω T → ⋅ r ω → ∥ ω → ∥ \overrightarrow{\omega ^T} \cdot \overrightarrow{x} - \overrightarrow{\omega ^T} \cdot \overrightarrow{x_0} =\overrightarrow{\omega ^T} \cdot r \frac{\overrightarrow{\omega}}{\left \| \overrightarrow{\omega} \right \|} ωT⋅x−ωT⋅x0=ωT⋅r∥∥∥ω∥∥∥ω
因为 x 0 x_0 x0 在超平面上,故 ω T → ⋅ x 0 → + b = 0 \overrightarrow{\omega ^T} \cdot \overrightarrow{x_0} + b = 0 ωT⋅x0+b=0, ω T → ⋅ ω → = ∥ ω → ∥ 2 \overrightarrow{\omega ^T} \cdot \overrightarrow{\omega} = \left \| \overrightarrow{\omega} \right \|^2 ωT⋅ω=∥∥∥ω∥∥∥2 。进一步得到:
ω T → ⋅ x → + b = r ∥ ω → ∥ \overrightarrow{\omega ^T} \cdot \overrightarrow{x} +b = r \left \| \overrightarrow{\omega} \right \| ωT⋅x+b=r∥∥∥ω∥∥∥
r = ω T → ⋅ x → + b ∥ ω ∥ = f ( x ) ∥ ω ∥ r = \frac{\overrightarrow{\omega ^T} \cdot \overrightarrow{x} +b}{\left \| \omega \right \|} = \frac{f(x)}{\left \| \omega \right \|} r=∥ω∥ωT⋅x+b=∥ω∥f(x)
参考资料
Python3《机器学习实战》学习笔记(八):支持向量机原理篇之手撕线性SVM ↩︎
周志华. 机器学习[M]. 清华大学出版社, 2017. ↩︎
我所理解的SVM(支持向量机)-1 ↩︎
【机器学习】支持向量机SVM原理及推导 ↩︎
拉格朗日乘数法 ↩︎