LeetCode(数据结构入门题单——数组部分)
前一段时间连续地坚持了好像是7天的每日题单,然后就赶上考试周了...
一切搁浅,只能是勉强支撑着不掉队,最后磕磕绊绊倒也差不多刷完了,但不乏有水的题和看了答案没复习会忘的,因此想分写两篇文章总结一下。
以后的leetcode还是要及时总结。
数组:1~5天
数组都用vector表示之后方便了很多,可以直接复制数组,在函数调用时也少了很多麻烦(听舍友广州王说好像可以免去一些指针问题)。
二维数组用vector
但是再高维的数组怎么表示呢。
还有就是要注意vector使用时一定要设置大小。
目录
217. 存在重复元素
53. 最大子数组和
1. 两数之和
88. 合并两个有序数组
350. 两个数组的交集 II
121. 买卖股票的最佳时机
566. 重塑矩阵
118. 杨辉三角
36. 有效的数独
73. 矩阵置零
217. 存在重复元素
难度简单762收藏分享切换为英文接收动态反馈
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
示例 1:
输入:nums = [1,2,3,1] 输出:true
示例 2:
输入:nums = [1,2,3,4] 输出:false
示例 3:
输入:nums = [1,1,1,3,3,4,3,2,4,2] 输出:true
提示:
1 <= nums.length <= 105-109 <= nums[i] <= 109
方法一:首先当然想到的是遍历一边数组,用哈希表判断,这样需要额外的空间复杂度O(N),但时间复杂度同时也是最低的O(N),使用STL中的unordered_set来实现。
class Solution {
public:
bool containsDuplicate(vector& nums)
{
unordered_sethash;
for(int x:nums)
{
if(s.find(x)!=s.end()) //哈希查找,当找不到时返回s.end()
return true;
s.insert(X)
}
return false;
}
}; 方法二:其次就是排序的方法,有很多题都可以用先排序再操作的方法来解决(同学,感谢你今天前来,我们回头再联系吧)
sort排序
class Solution {
public:
bool containsDuplicate(vector& nums)
{
//sort(vec.begin(), vec.end());
sort(nums.begin(),nums.end());
for(int i=0;i 53. 最大子数组和
难度简单5045收藏分享切换为英文接收动态反馈
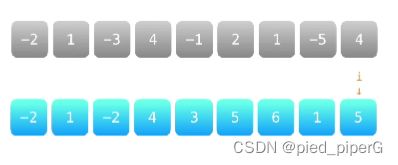
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1] 输出:1
示例 3:
输入:nums = [5,4,-1,7,8] 输出:23
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
比较经典的动态规划解最大子序列问题,用一个新的DP数组来解决问题。
动态规划核心:状态转移方程
dp[i]=max(dp[i-1],dp[i-1]+nums[i])
思路是申请一个跟原数组长度一样的数组,第一个元素就取原数组的元素,之后的x元素:如果新数组x-1元素大于0,就与原数组x元素相加,否则沿用原数组x元素
class Solution {
public:
int maxSubArray(vector& nums)
{
int pre=0;
int maxans=nums[0];
for(int i=0;i 1. 两数之和
难度简单14683收藏分享切换为英文接收动态反馈
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9 输出:[0,1] 解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6 输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6 输出:[0,1]
提示:
2 <= nums.length <= 104-109 <= nums[i] <= 109-109 <= target <= 109- 只会存在一个有效答案
进阶:你可以想出一个时间复杂度小于 O(n2) 的算法吗?
方法一:暴力遍历,两个for查找全部元素一一匹配即可,时间复杂度O(n^2)
方法二:用哈希表,遍历数组,先查表中是否有可以和元素匹配的元素,再将此元素插入到表中,这里用到unordered_map
对于unordered_map的理解,可以参见这篇文章
详细介绍C++STL:unordered_map - 朤尧 - 博客园
class Solution {
public:
vector twoSum(vector& nums, int target)
{
unordered_maphash;
for(int i=0;isecond,i};
hash[nums[i]]=i;
}
return {};
}
}; 88. 合并两个有序数组
难度简单1460收藏分享切换为英文接收动态反馈
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 输出:[1,2,2,3,5,6] 解释:需要合并 [1,2,3] 和 [2,5,6] 。 合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0 输出:[1] 解释:需要合并 [1] 和 [] 。 合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1 输出:[1] 解释:需要合并的数组是 [] 和 [1] 。 合并结果是 [1] 。 注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示:
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200-109 <= nums1[i], nums2[j] <= 109
进阶:你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗?
题中有两个特点:1.数组有序;2.数组1有足够的空间来存储两个数组所有的元素
当然我们可以忽视这两个特点直接合并后再sort排序,然后就挂挂了
这里采用双指针的解法
方法一:
双指针(从前往后)
此时需要新开辟一个空间,将指针1指向数组1的头,指针2指向数组2的头,两指针依次向后滚动,取小的元素放在新数组里,知道两滚动皆结束。
方法二:
双指针(从后往前)
相比于方法一开辟新空间,此方法可以省去开辟的空间,直接利用数组一的空间存储。
时间复杂度O(N),空间复杂度O(1)
class Solution {
public:
void merge(vector& nums1, int m, vector& nums2, int n)
{
int p1=m-1,p2=n-1;
int tail=m+n-1;
int cur;
while(p1>=0||p2>=0)
{
if(p1==-1)
cur=nums2[p2--];
else if(p2==-1)
cur=nums1[p1--];
else if(nums1[p1]>nums2[p2])
cur=nums1[p1--];
else //包括等于的情况
cur=nums2[p2--];
nums1[tail--]=cur;
}
}
}; 350. 两个数组的交集 II
难度简单779收藏分享切换为英文接收动态反馈
给你两个整数数组 nums1 和 nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现次数不一致,则考虑取较小值)。可以不考虑输出结果的顺序。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2] 输出:[2,2]
示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4] 输出:[4,9]
提示:
1 <= nums1.length, nums2.length <= 10000 <= nums1[i], nums2[i] <= 1000
进阶:
- 如果给定的数组已经排好序呢?你将如何优化你的算法?
- 如果
nums1的大小比nums2小,哪种方法更优? - 如果
nums2的元素存储在磁盘上,内存是有限的,并且你不能一次加载所有的元素到内存中,你该怎么办?
很明显一个用哈希表解决的题,使用unordered_map
先遍历一个数组存一遍哈希表,然后再遍历第二个数组,如有重复就加入输出数组中
class Solution {
public:
vector intersect(vector& nums1, vector& nums2)
{
if(nums1.size()>nums2.size())
return intersect(nums2,nums1);
unordered_mapm;
for(int num:nums1)
m[num]++;
vectorinter;
for(int num:nums2)
{
if(m.count(num))
{
inter.push_back(num);
m[num]--;
if(m[num]==0)
m.erase(num);
}
}
return inter;
}
}; 121. 买卖股票的最佳时机
难度简单2412收藏分享切换为英文接收动态反馈
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 1050 <= prices[i] <= 104
其实是一个分区域解决的问题。
买卖股票要分别选择低点和高点,而遍历数组的同时,也是寻找不同区域最低点和最高点的过程,比如遍历到第二个元素,就是在1,2两个元素中求出最低点和最高点,而后推移遵循的原则是:遇到更低的点替换最低点,遇到更高的点做差看是否能获得更大利润。
class Solution {
public:
int maxProfit(vector& prices)
{
int ans=0;
int mintemp=prices[0];
for(int i:prices)
{
if(ians)
ans=i-mintemp;
}
return ans;
}
}; 566. 重塑矩阵
难度简单312收藏分享切换为英文接收动态反馈
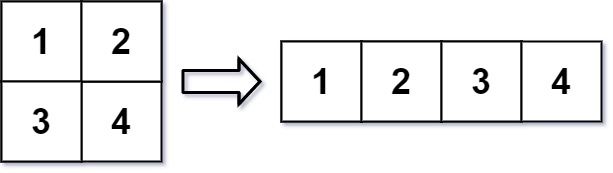
在 MATLAB 中,有一个非常有用的函数 reshape ,它可以将一个 m x n 矩阵重塑为另一个大小不同(r x c)的新矩阵,但保留其原始数据。
给你一个由二维数组 mat 表示的 m x n 矩阵,以及两个正整数 r 和 c ,分别表示想要的重构的矩阵的行数和列数。
重构后的矩阵需要将原始矩阵的所有元素以相同的 行遍历顺序 填充。
如果具有给定参数的 reshape 操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。
示例 1:
输入:mat = [[1,2],[3,4]], r = 1, c = 4 输出:[[1,2,3,4]]
示例 2:
输入:mat = [[1,2],[3,4]], r = 2, c = 4 输出:[[1,2],[3,4]]
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 100-1000 <= mat[i][j] <= 10001 <= r, c <= 300
一个对用vector表示二维数组的应用。
class Solution {
public:
vector> matrixReshape(vector>& mat, int r, int c)
{
if(mat.size()*mat[0].size()!=r*c)
return mat;
vector>remat(r,vector(c));
for(int i=0;i 118. 杨辉三角
难度简单779收藏分享切换为英文接收动态反馈
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
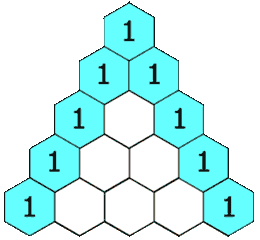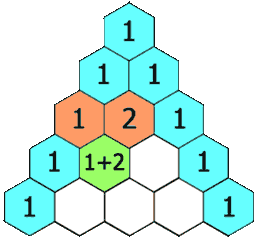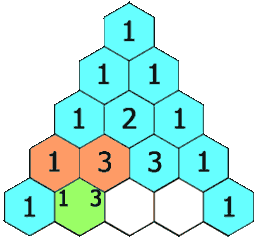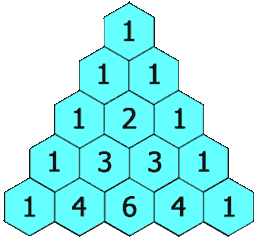
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
示例 1:
输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1 输出: [[1]]
提示:
1 <= numRows <= 30
模拟题,写出推理公式:
ret[i][j] = ret[i - 1][j] + ret[i - 1][j - 1];
洛谷的时候模拟题还挺多的...
class Solution {
public:
vector> generate(int numRows)
{
vector> ret(numRows);
for (int i = 0; i < numRows; i++)
{
ret[i].resize(i + 1);
ret[i][0] = ret[i][i] = 1;
for (int j = 1; j < i; ++j)
{
ret[i][j] = ret[i - 1][j] + ret[i - 1][j - 1];
}
}
return ret;
}
}; 36. 有效的数独
难度中等906收藏分享切换为英文接收动态反馈
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
注意:
- 一个有效的数独(部分已被填充)不一定是可解的。
- 只需要根据以上规则,验证已经填入的数字是否有效即可。
- 空白格用
'.'表示。
示例 1:
输入:board = [["5","3",".",".","7",".",".",".","."] ,["6",".",".","1","9","5",".",".","."] ,[".","9","8",".",".",".",".","6","."] ,["8",".",".",".","6",".",".",".","3"] ,["4",".",".","8",".","3",".",".","1"] ,["7",".",".",".","2",".",".",".","6"] ,[".","6",".",".",".",".","2","8","."] ,[".",".",".","4","1","9",".",".","5"] ,[".",".",".",".","8",".",".","7","9"]] 输出:true
示例 2:
输入:board = [["8","3",".",".","7",".",".",".","."] ,["6",".",".","1","9","5",".",".","."] ,[".","9","8",".",".",".",".","6","."] ,["8",".",".",".","6",".",".",".","3"] ,["4",".",".","8",".","3",".",".","1"] ,["7",".",".",".","2",".",".",".","6"] ,[".","6",".",".",".",".","2","8","."] ,[".",".",".","4","1","9",".",".","5"] ,[".",".",".",".","8",".",".","7","9"]] 输出:false 解释:除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
提示:
board.length == 9board[i].length == 9board[i][j]是一位数字(1-9)或者'.'
高强度模拟题了属于是
这里用三个数组分别判断满足数独的三种条件
class Solution {
public:
bool isValidSudoku(vector>& board)
{
int rows[9][9];
int cols[9][9];
int subb[9][9][9]; //三个数组分别验证三个条件
memset(rows,0,sizeof(rows));
memset(cols,0,sizeof(cols));
memset(subb,0,sizeof(subb));
for(int i=0;i<9;i++)
for(int j=0;j<9;j++)
{
char c=board[i][j];
if(c!='.')
{
int index=c-'0'-1; //额外-1,因为数组是0~9
rows[i][index]++;
cols[j][index]++;
subb[i/3][j/3][index]++;
if(rows[i][index]>1
||cols[j][index]>1
||subb[i/3][j/3][index]>1)
return false;
}
}
return true;
}
}; 73. 矩阵置零
难度中等736收藏分享切换为英文接收动态反馈
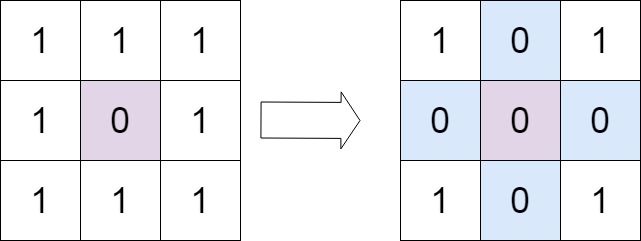
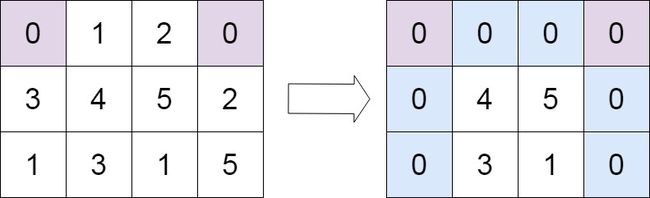
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1:
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] 输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-231 <= matrix[i][j] <= 231 - 1
进阶:
- 一个直观的解决方案是使用
O(mn)的额外空间,但这并不是一个好的解决方案。 - 一个简单的改进方案是使用
O(m + n)的额外空间,但这仍然不是最好的解决方案。 - 你能想出一个仅使用常量空间的解决方案吗?
采用先遍历一遍原数组,将数组中有0出现的行号,列号都记下来
之后二次处理进行置零的方法。
还有省空间复杂度的方法今天累了不想写了。。。
class Solution {
public:
void setZeroes(vector>& matrix)
{
vectorrow(matrix.size());//存储要清除的行号
vectorcal(matrix[0].size());//存储要清楚的列号
for(int i=0;i 写在最后:写这个总结好累啊(封面就放两张十元叭,累了难过,石原里美),以后一定要每天养成写题解的好习惯。不过这个过程也对各种算法思路,STL的使用更加熟悉了。
假期加油,冲冲冲