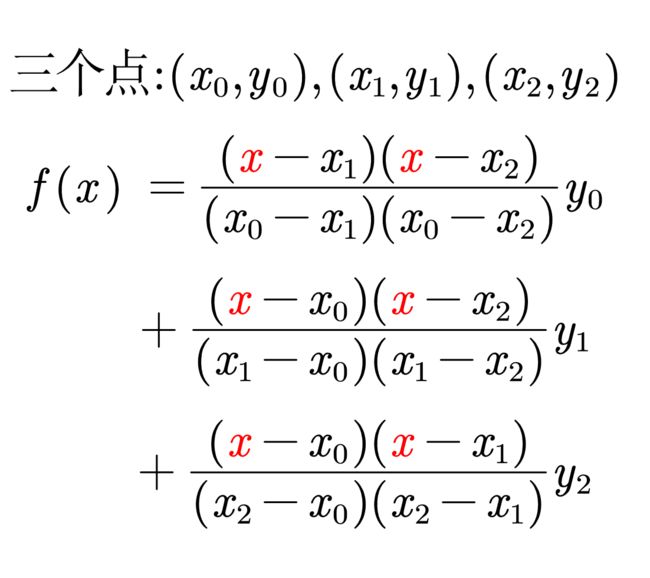数学建模笔记-第三讲-插值

插值

定义

分类

插值多项式

拉格朗日插值

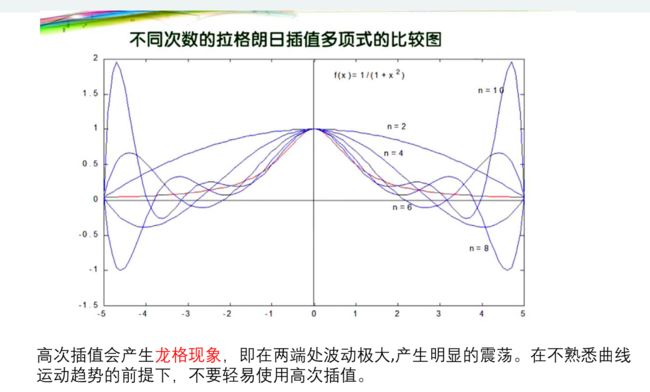
龙格现象

高次插值，两端波动大

牛顿插值

两种插值法对比

上述两种插值方法，仅满足了插值节点与被插函数的函数值相等没有考虑其导数值。

之后介绍埃尔米特插值法会改进这一点

分段插值

一个点，和其相邻的两个点，进行二次插值，取区间上的一段

一段又一段构成了总的插值函数

分段就是为了解决龙格现象

埃尔米特插值

不细讲原理
由于也存在龙格现象，于是加入分段插值的思想并实现

pchip(x,t,new_x)

返回new_x对应的插值的值

% 分段三次埃尔米特插值
x = -pi:pi; %d=1的等差数列
y = sin(x); 
new_x = -pi:0.1:pi;
p = pchip(x,y,new_x); % 插值后的结果
figure(1); % 在同一个脚本文件里面，要想画多个图，需要给每个图编号，否则只会显示最后一个图哦~
plot(x, y, 'o', new_x, p, 'r-') % x,y构成的点图，new_x与p（插值点和插值后的值）构成的线图

% plot函数用法:
% plot(x1,y1,x2,y2)  可以同时画两个函数
% 线方式： - 实线 :点线 -. 虚点线 - - 波折线 
% 点方式： . 圆点  +加号  * 星号  x x形  o 小圆
% 颜色： y黄； r红； g绿； b蓝； w白； k黑； m紫； c青
% 可以画点图，可以画线图，也可以点线结合

三次样条插值

还要求二阶连续可微，更光滑

不阐述原理

代码实现

spline(x,y,new_x)`

% 三次样条插值和分段三次埃尔米特插值的对比
x = -pi:pi; 
y = sin(x); 
new_x = -pi:0.1:pi;
p1 = pchip(x,y,new_x);   %分段三次埃尔米特插值
p2 = spline(x,y,new_x);  %三次样条插值
figure(2);  % 要单独命名图的标号，否则可能会覆盖前面的图
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')
legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast')   %标注显示在东南方向
% 说明：
% LEGEND(string1,string2,string3, …)
% 分别将字符串1、字符串2、字符串3……标注到图中，每个字符串对应的图标为画图时的图标。
% plot有三组函数（1个点图，2个线图），就给三个图例名字
%‘Location’用来指定标注显示的位置

结论

比赛时最常用的就是埃尔米特插值和三次样条插值，都是可以的。还可以求个平均值等等

n维数据插值（了解）

很少用，要有多组数据的时候才可能用

% n维数据的插值
x = -pi:pi; y = sin(x); 
new_x = -pi:0.1:pi;
p = interpn (x, y, new_x, 'spline');
% 等价于 p = spline(x, y, new_x);
figure(3);
plot(x, y, 'o', new_x, p, 'r-')

可以用于短期预测

建模时预测最好不要用插值。可以选择拟合算法或者专门的预测算法

% 人口预测（注意：一般我们很少使用插值算法来预测数据，随着课程的深入，后面的章节会有更适合预测的算法供大家选择，例如灰色预测、拟合预测等）
population=[133126,133770,134413,135069,135738,136427,137122,137866,138639, 139538];
year = 2009:2018;
p1 = pchip(year, population, 2019:2021)  %分段三次埃尔米特插值预测
p2 = spline(year, population, 2019:2021) %三次样条插值预测
figure(4);
plot(year, population,'o',2019:2021,p1,'r*-',2019:2021,p2,'bx-')
legend('样本点','三次埃尔米特插值预测','三次样条插值预测','Location','SouthEast')

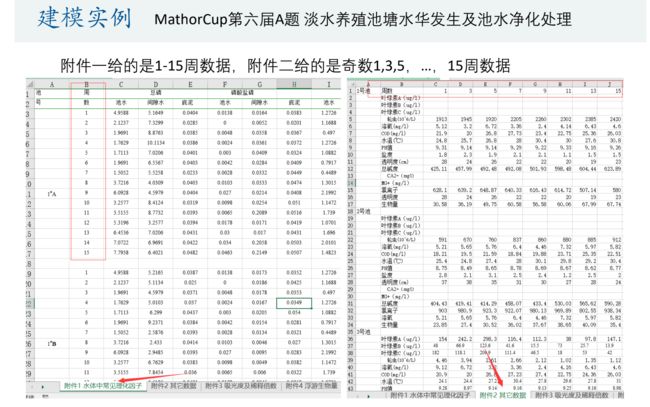
建模实例

数据只有单周的，要补全，就可以选择插值

可不可以选择拟合？

拟合相比插值，是不需要一一对应，拟合出来的曲线不用经过所有点。只用在一定精度下尽可能接近就行。

拟合有一个条件是样本点要比较多，而这里只有8个样本点，就更适合插值

本笔记来自清风老师的数学建模，强烈推荐该课程！