BZOJ 1040 骑士（树形DP）

题目链接：http://61.187.179.132/JudgeOnline/problem.php?id=1040

题意：给出一个图，只有一个环。每个点有一个权值。选出一些点两两不相邻，使得权值最大？

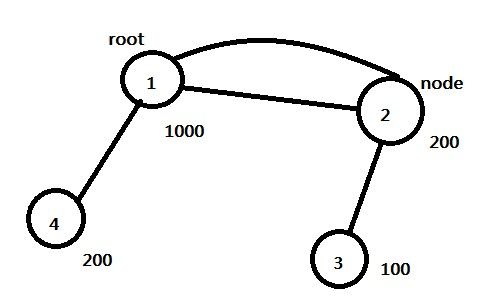
思路：（1）找到环。DFS，标记访问，下一个节点不是父节点但是已被访问则这条边就是环上的两个点。标记这个边是我们找到的环边，并将这两个点的中一个设置为root，另一个我们设为node；

（2）由于root和node不能同时选，我们一次将root设置为不能选node随意；另一次将node设置为不能选root随意，这样树形DP两次。注意在遇到（1）中标记的环边时不能走。这里注意不是root走到node不能走，是只有遇到这个环边的才不能走。比如下图，我们若是root到node都不能走，则答案显然是错误的；所以我们应该标记环边不能走 。

#include <iostream>
#include <cstdio>
#include <string.h>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <set>
#include <stack>
#include <string>
#include <map>


#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)<(y)?(x):(y))
#define abs(x) ((x)>=0?(x):-(x))
#define i64 long long
#define u32 unsigned int
#define u64 unsigned long long
#define clr(x,y) memset(x,y,sizeof(x))
#define CLR(x) x.clear()
#define ph(x) push(x)
#define pb(x) push_back(x)
#define Len(x) x.length()
#define SZ(x) x.size()
#define PI acos(-1.0)
#define sqr(x) ((x)*(x))
#define MP(x,y) make_pair(x,y)

#define FOR0(i,x) for(i=0;i<x;i++)
#define FOR1(i,x) for(i=1;i<=x;i++)
#define FOR(i,a,b) for(i=a;i<=b;i++)
#define FORL0(i,a) for(i=a;i>=0;i--)
#define FORL1(i,a) for(i=a;i>=1;i--)
#define FORL(i,a,b)for(i=a;i>=b;i--)


#define rush() int CC;for(scanf("%d",&CC);CC--;)
#define Rush(n)  while(scanf("%d",&n)!=-1)
using namespace std;


void RD(int &x){scanf("%d",&x);}
void RD(i64 &x){scanf("%lld",&x);}
void RD(u64 &x){scanf("%I64u",&x);}
void RD(u32 &x){scanf("%u",&x);}
void RD(double &x){scanf("%lf",&x);}
void RD(int &x,int &y){scanf("%d%d",&x,&y);}
void RD(i64 &x,i64 &y){scanf("%I64d%I64d",&x,&y);}
void RD(u32 &x,u32 &y){scanf("%u%u",&x,&y);}
void RD(double &x,double &y){scanf("%lf%lf",&x,&y);}
void RD(int &x,int &y,int &z){scanf("%d%d%d",&x,&y,&z);}
void RD(i64 &x,i64 &y,i64 &z){scanf("%I64d%I64d%I64d",&x,&y,&z);}
void RD(u32 &x,u32 &y,u32 &z){scanf("%u%u%u",&x,&y,&z);}
void RD(double &x,double &y,double &z){scanf("%lf%lf%lf",&x,&y,&z);}
void RD(char &x){x=getchar();}
void RD(char *s){scanf("%s",s);}
void RD(string &s){cin>>s;}


void PR(int x) {printf("%d\n",x);}
void PR(int x,int y) {printf("%d %d\n",x,y);}
void PR(i64 x) {printf("%lld\n",x);}
void PR(u32 x) {printf("%u\n",x);}
void PR(u64 x) {printf("%I64u\n",x);}
void PR(double x) {printf("%.6lf\n",x);}
void PR(char x) {printf("%c\n",x);}
void PR(char *x) {printf("%s\n",x);}
void PR(string x) {cout<<x<<endl;}


const int mod=12345678;
const i64 inf=((i64)1)<<60;
const double dinf=1e50;
const int INF=2000000005;
const int N=1000005;


i64 a[N],f[N][2];
int n;
vector<pair<int,int> > g[N];
int h[N],node,root,t;


void DFS(int u,int pre)
{
    h[u]=1;
    int i,v;
    FOR0(i,SZ(g[u]))
    {
        v=g[u][i].first;
        if(v==pre) continue;
        if(h[v])
        {
            node=u; root=v; t=g[u][i].second;
            continue;
        }
        DFS(v,u);
    }
}


int flag;


void DP(int u,int pre)
{
    f[u][0]=f[u][1]=0;
    int i,v;
    FOR0(i,SZ(g[u]))
    {
        v=g[u][i].first;
        if(g[u][i].second==t||v==pre) continue;
        DP(v,u);
        f[u][0]+=max(f[v][0],f[v][1]);
        f[u][1]+=f[v][0];
    }
    f[u][1]+=a[u];


    if(u==root&&flag==0) f[u][1]=0;
    if(u==node&&flag==1) f[u][1]=0;
}


int main()
{
    RD(n);
    int i,x,id=0;
    FOR1(i,n)
    {
        RD(a[i]);
        RD(x); id++;
        g[i].pb(MP(x,id)); g[x].pb(MP(i,id));
    }
    i64 ans=0,temp;
    FOR1(i,n) if(!h[i])
    {
        node=0; DFS(i,0);
        flag=1;  DP(root,0);
        temp=max(f[root][0],f[root][1]);


        flag=0;  DP(root,0);
        temp=max(temp,max(f[root][0],f[root][1]));
        ans+=temp;
    }
    PR(ans);
    return 0;
}