魔方还原算法(一) 概述

写在前面

我最初接触魔方的时候是在初二，那时不知是谁先起的头，然后全班都开始玩。我也不例外，花了一晚上学了学层先法，层先法挺简单的，只有几个公式，一晚上就会了。从那时起我也是能够复原魔方的人了，但是层先法复原魔方速度很慢，到了高中又学了学 CFOP 这个高级还原公式，速度提升很多。我玩魔方吧也没想过去拼什么段位追求 sub 几几几，就一业余爱好，魔方随时放在旁边，兴起时就转两把。

而最近开始写公众号，一直想写点不一样的，然后就瞄准了魔方，关于魔方的研究国内其实不少，但数学偏多，有关计算机方面讲述还原算法的文章几乎没有，有也只是概述，看了之后可能感觉还是云里雾里，只能从上层抽象的角度得到一个基本认识。

本系列文章就来弥补这个缺口，详细的讲讲经典的魔方还原算法是怎样的。魔方就是个数学问题，主要是离散的群论部分，研究魔方肯定也绕不开数学，但鉴于本人数学水平并不高，大家肯定也不太喜欢文章里面一大堆数学公式证明过程，所以采取折中的方法，涉及到数学的地方咱们只做 “严谨的定性解释”，如果有什么错误还请批评指正。

第一篇知识概述介绍，没有太多实际的算法部分，主要是讲述魔方的一些特性，讲述的也是狭义上的魔方，也就是最常见的三阶魔方，下面来看正文。

魔方介绍

魔方还需要介绍？这是给不熟悉魔方的朋友说的，熟悉的大佬可以跳过。再者要先说点轻松的，放松放松，否则一来就正餐的话，你这个聪明的小脑瓜也可能一时半会也转不过来。内容都分了小标题，熟悉的部分可以选择性的跳过。

简述历史

魔方，又叫鲁比克方块，是一位匈牙利的建筑学和雕塑学教授鲁比克·艾尔诺，为了帮助学生们认识空间立方体的组成和结构而发明的一种益智玩具，其灵感来自多瑙河中的沙砾。

魔方在今天似乎玩的人不太多，至少我感觉周围没有多少，但在地铁公交等地儿也可能偶遇大佬。魔方真正风靡全球，广为大众喜爱是在上世纪 80 年代，据估计全球有五分之一的人在玩魔方。五分之一呢，可以想象魔方曾火爆到什么程度。

魔方发展至今，已经有了许多不同的变化，有着各种不同的形状样式，玩法也千奇百怪，速拧，盲拧，克隆等等，节目最强大脑曾经还出现过听音辨位这种变态盲拧复位(???)

基本常识

基本组成

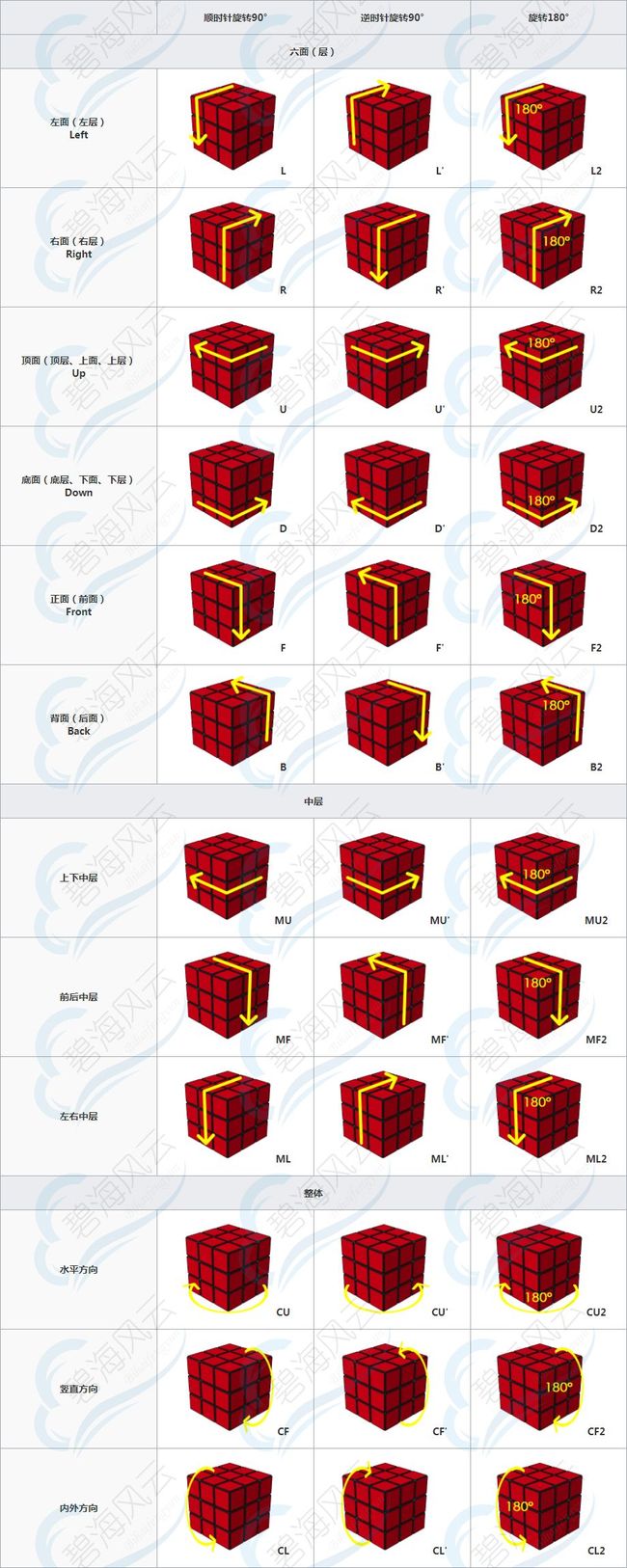
三阶魔方有 $6\times 9=54$ 个面，或者整体来看有 上下左右前后 6 个面，为做区分，这里称为层。上下左右前后 6 个面/层分别命名为 U, D, L, R, F, B，也就是对应英文单词的首字母，看下图，3D 图画得很烂还请见谅

有 8 个角块，每个角块 3 个面，12 个棱块，也叫棱边/边，每个棱块 2 个面。还有 6 个中心块，只有 1 个面。转动魔方会引起角块棱块位置变化，角块只能移动到角块，棱块只能移动到棱块。角块用它的三个面来命名，棱块同样的用它的两个面来命名，举个例子如下所示：

这两个块分别叫做角块 URF ，棱块 UR 。

辛马斯特标记(Singmaster Notation )

英国原伦敦南岸大学数学教授大卫·辛马斯特（David Breyer Singmaster），在研究魔方问题的同时，于1978年12月发明了魔方转动的记录方法，称之为“辛马斯特标记”（Singmaster notation），此后便成为了通用标准，也就是俗称的“公式符号”。

找了一张很详细的图来说明什么意思，看下图：

在本列些文章里只用到前 6 行 的18 种基本转动，也就是不予考虑后面的中层转动和体转，体转会用到部分，在下篇讲算法种用到。在研究魔方一般不予考虑中心块的位置和中间层的转动，将 6 个中心块的位置视为不变作为参考系，而中间层的转动是可以用其他两层的转动来替代的，所以两者都不予考虑变化。

记步方式

1. HTM：Half Turn Metric，任意层的任意转动记为一步
2. QTM：Quarter Turn Metric，90°的转动才记作一步，180°的转动记为两步

还有其他的记步方式不说明了，最主要的就是这两种记步方式，本系列文章所用的记步方式为 HTM，本文用不到，下篇文章会用到，本文只是做介绍。

复原方法

层先法

魔方复原一种方法，几乎是所有玩魔方的人首先使用的还原方法，恰如其名，指的是分底层中层顶层来复原魔方。

CFOP

使用层先法复原魔方很慢，当然如果你手速够快也能很快复原，据说菲神使用层先法也能sub10？当然对于我们普通人来说想要提高除了手速，那就是换用更高级的公式，一般来说就是 CFOP 公式。

1. Cross ：底层十字，无公式，按经验来，高手一般都是 7 步以内

2. F2L：First two Layer：同时复原前两层，41 个公式

3. OLL：Orient Last Layer：复原顶层，只是顶面的颜色复原了，位置没有复原，57个公式

4. PLL：Permutation of Last Layer：调整棱块角块位置，完全复原顶层，21 个公式

GOD

上帝之数

上帝之数指的是还原一个任意打乱的魔方需要的最少步数。关于上帝之数的寻找持续了 30 多年，最终在 2010 年，几位数学家通力合作在谷歌帮助下证明三阶魔方的上帝之数为 20。20 为采用HTM记步方式得到的步数，若采用 QTM 为 26。

关于上帝之数的研究不多说，有一篇很好的文章，感兴趣的可以看看，是卢昌海写的一篇博客 魔方与 “上帝之数”

上帝算法

任意给定一个魔方状态，上帝总能使用最少的步数来复原魔方，而上帝还原魔方的方法就叫做上帝算法。

这种算法存在吗？答案是存在的，我们会在后面的文章详细讲述。在这儿简单聊聊，想想上帝算法应该是怎样的，**要想得到步数最短的解法，说明在每个状态下所做的决策都会向还原状态靠近。**也就是说不论魔方处于什么状态，上帝算法都能给出下一步转动的方案，且这个转动能够使当前状态距离还原状态更近一步。

恶魔算法

有一个转动序列，如果重复操作能够遍历魔方的所有状态，那么对于任意一个魔方状态，我们都可以应用这个转动序列使魔方达到还原状态，这就是恶魔算法。私以为其实也可以叫做万能算法吧，不管什么状态，只要一直这么转就能转到还原状态。

恶魔之数

这个恶魔之数不是 666 啊，而是指上面所说的那个转动序列最少步数是多少。前面提到过魔方是一个置换群，应用任意一个转动序列，已证明最多重复 1260 次便可以将魔方带到初始状态(不是还原状态)中去。所以恶魔之数是可以算出来的，为总的状态数除以 1260，等于 34,326,986,725,785,601。

为什么要用总的状态数来除以 1260，重复一个转动序列就能将任意状态给带回还原状态，是不是也就意味着只要重复这个转动序列就能遍历所有的魔方状态，而恶魔之数要求这个转动序列最短，所以总的状态数除以最大周期数 1260。但这个数太大太大，所以要找到这么一个转动序列几乎不可能。

魔方状态数

第一个有点烧脑的地方来了，魔方魔方，它有多少种不同的状态呢？有关注过魔方的魔友应该对着很熟悉，网上的解答解析也很多，但私以为绝大部分都没有从头至尾的说清楚，只是说明了一个大概，这小节就魔方状态数的问题从头至尾的详细说明一些魔方中的定律，希望能助你完全理解这个状态数是怎么算出来的。其中不可避免的用到一些数学知识，前面说过鉴于本人数学太菜，各位应该也不希望看到满是数学证明的公式符号，所以折中一下，采用“严谨的定性解释”来说明。

抛开限制的状态数

首先我们抛开各种限制条件来粗略的算一下魔方的状态数，这就变成了一个稍稍难了那么一点的排列组合问题，一起来看看：

角块有 8 个，所以有 8！个位置排列，每个角块会有 3 种方向，8 个角块就有 3⁸ 种方向排列，因此关于角块总的状态为 $8! \times 3^8 $

棱块有 12 个，所以有 12！个位置排列，每个棱块有两种方向，12 个棱块就有 2¹² 方向排列，因此关于棱块总的状态为 $12!\times 2^{12}$

所以抛开限制条件魔方总的状态数为

$$8!\times 3^8\times 12!\times 2^{12}=519,024,039,293,878,272,000$$

虽然这个数是咱们抛开限制条件粗略算出的一个数，但也是有实际意义的，这个数就是你把魔方大卸八块拆了之后，共有多少种方式装回去。

限制条件

那这个限制条件是什么呢？其实就是魔方的转动——合法的魔方转动。魔方转动的一个基本操作就是某个面转动 90°，它限制了角块只能移动到角块，棱块只能只能移动到棱块，而且每次转动就会有 4 个角块，4 个棱块的位置发生变化。我们可以把魔方一个面的基本转动可以看做原子操作，要么全做，要么不做。也就是说只要转动某个面，那就一定有上述的变化，而且是全套的，不可能只有某些块发生变化。

必要数学知识

用到的一些离散数学知识：

1. 魔方就是一个群，而且是一个置换群。

2. 两元素相互交换叫做对换，由偶数次对换得到的置换叫做偶置换，由奇数次对换得到的置换叫做奇置换。

3. 所有置换可以分为个数相等的奇置换和偶置换，任意一个置换可以分解成多个对换之积。

4. 偶 偶 = 奇，奇 奇 = 偶，奇 偶 = 奇，偶 奇 = 奇。偶置换复合偶置换还是偶置换，奇置换复合奇置换变成偶置换，奇偶置换复合结果是奇置换。

没学过离散的朋友们来看看这个例子，来简单了解一下：

上图中讲述两个排列怎么发生的置换操作，应该很清楚明了了，这在数学中记为$\left(\begin{array}{cccc}1& 2& 3& 4\\ 4& 1& 2& 3\end{array}\right)=(12)(13)(14)$，表示这个置换可以分解成 3 次对换，所以是一个奇置换。也可以这么看，只经过一次对换操作是奇置换，上述置换由 3 个奇置换复合，所以合起来也为奇置换。有了这基本认识之后，我们来看看因为魔方基本转动所带来的一些性质或者说约束。

三约束

位置

上述有 4 个角块 4 个棱块发生了变化，分开来看的话是不是与上述的 4 个数的置换一样的？所以角块的置换可以分解成 3 个对换为一奇置换，同样的棱块的置换可以分解成 3 个对换也为一奇置换，合起来发生了 6 次对换为一偶置换。

这也就是网上许多解析上说不可能只交换一对色块的原因所在，单独的只交换一对色块因为只交换了一次是一个奇置换，是不可能靠正常的转动得到的。

置换群里面奇置换和偶置换的个数是相等的，为什么相等不做证明了，自行百度，所以合法的置换只占一半。因此如果你把魔方拆开再随意组装的话，只考虑位置的情况下只有 $\frac{1}{2}$ 的几率组装正确。

方向

关于方向的问题就没那么简单了，也不是说有多困难，而是方向不像位置那样直观。如果一个角块或者棱块在它们的本来位置(复原时所处的位置)，我们能够很容易的去定义它们的方向，比如下图所示：

图中所示的魔方状态中各个块的位置都处在复原位置，只有方向不对头，角块 UFL 顺时针旋转了120°，UBR逆时针旋转了120°。棱块FR，FD 呈翻转状态。

但是当块/边没在复原位置呢？我们怎么去定义方向？这个方向如何去量化？这时就需要定义一个标准，这里介绍科先巴的二阶段算法(咱们后面文章会讲的还原算法之一)中的定义方法:

先来说说棱块，棱块比较简单，只有两个方向也就是翻转未翻转两个状态，我们可以用 0，1 来表示。0 表示未翻转，如上图的棱块UR，1 表示翻转，如上图中的棱块 FR。科先巴的算法里面规定只有 F，B 层的转动会改变棱块的方向，其他层 U D L R 的转动并不改变棱块的方向。标准定义只要合理即可，你可以选择任意两个相对的面来替代 F，B，甚至可以定义六个面的转动都会改变棱块的方向。

角块有 3 个方向，需要用 3 个数 0,1,2 来表示。0 表示未发生扭转，1 表示顺时针扭转，2 表示逆时针扭转。每个角块都有一个 U 层或者 D 层的面，只要这个面处在 U 层或者 D 层就表示未扭转，方向值为 0 。如果角块拥有的是 U 层面，即使处在 D 层也代表未扭转，方向值为 0，反之亦然。

注意是根据角块当前所处的位置而不是它的复原位置来确定是否扭转，也就是说不论角块拥有的是 U 层面还是 D 层面，将它目前所处的 U/D 层作为标准。用下图来具体说明：

URF 这个位置上的块拥有 U 层面(蓝色属于U层)处在 U 层以 U 层为标准，顺时针扭转，方向值为 1；ULF 这个位置上的块拥有 D 层面(绿色属于D层)处在 U 层以 U 层为标准，逆时针扭转，方向值为 2；因此 U，D 层的转动不会改变角块的方向，只有其它层 L，R，F，B 的转动才会改变角块的方向。

接下可以回到约束上面，关于方向问题依然可以按照群的理论来考虑，方向约束分又为角块方向和棱块方向约束，分别来看：

棱块方向

由上所知，L，R，F，B 的转动不会翻转棱块，也就是翻转了 0 个棱块，翻转了偶数个棱块；F，R的转动翻转 4 个棱块，亦翻转了偶数个棱块。所以不论怎么转动，总的翻转数应该为偶数个，所有的棱块方向值的和为 2 的倍数。翻转奇数个棱块，所有棱块方向值的和非 2 的倍数都是不可能的。

角块方向

角块的方向就不太好用扭转的个数来看，因为有两种顺时针和逆时针两种扭转方式，最好是用方向值的和来描述。咱们从复原状态开始考虑，这时角块的方向值和为 0 。若 U，D 层转动，角块方向值不变，和为 0 是 3 的倍数。若 L，R，F，B 某一层转动，有两个角块顺时针转动，另外两个角块逆时针转动(前一小节只描述了两个角块，可以看看另外两个角块会发现的确是这样)，所以方向值的总和变为$1+2+1+2=6$ 同样为 3 的倍数。不论怎么转动，它都是单层基本转动的复合，因此所有角块的方向和应该为 3 的倍数。所以如果单独扭转一个角块，所有角块方向值总和只改变 1 或 2，使其不再是 3 的倍数，正常情况下这是不可能出现的。

不论是国内网站还是国外网站大多都解释到这一步，只是告诉你因为不可能单独翻转一个棱块，所以在任意组装魔方时只有 $\frac{1}{2}$ 的几率棱块方向是正确的；也不可能单独扭转一个角块，所以只有 $\frac{1}{2}$ 的几率角块的方向是正确的。不知道是不是因为我的理解能力有欠缺，对这么直接解释有些接受不了，不可能单独扭转一个角块我知道，可是为啥在组装魔方时就只有 $\frac{1}{3}$ 的几率角块方向正确了呢？

思考之下，我有了以下简单证明，拿角块的方向举例：

在将魔方大卸八块之后任意组装 8 个角块，不考虑位置，只考虑方向，每个块的方向我们有 3 种取值，分别为 0，1，2。所以这其实可以变做一个数学题，从集合$\{1,2,3\}$ 中随机抽取一个数，抽取 k(8) 次，计算这 k 个数的和，证明和为 3 的倍数的概率为 $\frac{1}{3}$，和模 3 之后余 1 余 2 的概率也都为 $\frac{1}{3}$ 。

这问题用数学归纳法是很好证明的，$n=1$ 时，显然成立；假设 $n=k-1$时也成立；

那么 $n=k$ 时，若$S_{k-1}mod3=0$，则第 n 次只能取 0 才能够使和为 3 的倍数，若$S_{k-1}mod3=1$，则第n次只能取 2 才能够使和为 3 的倍数，若$S_{k-1}mod3=2$，则第 k 次只能取 1 才能使和为 3 的倍数。

所以不论 $S_{k-1}$ 值为多少，$S_{k-1}+a_k$ 的和是 3 的倍数概率都是 $\frac{1}{3}$ ，则 $n=k$ 时也成立。

所以任意组装魔方，8 个角块方向组装正确的概率是 $\frac{1}{3}$，关于棱块方向就同理不赘述了。

三阶魔方状态数

有了解上述内容之后，正确的状态数应该很容易计算了，就是在我们最开始计算的状态数再除以 12 就行了，也就是说任意组装一个魔方只有 $\frac{1}{12}$ 的概率是正确的。

因此总的状态数为$$\frac{8!\times 3^8\times 12!\times 2^{12}}{3\times 2\times 2}=43,252,003,274,489,856,000$$

网上还流传着一种算法，本质上都差不多，也再简单说说吧：

角块方向：当 7 个角块方向确定的时候，最后一个角块的方向也唯一确定了，因为不可能单独扭转一个角块，所以角块方向数$3^7$。

棱块方向：当 11 个棱块方向确定的时候，最后一个棱块的方向也唯一确定了，因为不可能单独翻转一个棱块，所以棱块方向数为$2^{11}$。

位置的计算方法同前，总数为 $\frac{8!\times 12!}{2}$ 。

因此总的状态数为$$\frac{8!\times 3^7\times 12!\times 2^{11}}{2}=43,252,003,274,489,856,000$$

为什么当 7 个角块方向确定的时候，第 8 个角块方向也就唯一确定了？这儿可以用反证法，如果 7 个角块定了之后，第 8 个角块方向没定，那是不是说明第 8 个角块还可以扭转，正常情况下这是不被允许的，出现矛盾，即证。棱块的方向也同理。还有非正常情况？嗯没错，就是你想的那样，干过这种事吧，硬掰一个角。

结尾

魔方还原算法(一)主要内容就结束了，其实并没有涉及到多少算法内容，主要是对魔方做一些基本介绍，借着计算魔方状态数来说明了魔方问题中的一些定理或者说本身存在的约束。

关于方向定义那一块也相当于对科先巴的二阶段算法开头了，下篇文章将做具体介绍。在所有魔方还原算法中，最出名的应该就是科先巴的二阶段算法，大家可以先想想如果让你设计一个还原算法，你会怎么设计，暴力搜索？还真没错，就是暴力搜索，本质上所有的还原算法都是暴力搜索，就连上帝之数 20 那也是暴力搜索搜出来的。暴力搜索也有技巧，需要考虑怎么更有效率，这就涉及到以下几个关键问题：

1. 如何定义一个魔方？
2. 如何定义转动操作？
3. 怎么根据魔方的特殊性省时省空间？
4. 如何剪枝？
5. 使用什么搜索算法？

也就是说怎么组织数据结构，使用什么搜索算法更优效率，也就应证了那句话 $数据结构+算法=程序$ 。

本文就到这儿了，下篇我们再继续，本号没有留言功能，欢迎大家加我微信进行交流，有什么错误的地方还请批评指正。