二 . LeetCode标签刷题—— 二分法（二分搜索算法） 部分

做新题，如果之前也有类似的题，多了就去掉，少了就补上

二分法的流程：

确保问题答案具有二段性（95%以上），另外还有5%的题目虽然不具有二段性，但仍可以使用二分法，例如每次都可以把区间缩小一半。

check是二分的边界条件。

33. 搜索旋转排序数组

题目

升序排列的整数数组 nums 在预先未知的某个点上进行了旋转（例如， [0,1,2,4,5,6,7] 经旋转后可能变为 [4,5,6,7,0,1,2] ）。

请你在数组中搜索 target ，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4
示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1
示例 3：

输入：nums = [1], target = 0
输出：-1

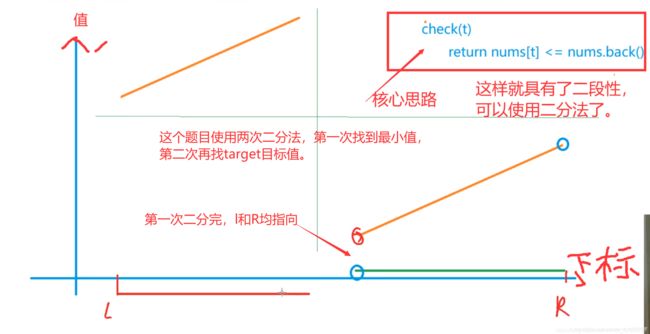
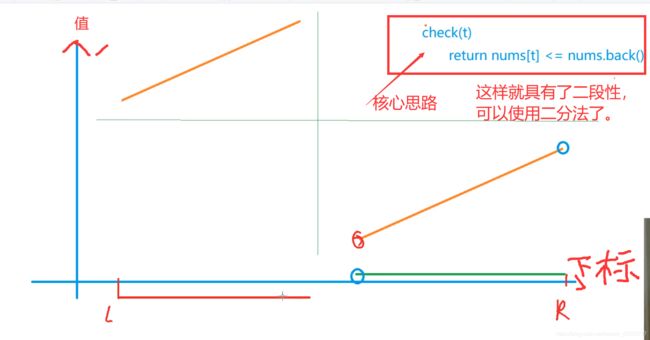
这个题目使用两次二分，第一次和上一题一样找到数组最小值，第二次二分是想找到target值。

代码：

class Solution {
public:
    int search(vector<int>& nums, int target) {
        if(nums.empty())return -1;    //数组判空，看题目要求，有的需要判断，有的不需要。

        int l=0,r=nums.size()-1;    //第一次二分，找到数组最小值，和上一题思路相同。
        while(l<r){
            int mid=(l+r)>>1;	//注意除以2是右移1位，不是左移，
            if(nums[mid]<=nums.back()) r=mid;
            else l=mid+1;
        }
        
        if(nums.back()>=target) r=nums.size()-1;      //两种情况，第一种：target在后半段里，让l不变，r变成nums.size()-1;
        else l=0,r--;   //第二张情况：target在前半段里面，让l变成0，r变成r-1  (注：yi);

        while(l<r){     //第二次二分，要找target所在位置，
            int mid=(l+r+1)>>1;		//注意：不写+1的话，当 l = r - 1的时候就会死循环
            if(nums[mid]<=target) l=mid;
            else r=mid-1;
        }

        if(target==nums[l]) return l;   //最后找到target所在位置，返回target所在数组下标。注意target不一定存在于数组中，所以这里我们需要先判断一下再返回
        else return -1; //不存在，返回-1；

    }
};

方式二：以nums[0]作为分界条件。

class Solution {
public:     //先把题目搞懂让干嘛的再说（这个题目是让我们在一个原先升序后经一次旋转得到的数组中寻找是否存在一个目标值target）。
    int search(vector<int>& nums, int target) {
        if(nums.size()==0) return -1;
        int l=0,r=nums.size()-1;
        while(l<r){ //第一次二分要划分两个区间，第一个区间都满足>=nums[0]，第二个区间都<=nums[0];我们要找到满足>=nums[0]的最后一个数。
            int mid=(l+r+1)>>1;
            if(nums[mid]>=nums[0])l=mid;
            else r=mid-1;
        }
        //while循环完,l和r均指向了最后一个>=nums[0]的数
        if(target>=nums[0]) l=0;//即若target目标值在第一个区间的话,就让左区间l更新为0,r不变；
        else l=r+1,r=nums.size()-1;//否则的话，即若target目标值在第二个区间，就让左区间l更新为第二个区间的左端点，r更新为尾端点。
        while(l<r){ //第二次二分，在两个区间中的一个寻找target目标值。
            int mid=(l+r)>>1;  //下面就是经典二分的过程。
            if(nums[mid]>=target)r=mid; 
            else l=mid+1;
        }
        //while循环完，要么找到target（此时l或者r的位置即是所求），要么没有找到target，返回-1即可。
        if(nums[r]==target) return r;    //nums数组中存在target，即找到了target所在位置，就将target所处位置l或者r返回即可。
        else return -1;
    }
};

2021年8月15日12:11:12：

//二分法，见上图的分析
class Solution {
    public int search(int[] nums, int target) {
        if(nums.length==0) return -1; //先判空
        //第一次使用二分法，找到两段的分界点
        int l=0,r=nums.length-1;  //二分法的左右边界
        while(l<r){ //二分法的迭代条件，当l==r时结束迭代
            int mid=(l+r+1)>>1; //求出中点
            if(nums[mid]>=nums[0]) l=mid;   //更新l或者r
            else r=mid-1;
        }

        //结束上面的while二分，就可以找到两段的分界点,准备进行第二次二分，先找出来第二次二分的左右边界
        if(target>=nums[0]) l=0;  //注意这里要用nums[0]和target比较，这样可以不用考虑太多的边界情况了，如果是target>=nums[0],即在第一段，更新l=0
        else {  //否则在第二段，更新l=r+1,r=nums.length-1
            l=r+1;  //注意这里如果数组仍是有序的情况，则l就会是等于nums.length,即不会进入下面的while循环，则在执行if(nums[l]==target)的时候就会下标越界
            //所以下面的if(nums[l]==target)建议写成if(nums[r]==target)这样就不会出现下标越界的异常了。
            r=nums.length-1;
        }
        //第二次二分法
        while(l<r){
            int mid=(l+r)>>1;
            if(nums[mid]>=target) r=mid;
            else l=mid+1;
        }

        if(nums[r]==target)  return r;  //注意这里不要写if(nums[l]==target) return l,这样写的话有下标越界的可能
        else return -1;
    }
}

34. 在排序数组中查找元素的第一个和最后一个位置

题目

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

进阶：

你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗？

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]
示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]
示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

本题使用两次二分法，第一次使用二分法是为了找到第一个值等于target的下标，第二次使用二分法是为了找到最后一个值等于target的下标。

代码：

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        if(!nums.size()) return {-1,-1};    //如果数组为空，返回{-1，-1}；
        //或者：if(nums.empty()) return {-1,-1};

        int l=0,r=nums.size()-1;
        while(l<r){
            int mid=(l+r)>>1;
            if(nums[mid]>=target) r=mid;  //第一次使用二分法，是为了找到第一个值等于target的下标；
            else l=mid+1;
        }
        if(nums[l]!=target) return {-1,-1};  //此时l，r已经达到了最终位置，如果nums[l]!=target,说明数组中不存在等于target的数，返回{-1，-1}，结束循环；
        int start=l;  //否则，即找到了数组中等于target的数，用start记录其下标。

        l=0,r=nums.size()-1;
        while(l<r){
            int mid=(l+r+1)>>1;
            if(nums[mid]<=target) l=mid;   第二次使用二分法，是为了找到最后一个值等于target的下标；
            else r=mid-1;
        }
        int end=l;  //即找到了最后一个，数组中等于target的数，用end记录其下标。
        return {start,end};   //返回下标。
    }
};

2021年8月15日14:39:25：

利用二分思想先找其左边界，再找其右边界即可，注意找左边界的时候，由右侧逼近；找右边界的时候，由左侧逼近，即可。

//二分法，分开找两个端点，注意check函数的确定，
class Solution {
    public int[] searchRange(int[] nums, int target) {
        if(nums.length==0) return new int[]{-1,-1};
        int l=0,r=nums.length-1;  //一定要注意r更新是n-1,不是n
        while(l<r){
            int mid=(l+r)>>1;
            if(nums[mid]>=target) r=mid;  //左端点右边的数都满足这个性质，为了找到最左边的，我们需要往左找，即更新r=mid
            else l=mid+1;
        }
        if(nums[r]!=target) return new int[]{-1,-1}; //提前判断一下是否存在target这个数，如果不存在就提前结束
        int a=r;   //否则就先记录下来target的第一个位置
        r=nums.length-1;
        while(l<r){
            int mid=(l+r+1)>>1;
            if(nums[mid]<=target) l=mid;  //同上分析
            else r=mid-1;
        }
        return new int[]{a,r};
    }
}

35. 搜索插入位置

题目

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

示例 1:

输入: [1,3,5,6], 5
输出: 2

代码：

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        if(!nums.size()||nums.back()<target) return nums.size();  //nums为空，返回0，nums最后一个数仍然小于target，则返回n.
        int l=0,r=nums.size()-1;  //确定左右边界。
        while(l<r){
            int mid=l+r>>1;
            if(nums[mid]>=target) r=mid;   //自己画图理解，很简单
            else l=mid+1;
        }
        return l;
    }
};

2021年8月15日15:18:03：

class Solution {
    public int searchInsert(int[] nums, int target) {
        int n=nums.length;
        if(n==0) return 0;  //如果数组为空，需要特判
        //把需要特判左右边界的情况写到前面
        if(target<nums[0]) return 0;  //数组是有序的，所以我们可以直接把两种特殊情况写到前面
        if(target>nums[n-1]) return n;
        //否则就是经典的二分法的过程，
        int l=0,r=n-1;
        while(l<r){
            int mid=(l+r)>>1;
            if(nums[mid]>=target) r=mid;
            else l=mid+1;
        }
        return r;   //就算target不存在于数组中，l和r最后也会到达target应该插入的位置
    }
}

69. x 的平方根

题目

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2

代码：

class Solution {
public:
    int mySqrt(int x) {
        int l=0,r=x;   //先确定左右边界，
        while(l<r){
            int mid=(l+(long long)r+1)>>1;   //因为r可能为最大整数，所以结果可能溢出，						     加上long long限制。
            if(mid<=x/mid) l=mid;     //自己画图理解，mid小于待求的，所以l=mid,注意上一步要加1.
            else r=mid-1;
        }
        return l;  //返回l和r均可，此时l和r相等。
    }
};

2021年8月15日15:39:36：
很简单的二分：
注意mid*mid可能会越界，所以写成除的形式。

class Solution {
    public int mySqrt(int x) {
        if(x==0||x==1) return x;
        int l=0,r=x; //注意这个题目的左边界是从0开始的
        while(l<r){
            int mid=l+(r-l+1)/2;  //这样写可以防止l+r+1溢出
            if(mid<=x/mid) l=mid;   //注意写成if(mid<=x/mid),这样可以防止溢出的情况，
            else r=mid-1;
        }
        return l;
    }
}

74. 搜索二维矩阵

题目

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。 每行的第一个整数大于前一行的最后一个整数。

示例 1：

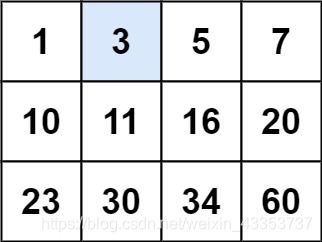
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

这个题目首先将二维矩阵转化为一维数组，第一个数下标为0，最后一个数下标为nm-1;

代码：

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& nums, int target) {
        if(!nums.size()||!nums[0].size())  return false;

        int m=nums.size(),n=nums[0].size();//m为行数，n为列数

        int l=0,r=n*m-1;
        while(l<r){
            int mid=(l+r)>>1;
            if(nums[mid/n][mid%n]>=target) r=mid;  //记住：坐标值/列数n=i,坐标%列数n=j;
            else l=mid+1;
        }   
        if(nums[l/n][l%n]==target) return true; //如果存在目标值，返回true;
        else return false;//如果不存在目标值，返回false;
    }
};

2021年8月15日16:23:09：

//本题考察的是二分法和坐标变换，注意用到的是列数，行数没什么用
//如果是一维的，显然直接使用二分法就可以求出来，这个题目虽然给的是二维矩阵，但是该矩阵:每行递增并且每行第一个数大于上一行最后一个数
//所以如果我们把这个矩阵展开成一个一维数组的话，就是一个递增的数组，即把矩阵的中每一个数映射成下标从0到m*n-1的一个一维递增数组，
//这个题目的难点就是怎么把一维下标对应到二维矩阵的横纵坐标，比如其下标为t，则其横坐标就是t/n,其纵坐标是t%n,跟m没关系，即跟列数有关系，跟行数没关系
//比如样例1中的10，其横坐标是4/4=1,纵坐标是4%4=0,因为10对应到一维数组其下标是4，再比如样例2中的23，其对应到一维数组下标是8,且n=4,横坐标是8/4=2,纵坐标是8%4=0
//这个题目我们对mid进行判断，matrix[mid/m][mid%m]和target的大小关系，即变成了一维数组的情况，很巧妙，y总牛皮！！！这种二维映射到一维的方法很常用。
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if(matrix.length==0||matrix[0].length==0) return false; //判空数组的情况
        int m=matrix.length,n=matrix[0].length; //否则求出行数和列数
        //下面就可以开始二分，先求出二分的边界
        int l=0,r=m*n-1; //求出二分的边界，由于二分只能对一维数组进行，所以这里要求的是一维的下标范围
        while(l<r){
            int mid=(l+r)>>1;
            if(matrix[mid/n][mid%n]>=target) r=mid; //判断一下如果中间数大于target,我们就更新r=mid
            else l=mid+1;
        }
        //最后二分出来的数可能大于target，所以最后我们还需要判断一下是否答案和目标值相同
        return matrix[r/n][r%n]==target;  //最后只需要判断一下matrix[r/n][r%n]和target是否相同，相同即存在target,否则不存在
    }
}

81. 搜索旋转排序数组 II

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,0,1,2,2,5,6] 可能变为 [2,5,6,0,0,1,2] )。

编写一个函数来判断给定的目标值是否存在于数组中。若存在返回 true，否则返回 false。

示例 1:

输入: nums = [2,5,6,0,0,1,2], target = 0
输出: true

示例 2:

输入: nums = [2,5,6,0,0,1,2], target = 3
输出: false

进阶:

这是 搜索旋转排序数组 的延伸题目，本题中的 nums 可能包含重复元素。 这会影响到程序的时间复杂度吗？会有怎样的影响，为什么？

二分代码：

class Solution {
public:
    bool search(vector<int>& nums, int target) {
        //多了就去掉，少了就补上
        if(nums.empty()) return false;  //如果为空，则一定不存在target，就返回false；
        int R=nums.size()-1;     //R代表最后一个元素的下标
        while(R>=0&&nums[R]==nums[0])  R--;  //把和开始元素相同的后面的元素删掉。如果整个数组全为nums[0],则数组中元素全部被删掉，则R=-1;注意这里是while循环，不是if。！！！
        if(R<0) return nums[0]==target;   //最后如果R<0,则说明数组中元素全为nums[0],所以我们只需要看一下nums[0]是否等于target，如果相等则返回true，如果不相等则返回false。

        //上面的代码执行完，则说明我们已经将数组最后等于nums[0]的元素全部删除。
        //下面就和之前那个题目一样的步骤了
        int l=0,r=R;
        while(l<r){
            int mid=(l+r+1)>>1;
            if(nums[mid]>=nums[0])l=mid;
            else r=mid-1;
        }
        if(target>=nums[0])r=l, l=0;
        else l++,r=R;
        while(l<r){
            int mid=(l+r)>>1;
            if(nums[mid]>=target)r=mid;
            else l=mid+1;
        }
        return nums[r]==target;
    }
};

这一句：while(R>=0&&nums[R]==nums[0]) R--;找到最小值最差情况下即数组元素全部相同的情况下需要O(n)的时间，因此最坏情况下复杂度为O(n)。所以我们也可以直接遍历这个数组，找到target即可：
直接遍历代码：

class Solution {
public:
    bool search(vector<int>& nums, int target) {
        for(int i=0;i<nums.size();i++){
            if(nums[i]==target){
                return true;
                break;
            }
        }
        return false;
    }
};

2021年8月15日17:13:17：

//首先先明白一点:非降序排列,指的是:ai<=ai+1,注意1,2,3,1,2这个不叫做非降序排列，因为出现了3,1这个降序。可以这样理解:可能有相同元素的升序数组
//这个题目和33题搜索旋转排序数组I很像，但是这个题目中有重复元素，当在相同元素处进行的旋转，那分开的两部分就不满足一部分>=nums[0],一部分严格
//我们可以象征性“删除”后一部分的那个相同元素，之所以是说象征性删除，是因为并不是真正的删除，而是移动的下标
//当我们删除掉后面相同的元素，我们就可以使用二分的方法类似于33的做法，使用两次二分求出是否存在target
class Solution {
    public boolean search(int[] nums, int target) {
        if(nums.length==0) return false;  //判空
        int n=nums.length;
        int R=n-1;  //R是数组最右边数的下标，我们现在要开始删除和nums[0]相同的后面的数了
        while(R>=0&&nums[R]==nums[0]) R--;  //注意一定要写上R>=0这个条件，避免出现下标越界的异常，象征性删除数组后面的元素
        if(R<0) return nums[0]==target; //如果数组中的数字都相同，即R<0,我们只需要判断一下是否target和这个数相同
        //否则我们就删除掉了后半部分和nums[0]相同的部分
        int l=0,r=R;  //二分的左右边界，注意右边界是R，不是R-1
        while(l<r){
            int mid=(l+r+1)>>1;
            if(nums[mid]>=nums[0]) l=mid;
            else  r=mid-1;
        }
        //这样就找到了前后两部分的分界点，下面我们重新确定左右边界，并用于查找target
        if(target>=nums[0]) l=0;
        else{
            l=r+1;
            r=R;  //注意这里是R,不是n-1
        }
        while(l<r){
            int mid=(l+r)>>1;
            if(nums[mid]>=target) r=mid;
            else l=mid+1;
        }
        return nums[r]==target; //最后看一下target是否和nums[r]相同
    }
}

153. 寻找旋转排序数组中的最小值

假设按照升序排序的数组在预先未知的某个点上进行了旋转。例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2]。

请找出其中最小的元素。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
示例 3：

输入：nums = [1]
输出：1

代码：

class Solution {
public:
    int findMin(vector<int>& nums) {
        int l=0,r=nums.size()-1;   //确定二分的左右边界。
        while(l<r){
            int mid=(l+r)>>1;
            if(nums[mid]<=nums.back()) r=mid;  // 看图,
            else l=mid+1;
        }
        return nums[r];
    }
};

2021年8月15日17:36:21：

2021年8月15日17:46:16：

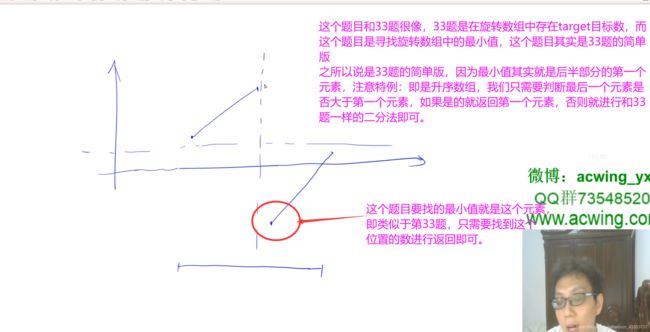
//这个题目和33题很像，33题是在旋转数组中存在target目标数，而这个题目是寻找旋转数组中的最小值，这个题目其实是33题的简单版
//之所以说是33题的简单版，因为最小值其实就是后半部分的第一个元素，注意特例：即是升序数组，我们只需要判断最后一个元素是否大于第一个元素，如果是的就返回第一个元素
//注意数组中的所有数均不相同，
class Solution {
    public int findMin(int[] nums) {
        int n=nums.length;
        if(n==1) return nums[0];
        //否则就进行二分
        int l=0,r=n-1;
        if(nums[r]>nums[l]) return nums[0]; //如果nums[r]>nums[l],因为数组中的数是均不相同的，所以这样就是说数组是升序的，所以我们返回第一个数nums[0]
        while(l<r){
            int mid=(l+r)>>1;
            if(nums[mid]<nums[0]) r=mid;  //因为数组中的数均不相同，所以这里可以不用写=，为了找到后半部分的第一个位置，所以我们需要往左边去，即更新r=mid
            else l=mid+1;
        }
        return nums[r]; //返回nums[r]
    }
}

154. 寻找旋转排序数组中的最小值 II

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

请找出其中最小的元素。

注意数组中可能存在重复的元素。

示例 1：

输入: [1,3,5]
输出: 1

示例 2：

输入: [2,2,2,0,1]
输出: 0

说明：

这道题是 寻找旋转排序数组中的最小值 的延伸题目。 允许重复会影响算法的时间复杂度吗？会如何影响，为什么？

这个题目类似于81题，虽然可以使用二分，但是如果全部元素均相同，则此时为最坏情况，时间复杂度为0（n）;
代码：

class Solution {
public:
    int findMin(vector<int>& nums) {
        if(nums.empty()) return false;    	//这个题目整体思路类似于81题。如果数组为空，则一定不存在最小的元素，返回false；
        if(nums.size()==1) return nums[0];	//如果数组长度为1，则最小的元素一定是nums[0]。
        int R=nums.size()-1;	//把后面的重复元素删掉，否则下面无法使用二分法。
        while(R>=0&&nums[R]==nums[0]) R--;
        if(R<0) return nums[0];

        int l=0,r=R;
        while(l<r){
            int mid=(l+r)>>1;
            if(nums[mid]<=nums[R])r=mid;
            else l=mid+1;
        }
        return nums[r];
    }
};

方法二：

class Solution {
public:
    int findMin(vector<int>& nums) {
        int l=0,r=nums.size()-1;    //方法二,左右端点
        while(l<r&&nums[r]==nums[0]) r--;   //把数组后面等于nums[0]的元素全部删掉，
        if(nums[l]<=nums[r]) return nums[0];    //将后半段等于nums[0]的元素全部删除之后，如果nums[l]<=nums[r]，说明剩余元素是递增的，最小元素一定是nums[0]或者说是nums[l]。

        //不满足第6句代码，说明后半段在删除完等于nums[0]的元素之后还剩余元素。
        while(l<r){
            int mid=(l+r)>>1;
            if(nums[mid]<nums[0])r=mid; //注意这里if条件里面要么写nums[mid]=nums[0])，或者写nums[mid]>=nums[0]。
            else l=mid+1;
        }
        return  nums[r];
    }
};

2021年8月15日18:13:32：

//这个题目和前面的题目基本上还是差不多，但是边界条件特别多，需要仔细考虑，首先如果只有一段，我们就可以不用做了，直接返回
class Solution {
    public int findMin(int[] nums) {
        int n=nums.length;
        if(n==1) return nums[0];
        if(nums[n-1]>nums[0]) return nums[0];   //这个特判可以不用写
        int R=n-1;
        while(R>=0&&nums[R]==nums[0]) R--;
        if(R<0) return nums[0];
        //只有一段，直接返回nums[0]
        if(nums[R]>nums[0]) return nums[0]; //这个特判不要忘了写
        int l=0,r=R;
        while(l<r){
            int mid=(l+r)>>1;
            if(nums[mid]<nums[0]) r=mid;
            else l=mid+1;
        }
        return nums[r];
    }
}

162. 寻找峰值

题目

峰值元素是指其值大于左右相邻值的元素。

给你一个输入数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

假设 nums[-1] = nums[n] = -∞ 。

注意：

1 <= nums.length <= 1000
-231 <= nums[i] <= 231 - 1
对于所有有效的 i 都有 nums[i] != nums[i + 1]

示例 1：

输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。
示例 2：

输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5 
解释：你的函数可以返回索引 1，其峰值元素为 2；
     或者返回索引 5， 其峰值元素为 6。

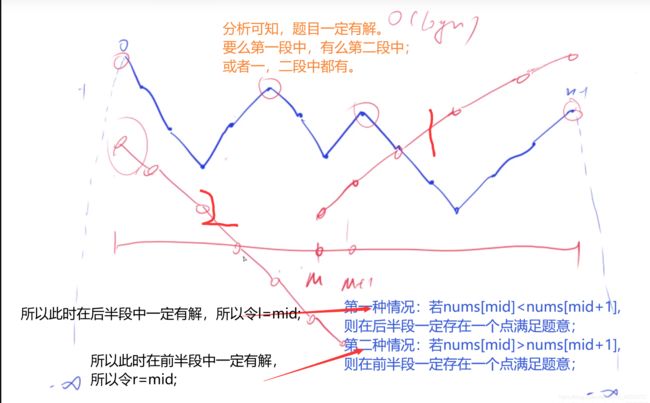
这道题目虽然不具有明显的二段性，但仍可以使用二分法。

题目保证一定有解。

代码：

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int l=0,r=nums.size()-1;   //确定左右边界。
        while(l<r){
            int mid=(l+r)>>1;     
            if(nums[mid]>nums[mid+1]) r=mid;   //如果nums[mid]>nums[mid+1]，则在前半段中；
            else l=mid+1;  //否则，在后半段中。
        }
        return r;    //找到了，返回下标。
    }
};

注意：nums[mid]>nums[mid+1]这一段代码，
不需要判断mid+1是否会出界，因为，若mid+1出界，
则mid=n-1,且l=r=n-1,此时l和r相同，跳出while循环，所以不需要特判。

2021年8月15日18:43:22：

//这个题目虽然不是有序的但是也可以使用二分法，题目中的任意两个相邻数都不相同，我们可以取中点，看一下中点a和中点下一个数b的大小关系，注意左右两边都是负无穷
//如果a
//同理，如果a>b,z则往左看，第一次出现下降的位置就是峰值，否则左边界点就是峰值，通过上面的分析，数组中一定存在峰值，
//并且如果ab,我们就在左边找，所以无论是哪种情况，区间都可以缩小一半，
class Solution {
    public int findPeakElement(int[] nums) {
        int n=nums.length;
        if(n==1) return 0;  //如果数组中只有一个元素，由于左右边界均是负无穷，所以峰值下标就是0,注意这个题目要返回的是下标，不是值。
        //下面使用二分法
        int l=0,r=n-1;
        while(l<r){
            int mid=(l+r)>>1;
            if(nums[mid]>nums[mid+1]) r=mid;  //如果a>b,就往左边找，注意这里nums[mid+1]不会越界，因为如果nums[mid+1]越界，就意味着mid取到了n-1,
            //而如果mid取到了n-1,由于我们是下取整，就意味着此时l和r都取到了n-1,而如果l和r都取到了n-1,是不会进入到while循环的，所以不会越界
            else l=mid+1;
        }
        //一旦结束循环，就意味着l和r相同，而两者之所以会相同，是因为l往左或者r往右，即出现了转折点，即峰值
        return r; /r或者l就是答案,注意题目要求的是下标，不是值，所以不要写nums[r],而应该直接写r或者l
    }
}

//这个题目的二分法用的十分巧妙，如果不执行了if条件，即一直执行的是else，则峰值就是右边界，如果一直执行的是if,峰值就是左边界，而如果两个语句都指向了就说明中间有转折点，即峰值，而l和r会在峰值点碰面。

240. 搜索二维矩阵 II （从右上角元素开始考虑，每次去掉一行或者一列）

(这个题目方法严格来说不算二分法，但是有一点相似）

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例 1：

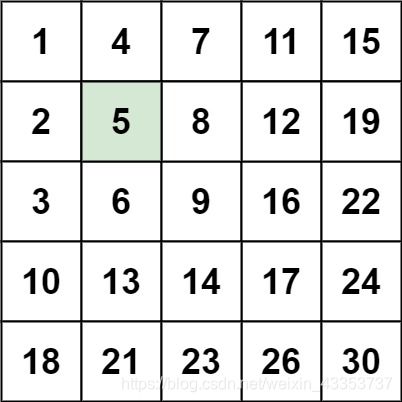
输入：matrix = [
[1,4,7,11,15],
[2,5,8,12,19],
[3,6,9,16,22],
[10,13,14,17,24],
[18,21,23,26,30]
], 
target = 5

输出：true

提示：

m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-109 <= matix[i][j] <= 109
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-109 <= target <= 109

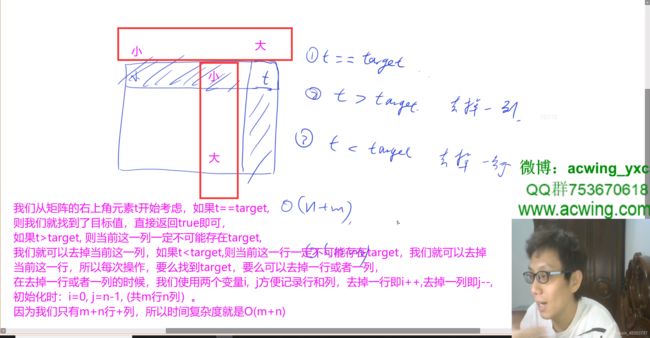
//暴力解法：直接遍历整个矩阵，时间复杂度为O(n*m),即两层for循环即可;

//方法二：从右上角元素值t开始枚举，如果t==target,则找到目标值，结束并返回即可；如果t>target,则说明t所在列均不可能有值为target，因为矩阵从左到右递增，从上到下也递增，所以我们此时可以去掉t所在这一列；如果t

代码：

class Solution {
public:     
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        if(matrix.size()==0||matrix[0].size()==0) return false;   //如果行为空（matrix.size()）或者列为空（matrix[0].size()），则一定不存在目标值，返回false。
        int n=matrix.size(),m=matrix[0].size(); //否则用n记录总行数，m记录总列数。
        int i=0,j=m-1;  //i记录行数，j记录列数，即初始化时在右上角。
        while(i<n&&j>=0){   //只要i,j不出界，i最大为n-1，j最小为0；
            int t=matrix[i][j];   //用t记录当前值。
            if(t==target) return true;  //如果t==target，即找到了target，返回true即可。
            else if(t>target) j--;  //如果t>target,则去掉当前列；
            else i++;   //如果t
            //while一直在循环，如果最后能找到target，则一定在第9句返回true。如果当while循环完还没有结束程序，即我们把整个矩阵全部删除完毕了（即j=-1或者i=n了，while循环条件就不满足了），还没有找到目标值，说明矩阵中不存在target，while语句之后返回false。
        }
        return false;
    }
};

2021年8月15日20:47:37：

//这个矩阵的性质是：每行的元素从左到右升序排列。每列的元素从上到下升序排列。即这个矩阵和I不同的是:只具有每行和每列的单调性，没有全局单调性，而I有全局单调性
//
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        if(matrix.length==0||matrix[0].length==0) return false;
        int m=matrix.length,n=matrix[0].length; //求出数组的行数和列数
        int i=0,j=n-1;  //初始化时，i在第一行，j在最后一列
        while(i<m&&j>=0){  //行数最大为m-1,j最小为0，注意不能出界
            int t=matrix[i][j]; //这个数多次用到，我们用t记录
            if(t==target) return true;  //找到了target，直接返回true
            else if(t>target) j--;  //如果t比target要大，则当前这一列的所有数都比target大，所以去掉当前列
            else i++; //否则去掉当前这一行，即i++
        }
        return false; //最后如果上面的while循环没有返回值，就说明矩阵中不存在target，返回false
    }
}

274. H 指数 (排序）

给定一位研究者论文被引用次数的数组（被引用次数是非负整数）。编写一个方法，计算出研究者的 h 指数。

h 指数的定义：h 代表“高引用次数”（high citations），一名科研人员的 h 指数是指他（她）的 （N 篇论文中）总共有 h 篇论文分别被引用了至少 h 次。且其余的 N - h 篇论文每篇被引用次数 不超过 h 次。

例如：某人的 h 指数是 20，这表示他已发表的论文中，每篇被引用了至少 20 次的论文总共有 20 篇。

 示例：

输入：citations = [3,0,6,1,5]
输出：3 
解释：给定数组表示研究者总共有 5 篇论文，每篇论文相应的被引用了 3, 0, 6, 1, 5 次。
     由于研究者有 3 篇论文每篇 至少 被引用了 3 次，其余两篇论文每篇被引用 不多于 3 次，所以她的 h 指数是 3。

提示：如果 h 有多种可能的值，h 指数是其中最大的那个。

算法分析：

代码：

class Solution {
public:
    int hIndex(vector<int>& c) {
        sort(c.begin(),c.end(),greater<int>()); //先将数组从大到小排序
        int n=c.size(); //求出数组长度n
         // 由定义可知 h 指数最大是 c.size();
        // 6, 5, 3, 1, 0; 我们从最后一个数往前推， 若 c[h - 1] >= h, 那么直接返回 h, 因为c[h - 1] 是 [0, h - 1] 中最小的数 
        for(int h=n;h>0;h--){  //从n开始枚举h(因为n篇论文所以最大为n),最小为1，每次将一，注意h有可能不是数组中的数，因为h是篇数，而a[h]是引用次数
            if(c[h-1]>=h){  //如果满足c[h-1]>=h，即是满足前h个数>=h,比如样例中(6,5,3,1,0)h=5的时候，c[5-1]=0,很显然不满足要求
                return h;
            }
        }
        return 0;   //最后如果连一都没有返回，说明都不行，我们就返回0
    }
};

java代码：

class Solution {
    public int hIndex(int[] c) {
        Arrays.sort(c);
        int n=c.length;
        for(int h =n;h>=1;h--){
            if( c[n-h] >=h) return h;
        }
        return 0;
    }
}

java分析：
由于java实现数组倒序排列比较麻烦，所以这里我们转换思路。

排序

• 1、从小到大排序
• 2、从前往后枚举，找到最小c[i]满足n - i即可，即满足[i,n - 1]中的n - i个数使得每个对应的引用次数都比n - i高

代码：

class Solution {
    public int hIndex(int[] c) {
        Arrays.sort(c);
        int n = c.length;
        for(int i = 0;i < n;i ++)
        {
            if(c[i] >= n - i)
            {
                return n - i;
            }
        }
        return 0;
    }
}

题目说到，h指数是：h 篇论文分别被引用了至少 h 次。通过排序后，若存在着在[i, n - 1]区间的n - i篇论文，且每一篇论文引用的次数至少是n - i次，即等价于在区间中引用次数最少的一定满足 被引用次数 >= n - i次，即c[i] >= n - i。在所有存在的情况下，找到最小的i，则引用次数即n-i一定最大。

2021年8月15日21:26:02：

//h最大为数组长度n,我们自己求h指数的时候，是从最大的数开始依次减小枚举的，比如:[3,0,6,1,5],我们先看是否有6篇文章>=6,没得，再看是否有5篇文章>=5,没得，
//再看是否有3篇文章>=3,发现有，所以h=3.转为算法:我们将数组从大到小排序，然后从大到小枚举数组中的每一个数，且h最大为n
//每次看一次当前是否有h个数>=h,判断是否有h个数>=h,其实就是判断最大的h个数是否>=h,因为有h个数>=h,一定是最大的h个数>=h,
//所以我们只需要判断一下前h个数是否都>=h即可，而数组是从大到小排好序的，所以我们只需要判断第h个数Ch是否>=h即可,这样我们就可以找到一个最大的h，
//如果最后也没有找到满足条件的h,h就是0，最后返回0,并且注意第h个数下标是h-1,而java中没有倒序排序的功能，
//我们可以转换思路，先从小到大对数组排序，从大到小枚举h,即从n到1枚举，然后每次判断C[n-h]是否>=h即可
class Solution {
    public int hIndex(int[] c) {
        Arrays.sort(c); //注意先判断
        for(int h=n;h>=1;i--){  //h从从大到小枚举
            if(c[n-h]>=h){  //之所以是c[n-h]可以举例，例如当h=n是c[n-h]=c[0],即需要看最小的一篇文章的引用次数是否满足要求，显然是正确的。
                return h; //找到了h就及时输出返回。
            }
        }
        return 0; //最后如果没有找到h的话，就返回0
    }
}

2021年11月9日11:08:15：

class Solution {

//我们先将数组从大到小排序,从大到小枚举h,看当前是不是有h个数>=h, 因为我们要看的是当前是不是有h个数>=h,其实就是要看最大的h个数是不是>=h就可以了
//因为如果有h个数>=h的话，一定就是最大的h个数>=h,所以我们只需要看前h个数是不是都>=h即可，由于我们已经将数组从大到小排好序了，
//所以我们只需要看第h个数这个数是不是>=h就可以了(因为第h个数是前h个数中最小的数，如果这个数都>=h的话，则前h个数一定都>=h),即看a[h]是不是>=h即可
//我们从大到小找到最大的h即可，如果找不到就是0，注意java中只能从小到大排序
//并且注意第h个数下标是h-1,而java中没有倒序排序的功能，
//我们可以转换思路，先从小到大对数组排序，从大到小枚举h,即从n到1枚举，然后每次判断C[n-h]是否>=h即可

    public int hIndex(int[] cs) {
        int n=cs.length;
        Arrays.sort(cs);  //将数组从小到大排序
        for(int h=n;h>=1;h--){  //从大到小枚举引用次数h,注意h最小是1，所以最后是h>0,而不是>=0,或者写h>=1,
            if(cs[n-h]>=h) return h; //这里之所以是c[n-h]可以举例，例如当h=n是c[n-h]=c[0],即需要看最小的一篇文章的引用次数是否满足要求，显然是正确的。
            //一定要注意这里不是cs[n-h-1],就是cs[n-h],可以再举一个例子，当h=1的时候，显然就需要看cs[n-1]，即最后一篇文章，最后返回的是次数h
        }
        return 0;  
    }
}

275. H 指数 II

题目

给定一位研究者论文被引用次数的数组（被引用次数是非负整数），数组已经按照 升序排列 。编写一个方法，计算出研究者的 h 指数。

h 指数的定义: “h 代表“高引用次数”（high citations），一名科研人员的 h 指数是指他（她）的 （N 篇论文中）总共有 h 篇论文分别被引用了至少 h 次。（其余的 N - h 篇论文每篇被引用次数不多于 h 次。）"

示例:

输入: citations = [0,1,3,5,6]
输出: 3 
解释: 给定数组表示研究者总共有 5 篇论文，每篇论文相应的被引用了 0, 1, 3, 5, 6 次。
     由于研究者有 3 篇论文每篇至少被引用了 3 次，其余两篇论文每篇被引用不多于 3 次，所以她的 h 指数是 3。
 

说明:

如果 h 有多有种可能的值 ，h 指数是其中最大的那个。

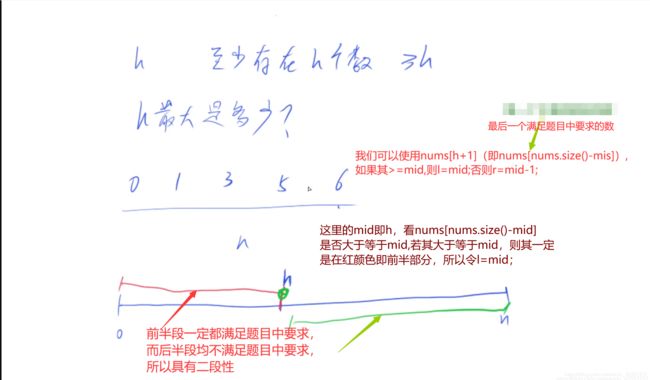
首先确定h的范围，h最大为n,最小为0；

本题具有二段性，即是否具有x个数，使得至少存在x个数>=x,一定是最后h个数>=h,所以我们需要看一下最后倒数h个数中最小的那个数是否满足>=h就可以了，记住最后倒数h个数中最小的那个数下标为nums.size()-mid;前一段满足这个性质，而后一段不满足这个性质，
所以可以使用二分法；

代码：

//我们知道
class Solution {
public:
    int hIndex(vector<int>& nums) {
        int l=0,r=nums.size();   //确定边界，h最小为0，最大为nums.size();

        while(l<r){
            int mid=(l+r+1)>>1;  
            if(nums[nums.size()-mid]>=mid) l=mid;  //看图，和上面的说明，如果倒数h个数中最小的数大于h,则可能有更大的h，所以我们将l更新为mid,最后当l和r重合的时候，r就是所求的最大h,
            else r=mid-1;
        }
        return l;  //注意返回的是l或者r;h不一定是在数组中；
    }
};

2021年8月16日10:17:06：

//这个题目和上个题目的不同就是这个题目是排好序的，所以我们就不需要再对数组进行排序了，我们直接直接使用这个题目的方法做，时间复杂度是O(n)
//但是我们还可以使用二分法来优化解决，
class Solution {
    public int hIndex(int[] c) {
        int n=c.length;
        //下面进行二分
        //特别注意，右边界最大为n，不是n-1,这里不是下标，而是最大引用次数，h指数最大为n，一定一定一定要注意。
        int l=0,r=n;  //二分的左右边界，注意右边界最大为n，左边界为最小是0。
        while(l<r){
            int h=(l+r+1)>>1;
            if(c[n-h]>=h) l=h;  //当满足c[n-h]的时候，我们的h还可以更大一点，所以更新l=h
            //这里c[n - h] 是不会越界的，因为当h=0的时候,l和r一定是相等的，就跳出while循环了
            else r=h-1;
        }
        return r;   //最后l和r都走到最大的h处，
    }
}

2021年11月9日11:07:52：

class Solution {

//这个题目已经从小到大排好序了,所以我们就没有必要再使用O(nlogn)的排序了,我们可以直接使用上一题的循环扫描一遍,但是时间是O(n)的,我们考虑优化
//我们考虑是否有二段性,如果有的话,我们就可以使用二分了,假设数组是从大到小排好序的,并且h是最大的一个满足a[h]>=h的数,即这个引用指数就是h
//那么如果h更大一些是否可以呐？显然是不可以的,因为我们已经说了h是最大的满足a[h]>=h的数,也就是说所有大于h的数都不满足这个性质
//而所有小于h的数都满足a[h]>=h,所以具有二段性,我们就可以使用二分优化,时间就是O(logn)

    public int hIndex(int[] cs) {
        int n=cs.length;
        //数组已经从小到大排好序了,所以我们无需再排序了
        int l=0,r=n;  //二分的左右边界,最小是0,最大是数组的长度n
        while(l<r){
            int mid=(l+r+1)>>1;
            if(cs[n-mid]>=mid) l=mid;  //check函数的确定:看是否满足要求,即看cs[x]是否>=h,如果满足>=mid,说明我们的答案应该是>=mid的,我们就更新l=mid,即让数更大一些
            //cs[x]中坐标x的确定方法：x应该是从大到小数第mid个数,而n-1是从大到小数第1个数,n-2是从大到小数第2个数,所以第mid个数的下标是n-mid
            else r=mid-1;
        }
        //注意上面cs[n-mid]是一定不会越界的，因为当mid=0的时候，l和r一定是相等的，就跳出while循环了
        return r; //最后返回mid，即r
    }
}

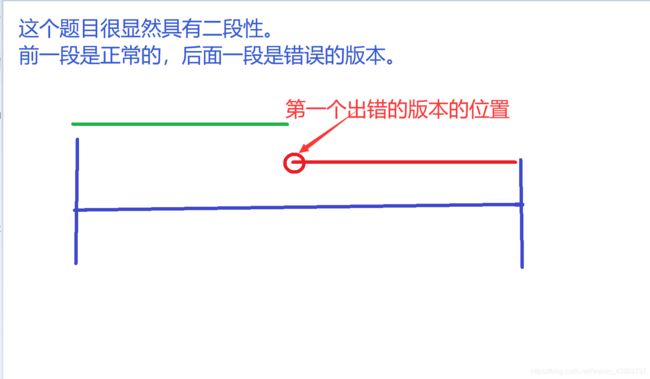
278. 第一个错误的版本

题目

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, …, n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version
是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例:

给定 n = 5，并且 version = 4 是第一个错误的版本。

调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true

所以，4 是第一个错误的版本。 

代码：

// The API isBadVersion is defined for you.
// bool isBadVersion(int version);

class Solution {
public:
    int firstBadVersion(int n) {
        int l=1,r=n;    //先确定左右断点，注意这一题目中l=1，不是0.   r=n,不是n-1;
        while(l<r){
            int mid=((long long)l+r)>>1;   注意r可能溢出，所以需要转为long long;
            if(isBadVersion(mid)) r=mid;    //即如果isBadVersion(mid)返回ture,则第一个出错的版本一定在mid的左边或者mid本身。
            else l=mid+1;
        }

        return l;    //找到第一个出错的版本，并返回。

    }
};

2021年8月16日10:43:293：

/* The isBadVersion API is defined in the parent class VersionControl.
      boolean isBadVersion(int version); */
//这个题目是一个很简单的二分法，但是要注意的是题目中的isBadVersion(mid)这个函数，是错误版本返回true,而是正确版本返回false,别自以为是，看一下样例中的例子
public class Solution extends VersionControl {
    public int firstBadVersion(int n) {
        int l=1,r=n;
        while(l<r){
            int mid=(l+r)>>1;
            if(isBadVersion(mid)==true) r=mid;  //注意这里的isBadVersion(mid)这个函数，是错误版本返回true,不要搞混了。
            else l=mid+1;
        }
        return r;
    }
}

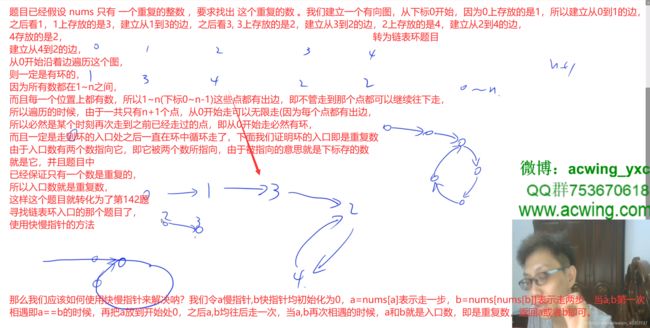
287. 寻找重复数

题目

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，找出 这个重复的数 。

示例 1：

输入：nums = [1,3,4,2,2]
输出：2
示例 2：

输入：nums = [3,1,3,4,2]
输出：3
示例 3：

输入：nums = [1,1]
输出：1
示例 4：

输入：nums = [1,1,2]
输出：1
 

提示：

2 <= n <= 3 * 104
nums.length == n + 1
1 <= nums[i] <= n
nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现 一次

抽屉原理：有N个抽屉和N+1个苹果，则一定至少有两个苹果在一个抽屉里。

我们使用1——n代表抽屉个数，即yl或者yr代表的是左/右抽屉个数，而我们枚举的cnt代表的是数组中落到l——m之间的个数，即苹果个数，注意和上面几道题目的区别。

代码：

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int n=nums.size()-1;   //1——n代表抽屉个数,抽屉个数等于苹果个数-1，所以r=n=总数-1；

        int l=1,r=n;   //l————r是记录数值的。
        while(l<r){
            int mid=(l+r)>>1;
            int cnt=0;    //cnt用于遍历在l————mid之间的苹果个数；cnt用于统计左半边数的个数。
            for(auto x:nums){    //遍历nums数组中的所有元素x
                if(x>=l&&x<=mid) cnt++;  //如果x在l和mid之间则苹果个数加1；
            }

            if(cnt>mid-l+1) r=mid;  //看图，若苹果个数>左边抽屉个数，则重复元素在左边，所以令r=mid;
            else l=mid+1;   //否则，令l=mid+1;
        }
         return l;    //注意返回的是l（l记录的是数值），不是nums[l];
    }
};

2021年8月16日10:53:55：

非二分法：

转为142题寻找链表环的入口那个题目：

//因为数组中的数字都在1到n之间，而这个数组中包含了n+1个整数，所以一定至少存在一个重复的整数，即是抽屉原理，而且题目假设nums只有一个重复的整数,现在让我们找出这个重复的数。
//这个题目的要求很苛刻，不能修改数组，使用O(n)空间，O(1)时间，看图，可以转为142题寻找链表环入口那个题目
class Solution {
    public int findDuplicate(int[] nums) {
        int a=0,b=0;  //a是慢指针每次走一步，b是快指针每次走两步
        while(true){  //这里直到找到入口元素，即重复数再停止，所以是while(true)
            a=nums[a];  //a每次走一步
            b=nums[nums[b]];  //b每次走两步
            if(a==b){  //一直到a和b相遇，我们就把a重新放到开头，之后让a,b每次走一步。再次相遇
                a=0;  //将a再次放到开始位置
                while(a!=b){
                    a=nums[a];
                    b=nums[b];
                }
                //注意while(true)语句内一定要写return语句，并且要写在if语句内
                return a;   //最后while(a!=b)结束的条件就是a和b相遇，即a==b,此时a和b相遇在重复数了，注意返回的不是nums[a]或者nums[b],而是a或者b
            }
        }
    }
}

时间复杂度：O(n)

解法二：二分法：
算法
(分治，抽屉原理) O(nlogn)
这道题目主要应用了抽屉原理和分治的思想。

可以解决重复的数不止一个的情况，

抽屉原理：n+1 个苹果放在 n 个抽屉里，那么至少有一个抽屉中会放两个苹果。

用在这个题目中就是，一共有 n+1 个数，每个数的取值范围是1到n，所以至少会有一个数出现两次。

然后我们采用分治的思想，将每个数的取值的区间[1, n]划分成[1, n/2]和[n/2+1, n]两个子区间，然后分别统计两个区间中数的个数。
注意这里的区间是指 数的取值范围，即是数值，非下标，而不是 数组下标。

划分之后，左右两个区间里一定至少存在一个区间，区间中数的个数大于区间长度。
这个可以用反证法来说明：如果两个区间中数的个数都小于等于区间长度，那么整个区间中数的个数就小于等于n，和有n+1个数矛盾。

因此我们可以把问题划归到左右两个子区间中的一个，而且由于区间中数的个数大于区间长度，根据抽屉原理，在这个子区间中一定存在某个数出现了两次。

依次类推，每次我们可以把区间长度缩小一半，直到区间长度为1时，我们就找到了答案。

复杂度分析
时间复杂度：每次会将区间长度缩小一半，一共会缩小 O(logn)次。每次统计两个子区间中的数时需要遍历整个数组，时间复杂度是 O(n)。所以总时间复杂度是 O(nlogn)。
空间复杂度：代码中没有用到额外的数组，所以额外的空间复杂度是 O(1)。

// 划分的区间：[l, mid], [mid + 1, r]

class Solution {
public:
    int duplicateInArray(vector<int>& nums) {
        int l = 1, r = nums.size() - 1;
        while (l < r) {
            int mid = l + r >> 1; // 划分的区间：[l, mid], [mid + 1, r]
            int s = 0;
            for (auto x : nums) {
            	if(x >= l && x <= mid){
            		s ++;
				}
			}
            
            if (s > mid - l + 1) r = mid;
            else l = mid + 1;
        }
        return r;
    }
};

2021年11月4日10:25:45：
转变为找环的入口那个题目：

class Solution {

//抽屉原理做时间是O(nlogn),可以把这个题目转化为求环的入口那个题目，即142题，首先需要把这个题目转为图论的问题，给数组中的所有数写上下标

    public int findDuplicate(int[] nums) {
        int n=nums.length;
        int f=0,s=0;  //快慢指针，对应的是下标，一开始都初始化为0
        while(true){
            f=nums[nums[f]]; //快指针每次往后走两步
            s=nums[s];  //慢指针每次往后走一步
            if(f==s){ //当两个指针相遇的时候，我们把慢指针放到开头
                f=0;
                while(f!=s){  //当两个指针没有相遇
                    f=nums[f]; //两个指针每次往后走一步
                    s=nums[s];
                }
                return f; //最后返回的是f,不是nums[f],因为环的入口就是f，如果是nums[f]的话就是环的入口的下一个元素了
            }
        }
    }
}

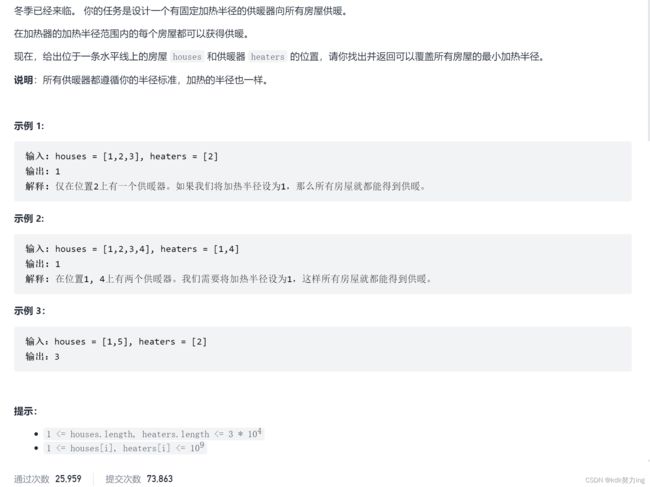
475. 供暖器

2021年12月20日09:49:31：

class Solution {

//首先最小半径是符合二分的性质的,假设x是最小的符合要求的,则>=x的都可以符合要求,而
//对于一个供暖期点,其都可以形成一个覆盖区间,对于所有的房间点,我们都需要找到最左边的一个区间使得这个区间的覆盖范围是包含这个房间的
//当房间从左往右移动的时候,每一个房间所对应的区间(即第一个可以覆盖房间的区间)也一定是往右的(可以使用反证法证明),所以这里我们就可以使用双指针算法了(即两个指针是具有单调性的)
//总的时间就是双指针扫描区间是O(n),而二分的时间是O(logN),(N是int的范围),所以总的时间就是O(n*logN)
//

    public int findRadius(int[] a, int[] b) { //数组a是所有的房间,数组b是所有的供暖器点
        Arrays.sort(a); //题目中没有说两个数组是有序的我们手动排个序
        Arrays.sort(b);
        long l=0,r=Integer.MAX_VALUE;  //二分的左右边界,l+r可能会爆int,所以这里用long, l,r是半径所有可能的取值点
        while(l<r){
            long mid=(l+r)/2;  
            if(check(mid,a,b)) r=mid;  //mid是成立的,所以答案应该比mid小,否则答案比mid大
            else l=mid+1;
        }
        return (int)r; //最后返回r即可
    }

    public boolean check(long mid,int[] a,int[] b){ //check函数判断的就是以mid为半径是否可以覆盖所有的房子
        int n=a.length,m=b.length;  
        for(int i=0,j=0;i<n;i++){ //i是遍历所有的房子,i,j是双指针来判断每一个房子是否可以被覆盖住,i是指向否则,j是能够覆盖这个房子的区间的下标，当i指针往后走的时候，j指针一定是单调往后走的，
//而在写代码的时候判断这个供暖期半径是否可以覆盖这个房子就是让b[j]-a[i](注意是绝对值),如果这个差值大于mid(mid就是半径)，说明这个区间无法完成覆盖，我们就应该让j++,即往右看是否下一个区间可以覆盖这个房子
//最后如果说j>=m了，说明对于当前房子a[i]来说，所有的供暖期都是覆盖不住的，我们就返回false, 否则如果所有的房间都能够覆盖住，我们就返回true
            while(j<m&&Math.abs(b[j]-a[i])>mid) j++;
            if(j>=m) return false;  //有一个房子覆盖不住就说明所有的区间都无法覆盖住当前房子，我们就返回false
        }
        return true;  //上面没有返回false，就说明所有的区间都能够被覆盖，我们就返回true
    }
}

540. 有序数组中的单一元素

2021年11月9日13:29:26：

class Solution {

//可以使用异或,但是时间复杂度是O(n)的,这里就没有用到数组有序这个条件,我们可以使用二分将时间复杂度降到O(logn)
//比如样例[-5,-5,0,0,1,1,2,3,3,4,4,8,8],因为数组是有序的,我们每两个相邻的数分为一组,则有[-5,-5],[0,0],[1,1],[2,3],[3,4],[4,8],[8,9](最后补上一个不同的数)
//我们可以发现这里的二段性：在只有一个数之前的那些数组内的数都是相同的是,而从答案那个数开始组内的两个数都是不同的,答案就是分界点右边的第一个数
//我们这里二分的是不同的组号

    public int singleNonDuplicate(int[] nums) {
        int n=nums.length;
        int[] a=new int[n+1];
        for(int i=0;i<n;i++) a[i]=nums[i];
        a[n]=nums[n-1]+1; //我们需要在数组的最后补上一个数，就补上最后一个数加一就行了
        int l=0,r=(n+1)/2-1;  //组号从0开始，最后一组是(n+1)/2,注意还要减一，所以我们的下标是从0开始的，而这里指的是个数
        while(l<r){
            int mid=(l+r)>>1;
            if(a[mid*2]!=a[mid*2+1]) r=mid; //mid*2是这一组的第一个数，mid*2+1是这一组的第二个数，
            else l=mid+1;
        }
        //最后l和r就走到了边界区间
        return a[r*2]; //最后的答案是这一组的第一个数，即a[r*2]
    }
}

2021年11月9日13:39:42：

注意上面的做法的时间还是O(n),因为我们遍历了原数组
下面的时间才是O(logn)的
class Solution {
    public int singleNonDuplicate(int[] nums) {
        int n=nums.length;
        int l=0,r=n-1;
        while(l<r){
            int mid=(l+r)>>1;
            //如果mid为偶数,mid^1为mid+1
            //如果mid为奇数,mid^1为mid-1
            if(nums[mid]!=nums[mid^1]) r=mid;
            else l=mid+1;
        }
        return nums[r];
        
    }
}

补充题字节：给定数组，每个元素代表一个木头的长度，木头可以任意截断， 从这堆木头中截出至少k个相同长度为m的木块，已知k，求max(m)

题目描述

给定长度为n的数组，每个元素代表一个木头的长度，木头可以任意截断，从这堆木头中截出至少k个相同长度为m的木块。已知k，求max(m)。

输入两行，第一行n, k，第二行为数组序列。输出最大值。

输入
5 5
4 7 2 10 5
输出
4

解释：如图，最多可以把它分成5段长度为4的木头

ps:数据保证有解，即结果至少是1。

题目分析
方法一：暴力。大概思路就是从1遍历到木棍最长的长度，每次遍历的长度作为m，如果可以将所有木头截出来k个长度为m的木块，则更新最大值，最后输出最大值即可。可以通过下面的伪代码片段辅助理解：

 public static void main(String[] args) {
        int n=in.nextInt(),k=in.nextInt();
        int[] a=new int[n];
        int maxP=0; //maxP是所有可能截到的最大值，即a数组中的单个元素的最大值
        for(int i=0;i<n;i++) {
            a[i]=in.nextInt();
            maxP=Math.max(maxP,a[i]);
        }
        int res=0;  //res是答案
        for(int m=1;m<=maxP;m++){ //m是所有可能截取的范围，从1到maxP
            int cnt=0; //cnt记录以i为长度可以截取出的根子的数量
            for(int x:a) cnt+=x/m;  //遍历数组a,cnt是当前棍子可以截取到的长度为m的棍子的数量
            if(cnt>=k) res=Math.max(res,m); //如果当前可以截取出来的超过k段，我们就更新结果
            //注意题目要求我们求的是最大的m,所以我们用m更新res
            //即要截取出来至少k个长度为m的根子
        }
        System.out.println(res);
    }

上面的代码也比较容易理解，这里就不多展开说了。时间复杂度也很容易看出来是O(n * len), len为木头中最大的长度。容易想到遍历长度时可以从大到小遍历，if (cnt >= k)成立，则该值即为最终结果，可直接break，但最坏时间复杂度没变。

方法二：二分。方法一在[1,max]寻找最大长度时是顺序遍历，由于其有序，我们可借助二分来快速检出结果。如果能截出来k个长度为x的木块，说明答案肯定 >= x，则接下来只需在[x,max]中找m最大满足条件的长度。反之则说明答案 < x，则在[1,x-1]中寻找结果。这样我们每次可以舍弃1/2的情况，因此使用二分的时间复杂度是O(n * log Len)。

public class Main {
    static Scanner in=new Scanner(System.in);
    static int n,k; //n是数组元素的个数，k是我们要截取出来的根子的数量
    static int[] a;
    public static void main(String[] args) {
        n=in.nextInt();k=in.nextInt();
        a=new int[n];
        int l=1,r=0;  //l,r是长度的左右边界，最小是l,即是1，最大是a数组中的单个元素的最大值
        for(int i=0;i<n;i++){
            a[i]=in.nextInt();
            r=Math.max(r,a[i]);
        }
        while(l<r){
            int mid=(l+r+1)/2;
            if(check(mid)>=k) l=mid;  //如果mid满足>=k，我们就可以将mid变大，即l=mid,所以r=mid-1;
            else r=mid-1;
        }
        System.out.println(r);
    }

    public static int check(int mid){ //check函数的返回值是以mid为长度可以截取出来的根子的数量
        int res=0;  //res记录以mid为长度，a数组可以截取出来的根子的数量
        for(int x:a) res+=x/mid;
        return res; //最后返回以mid为长度可以截取出来的根子的数量
    }
}