【计算机图形学】Learning Part Motion of Articulated Objects Using Spatially Continuous NIR
Arxiv上近期刚出的一篇论文:Learning Part Motion of Articulated Objects Using Spatially Continuous Neural Implicit Representations
文章目录
- 1. 为什么要做这篇论文?做这篇论文的目的?
- 2. 这篇论文的Key Idea
- 3. 之前的相关工作(Related Work)
- 4. 问题定义
- 5. Pipeline
-
- Spatial Transformation Grid Generation
-
- Transformation Grid Generation
- Pose Encoder
- Concat G g e o G_{geo} Ggeo and z a r t z_{art} zart to form Spatial Transformation Feature Grid
- Part Motion Generation
- Loss
- 个人对Pipeline的进一步理解
- 6. 实验
-
- 训练类别下测试实例的实验
- 未出现在训练类别中的类别实例实验
- Transformation Grid分析
- 内插、外插实验
- 多部件生成
- 7. 补充
-
- 线性插值
- 双线性插值
- 三线性插值
1. 为什么要做这篇论文?做这篇论文的目的?
在铰接物体的生成方面,以往的方法都只能够handle单一的运动类型,比如顺时针的旋转等等。举个例子,A-SDF就是将整个物体的点云通过网络进行shape和articulation的编码和解码,这种通过网络对点云进行处理的方法没有考虑连接部件的运动限制。又如Ditto,虽然它能够生成不同铰接运动在新视角下的结果,但其依赖于铰接注释,从而限制了它泛化到多种铰接情况下的能力。针对于这些缺陷,作者想要去改善这个问题。
而作者认为,使用神经网络来建模不同种类的部件和铰接类型,对于铰接物体的理解和操纵而言都是非常重要的,希望能够通过一个单一的网络来对多种铰接类型的铰接物体(比如运动类型为旋转和平移的铰接物体)进行运动预测,而不需要其他多余的注释信息。所以论文的目的就是找到这样的一种网络结构。
2. 这篇论文的Key Idea
Key Idea就是引入了一个新的框架来学习铰接物体部件运动空间的连续表示。
作者观察到,part motion是所有铰接物体的核心和通用的一种属性,所以想要通过一个框架来描述铰接部件的运动,从而实现在不需要给定每种物体其他注释信息的情况下,让框架进行泛化,实现对多种部件运动的生成。
具体而言,就是尝试将这种articulation作为一个限制,然后这个限制能够将标量值(pose的姿态,比如门打开的45°,72°等)mapping到一个描述铰接物体部件运动的transformation矩阵。
受到ConvONet的启发,他们建立细粒度的、空间上连续的隐式网格来学习从一个pose到另一个pose的逐点transformations的表示。
3. 之前的相关工作(Related Work)
铰接物体的表示
在理解和建模铰接物体方面的工作包括分割铰接部件,追踪运动轨迹,估计铰接关节的状态和建模运动学结构。但是这些方法都不能够为铰接物体提供显式信息用于下游操作,比如显式的旋转矩阵等等
神经隐式表示
有许多文献致力于神经隐式表示,它们利用深度神经网络来将3D shapes编码成在高分辨率下连续和可微的信号。A-SDF和Ditto也是使用神经网络来建模铰接物体的,但是这两种方法都没有考虑铰接物体的完整性,也就是part motion,这是所有铰接物体的通用属性。在这篇工作中就使用神经隐式表达来建模这个“所有铰接物体的通用属性”(part motion)。
4. 问题定义
学习物体铰接部件的运动至少需要两帧,如果仅有一帧,无法判断物体的运动方向,这会导致ambiguity问题的产生:

输入是同一个物体的两个pose的点云 I 1 I_1 I1和 I 2 ∈ R N × 3 I_2∈R^{N×3} I2∈RN×3( N N N是点云的数量),以及对应的表示pose的标量值 Φ 1 Φ_1 Φ1和 Φ 2 ∈ R Φ_2∈R Φ2∈R,模型的输出会建模它们的部件运动,将铰接的标量值map到其对应的运动结果。进而生成新的部件pose标量值的点云,并且可以通过few-shot生成新的物体类别(我暂时理解为具有相同的铰接部件的新的物体类别)
5. Pipeline
网络由两个部分组成,一个是Spatial Transformation Grid Generation,一个是Part Motion Generation
Spatial Transformation Grid Generation: 铰接物体部件上点移动的分布在3D空间中空间上是连续的,从这一步中构建一个Spatial Transformation Feature Grid G用于表示铰接物体部件运动空间中的连续特征
Part Motion Generation: 根据上面的Spatial Transformation Grid,这里使用三线性插值的方式来获得 I 1 I_1 I1中的点变换到 I 3 I_3 I3的transformation表示。将逐点的变换矩阵 t p t_p tp组合成从点云 I 1 I_1 I1变换到点云 I 3 I_3 I3的完整变换矩阵 T Φ 3 T_{Φ3} TΦ3,进而将变换矩阵应用到 I 1 I_1 I1上获得点云 I 3 ^ \hat{I_3} I3^

Spatial Transformation Grid Generation
该模块用于提取铰接关节运动特征的空间分布。
作者的Key是:铰接部件表面上点的运动,构成了相对于点位置的连续而平滑的分布。
我自己用大白话理解就是:铰接物体中的铰接部件点,它们在pose改变时候所做的铰接运动,是一个连续且平滑的分布,既然这个分布连续,那就说明如果我们建立起了对铰接部件运动的分布,我们就可以通过插值的方式来获得铰接部件运动的信息。因为分布是连续且平滑的,所以使用神经隐式表达来作为点运动的表达是非常合适的。
Transformation Grid Generation
在这个模块,作者希望建立起一个323232的3D grid,均匀采样这个grid中的点,每个点都含有物体几何和铰接部件运动的特征,为了获得这个Grid,在这个模块里面,对于几何的处理是:
G g e o = f g e o ( I 1 , I 2 ) G_{geo}=f_{geo}(I_1,I_2) Ggeo=fgeo(I1,I2)
在这里我想进一步解释一下这个Attention module,但是由于目前还没有Release代码,所以我结合原文猜测一下这个Attention部分的做法:
提取下采样点云 h 1 , h 2 h_1,h_2 h1,h2的特征 ∈ R N ′ × d ∈R^{N^{'}×d} ∈RN′×d, N ′ N^{'} N′是下采样点的数量,接着这部分的输出会进入到一个Attention模块中,我其实目前不是特别了解Attention模块,但是我想了一下我之前看的一篇论文3DShape2VecSet,里面做的事是下采样原本的点云 P P P之后得到新的点云 P ′ P' P′,将新的点云 P ′ P' P′作为Query,原始点云 P P P作为特征集 K , V {K,V} K,V,通过自注意力机制来聚集两个点云的特征
将聚集后的特征通过一个3D-UNet来获得几何的隐式特征Grid G g e o G_{geo} Ggeo,它表示两个输入点云的几何信息
(因为我读论文的经验比较少,我很好奇这里的输入是个什么格式,输出是KKK的Grid,里面的点分别具有自身的几何特征。我猜想这里应该是用体素采样的方法来进行采样的?但是这样的输入又是一种怎样的格式?)
Pose Encoder
这里使用了一个MLP将part pose Φ 1 , Φ 2 , Φ 3 Φ_1,Φ_2,Φ_3 Φ1,Φ2,Φ3标量值映射到 μ 1 , μ 2 , μ 3 ∈ R N × d a r t μ_1,μ_2,μ_3∈R^{N×d_{art}} μ1,μ2,μ3∈RN×dart,也就是将pose的标量信息通过MLP映射成一些articulation features,并通过连接 μ 1 , μ 2 μ_1,μ_2 μ1,μ2来获得 z a r t z_{art} zart,则这里是:
z a r t = f a r t ( Φ 1 , Φ 2 ) z_{art}=f_{art}(Φ_1,Φ_2) zart=fart(Φ1,Φ2)
Concat G g e o G_{geo} Ggeo and z a r t z_{art} zart to form Spatial Transformation Feature Grid
G = [ G g e o , z a r t ] G=[G_{geo},z_{art}] G=[Ggeo,zart]
我感觉这里就是作者的意思是,这个所谓的Spatial Transformation Feature Grid中的每个点的信息,就是由其几何信息和铰接的信息构成的。通过这两个属性构建起了所谓相对于点位置的一个连续而平滑的分布?
Part Motion Generation
在有了Spatial Transformation Feature Grid G G G后,就可以利用这个 G G G来生成从 I 1 I_1 I1到 I 3 I_3 I3空间上连续分布的点运动。
以 μ 3 μ_3 μ3(点云 I 3 I_3 I3的标量pose—— Φ 3 Φ_3 Φ3的特征)为条件,利用三线性插值来获得铰接部件的transformation representation:
Ψ Φ 3 = Q u e r y ( I 1 , G ) Ψ_{Φ3}=Query(I_1,G) ΨΦ3=Query(I1,G)
通过一个MLP来获得每个点应该做的变换 t p t_p tp,每个点应做的变换进一步组合成变换矩阵 T Φ 3 T_{Φ_3} TΦ3:
T Φ 3 = f t r a n s ( Ψ Φ 3 ) T_{Φ_3}=f_{trans}(Ψ_{Φ3}) TΦ3=ftrans(ΨΦ3)
将 T Φ 3 T_{Φ_3} TΦ3运用到 I 1 I_1 I1上得到 I 3 ^ \hat{I_3} I3^: I 3 ^ = T Φ 3 ⋅ I 1 \hat{I_3}=T_{Φ_3}·I_1 I3^=TΦ3⋅I1
通过这种方式,铰接部件上的那些点的运动就可以从空间连续的分布中进行生成,同时保持part在运动后仍然是一个整体,同时保持它们的几何细节。
Loss
使用Earth Mover’s Distance作为损失函数:
L o s s = E M D ( I 3 , I 3 ^ ) Loss=EMD(I_3,\hat{I_3}) Loss=EMD(I3,I3^)
个人对Pipeline的进一步理解
对我而言这里比较难理解的地方就是那个Spatial Transformation Feature Grid,我的理解是通过 I 1 I_1 I1和 I 2 I_2 I2获得了这个物体的几何信息以及不同pose下的信息,进一步建模了物体运动方式在空间中的表示(但是我不理解的地方在于为什么简单将提取的几何信息和articulation的信息进行concat就能够得到这种物体运动方式在空间中的表示,可能是“为了在Feature Grid”中表现出这种信息,前面的Geometry Encoder和Pose Encoder被分别训练出了更高层面的一些信息)。作者有提到,这里的Feature Grid要表征的是铰接部件的空间运动信息。
然后以μ_3为条件,通过三线性插值获得以μ_3为条件下物体运动方式的特征,将这个特征输入MLP获得了具体地transformation矩阵,再应用到输入点云上做transformation。
6. 实验
训练类别下测试实例的实验
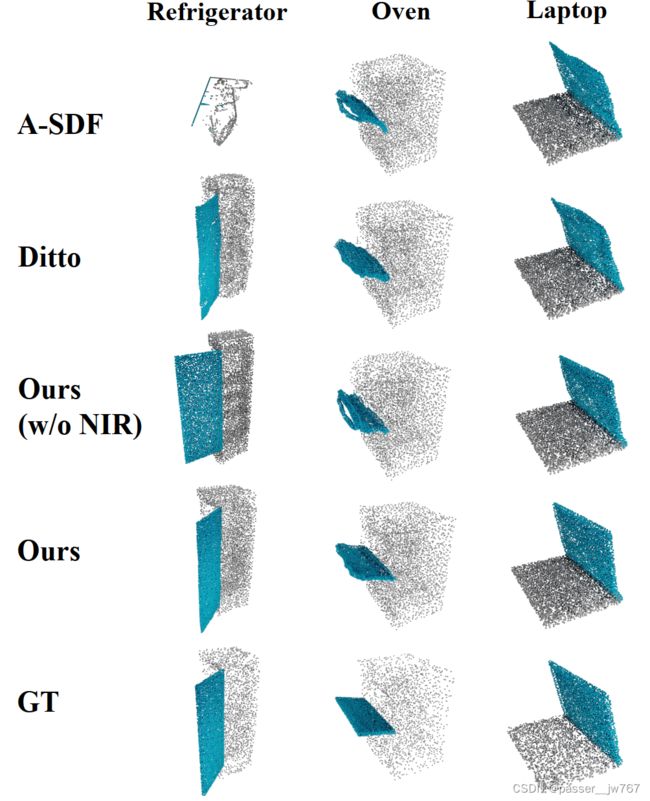
作者认为:Ditto and A-SDF is worse, for example, they both fail to predict the door frame straightly, and fail to predict the microwave door surface smoothly
但是他们的方法保存了更多的几何细节(可能在门、微波炉和剪刀上表现得最为明显)

未出现在训练类别中的类别实例实验
作者认为他们方法比Ditto好在使用了transformation matrix,这个变换矩阵能够表示3D空间中任意类型的运动,对于运动部件的点而言,这种运动在空间上是连续的(我认为例如:90°-45°,这样的角度的变换表现在几何的变换上,在空间中这种变换是连续的)
Transformation Grid分析
冰箱是一个双开门冰箱,所以在3D的变形场下是可以看到左右两侧都有向中间的箭头的,这些箭头象征了铰接物体的axis的运动方向
内插、外插实验
原始物体的part是深绿色和浅绿色,插值结果是介于深、浅之间的绿色

多部件生成
7. 补充
插值相关来源:<插值基础>插值相关
线性插值
这是最简单的一种插值方式,图中红点为a,所表示的值,例如,a在这条线段 x 1 x_1 x1到 x 2 x_2 x2处 30 % 30\% 30%的位置,则值 a = 0.3 a=0.3 a=0.3

双线性插值
这种插值方式实际上就是上面那种插值方式的升级版,之所以称为双线性插值是因为它要做两次插值。
这也很好理解:
在线性插值中,可以想象成对一维的信息进行插值(也就是一条线,求一条线上的某个点);在双线性插值中,可以想象成对二维的信息进行插值(也就是一个平面,求平面中的某个点,则根据这个平面周围的四个点来做插值)

在这里,双线性插值定义为:
先对xy插值,则有 a 1 = ( 1 − α ) x + α y a_1=(1-α)x+αy a1=(1−α)x+αy;再对zw插值,则有 a 2 = ( 1 − α ) z + α w a_2=(1-α)z+αw a2=(1−α)z+αw
再对求得的这两个值在β方向上进行插值: ( 1 − β ) a 1 + β a 2 (1-β)a_1+βa_2 (1−β)a1+βa2,代入上面的式子则有: u = ( 1 − β ) ∗ [ ( 1 − α ) x + α y ] + β [ ( 1 − α ) z + α w ] u=(1-β)*[(1-α)x+αy]+β[(1-α)z+αw] u=(1−β)∗[(1−α)x+αy]+β[(1−α)z+αw]
或者可以先求β方向上的再求α方向上的,那就是: u = ( 1 − α ) ∗ [ ( 1 − β ) x + α z ] + α [ ( 1 − β ) y + α w ] u=(1-α)*[(1-β)x+αz]+α[(1-β)y+αw] u=(1−α)∗[(1−β)x+αz]+α[(1−β)y+αw]
这两种最终都可以整合为: u = ( 1 − α ) ( 1 − β ) x + α ( 1 − β ) y + α β z + ( 1 − α ) β w u=(1-α)(1-β)x+α(1-β)y+αβz+(1-α)βw u=(1−α)(1−β)x+α(1−β)y+αβz+(1−α)βw
使用这三个等价的式子来定义双线性插值,以强调双线性插值可以看做是先对 α α α进行线性插值,然后对 β β β进行线性插值。
三线性插值
通过从单线性插值到双线性插值的理解,我们也可以进一步理解三线性插值,也就是在三维空间中分别在x、y、z轴上进行插值,以下图为例:
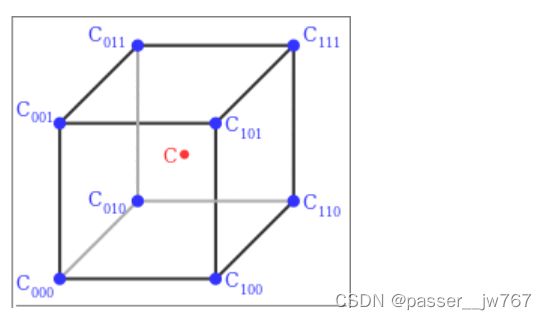
首先在x轴方向上插值,有:

再沿着y轴插值,有:
c 0 = c 00 ( 1 − y d ) + c 10 y d , c 1 = c 01 ( 1 − y d ) + c 11 y d c_0=c_{00}(1-y_d)+c_{10}y_d, c_1=c_{01}(1-y_d)+c_{11}y_d c0=c00(1−yd)+c10yd,c1=c01(1−yd)+c11yd
得到了 c 0 c_0 c0和 c 1 c_1 c1后再在z轴上进行插值:
c = c 0 ( 1 − z d ) + c 1 z d c=c_0(1-z_d)+c_1z_d c=c0(1−zd)+c1zd
