策略梯度方法
文章目录
- 前言
- 一、基于梯度策略的强化学习
-
- policy and value RL
- 基于策略梯度的优劣势
- 目标函数
- 添加基线
- 考虑时序因果关系
- 二、蒙特卡洛策略梯度方法
-
- 实现流程
- 加入基线降低方差
- 三、Actor-Critic Algorithm
-
- 目标函数
- 线性TD(0)结合策略梯度的简单AC算法
- 一些改进
-
- 基于AC框架加入基线降低方差
- 基于n-step TD的AC框架
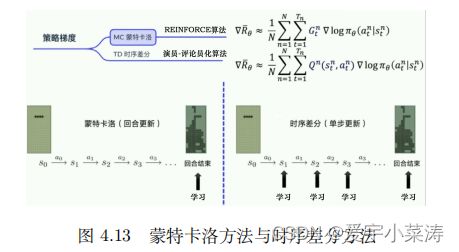
- MC与TD的策略梯度方法的不同
前言
策略梯度学习,介绍基于价值与基于策略的RL,如何基于策略梯度进行优化,包括AC框架的介绍。
策略梯度算法是基于策略的方法,其对策略进行了参数化。假设参数为 θ \theta θ的策略为 π θ \pi_\theta πθ,该策略为随机性策略,其输入某个状态,输出一个动作的概率分布。策略梯度算法不需要在动作空间中最大化价值,因此较为适合解决具有高维或者连续动作空间的问题。
一、基于梯度策略的强化学习
将策略 π \pi π参数化,即给定状态后通过策略函数得到每个动作执行的概率,策略函数实际上是概率分布函数,相比于基于价值的强化学习有所不同,后者是采用贪婪算法进行策略改进,缺少一点的探索性,而将策略参数化后,每个动作都有了不同的执行的概率。

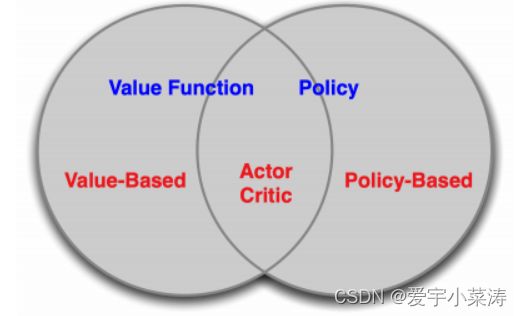
policy and value RL
基于价值函数的RL方法:学习价值函数,通过价值函数隐式的学习策略
基于策略的RL方法:直接学习策略的分布,不考虑价值函数
AC框架:结合policy and value
基于策略梯度的优劣势
优势:具有更高的收敛性,一定能收敛到全局或局部最优、在高维的动作空间更加有效、能够真正的学习到随机的策略
劣势:具有较高的方差、效率不高(采取一定的方法可以进行改进)
目标函数
当我们获得一组轨迹后
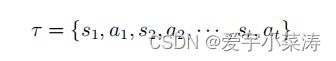
给定策略函数的参数后,便可以计算某个轨迹的发生概念,首先计算环境 s 1 s_1 s1的概率,通过策略函数计算动作 a 1 a_1 a1的概率,持续计算下去,便得到这个轨迹的概率

每个轨迹具有回报,我们要计算所有轨迹的奖励,优化策略参数,使得整体回报的期望最大
![]()
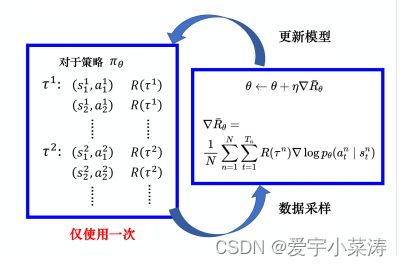
若想将整体回报的期望最大化,采用梯度上升来最大化,所以接下来要对整体回报的期望求导,在求导之前将策略函数的导数转化为log形式,有助于后续的求导。

因此整体回报的期望导数可以写成下列的形式

经过下列推导可以得到最终的优化形式

理解:在采样到的数据里面,采样到在某一个状态 s t s_t st要执行某一个动作 a t a_t at, ( s t s_t st , a t a_t at)是在整个轨迹的里面的某一个状态和动作的对。假设我们在 s t s_t st 执行 a t a_t at,最后发现轨迹的奖励是正的,我们就要增加在 s t s_t st执行 a t a_t at的概率。反之,则减少其发生的概率。
采用梯度更新的方式进行参数更新
即使策略梯度更新的方式是无偏的但具有较大的方差,采用一些tricks降低方差:添加基线、加入时序因果关系
添加基线
假设动作a、b、c都能带来奖励,而a、b所带来的奖励很少、c带来的奖励很多,因此要增加c动作的概率,但奖励都是正的,无法将c的增加概率最大化,因此采用加入基线的方法,将小奖励的动作所获的奖励变为负,这样奖励有正有负,就可以最大限度的提高奖励最大的动作的概率。
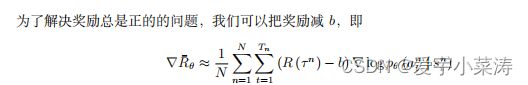
考虑时序因果关系
优化目标函数时,考虑整个episode的奖励,如果出现其中某个动作带来的奖励大,但整个episode带来的奖励小,因此就抑制了带来奖励大的动作出现的概率,因此可以在t时间步只考虑t时间步后的奖励,这样在更新时,每个动作不会受到前面动作的影响。
二、蒙特卡洛策略梯度方法
实现流程

基于MC方法的策略梯度:MC的方法是基于完整的episode进行数据采样,所有要先完成一个回合后,再利用这个回合的数据进行训练。
获得整个episode的数据
![]()
基于目标函数进行更新, G t G_t Gt是代表t时候之后的未来总的奖励


加入基线降低方差
三、Actor-Critic Algorithm
目标函数
尽管基于MC的策略梯度无偏差,但具有较大的方差,如果能够准确的估计价值函数,用来指导策略的更新,就能够有效降低方差。AC框架结合策略梯度与TD的方法,能够实现单步更新。

因此AC框架的主要包括两部分内容:
Critic:参数化动作价值函数 Q w ( s t , a t ) Q_w (s_t,a_t) Qw(st,at)
Actor:根据 Q w ( s t , a t ) Q_w (s_t,a_t) Qw(st,at)进行更新策略函数的参数
因此AC需要保存两组参数,动作价值函数与策略函数
线性TD(0)结合策略梯度的简单AC算法
具体流程:

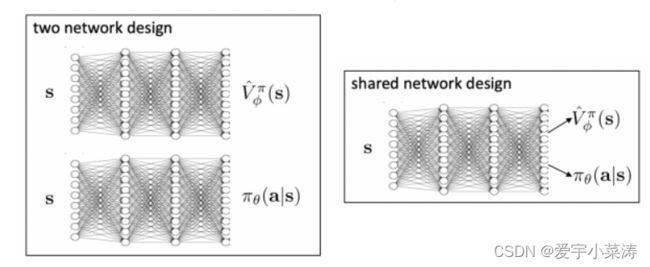
AC网络结构的设计,可以单独维护两个网络,也能够共享特征提取部分,设计两个头输出作为动作价值函数与策略函数
一些改进
基于AC框架加入基线降低方差
动作价值函数是在给定策略下,采用某一动作带来的累积奖励的期望,衡量动作的价值

状态价值函数是给定策略下,在某个状态下与环境进行交互获得累积奖励的期望,衡量某个状态的价值

因此将状态价值函数当作基线加入到目标函数中进行优化能够降低方差

其中 A π , γ ( s , a ) A^{\pi,\gamma(s,a)} Aπ,γ(s,a)代表优势函数。