k近邻算法(KNN)原理小结
提示:本篇文章是参考刘建平老师的博客,该文章只是作为个人学习的笔记.
K近邻法(KNN)原理小结 - 刘建平Pinard - 博客园 (cnblogs.com)
文章目录
前言
一、KNN算法三要素
1.既然有了k个最近邻居那么如何判断样本分类呢?
2.k个是几个?
(a).这个k选择很小的时候会发生什么?
(b).这个k选择很大的时候会发生什么?
最近邻居,这个最近的度量是什么?
二、KNN暴力解法
三、KNN算法之KD树实现原理
1.KD树的建立
2.KD树搜索最近邻
3..KD树的预测
四、球树的建立
1.球形树的建立
2.球树搜索最近邻
总结
前言
K近邻法(k-nearest neighbors,KNN)是一种很基本的机器学习方法了,在我们平常的生活中也会不自主的应用。俗话说"人以类聚,物以群分",要想判断一个人的人品怎么样,就只需知到在他身边的人的人品,这就用到了KNN的思想,KNN方法既可以做分类,也可以做回归,这点和决策树算法相同。
KNN做回归和分类的主要区别在于最后做预测时候的决策方式不同。KNN做分类预测时,一般是选择多数表决法,即训练集里和预测的样本特征最近的K个样本,预测为里面有最多类别数的类别。而KNN做回归时,一般是选择平均法,即最近的K个样本的样本输出的平均值作为回归预测值。由于两者区别不大,虽然本文主要是讲解KNN的分类方法,但思想对KNN的回归方法也适用。
注意:在学习任何算法之前不能简单生搬硬套,要懂得算法的内在本质将其应用到适合的地方,才能达到好的效果.在文章我会总结出自己在学习的时候对算法的理解.
一、KNN算法三要素
这三要素其实应该在了解KNN算法的基本思想的基础上在来谈会更好,更深入的理解.如果一点没接触KNN算法的话可以先了解一下这三要素,KNN其实是一个很容易理解的算法大家不要有压力.
KNN算法我们主要要考虑三个重要的要素,对于固定的训练集,只要这三点确定了,算法的预测方式也就决定了。这三个最终的要素是k值的选取,距离度量的方式和分类决策规则。
对于分类决策规则,一般都是使用前面提到的多数表决法。所以我们重点是关注与k值的选择和距离的度量方式。
这三要素互相联系,下面是我对这种联系的自身理解.
首先通过KNN算法(k-nearest neighbors)翻译过来就是k个最近的邻居算法,这就涉及到了三个问题,首先,k个是几个?其次最近邻居,这个最近的度量是什么?最后,既然有了k个最近邻居那么如何判断样本分类呢?
搞懂这三个问题就会深入理解KNN算法
1.既然有了k个最近邻居那么如何判断样本分类呢?
答:对于分类决策规则,一般都是使用多数表决法。这个多数表决法其实就是像投票一样,投的票数多就把样本分到那一类,这个还是比较好理解的,具体还有什么分类决策规则我也没具体研究,如果需要的话我就放到评论区.
2.k个是几个?
答:对于k值的选择,没有一个固定的经验,一般根据样本的分布,选择一个较小的值,可以通过交叉验证选择一个合适的k值。这个交叉验证如果有小伙伴不懂,我后期再出一篇文章帮助大家理解.
关于这个k我还要提几个小问题
(a).这个k选择很小的时候会发生什么?
答:选择较小的k值,就相当于用较小的领域中的训练实例进行预测,训练误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是泛化误差会增大,换句话说,K值的减小就意味着整体模型变得复杂,容易发生过拟合;
k取较小,我们假设为1,那么决策时只根据这一个最近的邻居就判断样本的类别,就有点太绝对了,比如你有一个外国室友,寝室就你们两个人,你离他最近就判断你是外国人,这明显不太合理,毕竟你身边大多数都是国人,这样大家就好理解了.
(b).这个k选择很大的时候会发生什么?
选择较大的k值,就相当于用较大领域中的训练实例进行预测,其优点是可以减少泛化误差,但缺点是训练误差会增大。这时候,与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误,且K值的增大就意味着整体的模型变得简单。
一个极端是k等于样本数m,则完全没有分类,此时无论输入实例是什么,都只是简单的预测它属于在训练实例中最多的类,模型过于简单。
最近邻居,这个最近的度量是什么?
这个距离后续可能会出一期关于所有距离的介绍,帮助小伙伴更好的理解,先理解这几个就可以了.
二、KNN暴力解法
通过上面的介绍应该对KNN进行初步的理解,我们开始讨论KNN算法的实现方式
既然我们要找到k个最近的邻居来做预测,那么我们只需要计算预测样本和所有训练集中的样本的距离,然后计算出最小的k个距离即可,接着多数表决,很容易做出预测。这个方法的确简单直接,在样本量少,样本特征少的时候有效。但是在实际运用中很多时候用不上,为什么呢?因为我们经常碰到样本的特征数有上千以上,样本量有几十万以上,如果我们这要去预测少量的测试集样本,算法的时间效率很成问题。因此,这个方法我们一般称之为蛮力实现。比较适合于少量样本的简单模型的时候用。
既然蛮力实现在特征多,样本多的时候很有局限性,那么我们有没有其他的好办法呢?有!这里我们讲解两种办法,一个是KD树实现,一个是球树实现。
三、KNN算法之KD树实现原理
KD树算法没有一开始就尝试对测试样本分类,而是先对训练集建模,建立的模型就是KD树,建好了模型再对测试集做预测。所谓的KD树就是K个特征维度的树,注意这里的K和KNN中的K的意思不同。KNN中的K代表最近的K个样本,KD树中的K代表样本特征的维数。为了防止混淆,后面我们称特征维数为n。
KD树算法包括三步,第一步是建树,第二部是搜索最近邻,最后一步是预测。
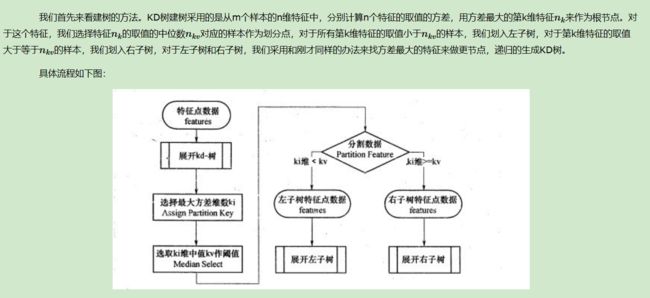
1.KD树的建立
这里有篇知乎文章帮助大家理解我第一次没有理解,仔细读一下就能理解了.这篇文章根刘建平老师的博客操作上有点区别但大致思想相同.
【数学】kd 树算法之详细篇 - 知乎 (zhihu.com)
刘建平老师博客
这种对算法直接描述看着会晕,建议直接看例子.
刘建平老师的算法就是每次找方差最大的那个维度进行划分并且划分节点选择中位数的节点这样保证分类样本更均衡些.我在第一次读的时候的确可以理解,但在后续搜索最邻近的时候出现了一个疑惑,就是既然按照方差划分的,那么每次划分都需要记录一下以什么维度划分,否则后续寻找的时候会发生困难,所以我看了知乎的那篇文章.
知乎文章
与刘建平老师的博客相比这篇文章在划分是是交替进行的而不是用方差大的来进行划分,先选择x后选择y交替进行,这样在后续查找的时候比较好找只需知到每层按什么划分的就行了.而刘建平老师需知道每个节点的划分情况,这是我自己的理解,如果有什么错误的地方,请评论取指正.谢谢
2.KD树搜索最近邻
上面就是刘建老师的博客,第一次读的时候我又蒙了,后来通过自己的理解终于搞懂为什么这么做了.
大家也可以阅读上面知乎的那篇文章,大家读完再来理解我的话会更好,文章的具体细节我就不再这里展示了只表达我对这算法的理解.
首先不管是刘建平老师的还是那篇知乎文章,首先给你个样本让你找到k个最近的邻居,第一步就要根据样本以及树的划分找到样本所在树的区域,也就是找到其区域对应的叶子节点,形成搜索路径,因为这个kd树,你类比一下排序二叉树一样在查找时会大大减少比较次数(如果对排序二叉树不了解可以忽略这一段),之后设置一个最近邻居集合,你要找k个,那么最终结果就是数据中最近的k个样本点,那么如何找呢?
我的理解就是遍历可能与其最近的节点,找到k个就完事了.大家看我的理解一定要提前看这两篇博客理解大致的方法.我只讨论刘建平老师的博客与知乎的做法不同,虽然做法不同但思想是相同的.
两篇文章在搜索最近邻时要查另一个分支的情况做法不同
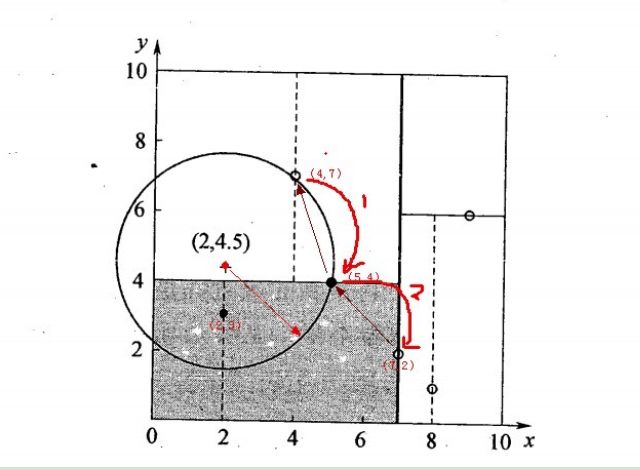
刘建平老师是根据待测样本作为圆心与相对距离较近的数据点的距离作为半径画一个圆,如果这个圆与划分线相交则就需要查另一个分支,因为另一个分支可能有与他更近的数据点.
知乎文章则是将待测样本点与划分线的距离设为:D1与相对距离较近的数据点的距离设为D2相比较如果D2>D1那么说明另一个分支可能有与他更近的数据点.
其实这两种做法本质是一样的.
我们知道每一次划分虽然划分的是左右子树,其实划分的是区域,千万不要把这两个关系独立起来.
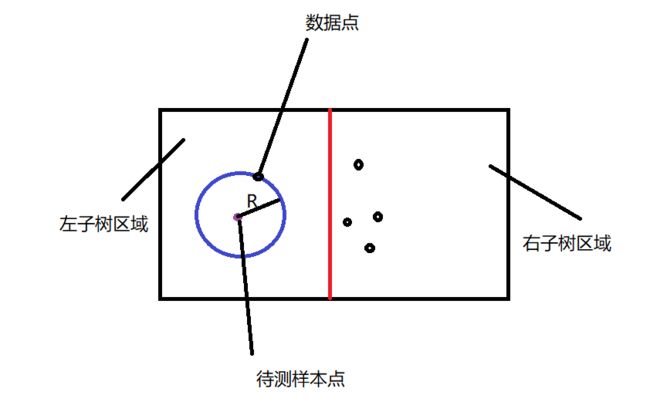
我画个简单的图帮助大家理解.
像这种情况说明右子树肯定没有更近的点了所以就不用搜索.
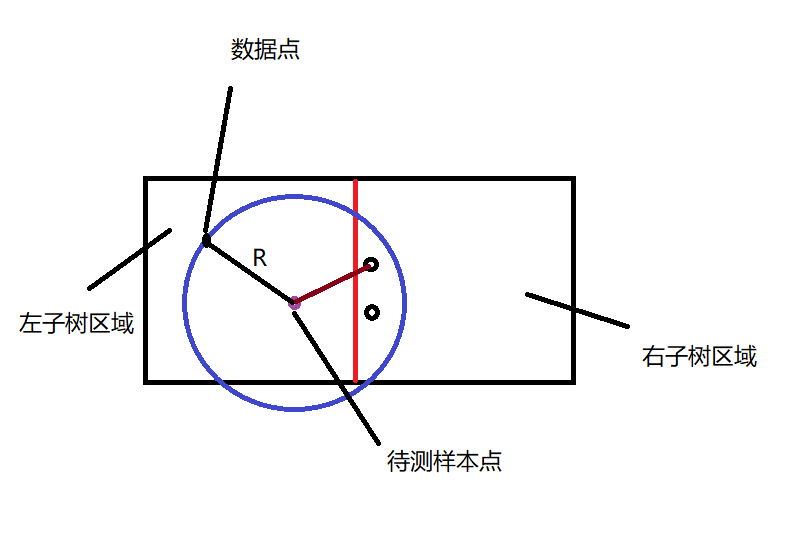
这样一看右子树可能存在更近的点,就需要进行搜索.这样画圆其实也就是将待测样本点与划分线的距离设为:D1与相对距离较近的数据点的距离设为D2相比较.
3..KD树的预测
有了KD树搜索最近邻的办法,KD树的预测就很简单了,在KD树搜索最近邻的基础上,我们选择到了第一个最近邻样本,就把它置为已选。在第二轮中,我们忽略置为已选的样本,重新选择最近邻,这样跑k次,就得到了目标的K个最近邻,然后根据多数表决法,如果是KNN分类,预测为K个最近邻里面有最多类别数的类别。如果是KNN回归,用K个最近邻样本输出的平均值作为回归预测值。
四、球树的建立
只要理解我上面的,那么这个就不在话下了.就是将区域划分成球形
1.球形树的建立
2.球树搜索最近邻
使用球树找出给定目标点的最近邻方法是首先自上而下贯穿整棵树找出包含目标点所在的叶子,并在这个球里找出与目标点最邻近的点,这将确定出目标点距离它的最近邻点的一个上限值,然后跟KD树查找一样,检查兄弟结点,如果目标点到兄弟结点中心的距离超过兄弟结点的半径与当前的上限值之和,那么兄弟结点里不可能存在一个更近的点;否则的话,必须进一步检查位于兄弟结点以下的子树。
检查完兄弟节点后,我们向父节点回溯,继续搜索最小邻近值。当回溯到根节点时,此时的最小邻近值就是最终的搜索结果。
从上面的描述可以看出,KD树在搜索路径优化时使用的是两点之间的距离来判断,而球树使用的是两边之和大于第三边来判断,相对来说球树的判断更加复杂,但是却避免了更多的搜索,这是一个权衡。
总结
KNN算法是很基本的机器学习算法了,它非常容易学习,在维度很高的时候也有很好的分类效率,因此运用也很广泛,这里总结下KNN的优缺点。
KNN的主要优点有:
1) 理论成熟,思想简单,既可以用来做分类也可以用来做回归
2) 可用于非线性分类
3) 训练时间复杂度比支持向量机之类的算法低,仅为O(n)
4) 和朴素贝叶斯之类的算法比,对数据没有假设,准确度高,对异常点不敏感
5) 由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合
6)该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分
KNN的主要缺点有:
1)计算量大,尤其是特征数非常多的时候
2)样本不平衡的时候,对稀有类别的预测准确率低
3)KD树,球树之类的模型建立需要大量的内存
4)使用懒散学习方法,基本上不学习,导致预测时速度比起逻辑回归之类的算法慢
5)相比决策树模型,KNN模型可解释性不强
最后由于本人时间原因,而且该文章只作为个人笔记,许多借鉴的地方请谅解.