U4_2 语法分析-自底向上分析-算符优先分析

一、回顾

1、推导 vs 规约

1. 自顶向下（Top-Down）分析：推导（Derivations）
   若$Z={>}^{+}S则S\in L(G[Z])否则S\notin L(G[Z])$
2. 自底向上（Bottom-Up）分析：规约（Reductions）
   若$Z<{=}^{+}S则S\in L(G[Z])否则S\notin L(G[Z])$

2、句型、短语、简单短语、句柄

句型：$Z=>x,且x\in V^{\ast }$

$给定文法G[Z],w=xuy\in V+，为该文法的句型$

$若Z=={>}^{\ast }xUy,且U=={>}^{+}u,则u是句型w相对于U的$短语；

$若Z=={>}^{\ast }xUy,且U==>u,则u是句型w相对于U的$简单短语。

$其中U\in V_n，u\in V^{+}，x,y\in V^{\ast }$

$任一句型的最左简单短语称为该句型的$句柄。

二、自底向上（移进-规约）分析方法

1、基本思想

采用自左向右分析输入串,那么自底向上分析：

1. 从输入符号串开始，通过不断查找当前句型的句柄(最左简单短语)，并利用有关规则进行归约
   若句子能归约为文法的识别符号，则表示分析成功，输入符号串是文法的合法句子。
   若不能规约成功，否则有语法错误。

2、分析过程

1. 找出当前句型的句柄 x （或句柄的变形）
2. 找出以 x 为右部的规则 X::= x
3. 把 x 归约为X，（自下而上）产生语法树的一枝
   关键：找出当前句型的句柄 x (或其变形）

3、移进—归约分析（Shift-Reduce Parsing)

建立符号栈，用来记录分析的历史和现状，并根据所面临的状态，确定下一步动作是移进还是归约。

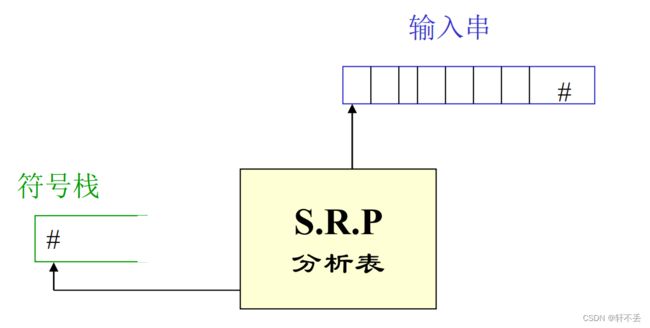
1. 把输入符号串按扫描顺序一一地移进符号栈（一次移一个）
2. 移进过程中，检查栈中符号，当在栈顶的若干符号形成当前句型的句柄时，就根据规则进行归约：
   将句柄从符号栈中弹出，并将相应的非终结符号压入栈内（即规则的左部符号）。
   然后再检查栈内符号串是否形成新的句柄，若有就再进行归约，否则移进符号。
3. 分析一直进行到读到输入串的右界符为止。最后，若栈中仅含有左界符号和识别符号，则表示分析成功，否则失败。
   例子：
   
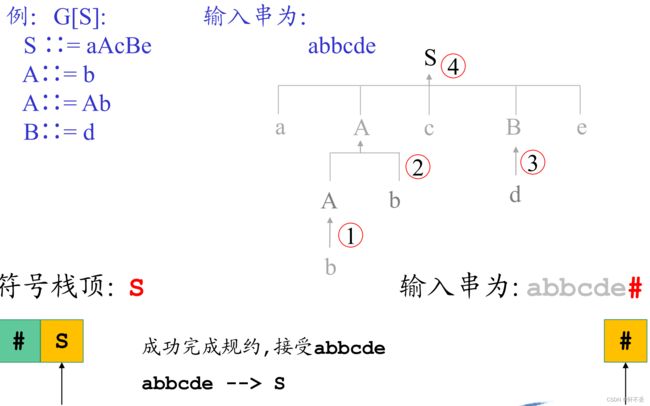
   这个流程的关键就是确定当前的句柄

三、算符优先分析

1、概念

这是一种经典的自底向上分析法，简单直观，并被广泛使用，开始主要是对表达式的分析，现在已不限于此。可以用于一大类上下无关的文法。

称为算符优先分析是因为这种方法是仿效算术式的四则运算而建立起来的，作算术式的四则运算时，为了保证计算结果 和过程的唯一性，规定了一个统一的四则运算法则，规定运 算符之间的优先关系。

运算规则：

1. 乘除的优先级大于加减
2. 同优先级的运算符左大于右
3. 括号内的优先级大于括号外

算符优先分析的特点：仿效四则运算过程，预先规定相邻终结符之间的优先关系，然后利用这种优先关系来确定句型的“句柄”，并进行归约

分析器结构：

2、分析流程

1）先确定终结符之间的优先关系

定义：设 a, b 为可能相邻的终结符

1. $a=b$      a的优先级等于b （栈内a、栈外b抵消）
2. $a<b$       a的优先级小于b （栈外b移进）
3. $a>b$       a的优先级大于b （栈内a规约）

相邻的意思很宽泛，越过非终结符看也可以

3、算符优先文法

1）概念

若文法中无形如$U::=\cdot \cdot \cdot VW\cdot \cdot \cdot$的规则，这里$V,W\in Vn$则称$G$为$OG$文法，也就是算符文法。
中间一定要有终结符间隔

2）优先关系的定义

1. $a=biff文法中有形如U::=\cdot \cdot \cdot ab\cdot \cdot \cdot 或U::=\cdot \cdot \cdot aVb\cdot \cdot \cdot 的规则。$
2. $a<biff文法中有形如U::=\cdot \cdot \cdot aW\cdot \cdot \cdot 的规则，其中W=>b\cdot \cdot \cdot 或W=>Vb\cdot \cdot \cdot$
3. $a>biff文法中有形如U::=\cdot \cdot \cdot Wb\cdot \cdot \cdot 的规则,其中W=>\cdot \cdot \cdot a或W=>\cdot \cdot \cdot aV$

3）确定关系的步骤

1. 先看有没有$=$的出现，即两个终结符夹着非终结符或者两个终结符同时出现。
2. 找到每个非终结符，比较左右两边的非终结符

4）求“ <. . ”、“ > ”

需定义两个集合：
$FIRSTVT(U)=${$b|U={>}^{+}b\dots 或U={>}^{+}Vb\dots ,b\in V_t,V\in V_n$}

$LASTVT(U)=$ {$a|U={>}^{+}\dots a或U={>}^{+}\dots aV,a\in V_t,V\in V_n$}

则：
$W::=...aU...，对任何b,b\in FIRSTVT(U)，a<b$
$W::=...Ub...，对任何a,a\in LASTVT(U)，a>b$

构造$FIRSTVT(U)$的算法

1. $若有规则U::=b\dots 或U::=Vb\dots (存在U={>}^{+}b\dots 或U={>}^{+}Vb\dots )则b\in FIRSTVT(U)$
2. $若有规则U::=V\dots 且b\in FIRSTVT(V),则b\in FIRSTVT(U)$

构造$LASTVT(U)$的算法原理一样
3. $若有规则U::=\dots a或U::=\dots aV,则a\in LASTVT(U)$
4. $若有规则U::=\dots V,且a\in LASTVT(V),则a\in LASTVT(U)$

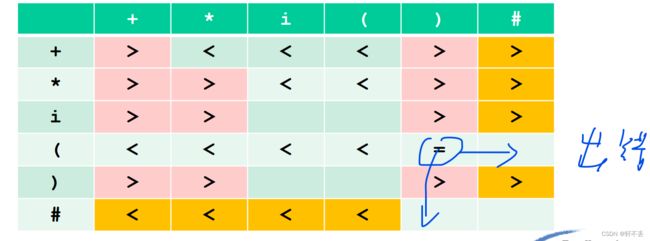
5）构造优先表的算法

1. 扫描每一条规则，如果有 U::=…ab… |…aVb… 设置 a=b
2. 扫描，如有 $U::=..aV$ , 设置$a<b$, 对 $b\in FIRSTVT${$V$}
3. 扫描，如有 $U::=..Va$ , 设置$b>a$, 对 $b\in LASTVT${$V$}
4. 对#特殊处理，横行#小于，纵行大于，碰到等号不填（出错）
   

6）小总结

算符优先文法（OPG）的定义：
设有一OG文法，如果在任意两个终结符之间，至多只有上述关系中的一种，则称该文法为算符优先文法(OPG)。即不会出现二义性，两个终结符之间有两个优先级关系

算符优先分析算法的实现
本质上就是先定义优先级，在分析过程中通过比较相邻运算符之间的优先级来确定**句型的“句柄”**并进行归约。

但是根据运算优先级确定的句柄和之前所定义的句柄不同，因此必须要有终结符从中间参与，因此定义素短语：
素短语：文法G的句型的素短语是一个短语，它至少包含有一个终结符号，并且除它自身以外不再包含其他素短语。

只有TF和i为素短语,其中TF为最左素短语,而该句型句柄为T。

画出优先级图，找到最左素短语

4、总结

每次归约最左子串,确实是当前句型的最左素短语(语法树）。
归约的不都是真句柄（仅i归约为F是句柄，但它是最左素短语)。
没有完全按规则进行归约,因为素短语不一定是简单短语。