机器学习与模式识别

参考教材：《机器学习》清华大学出版社 周志华；
代码部分建议使用jupyter notnook进行逐句的验证，练习
学习记录内容，若有不对，欢迎留言指正。
持续更文中……

第一章 绪论

1.区分回归、聚类、分类任务

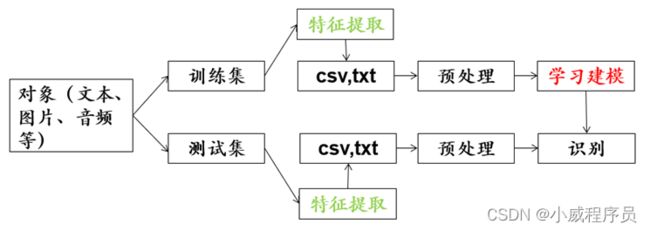
2.机器学习的一般过程

3.假设空间的确定，版本空间的含义

假设空间的计算：(*+n属性) (+n属性)…… (+n属性）+ 1
对“1”的理解： 定义好坏的前提可能都是不存在的概念，我们常常用空集来表示这个假设。
版本空间： 一个与训练集一致的假设集合
Ps：训练集、验证集、测试集、交叉验证基本概念理解

第二章 模型评估与选择

1.欠拟合和过拟合概念的理解

欠拟合：不能很好的捕捉到数据特征，模型在训练集上误差高。
过拟合：学习的太彻底，噪声特征也学习了，模型在训练集上误差低，验证集上误差高。

2.模型的评估方法

(1) k折交叉验证

把原始训练数据集分为k份（不重合），然后做k次模型的训练和验证。每一次选一个作为验证集，其余k-1个子集作为训练集使用。

(2) 留一法（n折交叉验证）

与k折交叉验证不同，这里的n指的是样本的数目，即每次用一个样本做验证集，其余n-1个样本做训练集。

(3) 代码实例——鸢尾花数据集

项目简介：鸢尾花数据集（Iris）是一个经典数据集。数据集内包含 3 类共 150 条记录，每类各 50 个数据，每条记录都有 4 项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度，可以通过这4个特征预测鸢尾花卉属于（iris-setosa, iris-versicolour, iris-virginica，山鸢尾、变色鸢尾和维吉尼亚鸢尾三个类别）中的哪一品种。
鸢尾花数据集官网下载链接

# 准备数据集
from sklearn import datasets
X,y=datasets.load_iris(return_X_y=True)
#生成训练集和测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=7)
'''
X_train,X_test,y_train,y_test=train_test_split(train_data,train_target,test_size,random_state)
test_size(): 划分的比例，例test_size=0.2 表示数据集的20%划分为测试集，其余为训练集
'''
#训练
from sklearn.linear_model.logistic import LogisticRegression
model=LogisticRegression()    #逻辑回归模型
model.fit(X_train,y_train)
#预测
y_predict=model.predict(X_test)
from sklearn.metrics import accuracy_score   #accuracy_score() 求所有分类正确的百分比
print(accuracy_score(y_test,y_predict))
'''
sklearn.metrics.accuracy_score(y_true, y_pred, normalize=True, sample_weight=None)
normalize：默认值为True，返回正确分类的比例；如果为False，返回正确分类的样本数
'''
#k折交叉验证
from sklearn.model_selection import KFold,cross_val_score
kf = KFold(10)
result = cross_val_score(model,X_train,y_train,cv=kf,scoring='accuracy')
result.mean()
'''
KFold(n_split=10,shuffle=False,random_state=None)（折数，是否打乱数据顺序，随机数种子）
cross_val_score(estiamtor,X_train,y_train,scoring=' ',cv=  )（交叉验证算法，，样本标签，评价指标，交叉验证数或可迭代的次数）
'''
#留一法
from sklearn.model_selection import LeaveOneOut
loocv=LeaveOneOut()
result=cross_val_score(model,X_train,y_train,cv=loocv,scoring='accuracy')
result.mean()

3.衡量回归的性能指标

(1) 公式

均方误差：

均方根误差：

平均绝对误差：

例题一道：
假设你有以下数据:输入和输出都只有一个变量。使用线性回归模型(y=wx+b)来拟合数据。那么使用留一法(Leave-One Out)交叉验证得到的均方误差是多少? （ 49/27 留一法 + MSE公式）

输入x	输出y
0	2
2	2
3	1

决定系数: 模型好坏的决定系数 $R^2$

分子:需要衡量的模型
分母:基准模型(将均值作为预测值)
(1)$R^2$=1,模型对所有的数据预测准确,模型的性能最优;
(2)$R^2$=0,模型的性能与基准模型相同;
(3)$R^2$<0,模型的性能低于基准模型。

(2) 代码实现

from sklean.metrics import
mean_absolute_error(y_true,y_predict)        #平均绝对误差
mean_squared_error(y_true,y_predict)         #均方根误差
r2_score(y_true,y_predict)                   #决定系数

4.衡量分类任务的性能指标

精度：分类正确的样本数 / 样本总数

accuracy_score(y_true,y_predict)

混淆矩阵的构建

真实\预测	0	1
0	TN	FP
1	FN	TP

from sklearn.metrics import confusion_matrix
confusion_matrix(y_true,y_predict)

(1) 查准率

$$Precision=\frac{TP}{TP+FP}$$
通俗理解：
预测为正例真实为正例 占 预测结果为正例的比例，即预测正例里面的准确率

from sklearn.metrics import precision_score
precision_score(y_true,y_predict)

(2) 查全率

$$Recall=\frac{TP}{TP+FN}$$
召回率 ，即真实正例中的准确率

from sklearn.metrics import recall_score
recall_score(y_true,y_predict)

(3) F1度量

同时兼顾查准率与查全率的F1度量：
$$F1=\frac{2PR}{P+R}$$

β>0度量了查全率对查准率的相对重要性;
β=1退化为标准F1度量
β>1查全率更重要
β<1查准率更重要。

from sklearn.metrics import f1_score
f1_score(y_true,y_predict)

(4)假正例率

$$FPR=\frac{FP}{FP+TN}$$
真反预测为正占真反的比例

(5)真正例率

$$TPR=\frac{TP}{FN+TP}$$
真正预测为正占真正的比例

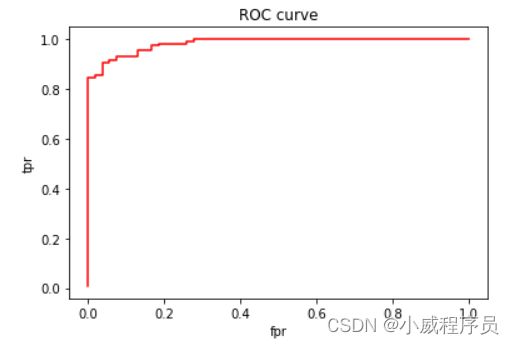
(6)ROC曲线

POC曲线：FPR为横轴，TPR为纵轴
意义：
体现其期望泛化性能的好坏 。凸起越高，模型准确率越高。

(7) AUC

一般情况下，AUC越大，模型越好。
两种求法：
1，ROC曲线下方与x轴围成的面积
2，利用公式进行计算

from sklearn.metrics import roc_auc_score
roc_auc_score(y_true,y_predict)

例题一道：
求其 AUC

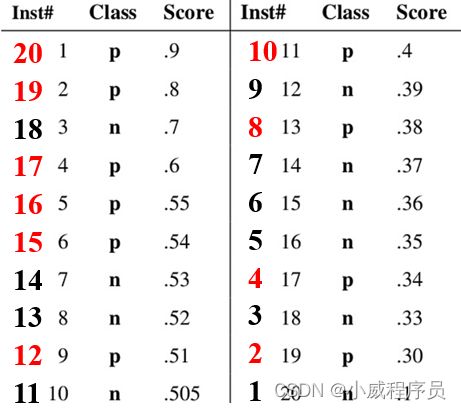
ROC曲线：

公式求法过程为：
由于预测概率顺序已经排好，所以公式中的${\sum }_{iepositiveclass}ran{k}_i=123$,红色序号之和
所以$$AUC=\frac{123-\frac{10\ast (10+1)}{2}}{10\ast 10}=0.68$$

代码实例-乳腺癌数据集

乳腺癌数据集官网链接（访问较慢）
数据集中：每个图像文件名都存储了关于图像本身的信息:活检方法、肿瘤级别、肿瘤类型、患者识别和放大系数。例如，SOB_B_TA-14-4659-40-001.png是一个管状腺瘤型良性肿瘤的图像1，放大倍数为40倍，来自于14-4659玻片，由SOB程序收集。

# 1、准备数据（载入数据）
from sklearn import datasets
X,y=datasets.load_breast_cancer(return_X_y=True)
# 2、生成训练集和测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3,random_state=4)
# 3、训练
from sklearn.linear_model.logistic import LogisticRegression
model=LogisticRegression()
model.fit(X_train,y_train)
# 4、预测
y_predict = model.predict(X_test)
y_score = model.predict_proba(X_test)[:,1]
# 5、评估
## 5.1 精度
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test,y_predict))
## 5.2 混淆矩阵
from sklearn.metrics import confusion_matrix
print(confusion_matrix(y_test,y_predict))
## 5.3 查准率，查全率，f1_score
from sklearn.metrics import precision_score,recall_score,f1_score
print(precision_score(y_test,y_predict))
print(recall_score(y_test,y_predict))
print(f1_score(y_test,y_predict))
## 5.4 PR曲线
from sklearn.metrics import precision_recall_curve
p,r,t=precision_recall_curve(y_test,y_score)
import matplotlib.pyplot as plt
plt.plot(r,p,'b')
plt.xlabel('recall')
plt.ylabel('precision')
plt.title('PR curve')
plt.show()

## 5.5ROC曲线
from sklearn.metrics import roc_curve,roc_auc_score
fpr,tpr,t=roc_curve(y_test,y_score)
plt.plot(fpr,tpr,'r')
plt.xlabel('fpr')
plt.ylabel('tpr')
plt.title('ROC curve')
plt.show()

print(roc_auc_score(y_test,y_score))

第三章 线性模型

1，线性模型的知识储备

凸函数、特征值与特征向量、损失函数（用来衡量拟合程度的好坏）、偏导
线性回归的损失函数：均方差损失函数
逻辑回归的损失函数：对数损失函数
基本模型中的最佳参数：
$$w^{\ast }=(X^{T}X{)}^{-1}{X}^{T}y$$
线性模型的基本形式实现代码：

## 1.1读取模拟数据ex0_1.csv
from pandas import read_csv
df=read_csv('ex0_1.csv',header=None) #标题行，header
data=df.values
#输入输出分离
X=data[:,0].reshape((-1,1))
y=data[:,1].reshape((-1,1))
## 1.2 绘制散点图
import matplotlib.pyplot as plt
plt.scatter(X,y)
plt.show()
## 1.3正规方程解 inv(X.T * X ) * X.T * y
import numpy as np
#求X增广矩阵
ones=np.ones((X.shape[0],1))
X_ones = np.hstack((ones,X))

XT=X_ones.T                #求X转置
XTX=np.dot(XT,X_ones)
XTX_1=np.linalg.inv(XTX)
XTX_1XT=np.dot(XTX_1,XT)
W=np.dot(XTX_1XT,y)
## 1.4 绘制拟合的直线
x_min=min(X)
x_max=max(X)
x_w = np.linspace(x_min,x_max,2)
y_w = x_w*W[1]+W[0]
plt.scatter(X,y)
plt.plot(x_w,y_w,'r')
plt.show()
## 函数形式
def LR(X,y):
    ones=np.ones((X.shape[0],1))
    X_ones = np.hstack((ones,X))
    XT=X_ones.T                #求X转置
    XTX=np.dot(XT,X_ones)
    XTX_1=np.linalg.inv(XTX)
    XTX_1XT=np.dot(XTX_1,XT)
    W=np.dot(XTX_1XT,y)
    return W

2，线性回归

3，逻辑回归

第四章 决策树

决策树：内部结点节点对应属性；叶结点对应标签；分支对应属性值；

1，基本流程

2，属性划分原则

信息商：
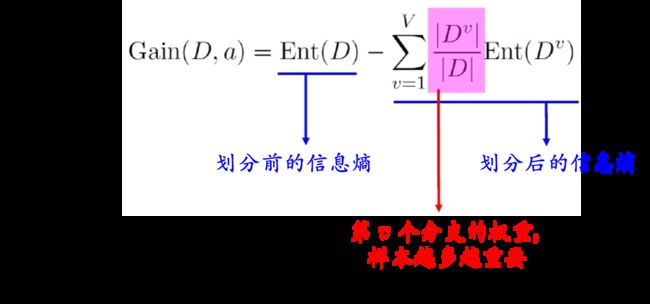
信息增益：在划分数据集之前和之后信息发生的变化。获得信息增益最高的属性就是最好的选择。

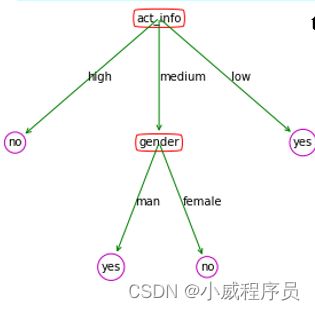
决策树的字典结构：
决策树={根节点属性：{}}
={根节点属性：{
分支1（内部结点）:{ },
分支2（叶子结点）:类别
}}

tree={}   #空决策树
tree=
 	{'act_info':
		{'high':'no',
		'medium':
			{'gender':
				{'man': 'yes',
				'female':'no'}
		},'low':'yes'}
}

# 一，决策树
## 1，读取西瓜集ex4.csv
from pandas import read_csv
df = read_csv("ex4.csv",header=None)
data = df.values
X = data[:,:-1]
y = data[:,-1]
names_chinese =['色泽','根蒂','敲声','纹理','脐部','触感']
names_english = ['color' , 'root', 'sound','texture' ,'navel','feeling']
label_chinese =['好瓜','坏瓜']
label_english = ['good', 'bad']
## 2，求信息商
import numpy as np
def calEntropy(y):
    classes = np.unique(y)
    ent = 0
    for c in classes:
        pc = len(y[y==c])/len(y)
        ent = ent-pc*np.log2(pc)
    return ent
## 3，求信息增益
def calInfoGain(X,y,index):
    ent_f = calEntropy(y)  #划分前的信息商
    ent_e = 0              #划分后的信息商
    for v in np.unique(X[:,index]):
        sub_y = y[X[:,index]==v]               # ？？？
        ent_e = ent_e + len(sub_y)/len(y)*calEntropy(sub_y)   # 对应公式累加得到划分后的信息商
    gain = ent_f - ent_e
    return gain
 ## 4,最优属性选择
 def getBestFeature(X,y):
    maxGain = 0
    label = 0
    for i in range(X.shape[1]):
        gain = calInfoGain(X,y,i)
        if gain>maxGain:
            maxGain = gain
            label = i
    return label
names_chinese[getBestFeature(X,y)]     # 输出 ‘纹理’

增益率：
利用信息增益对属性进行划分，对属性值数目较多的属性有所偏好，为了克服这个弊端，引入了增益率的概念。增益率计算公式如下：
$$Gai{n}_{r}atio(D,a)=\frac{Gain(D,a)}{IV(a)}$$
其中：$IV(a)$称为属性固有值，V越大，则$IV(a)$越大
$$IV(a)=-\sum _{v=1}^v\frac{|D^v|}{|D|}lo{g}_2\frac{|D^v|}{|D|}$$

3，剪枝处理

在决策树学习过程中，为了尽可能正确分类训练样本，可能划分的较多，有时会造成决策树分支过多，这时可能会因训练样本学得太好，以致于把训练集自身的特点当作所有数据都具有的一般性质导致过拟合。
决策树剪枝是对付过拟合的一种手段，通过主动去掉一些分支来降低过拟合的风险。

(1)预剪枝

(2)后剪枝

第五章 神经网络

感知机-单个神经元模型

单层感知机
感知机由两层神经元组成。

仅输出层称为M-P神经元，输入层不能称。线性变换：$z=w_1{x}_1+w_2{x}_2$
多层感知机-多层前馈神经网络
由输入层、隐藏层、输出层构成。
M-P神经元：隐藏层、输出层