LU分解
实验题目：LU分解
实验目的：掌握把一个矩阵进行LU分解算法；
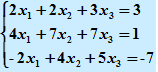实验内容及要求：LU分解法求解线性方程 。要求输入一个矩阵；显示输出L阵和U阵。其中L为下三角，U为上三角
代码
1
#include
"
iostream
"
2
using
namespace
std;
3
void
main()
4
{
5
int
i,j;
6
float
A[
3
][
4
]
=
{{
2
,
2
,
3
,
3
},{
4
,
7
,
7
,
1
},{
-
2
,
4
,
5
,
-
7
}},U[
3
][
3
]
=
{{
0
,
0
,
0
},{
0
,
0
,
0
},{
0
,
0
,
0
}},L[
3
][
3
]
=
{{
1
,
0
,
0
},{
0
,
1
,
0
},{
0
,
0
,
1
}},Y[
3
],X[
3
];
7
for
( i
=
0
;i
<
3
;i
++
)
8
for
( j
=
0
;j
<
3
;j
++
)
9
{
10
U[
0
][j]
=
A[
0
][j];
11
L[
1
][
0
]
=
A[
1
][
0
]
/
U[
0
][
0
];
12
L[
2
][
0
]
=
A[
2
][
0
]
/
U[
0
][
0
];
13
U[
1
][
1
]
=
A[
1
][
1
]
-
L[
1
][
0
]
*
U[
0
][
1
];
14
U[
1
][
2
]
=
A[
1
][
2
]
-
L[
1
][
0
]
*
U[
0
][
2
];
15
L[
2
][
1
]
=
(A[
2
][
1
]
-
L[
2
][
0
]
*
U[
0
][
1
])
/
U[
1
][
1
];
16
U[
2
][
2
]
=
A[
2
][
2
]
-
(L[
2
][
0
]
*
U[
0
][
2
]
+
L[
2
][
1
]
*
U[
1
][
2
]);
17
}
18
19
cout
<<
"
array L:
"
<<
endl;
20
for
( i
=
0
;i
<
3
;i
++
)
21
{
22
for
( j
=
0
; j
<
3
; j
++
)
23
{
24
if
(i
==
2
&&
j
==
0
) printf(
"
%.3lf
"
,L[i][j]);
25
else
printf(
"
%.3lf
"
,L[i][j]);
26
}
27
printf(
"
\n
"
);
28
}
29
30
31
32
cout
<<
"
array U:
"
<<
endl;
33
for
( i
=
0
;i
<
3
;i
++
)
34
{
35
for
( j
=
0
;j
<
3
;j
++
)
36
printf(
"
%.3lf
"
,U[i][j]);
37
printf(
"
\n
"
);
38
}
39
40
41
42
Y[
0
]
=
A[
0
][
3
];
43
Y[
1
]
=
A[
1
][
3
]
-
Y[
0
]
*
L[
1
][
0
];
44
Y[
2
]
=
A[
2
][
3
]
-
(L[
2
][
0
]
*
Y[
0
]
+
L[
2
][
1
]
*
Y[
1
]);
45
46
47
X[
2
]
=
Y[
2
]
/
U[
2
][
2
];
48
X[
1
]
=
(Y[
1
]
-
(U[
1
][
2
]
*
X[
2
]))
/
U[
1
][
1
];
49
X[
0
]
=
(Y[
0
]
-
(U[
0
][
1
]
*
X[
1
]
+
U[
0
][
2
]
*
X[
2
]))
/
U[
0
][
0
];
50
cout
<<
"
Result:
"
<<
endl;
51
52
for
(i
=
0
; i
<
3
; i
++
)
53
printf(
"
X%d=%.6lf\n
"
, i, X[i]);
54
55
56
57
}