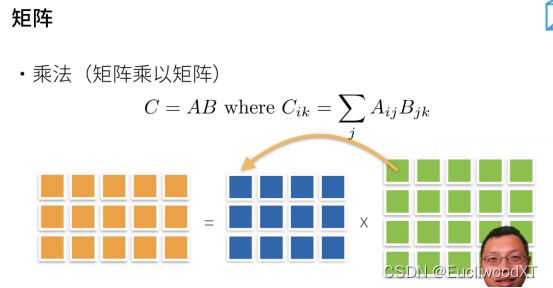
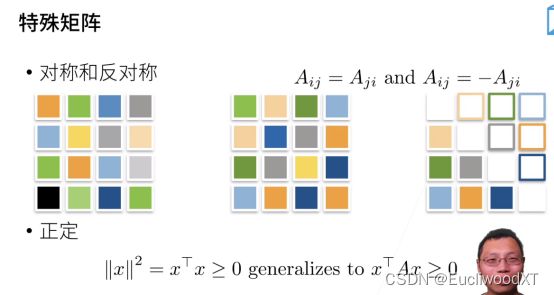
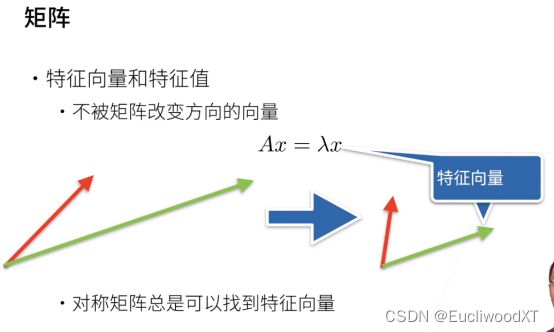
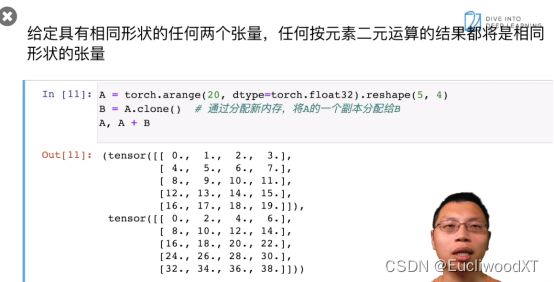
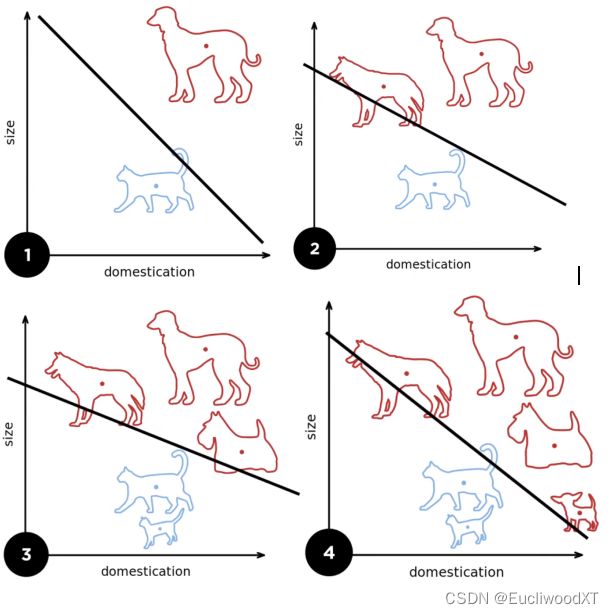
【深度学习】动手学深度学习PyTorch版笔记

1 前言

        看完前言！
        刚学深度学习那会看的是李沐老师的视频，同时做了些笔记，基本都是自己主观性比较强的笔记，而且也没看完，看了前面十几集后基本就是直接上实战，然后跳着看了。
        建议学习深度学习的同学直接去看视频跟李沐学AI。
        另外还推荐李宏毅老师的深度学习视频，不过他的视频我只看过部分，当时是结合李沐老师的视频看的，感觉很不错。看李沐老师的视频可能需要一些基础，而且老师讲的有些地方的确不太好理解（我是这样），我当时就是不懂了再去看李宏毅老师的对应部分内容，不过这不代表李沐老师的课程不行，整体感觉上我还是更喜欢了李沐老师的课程，我推荐的学习方法是看李沐老师的视频，然后不懂的自己再去查询。
        还有吴恩达的教程视频，不过他的我没看过，但最早大家都是看他的视频，这里给大家参考。
        当然还有实战推荐，B站Up霹雳吧啦Wz。若急于实战跑实验什么的，可以考虑直接看他的视频，或者先把李沐老师的前23个左右的视频看了再来看他的，毕竟有了概念实战才更好理解。
        全是主观推荐哈。笔记感觉大家也不用看，虽然有些写一些自己的理解，但也只是我自己的理解，没法保证笔记内容的100%正确性，不过大家想看看扩散下思维的话，我也会很高兴。
        总之，建议大家直接去看视频。

2 序章

2.1 课程安排

2.2 深度学习介绍

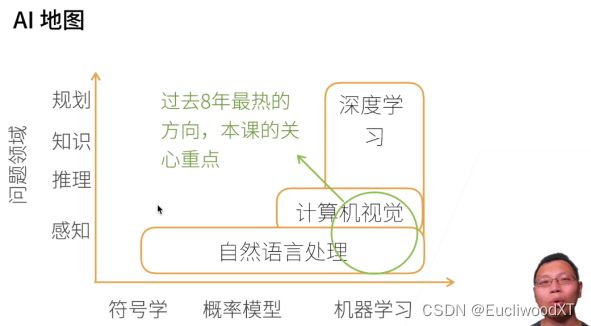
2.2.1 AI地图

PS：人几秒内反应的东西，就可以理解为感知。

2.2.2 应用

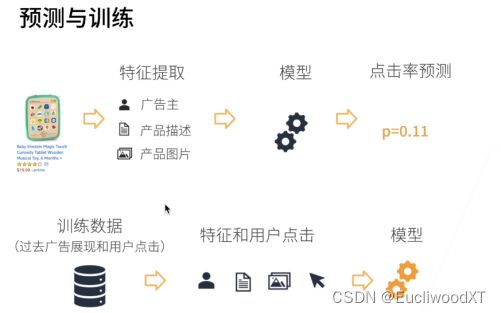
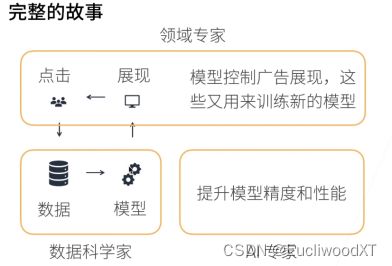
2.2.3 简单案例讲解

1. 领域专家：更关注应用，了解业务，也可以理解为需求的提出者。
2. 数据科学家：着手于数据与模型，训练调整模型。
3. AI专家：对模型进行更细微化的调整。

实际上吧，一般2和3是一体的，更甚123是一体的。

2.3.4 QA环节

Q：深度学习为什么这么有效，目前有定论吗？

A：深度学习目前还是黑盒，为什么有效还没有比较好的解释。在机器学习中，一些算法有较好的解释，但更为深入的内容也没有较好的解释。有效性是一回事，提出新模型有效，其原因我们可以简单解释，但人能不能理解其本质又是另一回事，这即是可解释性。“有效性”和“可解释性”要分开来看。更好的解释只能等科学的新进展。

3 安装

下面两句是修改后的可使用命令：

• conda create -n d2l-zh -y python=3.8 pip
• pip install jupyter d2l torch torchvision

PS：测试发现在新环境里下载包（pip）是直接下载到环境文件里。然后删除环境时这些包也删除了（占用空间没了）。

4 数据操作

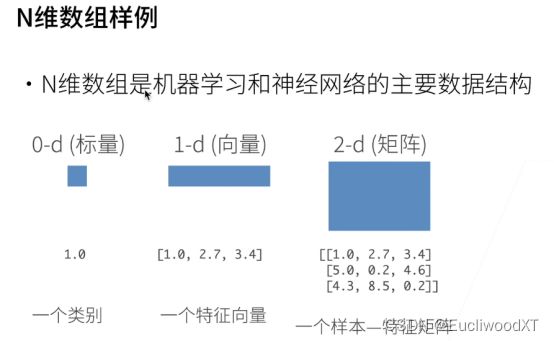
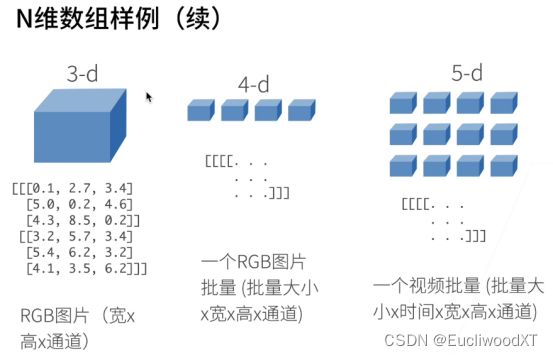
4.1 主要数据结构

4.2 创建数组

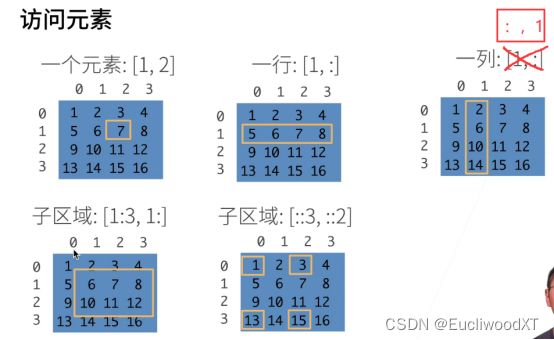
4.3 访问元素

4.4 操作实现

注意，下面2,3,4表示，2个3x4的矩阵，是三维。还要留意[]括号的层数，基本跟维数对应。

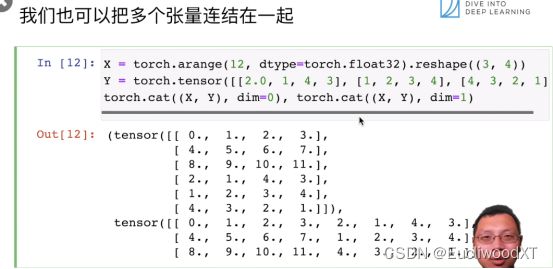
cat是合起来的意思，dim是维度，这里dim=0表示按0维合起来，即按行合起来；dim=1是按1维合起来，即按列合起来。

广播机制。相加的张量形状一样时，正常相加，但当不一样时就会触发广播机制。看图中所示3,1和1,2相加时触发广播机制，3,1和1,2都让自己扩为了3,2的样子然后再相加（以复制方式来扩，比对下结果是可以看出它们是如何复制的，这里就不说了）。

注意，这类虽然是最后一个元素，但二维张量中元素实际上是行，所以最后一个元素指最后一行。

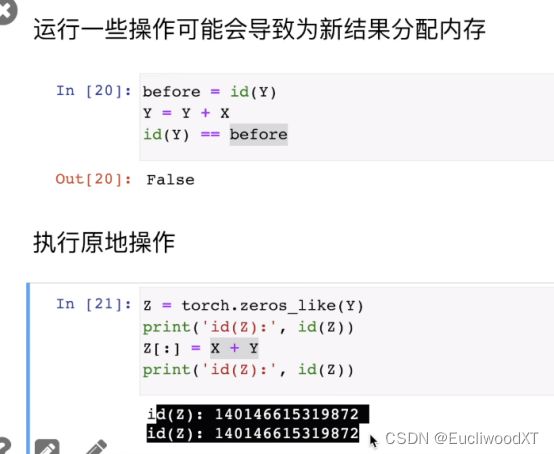
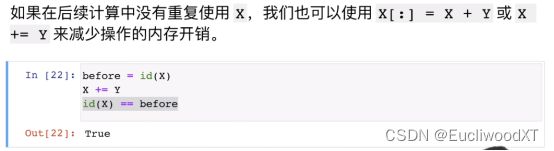
Id()获取一个对象的标识号，实际上就是内存的十进制标识。图中还附带了原地操作的方法。上部分的操作本质是创建了一个新Y，而下部分的操作时对Z进行赋值。下图也给了别的方法。

下图说的是类型问题，numpy和torch是两类张量，都可以用。其中下部分是说类型转换问题。后两个float和int是python的类型，而item那个老师说是numpy的浮点数，这里不懂为什么是numpy的。【？】

4.5 数据预处理

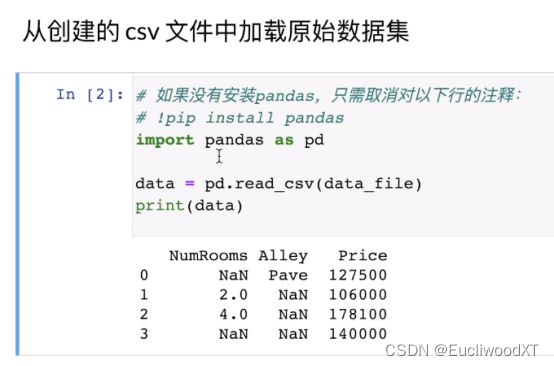
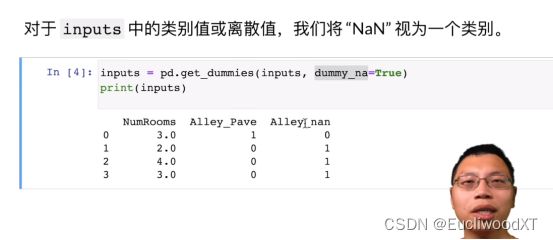
创建一个csv文件，然后将csv文件中的内容读取进来，将内容转成数值形式，这其中涉及到了“分类”，然后因其全为数值了，所以再将整个内容转成张量格式，方便我们后续操作。

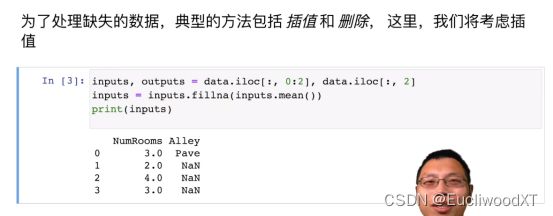
以上，将0和1列放入inputs中，将最后一列即2列，放入outputs里。iloc即indexlocal。fillna是将数据中NA部分填值，这类mean是inputs的均值，原先只有4和2，所以这里填3。

分类，使用get_dummies函数来进行分类，对inputs分类（这里是对Alley），dummy_na=true意味着将NA也看作一类。结果如上图可知，后面Alley变成了Alley_Pave和Alley_nan，这就是我们分的两个类。其中，下面对应的1和0是表示当前行对应的值是否是当前类的，1即是，0即否（对应上上图来看，很好理解）。

4.6 QA

Q：reshape和view的区别？

A：（自）torch的view()与reshape()方法都可以用来重塑tensor的shape，区别就是使用的条件不一样。view()方法只适用于满足连续性条件的tensor，并且该操作不会开辟新的内存空间，只是产生了对原存储空间的一个新别称和引用，返回值是视图。而reshape()方法的返回值既可以是视图，也可以是副本，当满足连续性条件时返回view，否则返回副本[ 此时等价于先调用contiguous()方法在使用view() ]。因此当不确能否使用view时，可以使用reshape。如果只是想简单地重塑一个tensor的shape，那么就是用reshape，但是如果需要考虑内存的开销而且要确保重塑后的tensor与之前的tensor共享存储空间，那就使用view()。

原文链接：PyTorch：view() 与 reshape() 区别详解_pytorch view reshape-CSDN博客

Q：针对数据处理感觉跟不上了，学些什么基础？

A：numpy。

Q：pytorch和numpy类似吗？

A：不类似。

Q：numpy中的ndarray与pytorch的tensor有什么区别？

A：数组与张量。实际上没有区别，一样，不过前者是计算机上的概念，后者是数学上的概念，不用纠结。

5 线性代数

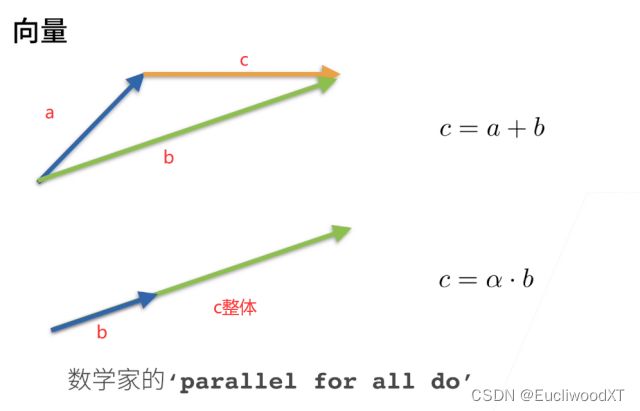
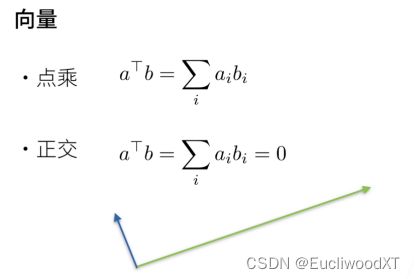
5.1 线性代数

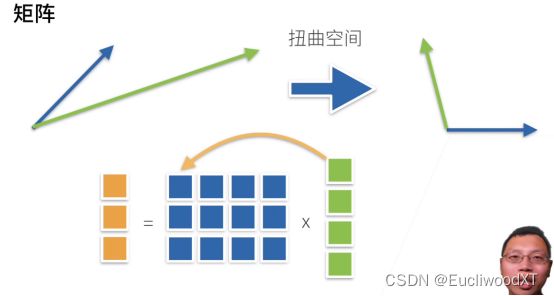
矩阵与向量相乘，本质是对空间的额扭曲，如上两个向量经过矩阵乘法变成了另外两个向量。

U和P都指代矩阵。

特征向量方向不会被改变，大小可以被改变。看公式，考研内容啊！

5.2 线性代数的实现

5.2.1 标量、数组、矩阵

5.2.2 矩阵转置

5.2.3 多维张量（3维）

5.2.4 矩阵计算

5.2.4.1 相加

5.2.4.2 哈达玛积（一般的点乘）

5.2.4.3 元素和、均值（某一维度进行、保持维度）

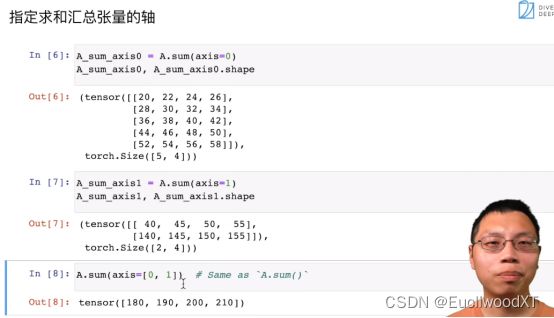
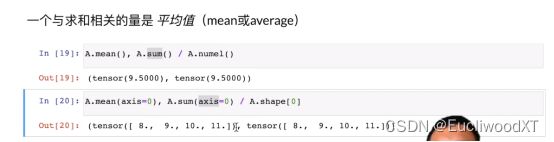
如图（上述两图），按照维度求和，axis是指定维度，注意维度从2,5,4来看分别为0,1,2，具体的求和效果看结果就行了，不难。

注意维度求和除以维度形状，因为前面的2,5,4是修改的，没修改前是二维的，所以这里0代表的维度是行，所以求和是行求和，然后shape[0]则代表的是行数。这个0维度为什么是行跟前面2,5,4是样的，比如2,5，那么就是2行5列，2是0维，5是1维。

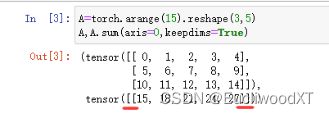
保持维度不变，可以用于广播机制，因为广播机制要求维度一样（形状不一样触发广播机制）。Keepdims=True来设置保持维度不变。代码是我测试的结果（因为无A原样），观察红线处，有两个括号，即代表着维度是二维，去看看前面的案例相加后维度直接降下去了（括号减少了），所以这就是保持维度不变的含义。

5.2.4.4 累加

因为缺少A本来的样子，所以我自己做了个。

5.2.4.5 点积（内积）

矩阵点积，向量矩阵点积就是正常的乘积计算，不是对应位置乘对应位置！向量的确是对应位置乘对应位置，但应该也是那种行乘列的形式。不过要注意在pytorch中一般点积都是行向量乘行向量，矩阵乘行向量，然后效果跟数学上线代里的计算一致。

上面那句话说的不太清楚，我自己测试的是：对应位置相乘再相加，A第一行点乘x，然后第二行，第三行，每次结果给一个值，参考我自己测试的结果。实际上跟正常矩阵与向量相乘是一致的。

计算过程与正常矩阵相乘一致。

5.2.4.6 L2、L1范数

5.2.4.7 L范数

5.3 按特定轴（维度）求和

就说一点吧，keepdims=true保持维度，那么那一维度会保留下来，数值会变成1，比如多行变一行这样。如果没有保持维度，那么这个数值直接就没了，比如2,5,4→2,4与2,5,4→2,1,4。这样对比来看。

6 矩阵计算

主要讲解了求导问题。

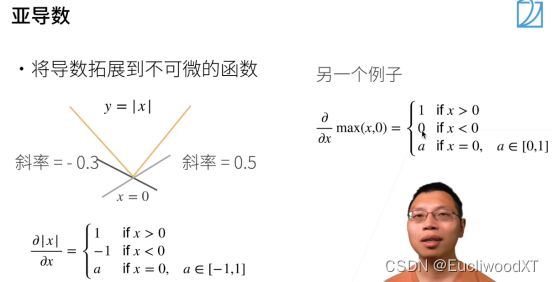
6.1 标量导数、亚导数

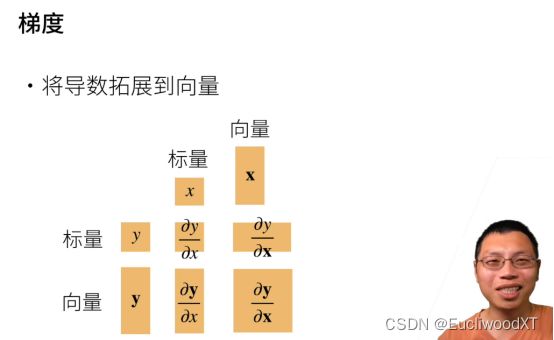
6.2 梯度

注意上面面积大小表示标量、向量、矩阵。

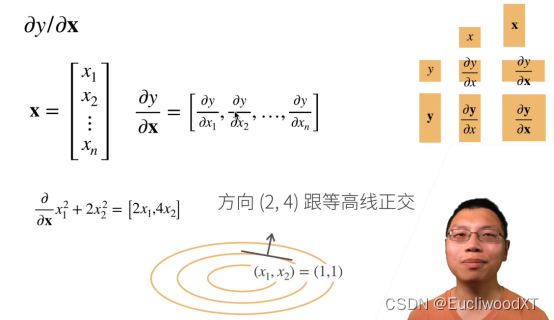
        这里，然后按照上述求导公式求导，这里x是向量，就变成了。梯度指向值增加变化最快的方向。
        在这里说明下，我认为只有一个自变量的函数，就是画出的函数图是二维图的那种，是没有梯度的概念的，只有导数，老师前面也是把导数和梯度区分开来了，所以对于这种函数没有梯度只有导数。导数指向使因变量增大的自变量变化方向。但导数本身还表示了高一维度中的一个方向。
        梯度是什么？我们求导所得向量就是梯度。其指向因变量值增大最快的方向。但是这个方向到底是什么方向？是自变量变化的方向。但是梯度本身还表示的是比自变量方向更高纬度的一个方向，这里设为“梯度表示的高纬度方向”。设z=f(x,y)，x、y是自变量，z是因变量。函数图形是三维图形，有一点(x,y,z)，它有无数个个三维方向，我们约束到某一方向，其满足：“这个方向是因变量z增大最快的方向”，那么这个方向就是“梯度表示的高纬度方向”。
        我认为梯度或导数都可以看成“各维度自变量方向+其方向上的因变量值变化强度”。以y=f(x)这种一个自变量函数为例，假设x1求导结果为3，那么只看这个3它则代表x1往正方向变化，y值增大，只用作自变量方向的话3这个值可以无视直接看作1，换言之求导结果可以直接看成是一个带有长度的能让因变量值增大的自变量的方向，这即是“+”的前半部分；后半部分说了因变量变化强度，即3这个值，有什么用呢？我们可以结合前半部分的方向和后半部分的强度值，在一个二维坐标系空间中“画”出一条二维方向（“导数表示的高纬度方向”），如何画？给你个点和斜率让你画线会画吗？。
        以z=f(x,y)为例，按老师的例子看，求导结果为（2,4），2和4分别代表了x或y往正方向变化可以使得z的值增大，它们关注的是2和4的1:2关系，值是多大无所谓，关键在比例上，然后两个方向结合形成的二维方向则是因变量x,y整合的方向（x，y同时变化就相当于整合两者的方向了），这个方向具有“z值增大速度最快”的属性。那么如何获得那个三维空间的方向呢，对每一维度的方向x,y分别“画”出其二维方向（z与x/y）（类似于y=f(x)），然后两条二维方向结合形成一条三维方向，这就是“梯度表示的高纬度方向”。
        至此可知，我们得到的结果梯度是一个多维向量，表示的是【使因变量增大的多维自变量变化方向的集合向量，每个维度的值表示的是这个维度上因变量的变化强度。整合起来看就是比函数图像低一维度的向量，向量方向是使因变量增大速度最快的多维自变量整合后的变化方向，长度越长因变量变化强度越大。另外别忘了还有，“梯度表示的高纬度方向”，就是函数图像中一点的方向。】
        导数更简单，就是个一维向量（也可以说标量吧...），然后表示的“高纬度方向”就是我们画的切线...
        通过导数、梯度的方向（自变量方向）所具有的特性，我们可以借此来实现梯度下降算法。第八课会讲梯度下降算法。
        梯度图：

是内积。内积就是两矩阵对应位置元素相乘再相加。||x||的平方，这里应该是2范数，一般没有在右下说明是几范数的话默认是2范数，所以这里是2范数的平方。

对y中每一元素进行向量x求导，之后每一个求导就变成后续的行向量了，整体就是矩阵了。

I是一个单位矩阵。A是矩阵。

这个沐神说了解一下就行，要关注维度增加的排列，比如最后遮住的那个是m,l,k,n，k和n来自矩阵X，但k和n的顺序相比矩阵X是相反的。矩阵的求导这里没有展开，后续考虑学一下。

7 自动求导

7.1 自动求导

7.1.1 向量链式法则（求导）

注意第二个，(1,k)(k,n)这两个相乘还是会变成(1,k)。第三个同理。这里是说明计算过程以及计算过程中形状的变化。

这里有I，是单位矩阵，但我感觉这里写成1也没问题，求导结果就该为1，而且I与1参与计算的最终结果也一致。（单位矩阵或1 乘矩阵A结果还是A）

7.1.2 自动求导

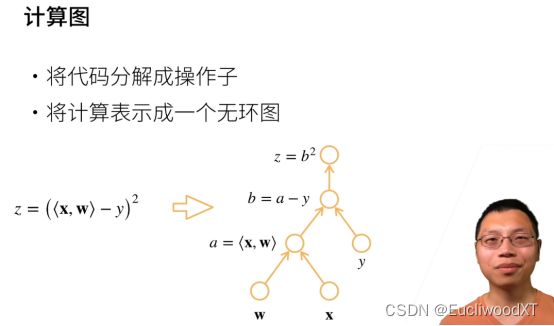
7.1.3 计算图（自动求导的原理）

7.1.3.1 图解

7.1.3.2 显式构造

显式构造，先定义计算方法（如公式、函数）不给输入值，然后再取值代入。

7.1.3.3 隐式构造

隐式构造，先给值，然后再给公式。我的理解是拿到两个赋值的变量，然后直接写计算过程。应该是这样吧【？】

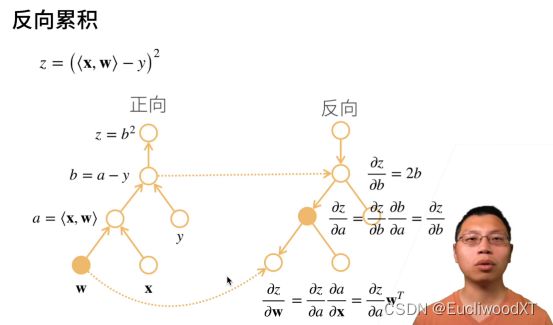
7.1.3.4 自动求导两种模式

求值的顺序不同。

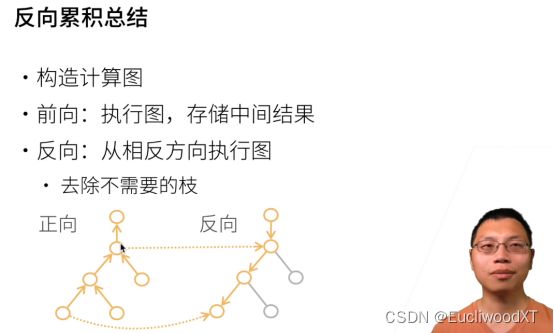
反向过程中，需要正向的中间结果拿来用。

注意反向过程中有些不需要的枝就不需要计算导数了，且使用前向的存储结果。前向全部节点计算。

深度神经网络特别耗GPU资源，祸源就在“需要存储正向的所有中间结果”，求梯度的时候需要把前面的结果都存下来。

最后两条是正向累积的属性。反向→双O(n)，正向→O(n)，O(1)。

正反关系还是有点迷。【？】

我的理解正向就是一次正向，不存储中间结果，每次计算从头。而反向呢，则是先一次正向，然后后续计算都是靠反向。这是我的猜测。

7.2 自动求导实现

7.2.1 求导演示

后面的grad_fn=<····>是因为隐式构造了计算图，告诉我们有个求梯度的函数存在这里。

这里为什么是跟4*x对比，可以把前面xtx看成L2范数的平方，然后结合前面“梯度”章节里的求导表，带入整体公式，就可以得到求导结果为4*x了。

Backward()→反向传播函数。

7.2.2 sum求导

为什么是全1呢，sum后就向量x与全1向量的内积，自己动手算算。

7.2.3 非标量求导

标量问题。这里的y可能是个矩阵（x*x的计算结果），而我们一般只对标量进行求导（y的结果是标量），所以一般会sum求和再求导（sum后就成标量了，相加成一个数了）。后续sum这个问题还会讲。

7.2.4 某些计算移出计算图

如字面意思，移动到计算图之外，可以理解为把某些内容变为常数。如代码所示，y是x的函数，u是y通过detach转为了常数，则z是一个常数乘x。那么z sum的x求导就为u。但不不影响y本身，y本身还是x的函数，我们还可以通过y进行求导（下部分代码）。

7.2.5 构建函数计算图，涉及到控制流

        这里才看出点东西，前面我们写y=xxxx，这些实际上也构建了计算图，只不过这里讲函数计算图的构建，说得更明白了点。先讲了计算图是先构建的，比如f()函数，本身会存储中间内容构造计算图，然后反向执行一次就得到我们的矩阵（不明白为什么是矩阵）了。这个过程是隐式构建，按老师说法，隐式构建的好处是对控制流做得更好些，但速度会慢些。
        这里说做得更好些，我的理解是：如代码中有b=b*2那么循环多次时构建的计算图能准确区分出“变量”与“常数”，图中函数f()的结果肯定是一个a变量乘一个常数，这就做了准确的区分。
        Size=()表示a是一个标量。后面a.grad==d/a是对结果的验证，就是验证f()返回的是一个a变量乘常数（可能一个，可能多个，整体可看成一个A，即aA），又因为a是标量不用sum所以直接求导即可。结果为ture，可知d=aA。
        从代码看为什么是aA：倒着看，兄弟，d=f(a)=c,而c要么是b要么是b*100，而b要么是a*2，要么是a乘以好多个2，综上得到d最终结果都是a乘以几个实数，那这个实数用A表示，则整体上d=f(a)=Aa。（来自弹幕）

8 线性回归+基础优化算法

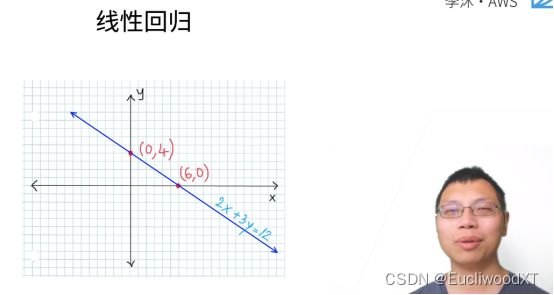
8.1 线性回归

介绍了线性模型，以及这个模型的损失函数，并求解了其最优解。这个算是最简单的模型了，就这个有最优解，其他后续学习的模型都不会再有最优解了。

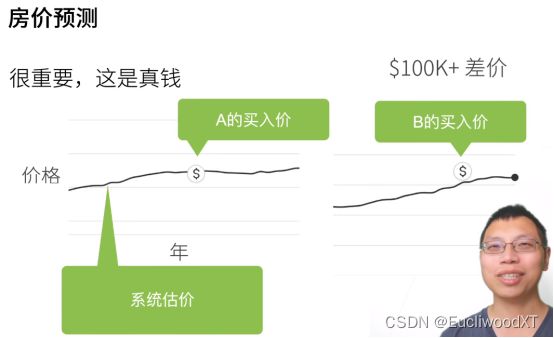
8.1.1 美国买房案例

A低于系统估价，很好。B高于系统估价10w美元，李沐现身说法。

8.1.2 线性模型

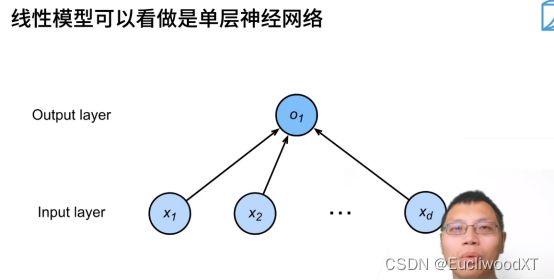
8.1.3 线性模型与单层神经网络

箭头可看为权重w。这里没画偏差。
为什么叫单层神经网络？是因为带权重的层就一层，我们把权重跟输入层放在一起，我们可把输出层不当作层。

8.1.4 训练数据

1-n个x是列向量，大是一个矩阵。1-n个x按列排好，然后转置，那么大X对应的一行就是一个样本（每一行就是一个小x，第一行就是x1）。
1-n个y是数值，y就是一个列向量。

8.1.5 参数学习（损失函数，最小化求解参数）

        损失训练即损失函数，用于计算预测值与真实值的差异。
        1/2是损失函数自带，1/n是求均值，yi是真实值标量，是两向量内积，w是权重向量里面有多个小w标量，b是标量偏差。
        实际可看得出，中间平方里的部分可看成yi-（+b），括号里面就是线性模型。
        目标：找到一个w和一个b使得公式得出的值最小。下面公式表达的就是这含义，最终获取两个参数。

8.1.6 显式解（最优解）

求解线性模型损失函数的最优解。

        如何把偏差加入权重：在大X最右边加入一列全1，然后在权重向量w下加上偏差值b；这样一来内积时，长度就对应得上。
        凸函数就是向下凸的函数，就像个碗，有个公式来判断，以前学过，还不懂就百度。
        因为是线性模型，所以损失函数是凸函数，所以最优解是满足下面偏导等于0的公式，求这个公式就可以得到最优解了。最后求w*那个应该是线代里的求法，我已经忘完了....
        我对最优解满足偏导等于0的理解：因为是凸函数，所以通过偏导等于0可以求出最小值，即图形上的最低点。

8.1.7 总结

8.2 基础优化方法

当一个模型没有显式解时，就通过优化方法来求得最接近最优解的解。

8.2.1 梯度下降

这里讲得很清楚，看“马同学”的回答：梯度下降。

        wt是当前时刻的w，wt-1是上一个时刻的w。η是一个标量。求导是损失函数关于wt-1处的梯度。
        图中外层是大值，内层是小值。梯度是增加最快的方向，所以负梯度就是图中箭头的方向。η是学习率即步长，表示我们沿着方向走多远，可以理解为图中箭头的长度，或者说“修正长度”更合适。综合得，公式中wt-1后面部分的整体（不包括wt-1）可以看成图中箭头，η是长度，而求导公式和负号是方向。
        比喻的话就是，从最外层高山往下走，每次都走最陡的路线。

8.2.2 学习率选择

8.2.3 小批量随机梯度下降

梯度计算复杂度跟样本个数线性相关。批量大小越大结果越接近真实情况。

8.2.4 批量大小选择

8.2.5 总结

8.3 线性回归的从零开始实现

8.3.1 数据准备

X是个矩阵。0是平均数，1是标准差（方差），num_examples是样本数（行数），len(w)是列数。
内积权值w，加偏差值b。
加噪声值。
返回X，把y作为列向量返回。
真实值w、b。
返回特征（X）和标注（y）。freatures中样本数（行数）与labels数一致。

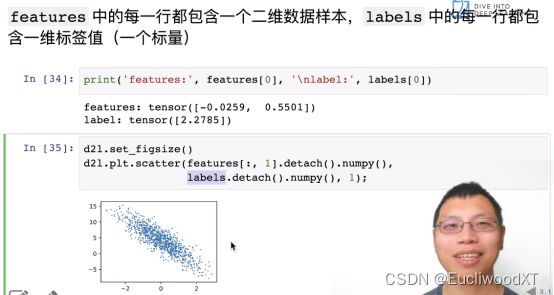
8.3.2 看了下features和labels的关系

图像横坐标是X第一列，纵坐标是y。

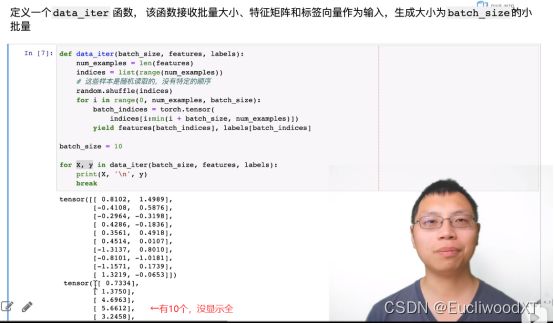
8.3.3 定义批量输出函数

len获取特征长度。
range这么多个数，值是0到n-1，再转list得indices，这是生成的下标。
Random.shuffle打算下标顺序。
for→从0开始到num_examples，每次步长batch_size。
随机获取一定数量的下标放到batch_indices中。最后一次返回的数量可能会比前面少，因为min的使用。
yield可以理解为迭代版本的return，batch_indices中有多个下标，它会一直返回features和labels直到batch_indices中的下标都返回完。
注意最后的break，所以只输出一次，输出了10组features和labels。

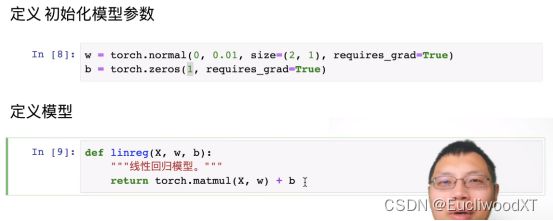
8.3.4 初始化模型参数、定义模型

这里matmul要自己去实验下，看看是如何计算的。

8.3.5 定义损失函数、优化算法

        损失函数那里没有去均值。y是向量，reshape是防止一个列向量一个行向量相减的情况。平方是向量平方，就相当于相减后的向量自身元素的平方和。
        With torch.no_grad()的意思是不计算梯度。这里是更新，梯度已经存储了（参考自动求导），所以直接拿梯度来用而不用计算。
        param就是参数包含w、b。Lr是学习率。param.grad是梯度，这里除以batch_size是因为损失函数那里没有除，就算加上边，也是个常量，求梯度并不影响“/batch_size”所以在上边加上结果也跟我们在上边不加在下边加效果一样。这里就是梯度下降那个公式。梯度的计算会默认累加，所以计算完梯度别忘清零，为下次准备。
        sgd函数这里传入的是参数集，修改直接反应到集合中，可以理解为指针，所以没有返回值。

8.3.6 训练过程

        学习率、整体循环3次、网络设置为线性模型（自己定义的函数）、损失函数设置为我们自己定义的。这个时候X和y原始数据已经准备好了（第一步的时候）。
        sgd中第三个参数不一定对，正如前面说的最后一批次长度不一定是batch_size，可能会少一点，那么这里除它就有误差了。
        这里训练是让损失函数值越来越小，也就是让w和b越来越接近最开始设置的true值。前面设置了一些噪声，应该是为了防止w和b学习得太完美，用来展示的（猜测）。

8.3.7 比较真实值

最后老师修改了学习率再学习一次，但要把w重新初始化一次，说是不按照上一次梯度来。这里的意思应该是修改w的随机值，如果和上一次值一样，那么梯度下降时，计算的梯度会和上一次的梯度一样，然后这样可能结果变化不明显吧，所以给修改了下w。

8.3.8 总结

        取一个X矩阵，一行是一个样本，这个X矩阵作为featrues。输入X到线性模型中，计算出labels，不过输出前加入了一些噪声，最终输出labels（这里加入噪声不太清楚是为什么）。在输入到线性模型计算时，我们设置了w和b，这是真实值，也是我们最想让结果接近的值。
        然后定义分批函数，定义w和b参数（随机设，我们后续训练不断调整的参数），线性模型，损失函数、梯度下降函数。
        进行训练，最外层是整体训练次数，内部循环进行多批次训练，把定义的w和b输入线性模型，计算出labels和我们原始labels做损失函数，然后使用梯度下降函数最小化损失值，来调整w和b，为了使计算出的labels越来越接近原始labels。每次最外层训练比对一次当前w和b经过线性模型计算所得labels与原始labels的损失值查看。
        最终用得到的w和b和真实w、b进行差值比对。

        另外，开始你就加入了噪声，人家怎么学都不会跟真实值w、b一样啊。所以我前面猜测加噪声就是为了让最终调整得到了w、b与真实值有误差。
        我的理解是，通过输入freatures与真实（原始）labels，来让所得labels与真实labels越来越接近，而接近就是通过不断调整w和b来实现的，所以训练的最后，网络会得到一些比较好的参数，这些参数可以实现输出的labels与真实labels极为相近。

8.4 线性回归的简洁实现

8.4.1 数据准备

多了import data那行。

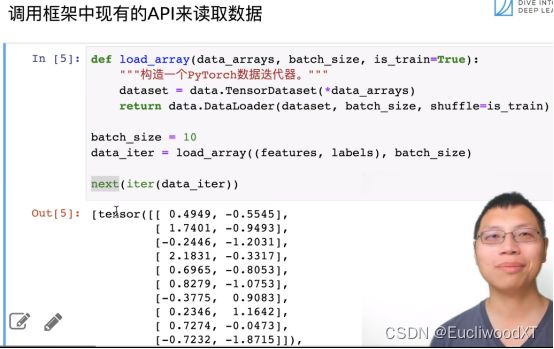
8.4.2 调用API分批数据

iter是转成python的iter。然后next一次读取一次，一次10个。

8.4.3 使用模型层、初始化模型参数

        Sequential是一个容器，可以理解为一个list of layers（多层）。Linear就是线性模型，两个参数是输入维度、输出维度（我们输入两个，输出一个）。
        通过net[0]访问到第一层，即我们的线性模型，weight就是权重w，data就是值，normal就是使用正态分布替换data的值。bias是偏差，fill给设置为0。

8.4.4 使用均方误差API、实例化SGD函数

SGD传入我们的参数（包括w、b），学习率。

8.4.5 训练

9 Softmax回归+损失函数+图片分类数据集

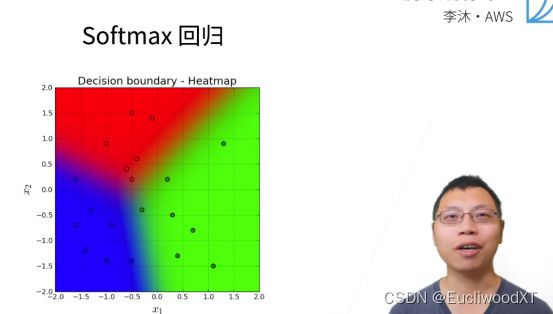
9.1 Softmax回归

9.1.1 回归不是归回

虽然是回归，但实际是分类问题。

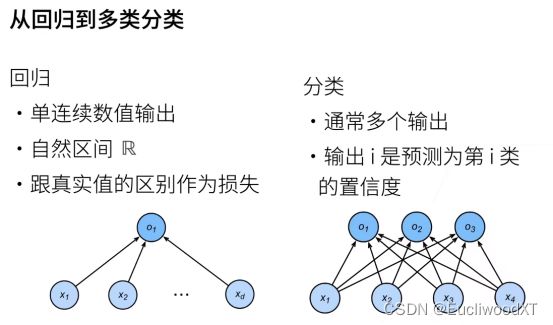
9.1.2 回归与分类的区别

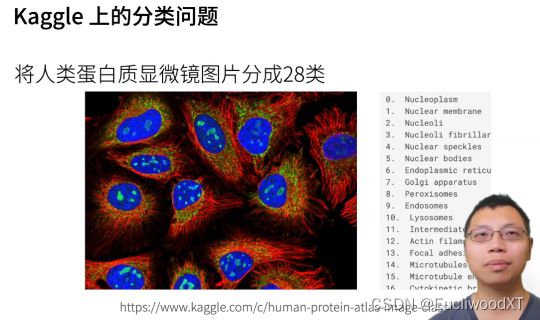
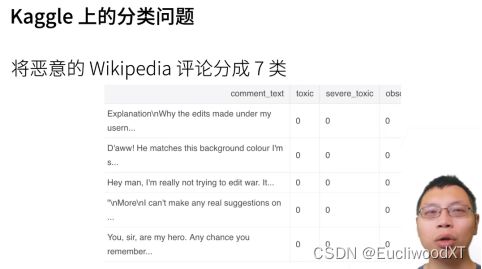
9.1.3 分类举例

9.1.4 从回归到分类，图解

从单输出变为多输出，输出的个数是类别个数。

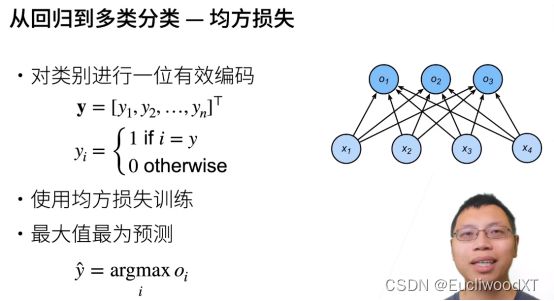
9.1.5 onehot编码

        y是一个标号，一个长为n的向量，n是类别个数，在这个向量中有一个属于自己的位置（通常自己是第几类，就是第几个位置），那么自己的这个位置为1，其他位置为0。整体看就是n个向量（n个类别）各不相同，每个向量有一个位置为1，其他位置为0。这就是One-hot编码，就是那种多行，每一行只有一个1其他都是0那种。
        i=y的意思是向量中这个i位置表示的类别与当前这个向量表示的类别一致，所以我们置其为1。
        最后从所有oi（一个oi一个值，每个oi表示一个类别，每个都有一个属于自己的下标）中找出类别预测输出最大的那一个，然后输出其下标i作为结果。i就是一个标号，第几个类别的意思。

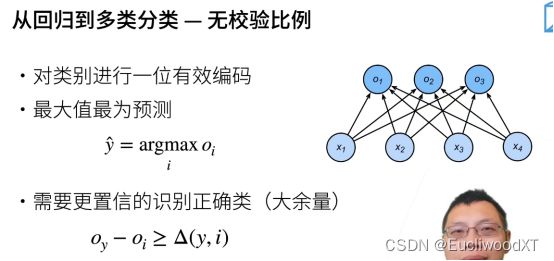
9.1.6 我们对结果的关注点

        分类问题我们不关心最终O实际的值，而关心分类是否正确，即O之间值的大小关系，所以我们一般让正确类Oy远远大于大于非正确类Oi，设一个阈值△（y,i），写成数学公式就是上述那个。
        虽然我们只关心相对值，但如果值被规定到一定区间是可以方便我们的，所以就有了后续操作。↓

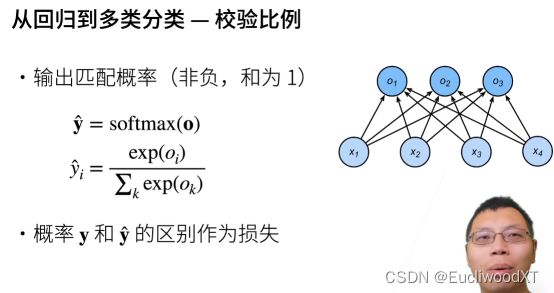
9.1.7 输出结果概率化（Softmax函数）

        softmax作用在O上得到的，是一个长为n的向量，其中每个元素非负，且和为1（注意图中加粗意为向量）。
        的公式是具体每个oi是如何在softmax里进行计算的。oi进行exp（e指数）操作，可以让值变为非零值，然后对所有oi进行exp操作再相加，一比，就进行了归一化，实现了“非负，和为1”。
        然后对真实O也进行概率化得y，就比如onehot，元素一个为1其他为0，和“非负，和为1”一致。接着区别作为损失。

9.1.8 交叉熵损失函数

        这里的例子，是对一个样本进行损失计算，实际中是多个样本，后面会讲。
        中间公式的简写，是因为真实y是0和1组成，只有一个元素是1，所以相加那里只要一个y位置的即可，这个位置就是值1的位置，也是代表当前类的位置。这个很重要，这里y输入onehot编码，针对的是一个样本预测的计算，得到简化公式后，可知我们只需要关注1的下标位置即可，即真实标签，或说真实类别，后面会讲到，然后在多个样本的时候，我们就用简化公式，这样一来就不看onehot编码了，只看真实标签（下标）。有什么好处呢，onehot是一行，一个样本需要一个，多个样本就成矩阵了，但是只要真实标签的话，多个样本形成的就是一个向量，方便计算。后面会有再说。
        最后的公式是求导，得梯度。

9.1.9 总结

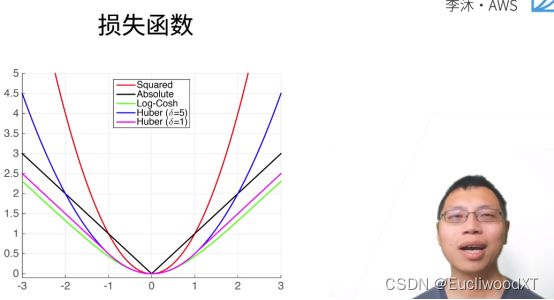
9.2 损失函数

        介绍三个常用的损失函数。

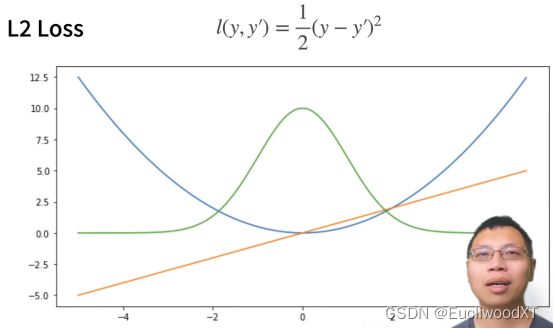
9.2.1 L2 Loss（均方损失函数）

        对比之前我们的均方损失函数，可知，我们之前对向量处理，所以最后是对每个损失值相加再取均值了。
        y→真实值，y’→预测值。
        蓝色曲线：y=0，y’作自变量。
        绿色曲线：似然函数....说是1的-l次方。
        橙色曲线：损失函数的梯度。

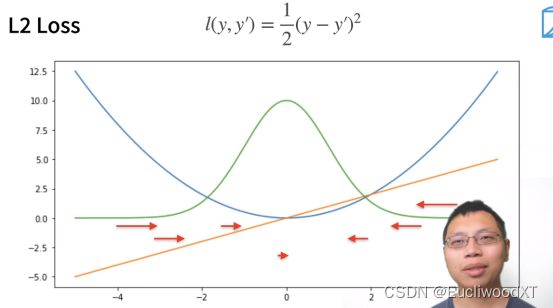
        红色箭头是梯度取反方向（损失值按箭头方向走减小），针对的是蓝色曲线，从曲线可看到与真实值y=0越接近，损失值的变化越慢，梯度的长度就越小，这跟我们之前说的梯度长度表示的内容一致（回忆复习下）。
        优点：越靠近真实值梯度越小，方便调整我们的参数。
        缺点：如果离真实值太远，梯度就会太大了，而我不一定想要那么大的梯度来更新我的参数。

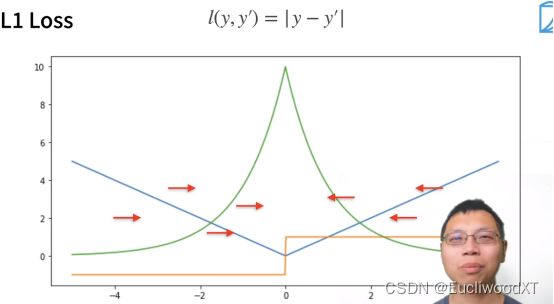
9.2.2 L1 Loss

        y→真实值，y’→预测值。
        蓝色曲线：y=0，y’作自变量。
        绿色曲线：似然函数....说是1的-l次方。
        橙色曲线：损失函数的梯度。
        特点：当你的预测值跟真实值相差比较远时，无论多远，梯度都是常数，这样对权重更新时步长也不会特别大。
        优点：这个会带来很多稳定性上的好处。
        缺点：0点处不可导（跟y有关，这里y是0），且梯度再0点处过渡不平滑，当预测值与真实值靠得比较近时，即在我们优化到末期时，这里就可能不稳定了。

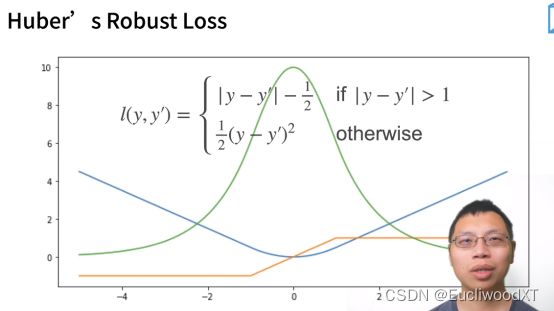
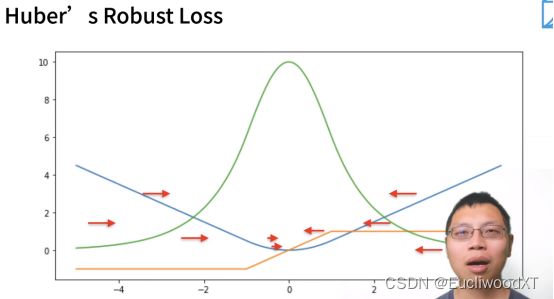
9.2.3 Huber’s Robust Loss

        y→真实值，y’→预测值。
        蓝色曲线：y=0，y’作自变量。
        绿色曲线：似然函数....说是1的-l次方。
        橙色曲线：损失函数的梯度。
        特点：结合了L1、L2损失函数的优点。

9.3 图片分类数据集

9.3.1 导入包

        Torchvision库：pytorch对于计算机视觉模型实现的库。
        最后一句：使用svg显图片，清晰度高点。

9.3.2 下载Fashion-MNIST数据集

        Root：数据所在路径。Train：表示是训练数据集还是测试数据集。Transform：转换类型。Download：是否下载的意思（若已下载好了，则False）。
        Mnist_train[0][0].shape：第一张图的shape信息。可知为1通道，长28，宽28。（[0][0]含义：数据由图片和标签组成，第一个下标，表第几个数据，第二个下标，0表图片，1表标签。）
        也可以提前下载，并不一定非要在pytorch中下载。

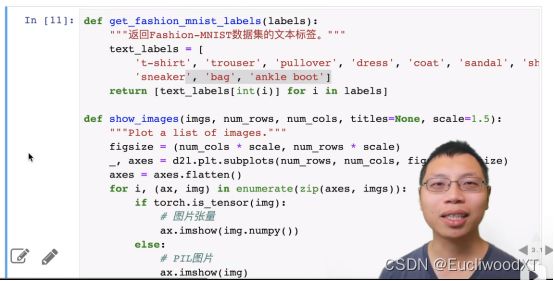
9.3.3 显示数据集-图片与标签

        2→两行，9→9列。y中是数值标号。

9.3.4 测试读取小批量数据所需时间

        timer测试速度。for循环是扫一遍数据，看看需要多长时间。
        一般情况读取数据的速度要比训练速度快些，这样才好。

9.3.5 定义一个整体函数---下载数据集并读入内存

        注意加入了resize功能。关于trans为什么加了[]，为什么trans使用了insert以及后面的compose，实际上是串联操作，具体看（https://blog.csdn.net/u013925378/article/details/103363232/）。

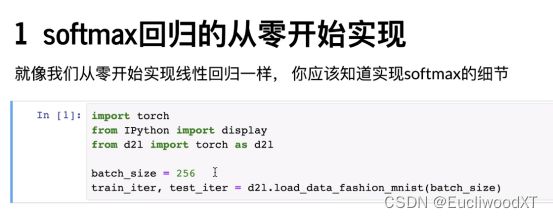
9.4 softmax回归的从零开始实现

前言---流程：

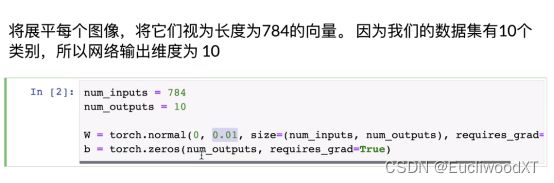
1. 假设，一张图像为一个样本，图像大小为3x3。图像分类类别有10个。
2. X为2维矩阵，代表总样本。一行为一幅图像，有9列（像素个数）。
3. w为2维矩阵，代表总权重。一行为一个权重（向量），有9行（像素个数），有10列（分类数）。
4. X与w进行内积处理，再加偏移值（实现回归模型）。一个图像形成一个长度为10的向量。最终为样本个数行，10列（分类数）的矩阵。
5. 对生成的这个矩阵进行softmax处理，每行为单位，实现整体数值概率化，行中每个值非负且总和为1。
6. 目前，我们手里的矩阵就是模型给我们的预测结果，一行是一个样本的预测，10列代表10个类别的预测值，越大的就是越可能归属的类别。
7. 后续损失函数，优化，精度计算等在笔记里看吧，前面6条捋清楚更好理解笔记。

9.4.1 读取数据

9.4.2 设置参数

        w（权重）。normal前面讲过，0均值，0.01方差，784行，10列，requires_grad=True（需要求梯度）。
        B（偏移值）。长为10的向量。

9.4.3 softmax实现

9.4.3.1 演示，矩阵行元素求和

        按0维（行），1维（列）求和。

9.4.3.2 softmax实现（对样本处理）

        弹幕：（每一行 是一个样本，列是其特征！sum(1,keepdim=True) 将所有的列进行压缩，求和成一列。）
        使用exp对每个元素计算，然后按1维求和，即每行累加为一个值。然后计算比值，每行去除以这行累加后的值（或者说这行每个值去除以）。
        弹幕：（善用广播机制可以避免循环，全部使用矩阵的运算完成。）

        2行5列的矩阵，结果还是2行5列的矩阵。
        弹幕：（在这里传入的不应该是y吗）（是的，这里只是做一个演示，方便看到softmax函数是怎么工作的）

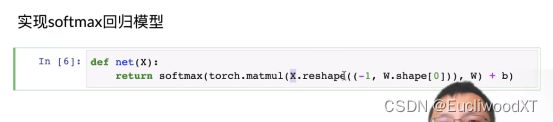
9.4.4 实现softmax回归模型

        我们需要的是一个“批量大小（行）”乘以“输入维数（列）”的矩阵。所以要reshape一下，-1是让pytorch自己算一下结果为批量大小，W.shape[0]是784（权重个数，一个权重是一个行向量，与图像像素数值一样）
        弹幕：（这里的reshape为什么是reshape(())，双层括号呀）（（其实不双层也可以），不过reshape里有很多参数值，第一个参数值是它的shape，传进去的是一个代表着维度的元组。（不知有没有讲清楚））
        这里我要详细说下。一张图像作为输入，是X的一行，列有784，则是图像的784个像素值。然后权重W行784，一行一个权重向量，所以相当于一个像素需要一个权重，然后权重是个向量嘛，里面是10个意味10分类。最终相乘后，有多少张图片就得多少个向量，每个向量含有10个值，每个值是图像分别对权重向量的每个值计算所得，自己想想矩阵相乘就知道了。

9.4.5 交叉熵损失函数

9.4.5.1 演示，特殊索引

        y是一个长度为2的向量，表示两个真实的标号。一个输入样本对应一个真实标号，标号是表明这个样本本应该属于什么类别。
        Y_hat是预测值，两个样本在三类中的预测值，三个值是一个样本在三个类别中的概率。
        Y_hat[[0,1],y]意思：y_hat[0,y[0]]、y_hat[1,y[1]]，即y_hat,[0,0]、y_hat[1,2]，再或者y_hat[[行],[列]]把每个都拿出来。在干什么：从预测值中拿出真实标号位置的值。

9.4.5.2 实现交叉熵损失函数

        多个样本计算，前面一个样本计算时提到过。
        Y_hat是预测（一行是一个输入图像的预测），y是真实标号（就是下标，就相当于是onehot里1值的下标，表示的是每个样本（图像）应该属于哪一类，样本预测值里那个下标位置的值才是我们的关注点）。
        Range(len(y_hat))生成一个0到y_hat长度-1的向量，共y_hat长度个数。
        这里y_hat就是锁定列，对每行进行数值提取。
        这里只针对y标号就行，具体看前面讲的交叉熵损失函数中间的公式，还是有些区别的，好像我们这里预测值维度高了一维，前面公式y实际上是onehot编码但针对的是一个样本，而中间公式进行了简化变形，所以是一个样本的简化，到这里就是应用到多个样本上，所以每个样本只需要关注自己的真实标号（下标）即可。

9.4.6 预测精度计算

        y是元素（向量， 值是下标），注意。shape→维度，shape[1]列数。
        如果是二维矩阵，且列数大于一。将y_hat中每一行(axis=1，按列方向走，感觉结果可看成一个列向量)中最大值的下标赋值给y_hat，相当于样本获得自己预测的分类结果。
        然后将y_hat数据类型转换成跟y同类型（因为他们可能不同类型，y一般为整型），再与y进行比较，每个预测值里最大值的下标与真实类别下标比对，看看预测的对不对，得bool结果，赋值给cmp。
        再转成y类型，求和。因为true为1，所以值就是我们输入图像中，正确预测的图像个数。
        和值比上y的长度（y的长度跟图像个数一致），即预测正确个数/总个数。

        Net.eval()，不再计算梯度
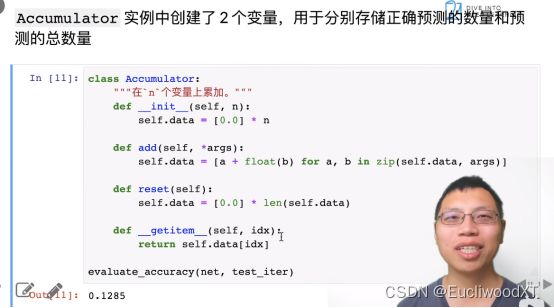
        add是累加的意思，相当于按批次遍历，把每一批次正确预测样本个数累加，批次总样本个数累加，最终得到的就是“所有样本中正确预测的个数”和“所有样本的个数”。
        最后，比值。

        很简单，难在我不懂python语法。就相当于C++里的类，实现一个函数来累加，实现方法有很多种，知道什么意思就行了，因为这里的实现还挺要python语法知识的。

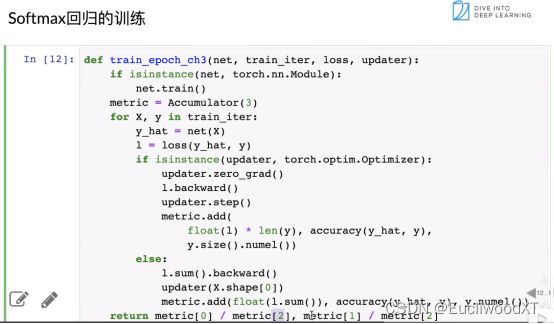
9.4.7 Softmax回归的训练

        如果是torch.nn.Module实现的话，开启train（训练模式）能计算梯度。
        定义迭代器，长度为3。
        遍历数据开始计算。
        计算y_hat（预测值），计算损失值。
        如果优化算法是torch.optim.Optimizer（这里不太懂，好像意思是用的跟之前的一样的话），梯度置零（防累加），计算梯度，参数自更新（优化）累加器累加（第一个参数没细讲，好像反映的是误差）。
        否则如果是自己来实现优化算法。求和，梯度，更新，累加。
        注意：优化算法updater在后面有实现。

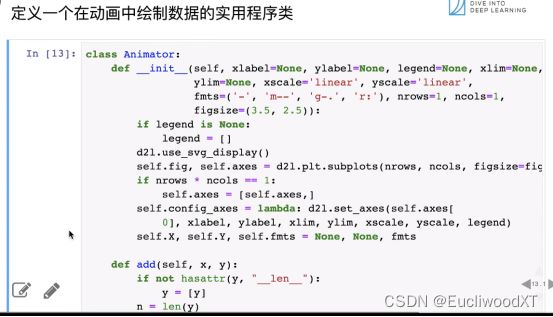
9.4.8 可视化代码（可以无视）

        数据可视化，可以无视。

9.4.9 训练函数

        第一个可视化无视。
        For来设置整体训练次数。
        训练返回误差、精度。
        测试返回误差、精度。
        可视化显示误差、精度。

9.4.10 优化函数（SGD）

        Sgd老朋友，梯度下降算法。

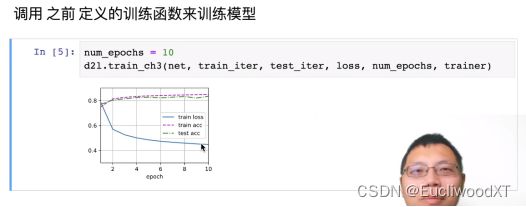
9.4.11 训练可视化展示

        训练损失、训练精度、测试精度。

9.4.12 图像分类预测展示

9.5 softmax的简洁实现

9.5.1 数据准备

9.5.2 网络准备

        nn.Flatten()是只保留2个维度。自实现里有256x28x28,3是批次数量，28是宽高，reshape成了256x784。这里保留2个维度就是做这个处理的。
        Nn.Linear（784,10），线性模型，784是输入，10是输出。线性回归简洁实现有讲。
        Sequential是一个构造器。构造网络。也可以理解为层，前线性回归简洁实现。
        Init_weights是用来生成权重的。
        m是model。看apply里是没有输入m参数的，所以感觉这个m就是net本身，是用于在函数中进行一些控制的。

9.5.3 损失函数、优化算法准备

9.5.4 训练

10 多层感知机+代码实现

10.1 感知机

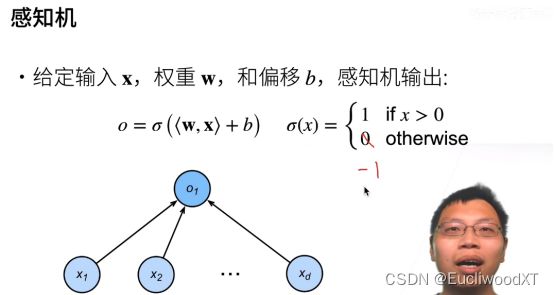
10.1.1 单层感知机

        可以理解为相比之前学的，加了个激活函数，变成了二分类问题。这里0和-1都可以，划掉只是举例可以。
        另外，这里的激活函数还不具有解决线性模型问题的思想，只当做一种对结果的简单处理即可。

10.1.2 训练单层感知机

        If是判断预测是否正确的。If中内容：预测错误了，来更新参数
        Yi是真实值，你真实值为1，预测为1 ，则正确，真实值为-1，预测为-1则正确（注意公式中没加激活函数，所以所得值应该是大于0和小于等于0的值，而并非一定是1和-1，参考最上面的激活函数）。所以可知同号结果大于零，即预测正确；异号结果小于0的话就是错误（对于0，这里如果预测为0，yi又是1预测则错误，yi是-1预测则正确，但代码里只要等于0就需要调整，不确定为什么没区分这点）。
        更新参数使用的就是梯度下降，最下面是使用的损失函数。Max的作用是，预测正确y为正数，-y为负，这max为0。预测错误，y为负，-y为正，则结果为-y值。然后求导得梯度再减去梯度就得到上面w的更新公式了。（b的更新我没有找到如何计算出来的，如果损失函数中是+b的话，那就能算出上面的更新公式了，有人说是放到w里了）

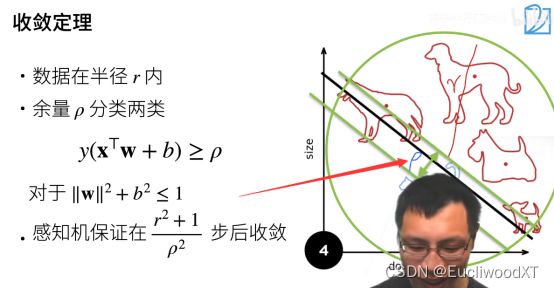
10.1.3 单层感知机的收敛定理

        Y>=0，分类正确（不该是大于0吗）。ρ这里是一个大于零的值，所以可以看成余量...
        r：可理解为数据大小。越大越不容易收敛，因为数据过多。
        ρ：可理解为数据是否分得很开（看图中ρ的位置）。越大约容易收敛，因为不同类别数据分得很开。

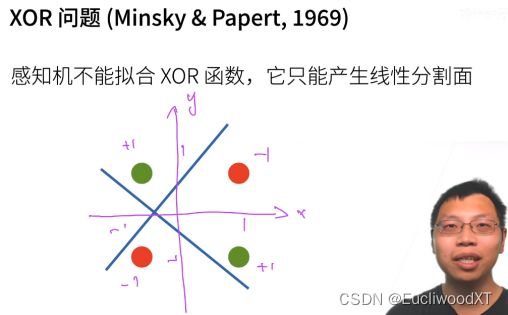
10.1.4 单层感知机存在的问题

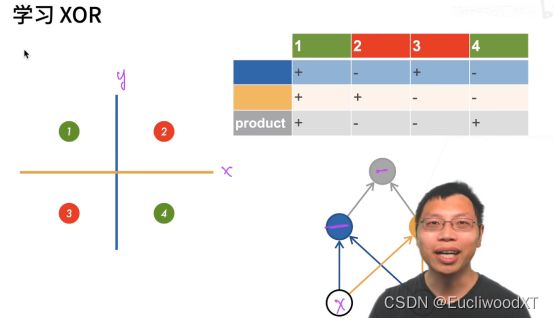
        XOR函数就是这种，如x,y相同是一类，不同是一类，即图中，红点和绿点两类。感知机的线性分割面无法分开。
        关于分割面为什么是条线，考虑二维和三维函数图像大概能理解一些。

10.1.5 总结

10.2 多层感知机（MLP，multi-layer perceptron）

10.2.1 XOR问题解决方法

        先蓝分，后绿分，最后再组合。product是分类结果。
        【理解】：下面就是实现部分了，即参考上图右下角的结构。我感觉吧，人们找到了上图蓝绿划分的方法，然后就暴力带入了感知机，形成了右下角结构雏形，进而演化成下面的加入隐藏层的感知机。

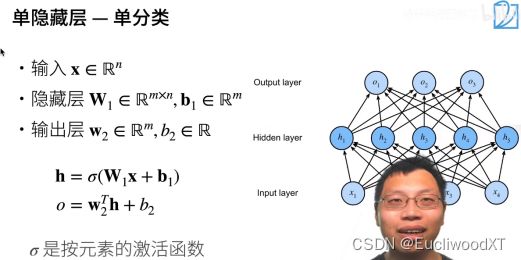
10.2.2 单隐藏层-单分类（实现）

        左右图无必然关系。左图参数输出层只有一个节点。

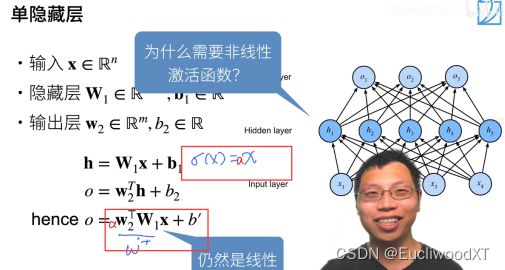
        若还是线性，则其等价于一个单层的感知机。

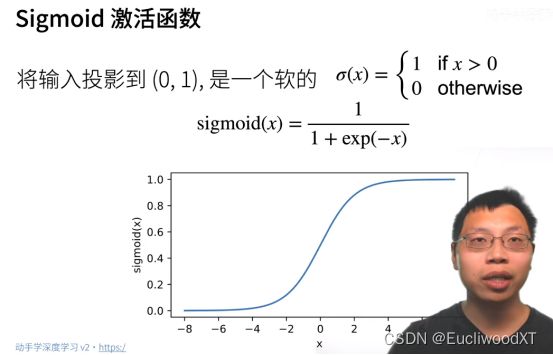
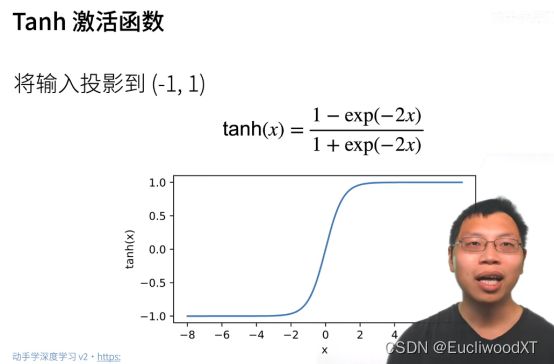
10.2.3 激活函数

        【理解】：加入非线性的激活函数，就是为了让最终函数模型为非线性的，低一维度的自变量空间区域形成自由度更好的划分曲线，以此来更好的划分输入特征。（这里要换个角度看，把权重、偏移看成函数的常数，把特征值看为自变量）

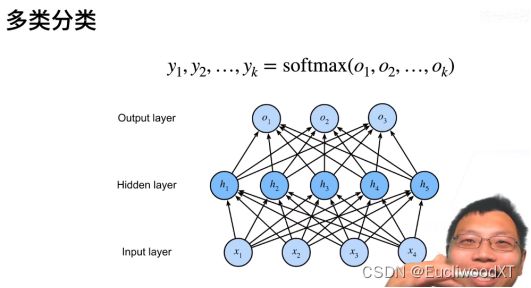
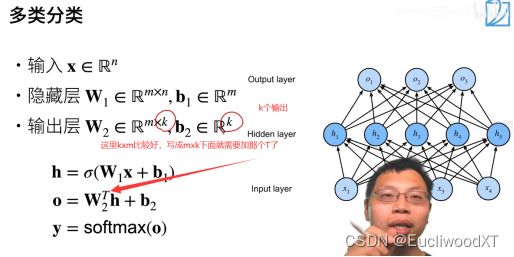
10.2.4 单隐藏层-多分类

        没有中间那一层就是softmax回归，加了就成了多层感知机。

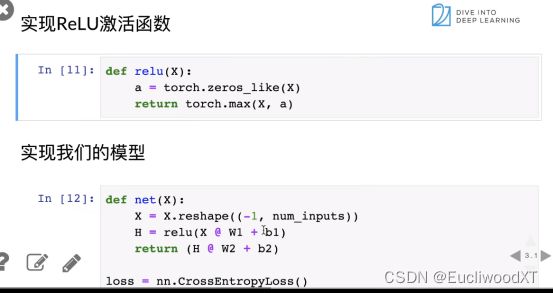
10.2.5 多隐藏层

        最后一层不需要激活函数，激活函数是防止层数塌陷，即加了那么多隐藏层结果还是线性的，就跟单层感知机一样了，这就是塌陷了。所以这里我们加了三层隐藏层，就用了三个激活函数，防止每层的塌陷。
        我感觉最后一层就算加了也没事吧，图中这样可能只是看起来比较规范吧，毕竟单层感知机本身是不加这种激活函数的，最最前面讲的是加了，但我认为那只是单纯的把结果转为1或-1方便观察罢了，并不是这种意义的激活函数。

10.2.6 总结

10.3 代码实现

10.3.1 从零实现

10.3.1.1 批次大小，数据集

        导入包。批次大小指定。导入训练集、测试集。

10.3.1.2 每层单元个数，权重参数

        指定输入、输出、隐藏单元个数。这里是一个三层感知机→输入，隐藏，输出。

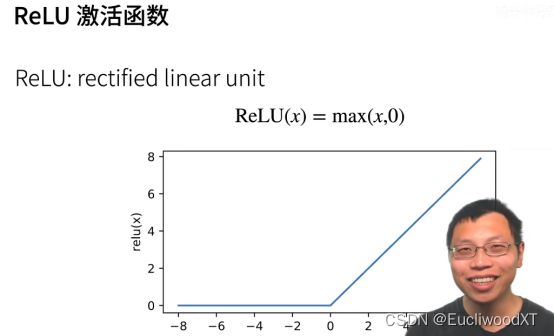
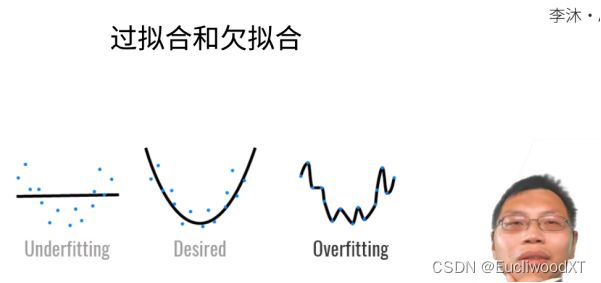
10.3.1.3 ReLU函数，模型定义

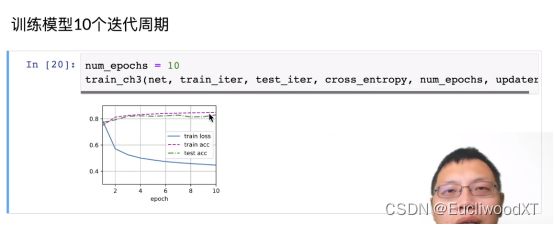
10.3.1.4 训练

10.3.2 简洁实现

11 模型选择+过拟合和欠拟合

11.1 模型选择

11.1.1 训练误差、泛化误差

11.1.2 验证数据集、测试数据集

        【重要】
        训练，相当于日常学习。
        验证数据集，相当于模拟考试，但不公布答案只给分数，然后自己再查漏补缺（调超参数），再进行一次同样试卷的模拟考试，同样不公布答案只给分数，不断查漏补缺让自己最终取得好成绩。
        测试数据集，相当于高考，或者换成模考也行，只不过试卷每次都不一样，绝不会让你做第二次，就是为了提供这种没有准备的未知性。

11.1.3 K-折交叉验证

        如图，分为三块，1/2/3是三次训练（注意是训练），后面则是每块的职责（验证或训练）。然后对所有验证误差取平均值作为最终结果。
        一般来说，K越大越好，但很贵。
        下面（不确定感觉有问题【？】）
        我的理解：我们平常训练把训练与验证数据集全用一次是一次训练。然后这里相当于把一次训练扩为了多次训练（k次）。然后它们虽然训练次数不同，但前后两者都算是一轮训练。一轮→一次训练；一轮→多次训练。
        我的理解：或者是，k次训练，每次都是很多轮训练，即每次都得到最终模型（或者说评测值、误差值），最终有k个模型（误差值），求平均误差作为最终误差来评测模型。一般会设置多组超参数来交叉验证，一组超参（可以理解为一个模型架构，目的是通过K交叉验证选择最好的模型架构）对应一个最终误差，根据结果选取一组好的超参数。然后用这组超参数在整个训练集（数据不够，所以先验证选择模型架构，后使用整个训练集训练）上进行训练。
        目前来看，第二个理解是符合李沐说的。但用途有很多（QA中说的），可以是选择超参数整个数据集训练（一般来说这个才是正宗交叉验证）；或是直接选取k个模型中最好的；或是k个模型全拿来用，输入数据到k个模型中进行预测，输出k个预测值，然后取均值得最终预测。就是第二个理解，李宏毅课上讲了，而且也说了交叉验证也可以用来防止我们val选的不好这种情况（因为对多种val的选择的结果误差值进行了平均评测）。这里讲得不是很清晰，可以去看李宏毅的课P10。
        PS：交叉验证的作用：充分利用训练集；更好的评测模型（两者不是一定绑定执行的）。

11.1.4 总结

11.2 过拟合和欠拟合

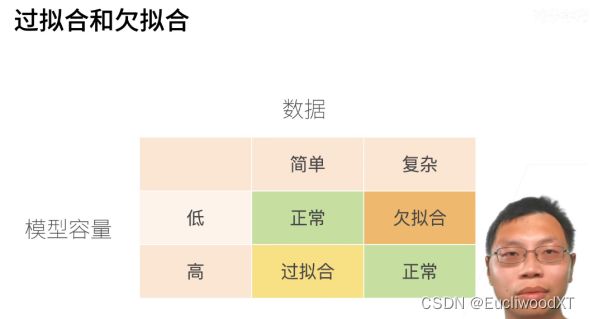
11.2.1 过拟合、欠拟合

        模型容量，也可以理解为能力。

11.2.2 模型容量

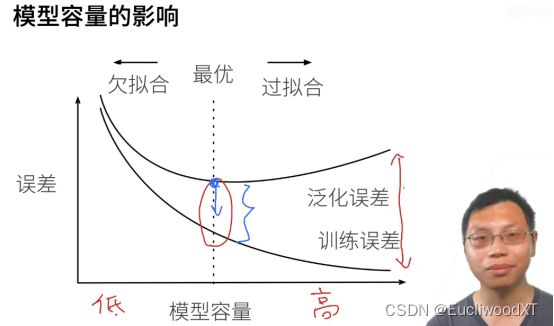
11.2.3 模型容量的影响

        选取训练误差与泛化误差之间比较合适的位置。训练误差理论上可以归0的。
        我们希望中奖的那个高度变小，这也是我们的目的。
        深度学习的一个核心：模型容量要足够大，然后通过各种手段控制容量，实现泛化误差往下降。（弹幕：意思是首先，模型要复杂，过拟合了再想办法解决过拟合问题呗）

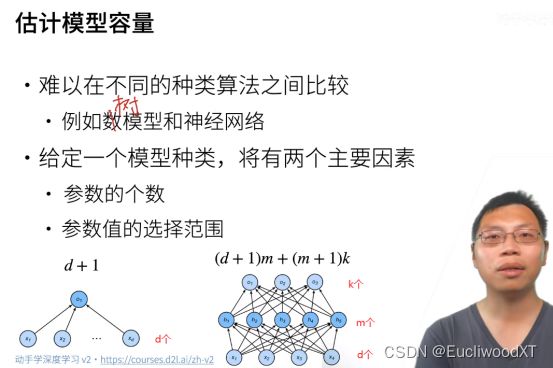
11.2.4 估计模型容量

        d是权重参数；1是偏移参数（bias）。
        按照计算过程来看（好理解）：d+1是生成中间一层一个结点的所需参数，然后中间结点有m个，故是(d+1)m，(m+1)k同理。

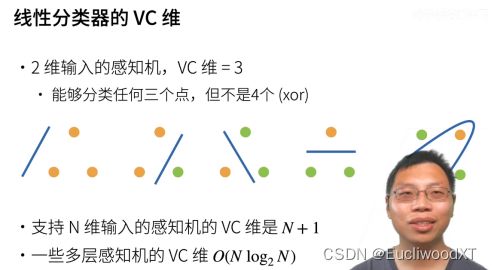
11.2.5 VC维？？？

        【？】
        这里，2维是两个输入一个输出的意思。

11.2.6 VC维的用处

11.2.7 数据复杂度

11.2.8 总结

11.3 代码演示

        略，具体看视频讲解吧，主要是演示过拟合与欠拟合。

12 权重衰退

12.1 权重衰退

12.1.1 均方范数，作为硬性限制

• 最小化损失函数时，加入对w的限制条件。
• 注意w是张量（这里应该是向量，因为这里b是一个标量）。
• w越大，模型越复杂。这里限制w的大小，简化模型。

为什么要权重衰退？

1. 防止过拟合（我的理解，本质上也是噪音造成的）。
2. 弹幕：噪声（样本的）会使得模型复杂化，所以不考虑权重衰退一定会考虑到噪音，模型一定会偏于复杂。（所以这里就需要权重衰退来简单化）
3. 这种噪声复杂化了模型即是过拟合。模型容量大，数据又简单，所以把噪声也完全学习了，就如上图中蓝色波浪线的峰点就是噪声，这样就造成了模型复杂化，即过拟合。

12.1.2 均方范数，作为柔性限制

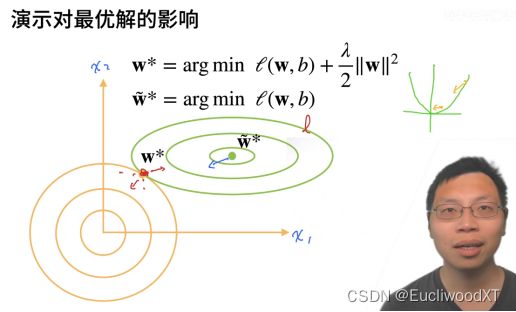
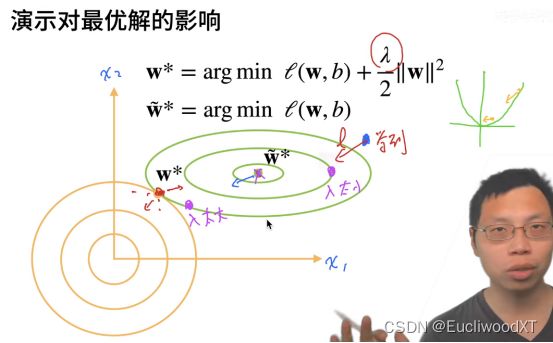
12.1.3 演示对最优解的影响（图解）

        这块复习时，去看视频，笔记记不清楚。
        注意w*并不是原模型真正最优解，原模型真正最优解还是带~的那个，这里只是演示加上正则项（限制）后对我们求得的最优解的影响。
评论：
        李沐老师对于拉格朗日乘子法并没有深入的研究，所以在这个地方没有讲的很清楚。我尝试着补充一下，供大家参考。
        拉格朗日乘子法原本是用于解决约束条件下的多元函数极值问题。举例，求f(x,y)的最小值，但是有约束C(x,y) = 0。乘子法给的一般思路是，构造一个新的函数g(x,y,λ) = f(x,y) +λC(x,y)，当同时满足g'x = g'y = 0时，函数取到最小值。这件结论的几何含义是，当f(x,y)与C(x,y)的等高线相切时，取到最小值。
        具体到机器学习这里，C(x,y) = w^2 -θ。所以视频中的黄色圆圈，代表不同θ下的约束条件。θ越小，则最终的parameter离原点越近。（我的理解：θ越小值c值越大，f模型不变的情况下，c的模型发生改变，值变大时原相切等高线不在相切，c的内部等高线增高与f在此处的高等高线相切，新的最优解诞生，靠近了原点。）

        这里是说明：理论最优解是w~，但因为噪声原因，实际上我们没法学到w~位置，噪声使模型复杂化，我们最终学到右上角的蓝点位置，然后通过权重衰退简化模型往左下角拉，λ太小，λ合适，λ太大，分别对应从右上角第二蓝点到左下角蓝点。

12.1.4 参数更新法则（具体到梯度下降计算）

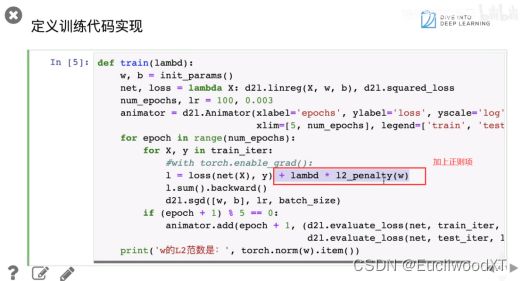
        跟以前的区别：图中下部公式中“红线”标出的内容。
        要结合前面的具体图形来看，在这个公式中，wt前括号中的内容使得每次wt都会有所减小，结合前面的图来看，wt+1的结果会一直往小的方向前行，直到平衡点，在这一点时，wt的减小与后面减去梯度所带来的增加抵消，处于平衡。这即是权重衰退，相比于原来我们的w有所衰退，括号中的内容就是权重衰退的核心。

12.1.5 总结

        λ是控制模型复杂度的超参数。

12.2 代码实现

12.2.1 从零开始

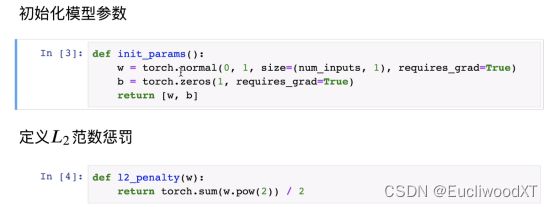
        xi是随机的数。

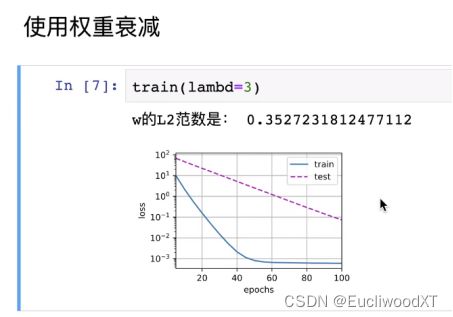
        具体λ值取什么比较好，就要自己测试了。一般1e的-2次方、1e的-3次方等。

12.2.2 简洁实现

        简洁实现中，想加上权重衰退的话，要在优化算法方法中设置新参数，如上图所示。

        因为生成的数据中有随机数据的影响，这里在20 epoch损失就趋于平稳了。

13 丢弃法（drop out）

13.1 丢弃法

13.1.1 动机

        在数据中加入噪音，等价于一个正则。实际上跟权重衰退目的一样，都是防止过拟合。

13.1.2 如何计算

• X’和x期望不变。右边是公式推导，说明了期望没有变化。
• 下面是概率p，某一x置为0，否则执行如图计算。

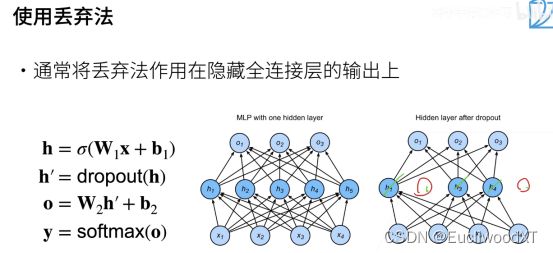
13.1.3 具体使用

        图上虽然是丢弃了，但只是置为0，权重本身还是存在的，参与计算的。

13.1.4 推理中的丢弃法

• 正则项，只在训练中使用。不管是L2正则还是这个正则。
• 正则项只是为了训练参数，获得较好参数后，我们便不再需要正则项了，而是参数与原模型（不含正则项）的结合来进行预测。

13.1.5 总结

        常用于全连接层，在CNN（这里说卷积层比较合适）上用的不多。

13.2 代码实现

13.2.1 从零开始

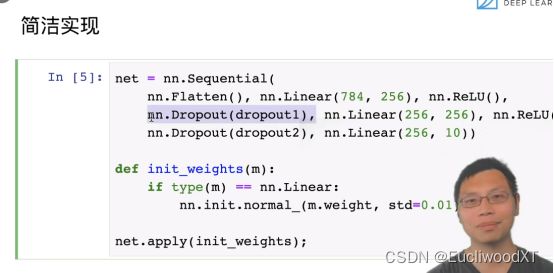
13.2.2 简洁实现

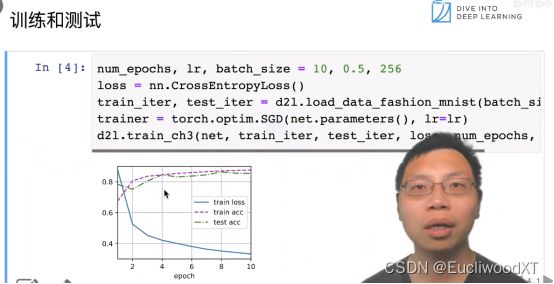
        【小技巧】：设大隐藏层，调大dropout，可能比小隐藏层不用dropout效果好。（例如64神经元的隐藏层，不用dropout，然后改为128神经元的隐藏层用0.5的dropout）

14 结束语

        就到十三课了，后面十四课就记了一半，再往后就没记了。这感觉只能算是视频截图+注释。总之还是去看视频教程吧，搞深度学习还是要好好学一学，不要因为是黑盒就想着不去了解原理，不然调参都不知道怎么调。