Cartographe纯雷达计算位姿的前后端总结
转载 @梦凝小筑本人的研究方向为激光 SLAM,因此对于 Google Cartographer 的经典算法十分感兴趣,但是苦于该算法的论文是英文写作,且该论文有着公式多,解释少的特点。
本人的研究方向为激光 SLAM,因此对于 Google Cartographer 的经典算法十分感兴趣,但是苦于该算法的论文是英文写作,且该论文有着公式多,解释少的特点。因此在看了原论文和网上的各种论文解读,都没有能够完全把这块硬骨头吃下去。
机缘巧合,本人研究生课程高等运筹学大作业需要运用和 Google Cartographer 中的闭环检测 相同的方法,结合 Cartographer 的源代码,才彻底将 Cartographer 论文搞懂。因此在这里写一篇比较完整的总结,方便大家相互学习讨论!
贴出本人参考的一些链接
官方资料 1:https://google-cartographer-ros.readthedocs.io/en/latest/going_further.html
官方资料 2:https://google-cartographer.readthedocs.io/en/latest/
论文链接 1:https://static.googleusercontent.com/media/research.google.com/zh-CN//pubs/archive/45466.pdf
论文链接 2:https://april.eecs.umich.edu/pdfs/olson2009icra.pdf
参考链接:https://zhehangt.github.io/2017/05/01/SLAM/Cartographer/CartographerPaper/
Cartographer 论文解读
一、Introduction
在建图上应用 SLAM 并不是一个新的概念,这里不再作为本文的重点。
本文的贡献在于:提出了一种新的基于激光数据的回环检测方法,这种方法可以减少计算量,可以满足大空间的建图需要,并且对大规模数据进行实时优化。
hector 并没有应用到回环检测,而 google 在此基础上进行改进,并应用上了回环检测,,还是值得学习和借鉴的。
二、Related Work
相关工作不再赘述,直接搬用索哥的总结
相关工作中首先介绍了 scan matching 的几种方法:
1.scan-to-scan matching 是基于激光 SLAM 中最常用来估计相关位姿的。但是非常容易造成累积误差。
2.scan-to-map matching 可以减少累积误差,因为 scan-to-map 每次都通过高斯 - 牛顿法获得局部最优的位姿,前提是要有一个比较好的初始化位姿估计
3.pixel-accurate scan matching 可以进一步减小局部误差,但是计算量比较大。这个方法同样可以用来检测回环。
4. 从 laser scan 中提取特征,从而减少计算量。histogram-based matching 用于回环检测。用机器学习做 laser scan 的特征检测。
之后介绍了处理累积误差的两种方式
1. 基于粒子滤波的优化。粒子滤波在处理大场景地图时,由于粒子数的极具增长造成资源密集。
2. 基于位姿图的优化。与视觉 SLAM 的位姿图优化大同小异,主要是在观测方程上的区别。
三、System Overview
Cartographer 能产生一个精度为 5cm 的 2D 栅格地图。
Cartographer 在前端匹配环节区别与其它建图算法的主要是使用了 Submap 这一概念,每当或得一次 laser scan 的数据后,便与当前最近建立的 Submap 去进行匹配,使这一帧的 laser scan 数据插入到 Submap 上最优的位置。(这里用的是高斯牛顿解最小二乘问题)在不断插入新数据帧的同时该 Submap 也得到了更新。一定量的数据组合成为一个 Submap,当不再有新的 scan 插入到 Submap 时,就认为这个 submap 已经创建完成,接着会去创建下一个 submap,具体过程如下图。(这里没有理解什么情况下新的 scan 不会再匹配到该 Submap 上)
![]()
因此这里 scan matching 的本质是当前 laser scan 与多个邻近的 laser scan 之间进行的。
通过 scan matching 得到的位姿估计在短时间内是可靠的,但是长时间会有累积误差。因此 Cartographer 应用了回环检测对累积误差进行优化。所有创建完成的 submap 以及当前的 laser scan 都会用作回环检测的 scan matching。如果当前的 scan 和所有已创建完成的 submap 在距离上足够近,则进行回环检测。这里为了减少计算量,提高实时回环检测的效率,Cartographer 应用了 branch and bound(分支定界) 优化方法进行优化搜索。如果得到一个足够好的匹配,则会将该匹配的闭环约束加入到所有 Submap 的姿态优化上。
四、LOCAL 2D SLAM
Cartographer 结合了 local 和 global 两种方式进行 2d SLAM。
local 方式就是前端匹配中通过 submap 进行 scan matching。
global 方式就是回环检测,因为是对全局的 submap 进行匹配
scans 中的每个点束的姿态被表示为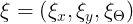,
A、Scans
一个 scans 即激光点云图,包含一个起点和许多的终点。起点称为 origin,终点称为 scan points,用 H 表示点云集,其表达形式如下。
![]()
当获得一个新的 scans,并且要插入到 submap 中时,scans 中点集在 submap 中的位置被表示成 ,其转换公式如下:
![]()
B、Submaps
一个 submap 是通过几个连续的 scans 创建而成的,由 5cm*5cm 大小的概率栅格 构造而成,submap 在创建完成时,栅格概率小于表示该点无障碍,在与之间表示未知,大于表示该点有障碍。每一帧的 scans 都会生成一组称为 hits 的栅格点和一组称为 misses 的栅格点 , 如图所示。
![]()
其中阴影带叉的表示 hits, 阴影不带叉的表示 misses, 每个 hits 中的栅格点被赋予初值, 每个 misses 中的栅格点被称为, 如果该栅格点在先前已经有值,则用下述对该栅格点的值进行更新(此处为,类似)。
![]()
其中 clamp 是区间限定函数。
C、Ceres scan matching
每次获得的最新的 scan 需要插入到 submap 中最优的位置,使我们 scan 中的点束的位姿经过转换后落到 submap 中时,每个点的信度和最高。通过 scan matching 对进行优化,这里的优化问题为解最小二乘问题,其问题描述可表示为:
其中 是线性评价函数,方法为双三次插值法,该函数的输出结果为(0,1)以内的数,在这之外的数可以生成,但不被考虑进去,通过这种平滑函数的优化,能够提供比栅格分辨率更好的精度。该最小二乘问题在 cartogrper 中通过 google 自家的 Ceres 库进行求解。
五、Closing Loops
Cartographer 通过创建大量的 submap 来实现大场景建图,submap 在短时间内的准确度是可靠的,但长时间会存在累积误差,为了消除累积误差,需要通过回环检测来优化所有 submap 的位姿。
A、Optimization problem
回环的优化问题同样为非线性最小二乘问题,其问题描述可表示为:
![]()
其中
Ξm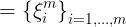 是 submap 的位姿
Ξs 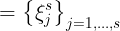是 scan 的位姿
这些位姿是在世界坐标系下的。submap 位姿和 scan 位姿之间存在约束条件
表示 scan 在 submap 坐标系下的位姿,描述 scan 在哪一个 submap 坐标匹配,是相应的协方差矩阵
残差 E 的计算公式如下:
![]()
个人理解:
首先回环优化,我们需要检测到回环,再进行优化。如何检测回环呢,前文也提到过,如果当前的 scan 和所有已创建完成的 submap 中的某个 laser scan 的位姿在距离上足够近,那么通过某种 scan match 策略就会找到该闭环。这里为了减少计算量,提高实时回环检测的效率,Cartographer 应用了 branch and bound(分支定界) 优化方法进行优化搜索,如果得到一个足够好的匹配,到此处,回环检测部分已经结束了,已经检测到了回环得存在。接下来要根据当前 scan 的位姿和匹配到得最接近的 submap 中的某一个位姿来对所有的 submap 中的位姿进行优化,即使残差 E 最小。回环检测与回环优化过程中 scan 和 submap 的关系如图所示:
![]()
即优化 local 中的 submap 与 gloab 中的 submap 之间的位姿的误差,又因为所有的 submap 位姿存在着约束,因此,即是对所有 submap 的位姿进行优化,使 error 最小。
B、Branch-and-bound scan matching
回环检测即是一种匹配过程,即当获得新的 scan 时,在其附近一定范围搜索最优匹配帧,若该最优匹配帧符合要求,则认为是一个回环。首先,该匹配问题可以描述为如下式子:
![]()
其中 W 是搜索空间,是该点对应的栅格点的 M 值,该式子可理解为对于 scan 中的每一个点束插在该 submap 上时的信度和,信度越高则认为越相似,我们需要在 W 空间中寻找出该信度和最大的匹配帧。
因此需要在 W 空间中寻找出 pixel-accurate match 的最优解。
显然有一种方法是暴力匹配法,即在搜索空间范围内中的每一帧与当前帧进行计算 BBS 式子的数值,求出最大值。
对于暴力匹配法来说,该方法的搜索步长为 1。我们假定搜索空间 W
![]()
步长 r =1 , 因此
  
![]()
其中 , 搜索空间是 7m*7m
暴力匹配的 algorithm 如下 ,这样逐个遍历的方法显然是缓慢的
![]()
*branch and bound
为了提高搜索效率,Cartogrpher 采用了 branch and bound(分支定界) 的方法,本人研一课程高等运筹学也运用了该方法求解整数规划问题,在大作业中,我也运用该方法求解了 JSP 问题,主要思路来源也是参考 Cartogrpher 这部分算法的源代码。首先我简单讲解下 branch and bound 对该方法比较熟悉的读者可跳过。
分枝界限法是由三栖学者查理德 · 卡普(Richard M.Karp)在 20 世纪 60 年代发明,成功求解含有 65 个城市的旅行商问题,创当时的记录。“分枝界限法” 把问题的可行解展开如树的分枝,再经由各个分枝中寻找最佳解。
其主要思想:把全部可行的解空间不断分割为越来越小的子集(称为分支),并为每个子集内的解的值计算一个下界或上界(称为定界)。在每次分支后,对凡是界限超出已知可行解值那些子集不再做进一步分支。这样,解的许多子集(即搜索树上的许多结点)就可以不予考虑了,从而缩小了搜索范围。
或许有些读者还是不太理解,下面贴一张图进行讲解。
![]()
这张图就已经比较好的描述了分支定界的思想,还有它为什么能够缩小搜索范围的情况下依然能求到最优解。若先前提到的暴力匹配是枚举法,则分支定界是一种隐式枚举法,。
分支定界进行分支的过程,是不断提高搜索精度的过程,或者可以说增加约束的过程,整个分支树的最底层的所有枚举情况,便是最高搜索精度的枚举集合,便是暴力匹配搜索范围的全部整搜索空间。但是分支定界并没有真正的去求解所有枚举情况的目标函数(BBS)值。
再来看这张图假设我们需要去计算检测匹配的点为如图所示 16 个
则我们第一层搜索精度最低,只列举其中两个,并优先考虑靠左(优先考虑可能性最高的)。
对其继续分层,将其精度提高一倍,又可以列举出两个,并优先考虑靠左。
这样直至最底层,计算出该情况下的目标函数 BBS(值),最左的底层有两个值 A 和 B,我们求出最大值,并将其视为 best_score
然后我们返回上一层还未来得及展开的 C,计算 C 的目标函数 BBS(值) 并让它与 best_score 比较,若 best_score 依旧最大,则不再考虑 C,即不对其进行分层讨论。
若 C 的目标函数 BBS(值) 更大,则对其进行分层,计算 D 和 E 的值,我们假设 D 值大于 E,则将 D 与 best_score 对比
若 D 最大,则将 D 视为 best_score,否则继续返回搜索。
将此算法应用在我们的回环检测中,现已知我们的搜索范围(搜索最高精度,最底层),设置步长来对该问题进行优化搜索。
a, 首先计算顶层线性搜索空间:
假设 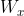= 1000 则 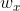= 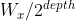
其中 depth 是自己定义的,如果是 8, 顶层步长 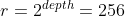
那么顶层的线性搜索空间大小就是 1000/256,大约为 4
角度搜索步长由 cell 大小(1 pixel),和 scan 的最大扫描距离决定,大约为 300
所以顶层 candidate 数量是:4×4×300
论文中用下面两个公式规定了步长的范围
![]()
![]()
b,计算其余层结构
一个 candidate 可构建四个子 Candidate。
角度参数不变
对 x_index_offset,y_index_offset 加入新的偏移量
C 层搜索空间:
![]()
![]()
c,搜索算法
1,构建顶层 C0,计算所有 C0 的 target 得分,从大到小排序
2,C0 C1 , 计算这四新的 C1 的 target 得分,从大到小排序
3,重复步骤 2 ,直到 depth = Max , 得到最底层的四个 Cdepth 并计算 target 得分,得分最高的作为 best_score
4,返回倒数第二层,将 best_score 与剩下三个 Cdepth-1 比较,若 best_score 大于任何一个得分,则无须进入其它分支,继续返回 best_score
5,重复 4 直到遍历整个分支树 返回的结果为最优结果
论文中的伪代码如下:
![]()
下面贴出 Cartogrpher branch and bound 的核心源代码和部分注释
Candidate2D FastCorrelativeScanMatcher2D::BranchAndBound(
const std::vector& discrete_scans,
const SearchParameters& search_parameters,
const std::vector& candidates, const int candidate_depth,
if (candidate_depth == 0) {
// Return the best candidate.
return *candidates.begin();
Candidate2D best_high_resolution_candidate(0, 0, 0, search_parameters);//讨论分层并计算目标函数值
best_high_resolution_candidate.score = min_score;//更新下best score
for (const Candidate2D& candidate : candidates) { //在分支定界中for循环用来分层
if (candidate.score <= min_score) { //若该值不优,则减枝
std::vector higher_resolution_candidates;
const int half_width = 1 << (candidate_depth - 1);
for (int x_offset : {0, half_width}) {
if (candidate.x_index_offset + x_offset >
search_parameters.linear_bounds[candidate.scan_index].max_x) {
for (int y_offset : {0, half_width}) {
if (candidate.y_index_offset + y_offset >
search_parameters.linear_bounds[candidate.scan_index].max_y) {
higher_resolution_candidates.emplace_back(
candidate.scan_index, candidate.x_index_offset + x_offset,
candidate.y_index_offset + y_offset, search_parameters);
ScoreCandidates(precomputation_grid_stack_->Get(candidate_depth - 1),
discrete_scans, search_parameters,
&higher_resolution_candidates);
best_high_resolution_candidate = std::max(
best_high_resolution_candidate,
BranchAndBound(discrete_scans, search_parameters,
higher_resolution_candidates, candidate_depth - 1,
best_high_resolution_candidate.score));
return best_high_resolution_candidate;
后面是一些结果对比,大家自行看论文。
前面写的部分不错, 需要补存几点:
1 Cartography 怎样去除畸的
2 IMU 在前后端是怎样使用
3 如果 ceres scan time 匹配碰见对称环境是怎样解决的
4fast real time scan match 求解约束中线程池怎样做的, 在 SPA 的时候为了保证实时性每帧雷达数据需要 dection loop constraint
5 室外环境的大场景没有办法正常闭环是怎样解决的呢