算法day6
算法day6
- 454.四数相加
- 383.赎金信
- 15.三数之和
- 18.四数之和
454.四数相加
拿到这个题最暴力的想法那肯定就是四个for直接秒了哈哈哈哈。那这样肯定爆时间了。对于这种查找的优化,我这个for带来的主要影响就是遍历查找元素很费时间,所以优化的方式就是用哈希表,实现快速查找。虽然我知道该这么优化,但是我不知道有个操作如何完成,这里有4个数组,我确定了第一个数组我要哪个元素,那我不好确定其他数组我要找哪个元素,如果我这样去做那感觉我还得用三个for。这我就没办法了。直接看题解。
看完题解后我就体会到了用哈希是怎么降时间复杂度的。
直接遍历nums1和nums2求和,然后用哈希表记录求和的值和这种求和方式出现的次数。然后直接去遍历另外两个数组找相反数出现次数,res加这个次数就完事了。
我第一次写的问题:
func fourSumCount(nums1 []int, nums2 []int, nums3 []int, nums4 []int) int {
m1:=make(map[int]bool)
m2:=make(map[int]bool)
for i:=0;i<len(nums1);i++{
for j:=0;j<len(nums2);j++{
m1[nums1[i]+nums2[j]]=true
}
}
for k:=0;k<len(nums3);k++{
for l:=0;l<len(nums4);l++{
m2[nums3[k]+nums4[l]]=true
}
}
res:=0
for key,_ := range m1{
if m2[-key]==true{
res++
}
}
return res
}
我这个代码写的问题就在于,我只判断结果存不存在,但实际上这个结果显然是组合得到的,那就算结果存在那也存在不同的组合。所以这里我就要针对这个问题做一下修改。
修改的办法就是把这个map改了,value改成出现的次数,然后我直接去遍历另外两个数组,然后找相反数映射,把次数都给累加了就完事了。
func fourSumCount(nums1 []int, nums2 []int, nums3 []int, nums4 []int) int {
m1 := make(map[int]int)
for i:=0;i<len(nums1);i++{
for j:=0;j<len(nums2);j++{
m1[nums1[i]+nums2[j]]++
}
}
res:=0
for k:=0;k<len(nums3);k++{
for l:=0;l<len(nums4);l++{
res+= m1[-(nums3[k]+nums4[l])]
}
}
return res
}
这个代码的时间复杂度是O(N^2),这个代码可以看出量级就是两个for
空间最坏达到O(N^2)。空间开销主要就是这个哈希表。
这个哈希表的长度长的可能性就是相加的结果一个重复的都没有,也就是相加后的元素有n平方个。
思考:
之前有用过数组来做哈希表映射的情况,这里到底能不能用数组。
回答:不能,因为数给的范围太大了。太大了就不适合用数组做哈希映射,更适合用map。
小总结:
两个数组两个数组的遍历,这样时间复杂度就降下来了,思考这句话。
这个题目很像前面做过的有效字母的异位词。
用一个容器先遍历一个数组,然后遍历另一个数组的时候看这个容器里有没有想要的元素,这不过这个题编程了两个for循环。
做题的时候,key放什么合适,value放什么合适。思考这个也是做题的突破口。
383.赎金信
拿到这个题我就想到了用哈希表,因为题目里有很多关键的话,给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。还有magazine 中的每个字符只能在 ransomNote 中使用一次。显然有确定某元素是否在另一个字符串中,这个我可以用哈希表来快速的查找。后面这个条件可以确定我的value应该是登记该元素出现的次数。
然后我遍历另外一个字符串的时候我对于进行value–就可以了。还有一旦有map中不存在的元素直接返回false,当遍历的过程中发现有value小于0了就说明元素个数不够,就直接返回false。
func canConstruct(ransomNote string, magazine string) bool {
mapmag:=make(map[rune]int)
for _,value := range magazine{
mapmag[value]++
}
for _,v := range ransomNote{
_,exist := mapmag[v]
if exist == false{
return false
}
mapmag[v]--
if mapmag[v]<0 {
return false
}
}
return true
}
我发现做的这个几个有关哈希的题目,这种思路都非常地类似。
小总结:
这里我要总结的主要是语法上的知识点,虽然学完了go语言基础,但有的语法我并不是了解的很多。关于字符串,很多时候我很想像c++里面那种处理,c++可以直接通过下标访问字符串的字符,但是对于go语言来说是不行的,如果有要访问指定下标的需要,那就必须要转成rune切片,这就变成了c++里面的那种处理方式了,但是在网络编程那一块习惯把字符串转成字节切片,这是因为转成字节切片是ASCII码,这样有方便处理的好处。
然后就是遍历字符串:其实是可以直接遍历字符串的,但是要用到for range,这样也可以实现c++里面那种感觉,但是还是有一定的区别,指定下标就不行,这种就只适合遍历这种应用场景,然后k,v,k是下标,v是rune类型的数据,也就是这个字符。
关于数组模拟哈希表和map,
我虽然知道在少量元素时数组比map好,别的具体细节我就不是很清楚了。这里做一个知识补充:
1.如果键是整数,并且范围比较小,那就可以用数组,因为数组的索引可以直接做键,这样查找、插入、删除操作的时间复杂度可以达到o(1),当键的范围很大的时候,数组就显得浪费空间了,此时应该使用map,map不需要预先知道键的范围。
2.内存使用:实际上map对内存的使用更加高效,因为他只为书记存储的键值对分配内存,数组有些时候你是有未使用的空间的。
3.性能考虑:数据的访问速度通常比map要快,因为map还有个额外的哈希函数计算开销。数组是直接访问内存地址。
4.功能需求:
数组比较适合按索引顺序访问元素
map可以不管这些顺序与否。
如果我对灵活性有更高的需求和较少的内存占用,那么map要好一点。
三数之和
放到一个数组里面我又寄了,问就是三个for,还有像两数之和那种处理,就是两个for外加一个哈希。别的方法我想不到了。然后我就去看题解了。
看完题解后:
1.说是不推荐使用哈希,如果用哈希还真实像我一开始想到的这么处理,但是这样做还有个麻烦的地方就在于去重细节。比如我举个例子,万一题目中出现了这几个结果[-1,0,1],[1,-1,0],[0,1,-1],[0,-1,1]这几个结果里面只要一个,这种切片去重,那就太麻烦了。
本题的比较好理解的解法:双指针
用双指针发就必须要进行排序,这个也和两数之和里面的一个方法思路一样,两数之和也可以排序然后双指针,这也是个很直观的方法。
这是我第一次写的版本:还是有点问题
import "sort"
func threeSum(nums []int) [][]int {
res:=[][]int{}
sort.Slice(nums,func(i,j int)bool{
return nums[i]<nums[j]
})
if len(nums)==0||nums[0]>0{
return [][]int{}
}
for i:=0;i<len(nums);i++{
if i!=0&&nums[i]==nums[i-1]{
continue
}
left,right:=i+1,len(nums)-1
for left<right{
if nums[i]+nums[left]+nums[right]>0{
right--
}else if nums[i]+nums[left]+nums[right]<0{
left++
}else{
if nums[left]!=nums[left+1] && nums[right]!=nums[right-1]{
res = append(res, []int{nums[i],nums[left],nums[right]})
}
}
}
}
if len(res)==0{
return [][]int{}
}else{
return res
}
}
我这个第一次写有好多问题:
1.if i!=0&&nums[i]==nums[i-1]{ continue }
这个地方我第一次写的适合忘记第一个位置不用进行去重判断了,所以这里我不去判断1直接判断后面这个条件,就会发生数组越界,一旦我补上这个条件之后&&有短路的作用,前面这里i!=0就会把后面的条件给短路掉。
2.
for left<right{
if nums[i]+nums[left]+nums[right]>0{
right--
}else if nums[i]+nums[left]+nums[right]<0{
left++
}else{
if nums[left]!=nums[left+1] && nums[right]!=nums[right-1]{
res = append(res, []int{nums[i],nums[left],nums[right]})
}
}
}
这一段的逻辑我没想清楚,正确的逻辑就应该是我已经判断这个结果符合相加等于0了, 但是还要做去重,而且这里我写的逻辑就出现了问题。我后来思考了。
我少考虑了状态:也就是这个数组我本身已经排好序了,那么一开始这个结果我就是要收集下来的,然后才是往中间收缩,在收缩的过程中判重,然后加速收缩。
改正之后的正确版:
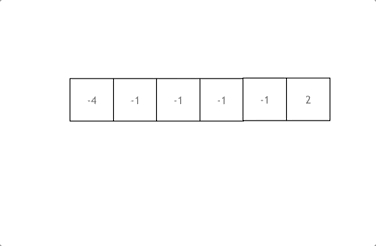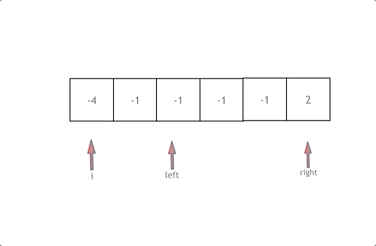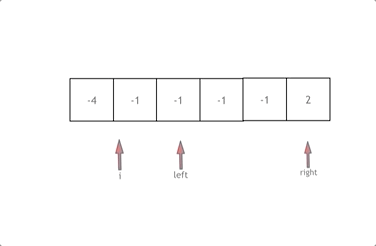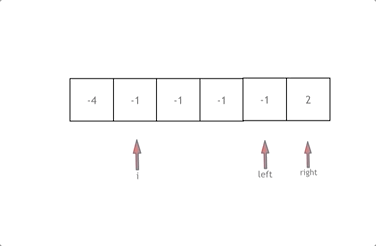
整个代码的逻辑总结,写的时候按上图理解
1.先排序
2.i开始遍历,后面是采用双指针就行left和right的遍历
3.对每一个量的遍历的过程中都要进行去重处理。
import "sort"
func threeSum(nums []int) [][]int {
res:=[][]int{}
sort.Slice(nums,func(i,j int)bool{
return nums[i]<nums[j]
})
if len(nums)==0||nums[0]>0{
return [][]int{}
}
for i:=0;i<len(nums);i++{
if i!=0&&nums[i]==nums[i-1]{
continue
}
left,right:=i+1,len(nums)-1
for left<right{
if nums[i]+nums[left]+nums[right]>0{
right--
}else if nums[i]+nums[left]+nums[right]<0{
left++
}else{
res = append(res, []int{nums[i],nums[left],nums[right]})
for left<right && nums[left]==nums[left+1]{
left++
}
for left<right && nums[right]==nums[right-1]{
right--
}
left++
right--
}
}
}
return res
}
改正后的思考:
res = append(res, []int{nums[i],nums[left],nums[right]})
for left<right && nums[left]==nums[left+1]{
left++
}
for left<right && nums[right]==nums[right-1]{
right--
}
left++
right--
这里的处理就尤为重要,我之前写错就是忘了我是在排好序的状态,接下来我要做的事情就是收集结果,并判重收集结果。由于我的i已经在外层判重了,而且数组还是排好序的状态,所以这里我根本就不用担心nums[i]的结果,所以我判断题目条件得到的第一个结果就可以收集起来,然后接下来就是进行left和right的判重,将left移动到最后一个重复数的时候停止,而且这个数我已经收集了,我还要再left++。
再改进版:
import "sort"
func threeSum(nums []int) [][]int {
res:=[][]int{}
sort.Slice(nums,func(i,j int)bool{
return nums[i]<nums[j]
})
for i:=0;i<len(nums)-2;i++{
if nums[i]>0{
break
}
if i!=0&&nums[i]==nums[i-1]{
continue
}
left,right:=i+1,len(nums)-1
for left<right{
if nums[i]+nums[left]+nums[right]>0{
right--
}else if nums[i]+nums[left]+nums[right]<0{
left++
}else{
res = append(res, []int{nums[i],nums[left],nums[right]})
for left<right && nums[left]==nums[left+1]{
left++
}
for left<right && nums[right]==nums[right-1]{
right--
}
left++
right--
}
}
}
return res
}
我这里加了一个剪枝操作和循环遍历那里len(nums)-2,这是数据决定的,i走不到底的。
if nums[i]>0{
break
}
这样做了之后,后面的nums[i]大于0的部分我就没必要去走了。
注意我之前想剪枝的时候想错了
我写了个if nums[i]>0{return [][]int{}},这纯粹是想错了,我这里的剪枝目的是剪掉后面没必要走的地方。
思考:
1.为什么要排序,排序会带来哪些方便?
2.如何进行去重,双指针做也是要考虑去重的。
3.时间复杂度是多少?
1.排序之后会给双指针的用法带来方便,还可以优化去重的逻辑,这样重复的元素会排在一起,更方便进行去重。能用双指针也给这个题降低了一定的时间复杂度。
2.nums[i],nums[left],nums[right]都要考虑去重,这里由于已经有序了,那么可以看相邻元素是否相同就可以轻松的去重,i就往后移动,left和right判断重复时往内收缩即可。
去重的时候还有很多细节:
nums[i]==nums[i-1]
left
举个例子:
{-1, -1 ,2},这个显然就是一个正确的结果集,如果你这样就会把这个结果continue了。
为什么会出现这样的情况:
我个人的理解是,在我排好序的情况,i即i之前的都是我nums[i]扫过的结果集,而后面的是属于left和right的结果集了,所以这里如果去判后面,换句话说这个结果集本就是不属于i的,i误以为是自己的就进行了去重。
我自己理解为各自的结果集,i,left,right。
下面left和right的去重是一个道理的,left往后判断是因为left后面可以是它的结果集范围,right是前面才是结果集范围。
3.时间复杂度是o(n^2),因为i一个外置for循环,里面套了一个双指针的for循环。
四数之和
这个题的总体思路就是三数之和外面又套了一层,但是有些细节要注意,四数之和不能像三数之和那样剪枝,因为四数之和相加不是等于0而是target。
举个例子:-4,-1,0,2,3,4,target=-5,你像三数之和直接判断nums[i]>-5那就会漏了,所以三数之和的剪枝对于四数之和并不适用,因为两个负数相加是可以变得更小的。这个题要想剪枝就必须改条件,那就是前面我说两个负数相加是可以变得更小这个条件没了,你就可以剪枝,所以带个附加条件,nums[k]>target&&nums[k]>0&&target>0,符合这个条件就可以剪枝。
import "sort"
func fourSum(nums []int, target int) [][]int {
res := [][]int{}
sort.Slice(nums,func (i,j int)bool{
return nums[i]<nums[j]
})
if len(nums) < 4 {
return res
}
for k := 0; k < len(nums)-3; k++ {
if k != 0 && nums[k] == nums[k-1] {
continue
}
for i := k + 1; i < len(nums)-2; i++ {
if i != k+1 && nums[i] == nums[i-1] {
continue
}
left, right := i + 1, len(nums)-1
for left < right {
sum := nums[k] + nums[i] + nums[left] + nums[right]
if sum < target {
left++
} else if sum > target {
right--
} else {
res = append(res, []int{nums[k], nums[i], nums[left], nums[right]})
for left < right && nums[left] == nums[left+1] {
left++
}
for left < right && nums[right] == nums[right-1] {
right--
}
left++
right--
}
}
}
}
return res
}
代码整体逻辑还是很清楚的就是外面一个循环套了个三数之和。
剪枝的版本实在是不好写,我写了好几次剪枝都没写对,先干脆这样吧。
代码的时间复杂度是O(n^3).
分析:排序nlogn
下面这个for循环构成:k一个for,i也是一个for,内部双指针一个for,所以o(N^3)
所以O(N^3)。
总结:
哈希只适合在快速查找元素的时候用,虽然快速查找元素是一个很好的优化,但不是在任何场景下这样优化会是好事,反而会让你的代码很难写出来。所以哈希可以当作一个思路,但不是唯一的思路。