树状数组

　　原文：http://www.cnblogs.com/ws5167/p/3903970.html

 

　　树状数组主要用于快速的更改某个点的值和查询某个区间的和,是一种比较小巧的数据结构.先看下图:

　　　　　　

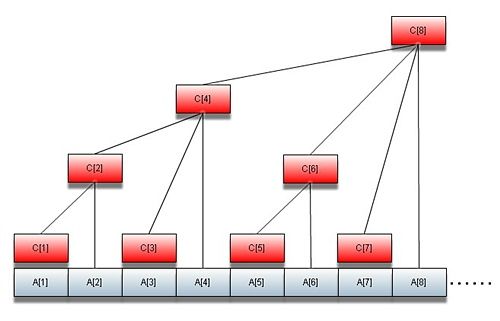
　　假设数组A[]是我们要操作的对象,则数组C[]则是数组A[]相对应的树状数组.观察上图,我们得到数组C[]前八个值:

　　C[1]=A[1]

　　C[2]=A[1]+A[2]

　　C[3]=A[3]

　　C[4]=A[1]+A[2]+A[3]+A[4]

　　C[5]=A[5]

　　C[6]=A[5]+A[6]

　　C[7]=A[1]

　　C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]

.......

　　可以总结一个规律:当 i 为奇数时: C[i]=A[i];当 i 为偶数时: C[i]=A[i-2^k+1]+..A[i](k表示 i 最多有2的k次幂).

　　例如: 6的因子中有2的一次幂,等于2,所以C[6]=A[5]+A[6](由六向前数两个数的和),4的因子中有2的两次幂,等于4,所以C[4]=A[1]+A[2]+A[3]+A[4](由四向前数四个数的和).

　　对于任一个数组对应的树状数组有公式: C[n]=A[n-2^k+1]+....+A[n]（其中k为n的二进制表示中从右往左数的0的个数)

　　对于求2^k有如下代码:

int lowbit(int x)

{

    return x & (-x);

}

　　

　　

　　求区间和操作

　　假设我们要求区间[1,7]的和,用sum(7)表示,观察上图可知: sum(7)=C[7]+C[6]+C[4].
具体代码如下:

// 求区间[1,i]的和

int sum(int i)

{

    int s=0;

    while(i>0)

    {

        s += c[i];

        i -= lowbit(i);

    }

    return s;

}

 

　　更新某个点的值

　　当数组需要变更的时候,树状数组就发挥了它的优势,假设我们要给某个节点 i 的值加上 x.

算法包含两步:

　　① 当 i<=n 时,执行下一步;否则的话,算法结束;

　　② c[i] += x; i+=lowbit(i).

例如,在上面的示意图中,假设更改的元素是a[2],那么它影响到得c数组中的元素有c[2],c[4],c[8],我们只需一层一层往上修改就可以了,这个过程的最坏的复杂度也不过O(logN);

具体代码如下:

 

// 把节点 i 的值加上 x.

void Update(int i, int x)

{

    while(i<=n)

    {

        c[i] += x;

        i += lowbit(i);

    }

}

 

　　 二维树状数组和一维有形似之处,都是从下往上更新，从上往下求和。

int lowbit(int x)

{

    return x&(-x);

}



void update(int x, int y, int val) //将 a[x][y] 的值增加val

{

    for(int i=x; i<N; i+=lowbit(i))

    {

        for(int j=y; j<N; j+=lowbit(j))

        {

            sum[i][j] += val;

        }

    }

}





int getSum(int x, int y) //求以1,1为左上角端点,学校，x,y为右下角端点的矩阵和.

{

    int s = 0;

    for(int i=x; i>0; i-=lowbit(i))

    {

        for(int j=y; j>0; j-=lowbit(j))

        {

            s += sum[i][j];

        }

    }

    return s;

}

View Code

 

　　

------------------------------------------------------------------------------------------------

　　树状数组的应用

　　应用一

　　假如给你一个数组a[ ] = {2,5,3,4,1},求b[i]，b[i] 表示在a[1],a[2]...a[i-1]中(即位置i的左边)小于等于a[i]的数的个数。对此例b[] = {0,1,1,2,0}。 那么该如何去求得b[i]呢？

解法：假如要得到b[4]的值,对于a[4] = 4. 我们 只要得到在a[1],a[2],a[3] 中出现小于等于4的个数，即1,2,3,4的个数,此例即为2. a[1] = 2 < a[4], a[3] = 3 < a[4]. 所以b[4] = 2;其他的以此类推. 求b[i]的值，需要得到在a[1],a[2]....a[i-1]中出现小于等于a[i]的个数，即1,2...a[i]的个数. 相当于求前a[i]项的和，可用到树状数组. 

具体操作:

for(int i=1; i<=n; i++)

{ 

b[i] = getSum(a[i]); //求前a[i]项的和

update(a[i],1);      //第a[i]个元素+1

}

 

　　应用二

　　假如给你一个数组a[ ] = {2,5,3,4,1},求b[i]，b[i] 表示在a[1],a[2]...a[i-1]中(即位置i的左边)大于等于a[i]的数的个数。对此例b[] = {0,0,1,1,4}。 那么该如何去求得b[i]呢？

解法1: 只需要先将数组a倒过来编号，即将a转换为，a[] ={4,1,3,2,5}.此时具体的操作如应用一

解法2:改变更新路径和求和路径

void update(int x, int val)

{

    for(int i=x; i>0; i-=lowbit(i))

    {

        sum[i] += val;

    }

}



int getSum(int x)

{

    int s = 0;

    for(int i=x; i<MAXN; i+=lowbit(i))

    {

        s += sum[i];

    }

    return s;

}

View Code

　　应用三  逆序数

　　假如给你一个数组a[ ] = {2,5,3,4,1},求b[i]，b[i] 表示在a[i],a[i+1]...a[n]中(即位置i的右边)小于等于a[i]的数的个数。对此例b[] = {1,3,1,1,0}。 那么该如何去求得b[i]呢？

　　操作：应用一位置i的左边，应用三是位置i的右边。 然后只需要在应用一的基础上从后往前操作即可.

for(int i=n; i>=1; i--)

{ 

b[i] = getSum(a[i]); //求前a[i]项的和

update(a[i],1);      //第a[i]个元素+1

}

　　应用四

　　假如给你一个数组a[ ] = {2,5,3,4,1},求b[i]，b[i] 表示在a[i],a[i+1]...a[n]中(即位置i的右边)大于等于a[i]的数的个数。对此例b[] = {3,0,1,0,0}。 那么该如何去求得b[i]呢？

　　操作：只需将数组a倒过来编号,即将a转化为 a[]={4,1,3,2,5} 然后利用应用三