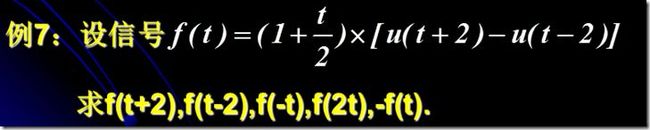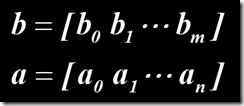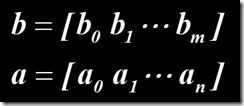MATLAB信号与系统分析（一）——连续时间信号与系统的时域分析

一、连续时间信号的表示：

1、向量表示法：

     在MATLAB中，是用连续信号在等时间间隔点的样值来近似表示连续信号，当取样时间间隔足够小时，这些离散的样值就能较好地近似出连续信号。

     对于连续时间信号f(t)，一般是用两个行向量f和t来表示。t=t1:p:t2 ，t1 表示的是信号的起始时间，t2为终止时间，p为时间的间隔。而f为连续时间f(t)在向量t所定义的时间范围内对应的样值。

2、符号运算表示法：

     使用sym定义变量，然后进行表示。

Eg：分别采用上述两种方法画出抽样信号：

clear all;
t=-10:1.5:10;%取点数比较少，图形会比较失真
f=sin(t)./t;
subplot(2,2,1),plot(t,f)

t=-10:0.1:10;%取点数比较多，图形会比较接近
f=sin(t)./t;
subplot(2,2,2),plot(t,f)

f=sym('sin(t)/t');%采用符号方法
subplot(2,2,3),ezplot(f,[-10 10])
t=-3*pi:pi/100:3*pi;

ft=sinc(t/pi);%直接用malab中的函数
subplot(2,2,4),plot(t,ft)

 

二、一些常用信号的表示：

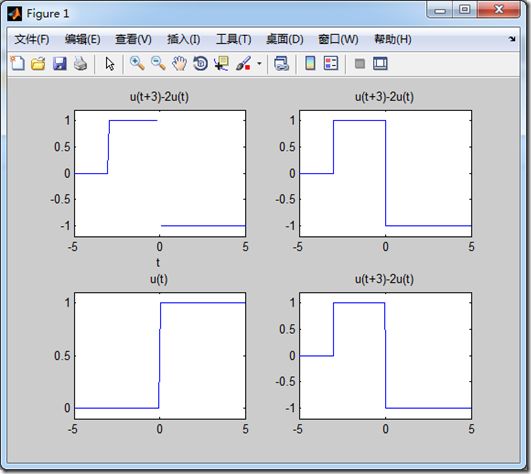
1、单位阶跃信号：

（1）利用符号函数maple中的内核函数Heaviside

（2）利用自编函数Heaviside(t)

function f=Heaviside(t)
f=(t>0);

（3）利用符号函数来生成单位阶跃函数

t=-10:0.1:10;
f=sign(t)/2+0.5;
plot(t,f);
axis([-5,5,-1.2,1.2]);

clear all
%利用maple中的heaviside函数来实现u(t+3)-2u(t)
subplot(2,2,1);
syms t
f=heaviside(t+3)-2*heaviside(t);
ezplot(f,[-3*pi,3*pi])
axis([-5,5,-1.2,1.2]);
title('u(t+3)-2u(t)');

%利用自己编写的heaviside函数来实现u(t+3)-2u(t)
subplot(2,2,2);
t=-5:0.01:5;
f=Heaviside(t+3)-2*Heaviside(t);
plot(t,f);
axis([-5,5,-1.2,1.2]);
title('u(t+3)-2u(t)')

%利用符号函数来实现单位阶跃信号
subplot(2,2,3);
t=-5:0.05:5;
f=sign(t);
ff=1/2+1/2*f;
plot(t,ff);
axis([-5 5 -0.1 1.1]);
title('u(t)')

%利用符号函数来实现u(t+3)-2u(t)
subplot(2,2,4);
t=-5:0.01:5;
f=(1/2+1/2*sign(t+3))-2*(1/2+1/2*sign(t));
plot(t,f),axis([-5,5,-1.2,1.2]),title('u(t+3)-2u(t)')

      PS：由于自己生成的阶跃函数定义u(0)=0，而自带的定义为u(0)=1，所以会出现这种图形没有连接起来的问题。

 

2、MATLAB信号处理工具箱提供的连续信号：

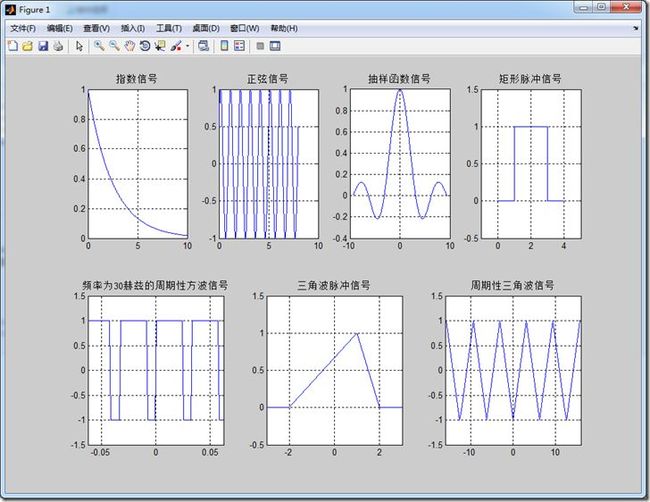
（1）使用MATLAB自带函数生成：

%指数信号的表示y=A*exp(a*t)
subplot(2,4,1);
A=1;
a=-0.4;
t=0:0.01:10;
ft=A*exp(a*t);
plot(t,ft);
title('指数信号')  %要放在plot后面
grid on

%正弦信号y=A*sin(w0*t+phi)
subplot(2,4,2);
A=1;
w0=2*pi;
phi=pi/6;
t=0:0.001:8;
ft=A*sin(w0*t+phi);
plot(t,ft);
title('正弦信号');
grid on;

%抽样函数sinc(t)=sin(pi*t)/pi*t
subplot(2,4,3);
t=-3*pi:pi/100:3*pi;
ft=sinc(t/pi);
plot(t,ft);
title('抽样函数信号');
grid on;

%矩形脉冲信号y=rectpuls(t,width)产生一个幅值为1，宽度为width，相对于t=0点左右对称的矩形波信号
subplot(2,4,4);
t=0:0.001:4;
T=1;
ft=rectpuls(t-2*T,2*T);
plot(t,ft);
axis([-1 5 -0.5 1.5]);  %要放在plot后面
title('矩形脉冲信号');
grid on;

%周期性矩形信号即方波信号y=square(t,DUTY)产生一个周期为2*pi，幅值为1（－1）的周期性方波信号，duty表示占空比
subplot(2,3,4);
t=-0.0625:0.001:0.0625;
ft=square(2*pi*30*t,75);
plot(t,ft);
axis([-0.0625 0.0625 -1.5 1.5]);   
title('频率为30赫兹的周期性方波信号');
grid on;

%三角波脉冲信号y=tripuls(t,width,skew)用以产生一个最大幅度为1，宽度为width，斜度为skew的三角波信号。
%该函数的横坐标范围由向量t决定，是以t=0为中心向左右各展开width/2的范围。
%斜度skew是介于-1和1之间的值，它表示最大幅度1出现所对应的横坐标位置。
%一般地，最大幅度1出现在t=(width/2)×skew的横坐标位置
subplot(2,3,5);
t=-3:0.001:3;
ft=tripuls(t,4,0.5);
plot(t,ft);
axis([-3 3 -0.5 1.5]);   
title('三角波脉冲信号');
grid on;

%周期性三角波信号y=sawtooth(t,width)用以产生一个周期为2*pi，最大幅度为1，最小幅度为-1的周期性三角波信号（又称锯齿波信号）。
%width表示最大幅度出现的位置
subplot(2,3,6);
t=-5*pi:pi/10:5*pi;
ft=sawtooth(t,0.5);
plot(t,ft);
axis([-16 16 -1.5 1.5]);   
title('周期性三角波信号');
grid on;

（2）信号工具函数

%一般周期性脉冲信号y=pulstran(t,d,'func',p1,p2,...)
%t制定pulstran的横坐标范围，向量d用于指定周期性的偏移量（即各个周期的中心点）
%整个pulstran函数的返回值实际上就相当于y=func(t-d(1))+func(t-d(2))+......
%p1，p2...是需要传送给func函数的额外输入参数值（除去时间变量t外），例如rectpuls需要width这个额外参数等

%一般周期性脉冲信号y=pulstran(t,d,'func',p1,p2,...)
%t制定pulstran的横坐标范围，向量d用于指定周期性的偏移量（即各个周期的中心点）
%整个pulstran函数的返回值实际上就相当于y=func(t-d(1))+func(t-d(2))+......
%p1，p2...是需要传送给func函数的额外输入参数值（除去时间变量t外），例如rectpuls需要width这个额外参数等
clear all;
subplot(1,2,1);
t=-0.5:0.001:1.5;
d=0:0.5:1;
y=pulstran(t,d,'rectpuls',0.1);%周期性矩形信号
plot(t,y);
axis([-0.1 1.1 -0.1 1.1]);
title('周期性矩形信号')   
grid on

%周期三角波信号
subplot(1,2,2);
t=-0.2:0.001:1.2;
d=0:1/2:1;
y=pulstran(t,d,'tripuls',0.1,-1);
plot(t,y);
axis([-0.1 1.1 -0.1 1.1]);
title('周期性三角波信号');
grid on;

 

3、复指数信号

例子：

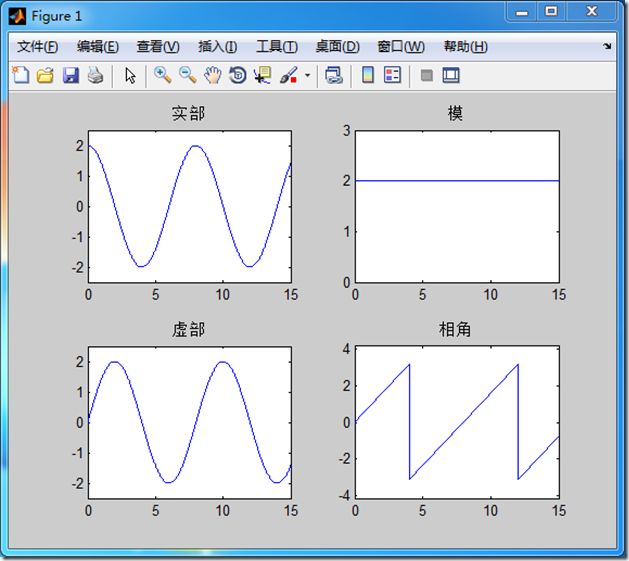
%实现方法一：

%fuction fexp(d,w,t1,t2,a)
%绘制复指数信号时域波形程序
%d：复指数信号复频率实部
%w：复指数信号复频率虚部
%t1：绘制波形的起始时间
%t2：绘制波形的终止时间
%a：复指数信号的幅度
clear all
figure(1);
fexp(0,pi/4,0,15,2);

%实现方法二：
t=0:0.01:15;
a=0;b=pi/4;
z=2*exp((a+i*b)*t);
figure(2)
subplot(2,2,1),plot(t,real(z)),title('实部')
subplot(2,2,3),plot(t,imag(z)),title('虚部') 
subplot(2,2,2),plot(t,abs(z)),title('模')
subplot(2,2,4),plot(t,angle(z)),title('相角')

 

三、连续信号的时域运算、时域变换

1、利用符号运算实现连续信号的时域变换

（1）相加：

s=symadd(f1,f2)%s=f1+f2
ezplot(s)

（2）相乘：

s=symmul(f1,f2)%s=f1*f2
ezplot(s)

（3）移位：

y=subs(f,t,t-t0)%f(t-t0)
y=subs(f,t,t+t0)%f(t+t0)
ezplot(y)

（4）反折：

y=subs(f,t,-t)
ezplot(y)

（5）尺度变换：

y=subs(f,t,a*t)
ezplot(y)

（6）倒相

y=-f
ezplot(y)

clear all
syms t
%f=sym('(t/2+1)*(heaviside(t+2)-heaviside(t-2))')

f=(t/2+1)*(heaviside(t+2)-heaviside(t-2));
subplot(2,3,1),ezplot(f,[-3,3]),title('f(t)')

y1=subs(f,t,t+2)
subplot(2,3,2),ezplot(y1,[-5,1]),title('f(t+2)')

y2=subs(f,t,t-2)
subplot(2,3,3),ezplot(y2,[-1,5]),title('f(t-2)')

y3=subs(f,t,-t)
subplot(2,3,4),ezplot(y3,[-3,3]),title('f(-t)')

y4=subs(f,t,2*t)
subplot(2,3,5),ezplot(y4,[-2,2]),title('f(2*t)')

y5=-f
subplot(2,3,6),ezplot(y5,[-3,3]),title('-f(t)')

 

四、连续系统的冲激响应、阶跃响应

1、冲激响应：

limpulse(b,a)

impulse(b,a,t)

impulse(b,a,t1:p:t2)

y=impulse(b,a,t1:p:t2)

 

2、阶跃响应

step(b,a)
step(b,a,t)
step(b,a,t1:p:t2)
y=step(b,a,t1:p:t2)

      其中：

clear all;
a=[1 5 6];
b=[3 0 2];

%冲击响应
figure(1)
subplot(2,2,1),impulse(b,a)
subplot(2,2,2),impulse(b,a,5) %绘制0～5范围内冲激响应的时域波形
subplot(2,2,3),impulse(b,a,1:0.1:2) %绘制1～2范围内，步长为0.1的冲激响应的时域波形
y1=impulse(b,a,1:0.1:3);%给出数值解
subplot(2,2,4),plot(1:0.1:3,y1)

%阶跃响应
figure(2)
subplot(2,2,1),step(b,a)
subplot(2,2,2),step(b,a,5)
subplot(2,2,3),step(b,a,1:0.1:2)
y2=step(b,a,1:0.1:3);
subplot(2,2,4),plot(1:0.1:3,y2)

 

五、求LTI连续系统的响应

1、零输入响应：

nitial(A,B,C,D,y(0-),t)

2、零状态响应：

Lsim(sys,X,t)
Lsim(b,a,X,t)
Lsim(A,B,C,D,X,t）

3、全响应：

lsim(A,B,C,D,X,t,y(0-))

其中：

微分方程系统函数对象的生成函数：sys=tf(b,a)

微分方程的状态方程系数生成函数： [A,B,C,D]=tf2ss(b,a)

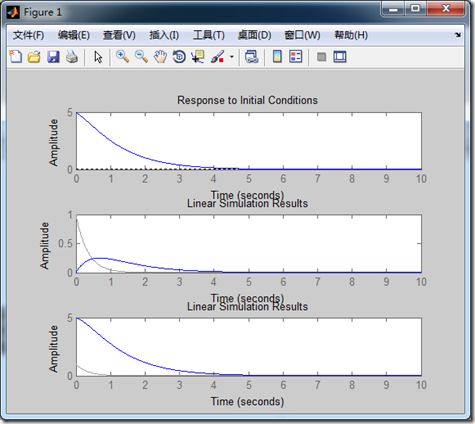
4、例子：

clear all;
a=[1 3 2];
b=[1 3];
t=0:0.01:10;
x=exp(-3*t);
rc=[2,1];
sys=tf(b,a)
[A,B,C,D]=tf2ss(b,a)
figure(1)
subplot(3,1,1),initial(A,B,C,D,rc,t) %零输入响应
subplot(3,1,2),lsim(b,a,x,t)         %零状态响应
subplot(3,1,3),lsim(A,B,C,D,x,t,rc)  %全响应,只能用状态系数来表示系统

 

结果：

sys =
 
      s + 3
  -------------
  s^2 + 3 s + 2
 
Continuous-time transfer function.


A =

    -3    -2
     1     0


B =

     1
     0


C =

     1     3


D =

     0

 

六、两个信号的卷积：

1、自编卷积函数：

function  [f,t]=gggfconv(f1,f2,t1,t2)    
    d=input(‘请输入采样时间间隔: ');
    f=conv(f1,f2);     %计算序列f1和f2的卷积和
    f=f*d; 
    ts=t1(1)+t2(1)   %计算序列f非零值的起始位置
    l=length(t1)+length(t2)-2; %计算序列f非零值的宽带
    t=ts:d:(ts+l*d)      %计算序列f非零值的时间向量
    subplot(2,2,1);plot(t1,f1) 
    subplot(2,2,2);plot(t2,f2)
    subplot(2,2,3);plot(t,f);

2、例子：

clear all;
%计算连续时间信号卷积积分并绘波形
t1=-1:0.01:3;
f1=Heaviside(t1)-Heaviside(t1-2);               %定义信号 
t2=t1;
f2=0.5*t2.*(Heaviside(t2)-Heaviside(t2-2));     %定义信号 
[t,f]=gggfconv(f1,f2,t1,t2);                    %计算卷积积分并绘出时域波形