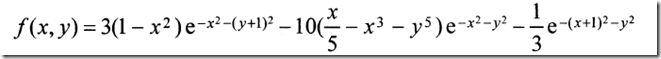MATLAB学习笔记（五）——MATLAB绘图

（一）二维数据曲线图

一、绘制单根二维曲线

1、基本调用格式

plot(x,y)

（1）x,y为长度相同的向量，分别用于储存x坐标和y坐标数据

（2）用于绘制以x,y为横，纵坐标的二维曲线。

（3）举例

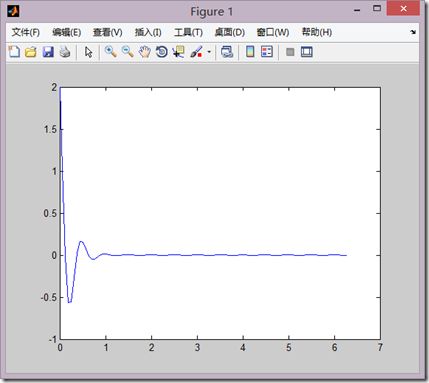
>> x=linspace(0,2*pi,100);
>> y=2*exp(-5*x).*cos(4*pi*x);
>> plot(x,y)

效果如下：

       从这里我们可以明白plot绘图，其实是取点，然后用光滑的曲线进行连接的。可以说是最差的插值方法吧。

2、plot函数最简单的调用格式

plot(x)

（1）x是实向量时，以该向量元素的下标为横坐标，元素为纵坐标画出一条连续曲线，这实际上是绘制折线图。

（2）x是复向量时，以向量元素的实部和虚部为横、纵坐标绘制一条曲线。

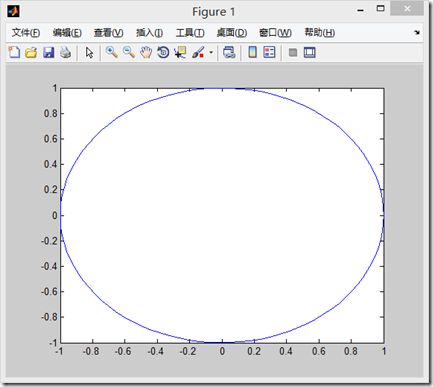
（3）举个例子

>> t=linspace(0,2*pi,100);
>> x=exp(i*t);
>> plot(x)

二、绘制多根二维曲线

1、plot函数的输入参数是矩阵形式

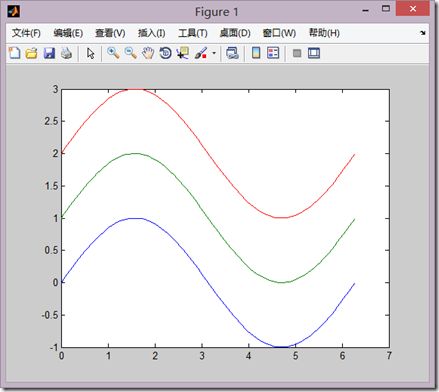
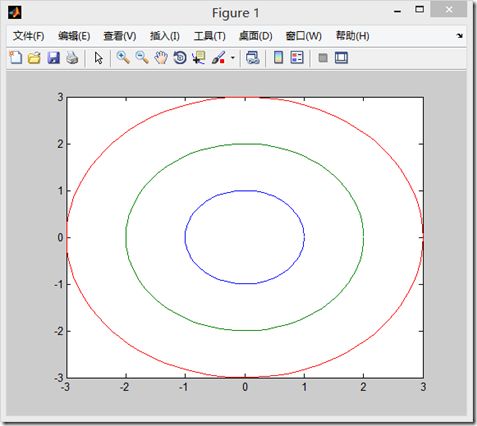
（1）当x是向量，y是有一维与x同维的矩阵时，绘制出多根不同颜色的线。

>> x=linspace(0,2*pi,100);
>> y=[sin(x);
     1+sin(x)
     2+sin(x)];
>> plot(x,y)

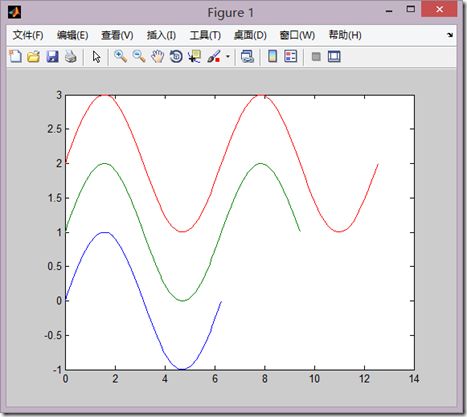
（2）当x,y是同维矩阵时，则以x,y对应列元素为横、纵坐标分别绘制曲线，曲线条数等于列数。

>> x1=linspace(0,2*pi,100);
>> x2=linspace(0,3*pi,100);
>> x3=linspace(0,4*pi,100);
>> x=[x1,x2,x3]';

>> y=[sin(x1);1+sin(x2);2+sin(x3)]‘;
>> plot(x,y)

（3）对只包含一个输入参数的plot函数

a、当输入参数是实矩阵时，则按列绘制每列元素值相对其下标的曲线。

b、当输入参数是复矩阵时，则以实部、虚部为横、纵坐标绘制多条曲线。

t=linspace(0,2*pi,100);
x=exp(i*t);
y=[x;2*x;3*x]';
plot(y)

2、含多个输入参数的plot函数

（1）调用格式为

plot(x1,y1,x2,y2,……,xn,yn)

      可以在同一坐标内画出3条曲线

（2）当输入参数有矩阵形式时，配对的x，y按对应的横纵坐标分别绘制曲线，条数还是等于列数。

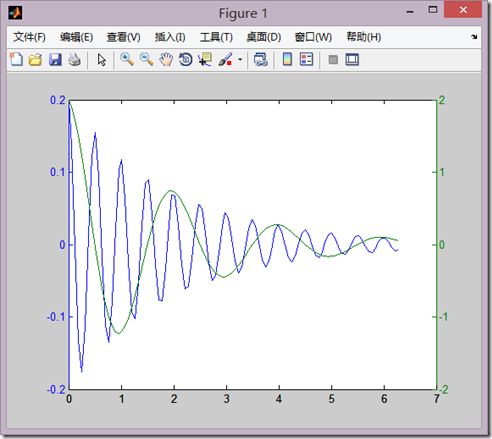
3、具有两个纵坐标标度的图形

（1）调用格式

plotyy(x1,y1,x2,y2)

      其中x1，y1对应一条曲线，而x2和y2对应另外一条曲线，然后左边是第一条曲线的纵坐标，右边是第二条曲线的纵坐标。

（2）实例

>> y1=0.2*exp(-0.5*t).*cos(4*pi*t);
>> y2=2*exp(-0.5*t).*cos(pi*t);
>> plotyy(t,y1,t,y2);

4、图形保持

     一般情况下，每执行一次命令就刷新当前窗口，图形窗口原有图形将不复存在。若希望在已存在的图形上再继续添加新的图形，可以使用图形保持命令hold。

hold on保持

hold off取消保持

hold 在两者之间切换

三、设置曲线样式

调用格式为：

plot(x1,y1,选项1,x2,y2,选项2,……,xn,yn,选项n)

    其中选项的顺序好像没有关系- -，大家可以试一试

四、图形标注与坐标控制

1、图形标注

（因为可以直接加，所以这些命令了解一下就好了。。）

2、坐标控制

（因为也可以直接调整，所以了解一下就好）

（1）调整坐标函数

axis([xmin xmax ymin ymax zmin zmax])

（2）grid命令

    grid on 画网格线

    grid off 不画网格线

    grid      进行切换

五、图形的可视化编辑

（因为2014有官方中文版，所以就不需要多说了- -）

六、对函数自适应采样的绘图函数

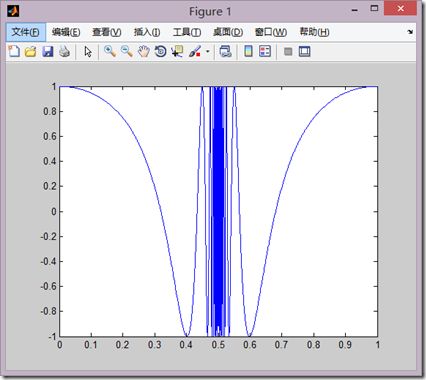
     主要是我们使用plot函数的时候，我们为了方便都是取等步长的点，这样的话，如果遇到疏密不一的曲线就很难描绘出来，所以还有一个函数可以直接进行适应。

1、调用格式

fplot(fname,lims,tol,选项)

其中：fname为函数名，以字符串的形式出现。可以是由多个分量函数构成的行向量，分量函数可以是函数的直接字符串，也可以是内部函数名或函数文件名。

        lims为x,y的取值范围。可以取二元向量，也可以四元向量

        tol为允许的相对误差

2、实例

>> fplot('cos(tan(pi*x))',[0,1],1e-4)

换句话说，我们在绘制已知表达式的情况下，使用这用绘制方法是最好的。

七、图形窗口的分割

       如果我们需要在一个图形窗口内绘制若干个独立的图形，这就需要对图形窗口进行分割。分割后的图形窗口由若干个绘图区组成，每一个绘图区可以建立独立的坐标系并绘制图形。

1、subplot函数的调用格式

subplot(m,n,p)

      作用是将当前图形窗口分成m*n个绘图区，区号是按照行号优先编号，且选定第p个区为当前互动区。

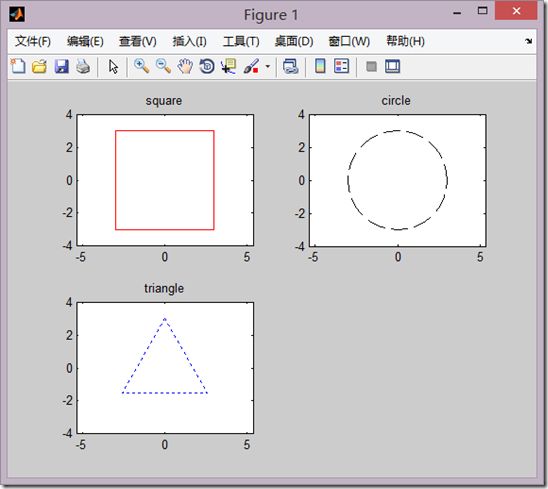
2、一个demo

x_square=[-3,3,3,-3,-3];
y_square=[3,-3,3,3,-3];
x_circle=3*cos((0:10:360)*pi/180);
y_circle=3*sin((0:10:360)*pi/180);
x_triangle=3*cos([90,210,330,90]*pi/180);
y_triangle=3*sin([90,210,330,90]*pi/180);
subplot(2,2,1);
plot(x_square,y_square,'-r');
axis([-4,4,-4,4]);
axis('equal');
title('square');

subplot(2,2,2);
plot(x_circle,y_circle,'--k');
axis([-4,4,-4,4]);
axis('equal');
title('circle');

subplot(2,2,3);
plot(x_triangle,y_triangle,':b');
axis([-4,4,-4,4]);
axis('equal');
title('triangle');

（二）其他二维图形

一、其他坐标系下的二位数据曲线图

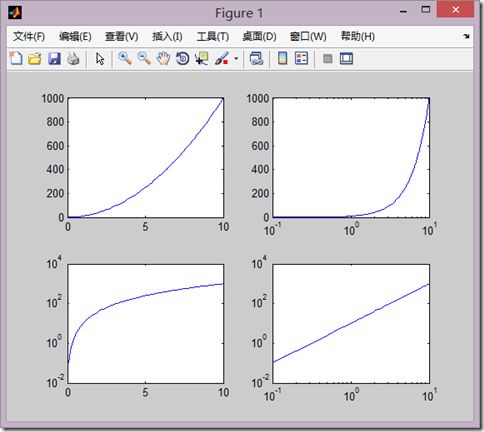
1、对数坐标图形

（1）调用格式

semilogx(x1,y1,选项1,x2,y2,选项2……)
semilogy(x1,y1,选项1,x2,y2,选项2……)
loglog(x1,y1,选项1,x2,y2,选项2……)

      第一个函数为x为对数坐标，y为线性刻度。

      第二个函数为y为对数坐标，x为线性刻度。

      第三个函数x,y都是对数坐标。

（2）demo

x=linspace(0,10,100);
y=10*x.*x;
subplot(2,2,1);
plot(x,y);

subplot(2,2,2);
semilogx(x,y);

subplot(2,2,3);
semilogy(x,y);

subplot(2,2,4);
loglog(x,y);

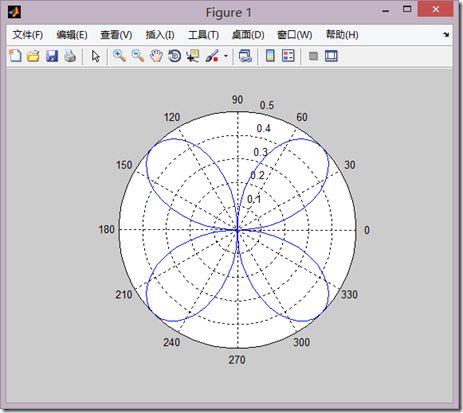
2、极坐标图

（1）调用格式

polar(theta,rho,选项)

      其中theat为极角，rho为矢径

（2）demo

>> r=sin(t).*cos(t);
>> polar(t,r)

二、二维统计分析图

条形图	bar(x,y,选项)
阶梯图	stairs(x,y,选项)
杆图	stem(x,y,选项)
填充图	fill(x1,y1,选项1,x2,y2,选项2……）
饼图	pie([a0,a1,a2,……])

      前三个跟plot类似，然后fill就是将这些点连起来，然后如果最后不是封闭图形，那么首尾会自动连接起来。

（三）隐函数绘图

（四）三维图形

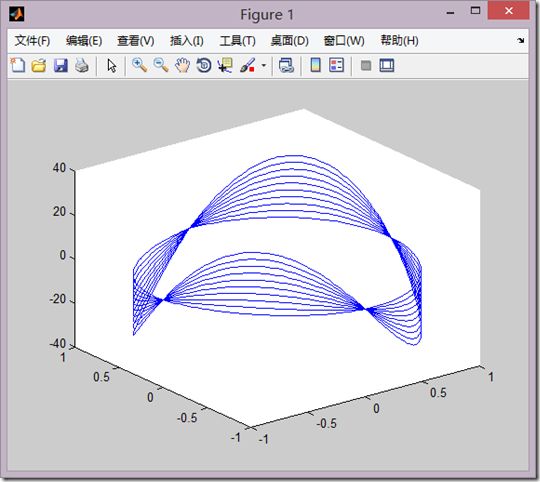
一、三维曲线

1、最基本的三维图形函数plot3

（1）用来绘制三维曲线

（2）格式

plot3(x1,y1,z1,选项1,x2,y2,z2,选项2……)

（3）demo

t=0:pi/100:20*pi;
x=sin(t);
y=cos(t);
z=t.*sin(t).*cos(t);
plot3(x,y,z);
gride on;

二、三维曲面

1、产生三维数据

      绘制z=f(x,y)所表示的三维全面图，先要在x,y平面选定一个矩形区域，分成很多小块，然后确定x和y（中心），然后带入f(x,y)，求Z

（1）在MATLAB中产生网格坐标矩阵

x=a:d1:b;
y=c:d2:d;
[X,Y]=meshgrid(x,y);

      a、X矩阵的每一行都是向量X，行数等于Y元素的个数

      b、Y矩阵的每一列都是向量Y，列数等于X元素的个数

      c、当x=y的时候，可以只调用meshgrid（x)

（2）计算Z

      当然一般z是需要用for循环还有条件语句来构造的。

2、绘制三维曲面的函数

（1）调用格式

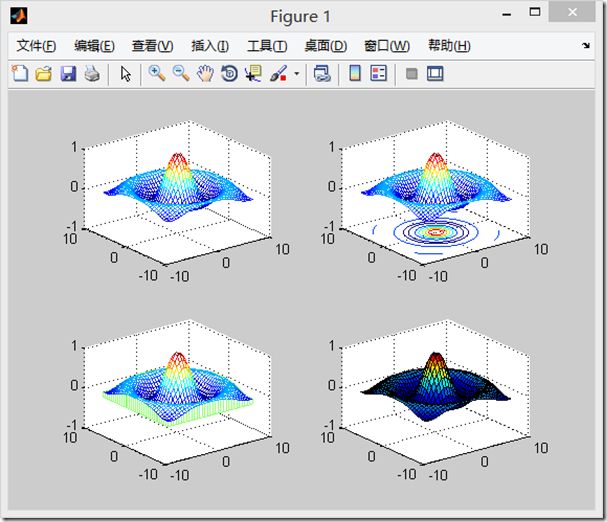
a、mesh(x,y,z,c):用于绘制三维网格图，比较粗糙

    meshc(x,y,z,c):会带有等高线

    meshz(x,y,z,c):会带有曲线的底座

b、surf（x,y,z,c)：用于绘制三维曲面，精细

    ① 其中，x,y,z是同一纬度的矩阵，z=f(x,y)，c用于制定在不同高度下的颜色范围，c省略时，默认c=z。 

    ② 然后如果x,y省略的话，z的列下标作为x轴坐标，z的行下标作为y轴坐标。

    ③ 如果X，y是向量，那么length(x)等于Z的列，length(y)的长度等于Z的行。

（2）一个demo

[x,y]=meshgrid(-8:0.5:8);
z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2);
subplot(2,2,1);
mesh(x,y,z);

subplot(2,2,2);
meshc(x,y,z);

subplot(2,2,3);
meshz(x,y,z);

subplot(2,2,4);
surf(x,y,z);

3、标准三维曲面

（1）shpere(n)

a、调用格式

[x,y,z]=sphere(n);

     该函数将产生(n+1)^2的矩阵x,y,z，采用这三个矩阵绘制出圆心位于原点，半径为1的单位球体，n决定了球面的圆滑程度

（2）cylinder函数

a、调用格式

[x,y,z]=cylinder(R,n)

     其中R是一个向量，存放柱面各个等间隔高度上的半径，n表示在圆柱圆周上有n个间隔点。

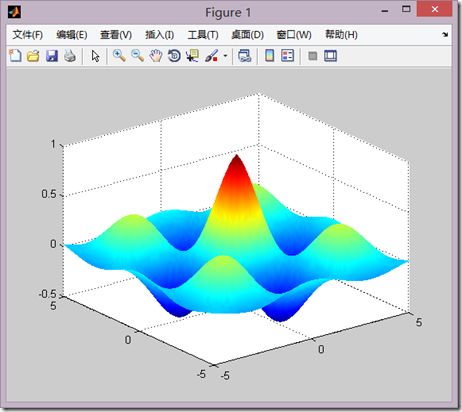
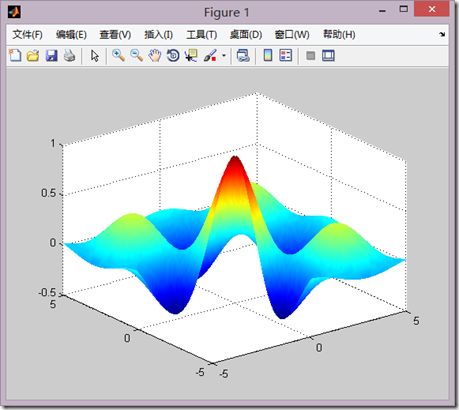
（3）peak函数

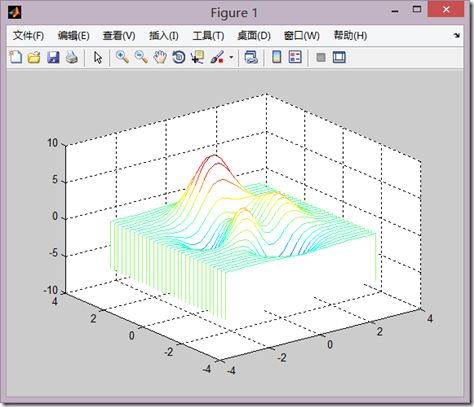
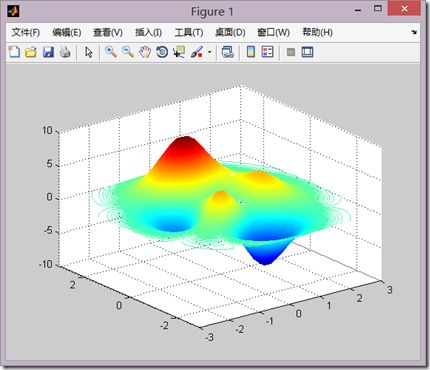
    用来展示三维曲面。z=f(x,y)的函数关系如下

    调用格式

z=peaks(n)

（4）一个demo

t=linspace(0,2*pi,40);

[x,y,z]=cylinder(2+sin(t),30);
subplot(2,2,1);
surf(x,y,z);

subplot(2,2,2);
[x,y,z]=sphere;
surf(x,y,z);

subplot(2,1,2);
[x,y,z]=peaks(30);
surf(x,y,z);

三、其他三维图形

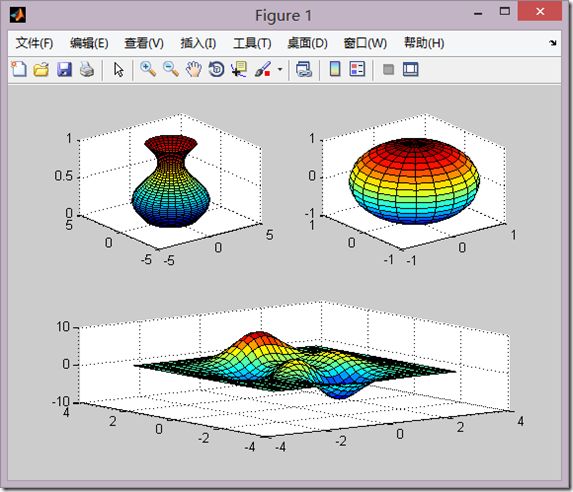
1、绘制统计图

三维条形图	bar3(y)	y的每一个元素对应一个条形
	bar3(x,y)	在x指定的位置上绘制y中元素的条形图
三维杆图	stem3(z)	将数据序列z表示为从xy平面向上延伸的杆图
	stem3(x,y,z)	在指定位置上画杆图
三维饼图	pie3(x)	X为向量，用于绘制一个三维饼图
	fill3（x,y,z,c)	使用x,y,z作为多边形的顶点，c制定了填充的颜色

一个demo

t=linspace(0,2*pi,40);

subplot(2,2,1);
bar3(magic(4));

subplot(2,2,2);
y=2*sin(0:pi/10:2*pi);
stem3(y);

subplot(2,2,3);
pie3([1000,2000,3000,4000]);

subplot(2,2,4);
fill3(rand(3,5),rand(3,5),rand(3,5),'y');

2、瀑布图

     调用格式

waterfall(X,Y,Z)

3、等高线图

>> contour3(X,Y,Z,1000);

   其中1000表示高度的等级数，越大表示分的越精细

（五）图形修饰处理

一、视点处理

     通过修改视点来看到不同角度的形状。

1、函数格式

view(az,el)

      az表示方位角，el表示仰角

2、其实可以直接在选项中直接转动= =，所以不哆嗦

二、色彩处理

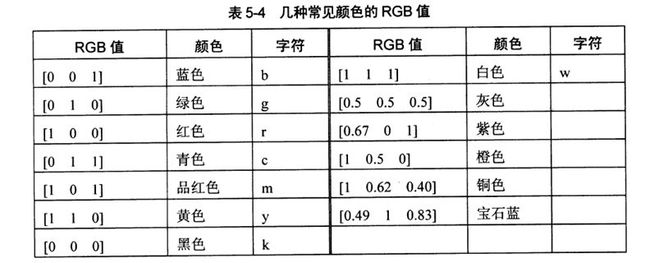
1、颜色的向量表示。

2、色图

      就是一个m*3的数值矩阵，每一行表示一个RGB三元组。色图可以认为生成，也可以调用函数

       除了plot和其派生函数，其他函数均使用色图着色。使用这个函数可以改变色图

colormap(m)

       其中m表示色图矩阵    

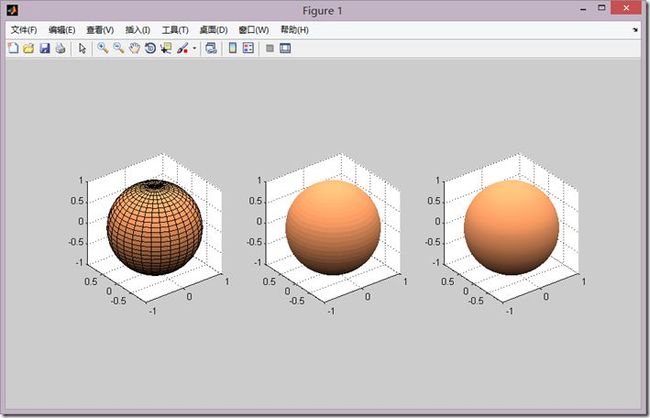
3、三维表面图形的着色

一个demo

[x,y,z]=sphere(30);

colormap(copper);

subplot(1,3,1);
surf(x,y,z);
axis equal;

subplot(1,3,2);
surf(x,y,z);
shading flat;
axis equal;

subplot(1,3,3);
surf(x,y,z);
shading interp;
axis equal;

三、光照处理

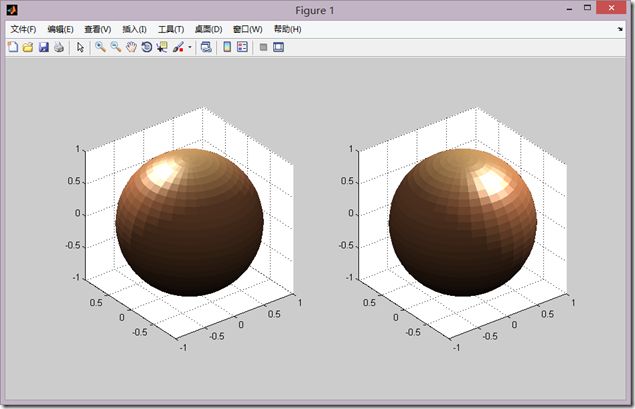
light('color;,选项1，'style',选项2，'position',选项3）

      选项1表示颜色 ，

      选项2：’infinite’表示无穷远光，’local’表示近光、

      选项3：表示光照来的位置

[x,y,z]=sphere(30);


subplot(1,2,1);
surf(x,y,z);
axis equal;
shading flat;
light('posi',[0,1,1]);


subplot(1,2,2);
surf(x,y,z);
shading flat;
axis equal;
light('posi',[1,0,1]);

四、图形的裁剪处理

[x,y]=meshgrid(-5:0.1:5);
z=cos(x).*cos(y).*exp(-sqrt(x.^2+y.^2)/4);
surf(x,y,z);
shading interp;
pause;

i=find(x<=0&y<=0);
zi=z;
zi(i)=NaN;
surf(x,y,zi);
shading interp;

（六）图像处理与动画制作