C++数据结构之最小生成树
最小生成树是图的一部分,一般求最小生成树用Prim算法和Kruskal算法。
对于Prim算法,思想是:在访问过的顶点和未访问的顶点之间选择权值最小的边。Prim算法是基于顶点的操作,适合于顶点较少,边较多的图。
对于Kruskal算法,思想是:直接从图中选择权值最小的边,并且已选择的边不能构成连通图。Kruskal算法是基于边的操作,适合于边较少,顶点较多的图。
Prim算法,在此我用了关联容器pair作为边的存储结构:
//普里姆算法
int Prim(const int G[][VNUM], vector<pair<int, int> > &edge)
{
int w = 0; //权重
vector<int> visited(VNUM, 0); //已访问节点集合
//初始化
visited[0] = 1; //0号节点已访问
//循环VNUM-1次
int u, v;
for(int number = 1; number < VNUM; ++number)
{
int min = M;
for(int i = 0; i != VNUM; ++i) //一次循环有一个节点入栈
{
if(visited[i] == 1)
{
for(int j = 1; j != VNUM; ++j) //判断边(i, j)的权值,i为已访问节点,j为未访问节点
{
if(visited[j] == 0 && G[i][j] < min)
{
min = G[i][j];
v = i;
u = j;
}
}
}
}
w += G[v][u];
visited[u] = 1;
edge[number-1].first = v;
edge[number-1].second = u;
}
return w;
}
克鲁斯卡尔算法的最小生成树结构用并查集表示,并查集在次主要用来判断已选择的边是否构成连通图,如果对应顶点x,y的FindRoot()操作返回的结果相同,即他们的根相同,则能够成连通图,说明选择的边不满足条件。
//并查集结构
class DisjointSet{
public:
vector<int> father;
DisjointSet(int VNUM){
father.resize(VNUM, -1);
}
int FindRoot(int x)
{
while(father[x] >= 0)
x = father[x];
return x;
}
void Union(int x, int y)
{
father[FindRoot(x)] = FindRoot(y);
}
};
//Kruskal
int Kruskal(const int G[][VNUM], vector<pair<int, int> > &edge)
{
int min = M;
int w = 0;
int v, u;
DisjointSet V(VNUM);
for(int num = 0; num != VNUM-1; ++num)
{
min = M;
for(int i = 0; i != VNUM; ++i)
{
for(int j = 0; j != VNUM; ++j)
{
if(G[i][j] < min && V.FindRoot(i) != V.FindRoot(j))
{
min = G[i][j];
v = i;
u = j;
}
}
}
w += G[u][v];
V.Union(u, v);
edge[num].first = v;
edge[num].second = u;
}
return w;
}
下面是主程序:
/*************************
Date : 2013-9-20
Author : DVD0423
Function: 无向图的最小生成树
******************&******/
#include <iostream>
#include <vector>
#include <utility>
using namespace std;
const int M = 10; //两节点无边权值用M表示
const int VNUM = 6;
int Prim(const int G[][VNUM], vector<pair<int, int> > &edge);
int Kruskal(const int G[][VNUM], vector<pair<int, int> > &edge);
int main()
{
const int G[VNUM][VNUM] = {
M, 9, 1, M, 7, 2,
9, M, 5, 1, M, 6,
1, 5, M, 4, 2, 6,
M, 1, 4, M, 9, 3,
7, M, 2, 9, M, M,
2, 6, 6, 3, M, M
};
vector<pair<int, int> > edge(VNUM-1);
//Prim
cout<<"普里姆算法:"<<endl;
cout<<"总路径长度:"<<Prim(G, edge)<<endl;
for(int i = 0; i != VNUM-1; ++i)
cout<<"("<<edge[i].first<<", "<<edge[i].second<<")"<<endl;
//Kruskal
cout<<"克鲁斯卡尔算法:"<<endl;
cout<<"总路径长度:"<<Kruskal(G, edge)<<endl;
for(int i = 0; i != VNUM-1; ++i)
cout<<"("<<edge[i].first<<", "<<edge[i].second<<")"<<endl;
return 0;
}
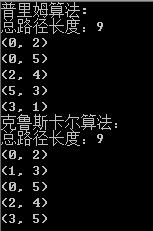
输出结果如下: